基于雙層相空間相似度的滾動軸承故障模式與故障程度的綜合辨識

劉永斌， 何 兵， 劉 方， 趙藝雷， 方 健

(1.安徽大學 機械工程系,合肥 230601；2.中國科學技術大學 精密機械與精密儀器系,合肥 230027)

基于雙層相空間相似度的滾動軸承故障模式與故障程度的綜合辨識

劉永斌1,2， 何 兵1， 劉 方1， 趙藝雷1， 方 健1

(1.安徽大學 機械工程系,合肥 230601；2.中國科學技術大學 精密機械與精密儀器系,合肥 230027)

提出了一種基于雙層相空間相似度分析算法結構，應用于滾動軸承故障類型和故障程度的綜合辨識。該算法第一層結構中，對測試數據和樣本數據進行相空間重構(PSR)，得到在拓撲意義下等價的相空間，然后使用滑動窗截取數據段，采用歸一化互相關函數(NCC)進行相空間相似度分析，實現軸承故障類型的分類；在第二層結構中，以已知不同故障程度數據之間的相空間相似度(PSS)為特征訓練SVR結構，實現對故障程度的跟蹤。實驗信號分析結果表明，該方法能有效對軸承故障類型和故障程度進行綜合辨識。與傳統方法的對比表明該方法在準確性上有了一定的提高。

滾動軸承；故障診斷；相空間重構；相似度分析

由于實際工況的復雜性，滾動軸承故障信號通常含有較強的背景噪聲，并且經常表現出較強的非線性和非平穩性[1]。如何從檢測信號中提煉表征故障狀態的特征，對軸承故障進行辨識成為診斷的難點之一。常用的特征提取方法有時域模型分析、頻域模型分析以及Hilbert-Huang變換分析、小波分析等時頻域模型分析[2-5]。而當采用的特征參數過多又會使計算過于復雜，甚至影響分類精度[6]。因此降維技術被用于故障診斷，主分量分析(Principal Component Analysis，PCA)可以通過線性變換實現原始特征降維,再通過機器學習方法而實現對故障模式的辨識[7]。而實際上，振動源的振動特性滿足高斯分布的情況很少，此種情況下，獨立分量分析(Independent Component Analysis，ICA)更能反映出數據的高階統計結構[8]。

混沌時間序列分析作為研究非線性信號的一種新方法，可以很好把握原序列的性質與規律，鑒于此，本文提出了基于雙層相空間相似度分析的滾動軸承故障類型與故障程度的綜合辨識。其首要的一步即重構相空間，本文中采用的是坐標延遲相空間重構法。首先對樣本數據和滑動窗截取后的測試數據進行相空間重構，然后采用歸一化互相關函數(Normalized Cross Correlation，NCC)求兩者之間的相空間相似度(Phase Space Similarity，PSS)。在本文所提出的雙層結構中，第一層通過比對當前數據與各種故障模式數據的PSS，通過模板匹配確定當前數據的故障模式；在第二層中，利用不同故障程度之間的PSS作為訓練樣本來訓練支持向量回歸機(Support Vector Regression，SVR)的結構，從而實現對當前故障程度的預測。

相空間能夠表征不同的軸承健康狀態下的監測序列信號之間的內在聯系，通過實驗數據的分析，表明此方法能夠很好的實現對滾動軸承故障類型與故障程度的綜合辨識，并且與其它方法進行對比，發現此方法在判別準確度上有了一定的提高。

1 基本理論

1.1 相空間重構

關于在混沌時間序列中重構相空間開始于PACKARD等[9],提出了兩種相空間重構方法，即導數重構法和坐標延遲重構法。在實際運用中，混沌時間序列的先驗信息難以獲得，所以一般采用坐標延時重構法[10]。該方法的本質是把一個非線性時間序列通過不同的時間延遲來構造一個高維的相空間。假設原始時間序列為x=(x1,x2,…,xn)，構造的d維相空間矢量為

Xi(d)=[xi,xi+τ,...,xi+(d-2)τ,xi+(d-1)τ]

(1)

式中:n為時間序列的點數;d為嵌入維數;τ為時間延遲。根據Takens定理,對于理想的無限長和無噪聲的時間序列，嵌入維數d和時間延遲τ可以取任意值，但實際信號都不能滿足此類條件，所以必須通過計算得到最合適的d和τ值，否則會影響重構的相空間的質量[11]。

如果時間延遲τ取值過小，則相空間矢量(1)中兩個相鄰的分量在數值上會非常相似，導致區分的效果不明顯；反之，如果取值過大，兩個分量在統計意義上是獨立的。本文采用自相關函數法對τ進行確定，其定義為

(2)

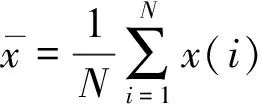
混沌時間序列中選擇最小嵌入維數共有以下幾種：飽和關聯維數(G-P)法、偽鄰近點法[13]和CAO[14]方法。其中CAO方法對數據量要求不高，容易區分隨機序列與確定時間序列。所以在本文中，采用CAO算法來確定嵌入維數，假設嵌入維數為d，則按照式(1)的形式，此相空間的第i個點為Xi(d)，與它最近的一個點是Xn(i,d)(d),根據嵌入定理，兩點在d維的相空間下最近，那么在d+1維下的相空間也是最近的。

(3)

(4)

(5)

當在d維和d+1維的相空間在拓撲意義下相等時，隨著d的增大，E1(d)逐漸趨于穩定，所以嵌入維數就是使E1(d)穩定的最小d值。而在實際工況中，由于采樣數據有限，很難判斷E1(d)是否穩定，需要一個補充標準進行共同判斷。

(6)

(7)

如果時間序列是隨機信號，則E2(d)=1，如果時間序列為確定信號，則E2(d)將隨著d的變化而變化。所以通過觀察E2(d)隨d的變化曲線可以得到觀察信號是否為確定信號。而E1(d)隨d的增長會逐漸趨于穩定，則嵌入維數就是使E1(d)穩定的最小d值。

1.2 歸一化互相關

經典的相關匹配方法有：基于最多鄰近點距離(Maximum Close Distance,MCD)、二維最小絕對差累加和算法(Minimum Absolute Difference,MAD)、歸一化互相關(NCC)[15]。其中NCC匹配算法常用于圖像匹配中，用來定位圖像中的一個位置，通過計算模板和待匹配圖像的互相關值，互相關值最大時所對應的搜索窗口決定了某種圖像在待匹配圖像中的位置。與其他相關匹配方法相比，此方法對噪聲的魯棒性較好，匹配精度高[16]。假設已知的樣本相空間為Z={Z1,Z2,…,Zm}，當前相空間為Y={Y1,Y2,…,Ym},m是相點的個數，則Y與Z的相空間相似度為

(8)

1.3 支持向量回歸建模

SVR是基于支持向量機(Support Vector Machine, SVM)在回歸學習中的一種應用，可實現對時間序列的預測。支持向量機是VAPNIK等[17]提出的一個有限樣本的機器學習方法，由線性可分情況下的最優分類面發展而來，如圖1所示，其中圓和叉號分別代表兩類數據，H為分類線，H1、H2分別為兩類中距離分類線最近并且平行于分類線的直線，直線上的點叫做支持向量，它們之間的距離就是分類間隔。

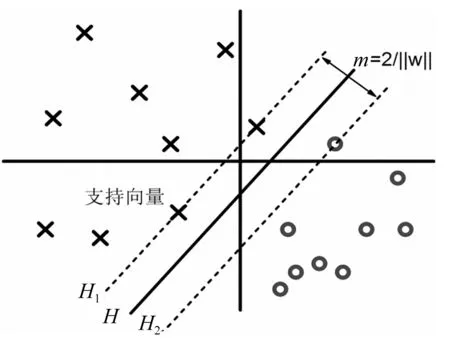
圖1 支持向量機原理圖Fig.1 The principle diagram of the support vector machine

對于SVR，用線性回歸函數f(x)=w·x+b,擬合數據{xi,yi},i=1,2,…,n,其中xi是輸入特征，yi是實驗現象。假設在精度ε下所有的訓練數據可以無誤差的用線性函數擬合[18],即

(9)

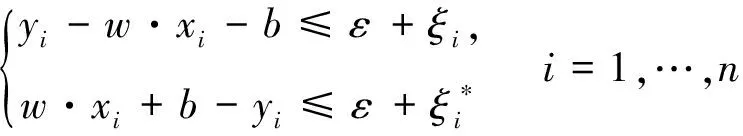
(10)

式中,C>0，C是對超出誤差ε的樣本懲罰程度，這是一個凸二次規劃問題，引入Lagrange函數

(11)

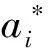
(12)

得到的回歸函數為

f(x)=(w·x)+b=

(13)

2 方法步驟

為了獲取動態系統的定性信息，往往需要知道充分的狀態演化信息，但在實際情況中，數據采集設備只能得到反映系統信息的一維向量，即時間序列。雖然采集到的軸承振動信號在一維下具有不同的振動趨勢，但不能充分的反映系統的狀態。因此本文提出通過相空間重構得到系統在某個狀態下的特性,并通過NCC得到PSS，其框圖如圖2所示。

在時間序列重構中，通過運用相空間重構把一維的時間序列嵌入成高維相空間。假設第j個時間序列為xj=(x1j,x2j,…,xnj)，n為時間序列xj中的采樣個數，采用自相關函數法確定時間延遲τ。然后采用CAO算法確定最小嵌入維數dj，為了簡化不同時間序列有不同的最小嵌入維數，這里統一了嵌入維數為d，其中d>dj。得到重構后的相空間為

(14)

Yk=[yi,yi+τ,…,yC-dτ]T

(15)

2.1 基于相空間相似度的滾動軸承故障模式識別

在第一層結構中，以各種故障模式的振動數據為數據庫，以提取的PSS為特征進行模板匹配，從而確定當前數據的故障模式(見圖3)。

圖2 相空間相似度提取過程Fig.2 The feature extraction of phase space similarity

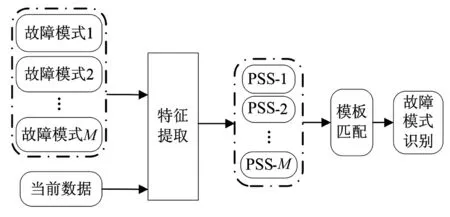
圖3 第一層結構框圖Fig.3 Framework of the first layer structure

2.2 基于相空間相似度和SVR的軸承故障程度識別

在第一層中通過相空間相似度分析，得出了當前數據屬于何種故障模式，而這種故障模式下的數據是屬于何種故障程度仍然不可知，因此提出第二層算法對軸承故障程度進行預測。其流程圖如圖4所示。

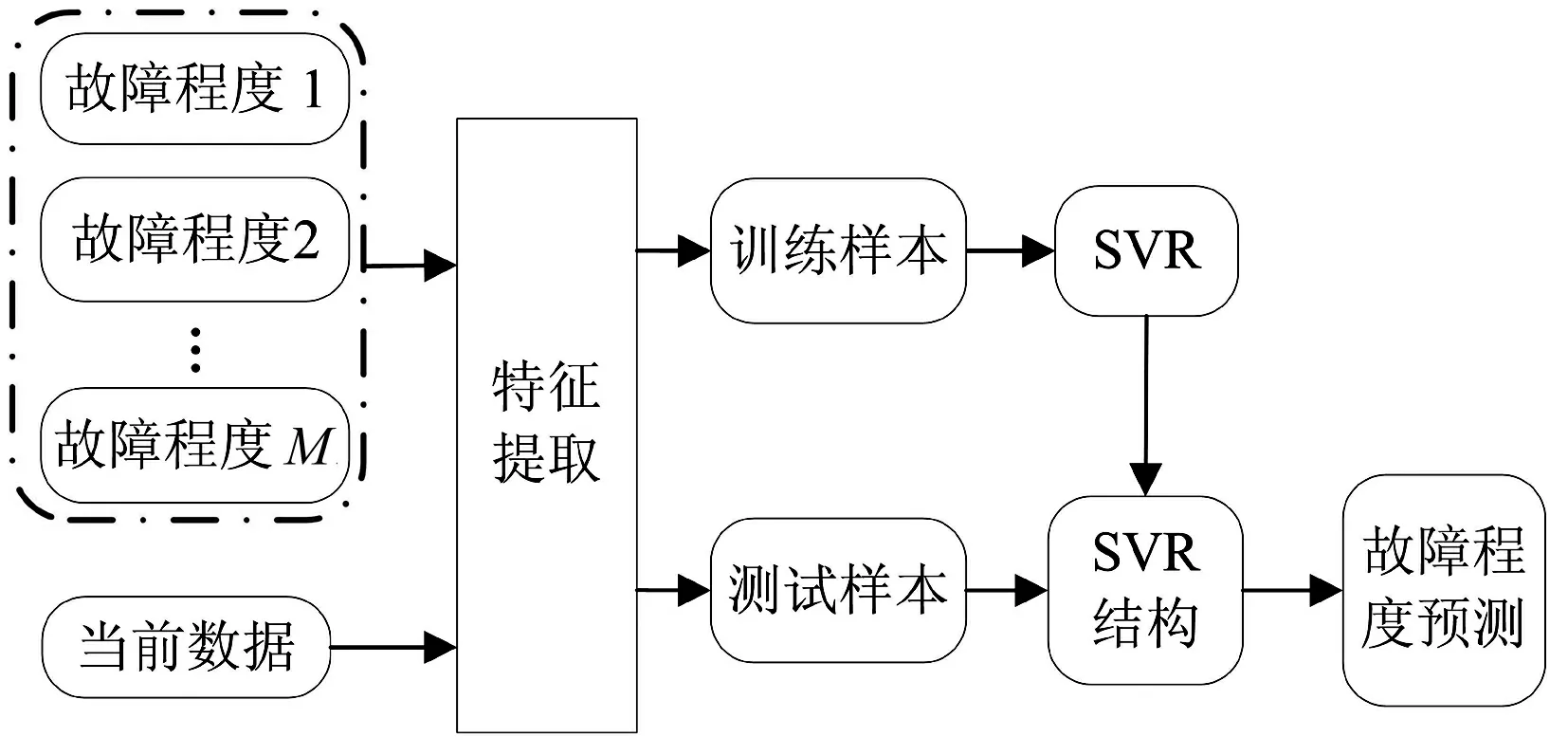
圖4 第二層結構框圖Fig.4 Framework of the second layer structure

在特征提取后產生了訓練樣本和測試樣本，其中訓練樣本為同種故障模式下的已知故障程度的相空間之間的相似度，測試樣本為當前相空間和各故障程度的相空間之間的相似度。利用訓練樣本來訓練各個故障模式下的SVR結構，再把測試樣本輸入到此SVR中，得到所當前數據的故障程度。

3 實驗驗證

為了確認此方法的有效性，采用了Case Western Reserve University電氣工程實驗室的滾動軸承故障模擬試驗臺采集的軸承數據，其試驗平臺如圖5所示，從左至右分別為2馬力的電動機、扭矩傳感器、功率計，被測試的軸承利用電蝕分別在內圈、外圈以及滾動體上設置不同損傷程度的單點故障，然后固定在電動機的軸上進行測試。

圖5 實驗操作平臺Fig.5 The experimental operation platform

其中驅動端的滾動軸承的型號為SKF6205，在電機負載為0時的電機轉速大約為1 797 r/min，采樣頻率為12 kHz。實驗得到1種正常數據和3種故障模式數據。每種故障模式下都包含三種不同故障程度的損傷，損傷斑點直徑分別為0.017 78 cm、0.035 56 cm和0.053 34 cm。對每種數據取30組樣本數據和30組測試數據進行算法有效性驗證，如表1所示。

首先進行故障類型的辨識，利用圖3所示的第一層結構進行處理。通過歸一化自相關函數求出Ci(τ)和時間延遲τ之間的曲線關系，這里以內圈故障且損傷直徑為0.017 78 cm所對應的測試數據為例，其曲線如圖6所示。

表1 軸承數據描述

圖6 Ci(τ)變化曲線Fig.6 The change curve of Ci(τ)

根據圖6所示，可以看出當τ為2的時候，Ci(τ)的值第一次下降到1-1/e，所以得到最合適的時間延遲值為2。然后采用CAO算法對嵌入維數進行確定，得到E1(d)和E2(d)關于維數d的變化曲線如圖7所示。

圖7 E1(d)和E2(d)的變化曲線Fig.7 The change curve of E1(d) and E2(d)

由圖7可知，當d>8時，E1(d)逐漸趨于穩定，并且E2(d)隨著d的變化而變化。當用其他數據做測試的時候，得到的結果和上述結果一樣，所以把嵌入維數設為8。

然后對樣本數據進行相空間重構，而測試數據則先用滑動窗截取，然后對每個片段進行相空間重構，最后利用歸一化互相關函數求出這個當前數據同每個樣本數據之間的最大的相似度。分析過程中，滑動窗口的長度設置為64，每次滑動的步長設置為16。這里以內圈故障且損傷直徑為0.035 56 cm所對應的數據做示例分析，得到測試數據和300個樣本數據的最大相似度，如圖8所示。

圖8 當前數據和各個樣本數據的最大相似度Fig.8 The maximum similarity between current data and the sample data

可以看出當前數據與第61～90的樣本數據的相似度普遍較其他區間的要高，而第61～90的樣本數據屬于內圈故障所對應的數據，所以可以判斷當前數據的故障模式為內圈故障。然后把所有的測試數據依次進行處理，得到的故障類型識別結果如表2所示。

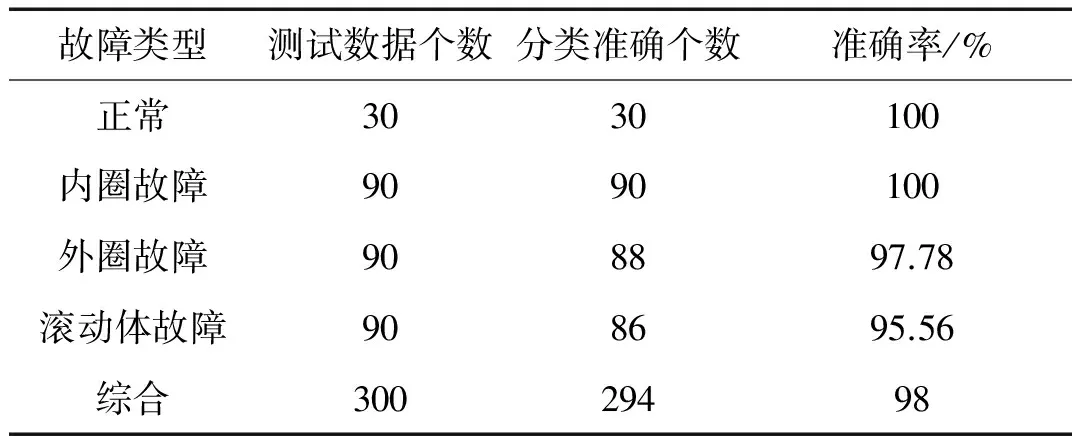
表2 滾動軸承故障類型識別結果

從表2中知，出利用已有的三種故障模式和軸承正常數據可以實現對軸承的故障模式分類，表明基于相空間相似度的滾動軸承的故障模式識別準確性很高，且判斷錯誤大都在滾動體故障的判斷上，通過對各種軸承故障類型的分形維數的分析[19]和計算，其分形維數計算結果如表3所示。得知這是因為有缺陷的滾動體的振動信號更為復雜，隨機性較強。

表3 滾動軸承各故障類型分形維數

在通過第一層的故障模式判斷后，在第二層中以樣本數據在同一個故障模式下的三種故障程度之間的相空間相似度作為特征指標訓練SVR結構，然后以當前測試數據和三種故障程度之間的相空間相似度作為SVR結構輸入，來推測當前測試數據的故障程度，結果如圖9～圖11所示。可見本文方法能有效實現對軸承故障程度的預測。

圖9 內圈故障Fig.9 Inner race fault

圖10 外圈故障Fig.10 Outer race fault

圖11 滾動體故障Fig.11 Roller fault

4 對比分析

為了進一步驗證本文所提出的方法的有效性，本小節將與其他方法進行對比分析，包括與基于原信號相似度的故障類型識別和采用傳統特征提取算法的SVR預測方法的對比。使用原信號做分類時，其識別結果如表4所示。

表4 基于原信號相似度的故障模式識別結果

在故障程度預測對比中，首先是對原始數據進行特征提取，本文一共提取了12種特征值，其中在時域特征有7組；在頻域特征有5組。其中每種故障數據均分為60組，30組用來訓練，30組用來測試。 其結果如圖12～圖14所示。

圖12 傳統SVR內圈故障Fig.12 Inner race fault prediction by traditional SVR

圖13 傳統SVR外圈故障Fig.13 Outer race fault prediction by traditional SVR

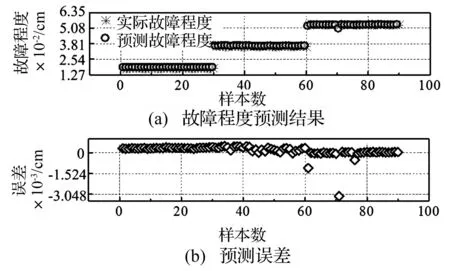
圖14 傳統SVR滾動體故障Fig.14 Roller race fault prediction by traditional SVR

表5 最大預測誤差比較

根據上述圖表所示，經過相空間重構后再進行相似度匹配比原信號直接進行相似度匹配在故障模式的分類準確度上有了一定的提高，說明經過相空間重構后可以更好把握原序列的性質與規律，更能體現各種軸承故障的特征；然后通過和圖12～14和表5的比較，得出本文所提出的方法較傳統特征提取的SVR方法在故障程度識別準確率上有了很大的提高。

5 結 論

本文采用PSR和NCC相結合的方法提取相空間相似度PSS，并通過模板匹配方法實現對故障模式的識別和通過SVR實現對軸承故障程度的預測。通過本文的研究和驗證，可得出以下結論：

(1)針對滾動軸承故障信號的非平穩性和非線性，相空間重構可以更好把握原序列的性質與規律，通過和原信號的分類結果相比，運用相空間重構算法進行分類具有更高的準確性。

(2)本文通過對重構后的信號進行相似度分析來進行分類，并達到了很好的效果，表明相似度分析可以用于故障辨識。

(3)通過驗證，本文所提出的方法可以同時實現對故障類型和故障程度的綜合辨識，和傳統的只對故障模式進行辨識的方法相比，本文所提出的方法功能更加全面，對確定旋轉機械的維修時間有一定的幫助。

(4)通過與原信號以及傳統SVR預測算法相比，本文所提出的算法在實現分類和預測的準確度上更高。

[ 1 ] 何正嘉，訾艷陽，孟慶豐. 機械設備非平穩信號的故障診斷原理及應用[M]. 北京：高等教育出版社,2001.

[ 2 ] 何清波. 多元統計分析在設備狀態監測診斷中的應用研究[D]. 合肥：中國科學技術大學，2007.

[ 3 ] YANG Yu, YU Denjie, CHENG Junsheng. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM [J].Measurement, 2007,40(9/10): 943-950.

[ 4 ] 孔凡讓，朱忠奎，羊拯民，等. 齒輪振動信號特征的小波包頻率表示法[J]. 振動、測試與診斷，2004,24(2)：103-105. KONG Fanrang, ZHU Zhongkui, YANG Zhengmin, et al. The wavelet packet frequency representation of Gear vibration signalcharacteristics[J]. Journal of Vibration, Measurement & Diagnosis,2004,24(2):103-105.

[ 5 ] HE Q. Vibration signal classification by wavelet packet energy flow manifold learning [J]. Journal of Sound and Vibration, 2013, 332(7):1881-1894.

[ 6 ] 劉永斌. 基于非線性信號分析的滾動軸承狀態監測診斷研究[D]. 合肥：中國科學技術大學,2011.

[ 7 ] 劉永斌，何清波，孔凡讓，等. 基于PCA和SVM的內燃機故障診斷[J]. 振動、測試與診斷，2012,32(2)：250-255. LIU Yongbin, HE Qingbo, KONG Fanrang, et al. The internal combustion engine fault diagnosis based on PCA and SVM[J]. Journal of Vibration, Measurement &Diagnosis,2012,32(2):250-255.

[ 8 ] 朱忠奎，陳祥芹，樊薇，等. 基于降維的獨立分量分析及信號特征成分監測[J]. 儀器儀表學報，2014,35(4):917-923. ZHU Zhongkui, CHEN Xiangqing, FAN Wei, et al. Independent component analysis based on dimensionality reduction and its application in signal feature detection[J]. Chinese Journal of Scientific Instrument, 2014, 35(4):917-923.

[ 9 ] PACKARD N H, CRUTCHFIELD J P, FARMER J D, et al. Geometry from a time series[J]. Physical Review Letters, 1980, 43(9):712-715.

[10] 陳鏗，韓伯棠. 混沌時間序列分析中的相空間重構技術綜述[J]. 計算機科學，2005,32(4):67-70. CHEN Keng, HAN Botang. A survey of state space reconsition of chaotic time serious analysis[J]. Chinese Journal of Computer,2005,32(4):67-70.

[11] 孫雅明，張智晟．相空間重構和混沌神經網絡融合的短期負荷預測研究[J]．中國電機工程學報,2004, 24(1)：44-48． SUN Yaming，ZHANG Zhisheng．A new model of STLF based on the fusion of PSRT and chaotic neural networks[J]．Proceedings of the CSEE，2004，24(1):44-48．

[12] ROSENSTEIN M T, COLLINS J J, LUCA C J D. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D Nonlinear Phenomena,1993,65(1/2):117-134.

[13] KERMEL M B, BROWN R, ABARBANEL H D I. Detennining embedding dimension for phase-space reconstruction using a geometrical reconstruction [J].Physical Review A,1992,45(6):3403-3410.

[14] CAO L Y. Practical method for determining the minimum embedding dimension of a scalar time series [J]. Physica D Nonlinear Phenomena, 1997,110(1/2):43-50.

[15] BROWN L G. A survey of image registration techniques[J]. ACM Computing Surveys, 1992,24(4): 325-376.

[16] TSAI D M, LIN C T. Fast normalized cross correlation for defect detection [J]. Pattern Recognition Letter, 2003,24(15):2625-2631.

[17] VAPNIK V N. The nature of statistical learning theory [M]. New York: Spring-Verlag,1995.

[18] 沈長青，朱忠奎，黃偉國，等. 基于支持向量回歸方法的齒輪箱故障診斷研究[J].振動、測試與診斷，2013,33(5)：775-781. SHEN Changqing, ZHU Zhongkui, HUANG Weiguo, et al. Gear box fault diagnosis based on support vector regression method[J].Journal of Vibration, Measurement &Diagnosis,2013,33(5):775-781.

[19] 胥永剛，何正嘉. 分形維數和近似熵用于度量信號復雜性的比較研究[J].振動與沖擊，2003，22(3):25-27. XU Yonggang, HE Zhengjia. Research on comparison between approximate entropy andfractal dimension for complexity of signals [J]. Journal of Vibration and Shock, 2003,22(3):25-27.

Comprehensive recognition of rolling bearing fault pattern and fault degrees based on two-layer similarity in phase space

LIUYongbin1,2,HEBing1,LIUFang1,ZHAOYilei1,FANGJian1

(1. Department of Mechanical Engineering, Anhui University, Hefei 230601, China； 2. Department of Precision Machinery and Precision Instrumentation, University of Science and Technology of China, Hefei 230027, China)

A comprehensive method for rolling bearing fault patterns and fault degree recognition based on two-layer algorithm structure of phase space similarity analysis was presented in this paper. In the first layer of the algorithm, the data were processed by the phase space reconstruction (PSR) to get a phase space which was equivalence in the topological sense. Then a sliding window was employed to chop the data segments and the normalized cross correlation function (NCC) was employed to execute similarity analysis, realizing the classification of bearing fault patterns. In the second layer, a SVR structure was trained by phase space similarity (PSS) that was obtained in different fault degree. The SVR structure was then used to recognize the fault degree. The results of experimental signal analysis show that the proposed method can effectively recognize comprehensive bearing fault pattern and fault degree. Compared with traditional methods, it shows an improvement in accuracy of recognition.

rolling bearing; fault diagnosis; phase space reconstruction; similarity analysis

國家自然科學基金資助項目(51505001)；安徽省教育廳基金資助重點項目(KJ2013A010)；安徽省自然科學基金(1508085SQE212)

2015-06-23 修改稿收到日期：2015-12-25

劉永斌 男，博士，副教授，1971年生

劉方 男，博士，講師，1987年生

TH133.3;TH113.1

A

10.13465/j.cnki.jvs.2017.04.028