非穩(wěn)態(tài)雷暴沖擊風(fēng)場(chǎng)的瞬態(tài)數(shù)值模擬

汪之松， 王 超， 劉亞南， 李正良

(1.重慶大學(xué) 土木工程學(xué)院，重慶 400045; 2.重慶大學(xué) 山地城鎮(zhèn)建設(shè)與新技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，重慶 400045;3.湖南省建筑設(shè)計(jì)院，長(zhǎng)沙 410001)

非穩(wěn)態(tài)雷暴沖擊風(fēng)場(chǎng)的瞬態(tài)數(shù)值模擬

汪之松1,2， 王 超3， 劉亞南1， 李正良1,2

(1.重慶大學(xué) 土木工程學(xué)院，重慶 400045; 2.重慶大學(xué) 山地城鎮(zhèn)建設(shè)與新技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，重慶 400045;3.湖南省建筑設(shè)計(jì)院，長(zhǎng)沙 410001)

沖擊射流是雷暴沖擊風(fēng)場(chǎng)研究中最常用的模擬方法。大部分物理試驗(yàn)和數(shù)值模擬都是假定射流速度入口風(fēng)速不隨時(shí)間變化，而實(shí)際雷暴沖擊風(fēng)的下沉氣流速度都是隨時(shí)間連續(xù)變化的。在雷暴沖擊風(fēng)的全生命周期內(nèi)一般會(huì)經(jīng)歷逐漸增大到最大值后再逐漸減小的過(guò)程。對(duì)于重要的工程結(jié)構(gòu)抗風(fēng)設(shè)計(jì)而言，得到雷暴沖擊風(fēng)全生命周期的風(fēng)速時(shí)程信息十分有必要。基于沖擊射流三維足尺模型模擬雷暴沖擊風(fēng)風(fēng)場(chǎng)，在入口處引入一個(gè)更符合雷暴沖擊風(fēng)實(shí)際演化過(guò)程的衰減函數(shù)，采用大渦模擬數(shù)值分析獲得了雷暴沖擊風(fēng)的非穩(wěn)態(tài)風(fēng)場(chǎng)，并得到其隨時(shí)間衰減的瞬態(tài)演化過(guò)程。結(jié)果表明，該模擬方法可以較好地再現(xiàn)雷暴沖擊風(fēng)場(chǎng)的非穩(wěn)態(tài)過(guò)程，為進(jìn)一步討論非穩(wěn)態(tài)雷暴沖擊風(fēng)場(chǎng)中的結(jié)構(gòu)風(fēng)荷載特性奠定了基礎(chǔ)。

雷暴沖擊風(fēng)；非穩(wěn)態(tài)；沖擊射流；大渦模擬；數(shù)值模擬

雷暴沖擊風(fēng)下沉氣流沖擊地面后，其水平風(fēng)速在近地面區(qū)域產(chǎn)生劇烈的低空風(fēng)切變，對(duì)建筑物和輸電塔等結(jié)構(gòu)有強(qiáng)烈的破壞作用。近年在國(guó)內(nèi)發(fā)生了大量的輸電線塔風(fēng)致倒塌事故，有記錄的75起輸電線塔災(zāi)害事故中絕大多數(shù)都是由雷暴天氣產(chǎn)生的雷暴沖擊風(fēng)造成[1-2]。國(guó)內(nèi)外眾多學(xué)者已采用實(shí)際觀測(cè)、理論研究、物理實(shí)驗(yàn)和數(shù)值模擬等方法對(duì)雷暴沖擊風(fēng)進(jìn)行了研究，并有一些學(xué)者提出了沖擊風(fēng)徑向和豎向風(fēng)剖面的解析、經(jīng)驗(yàn)?zāi)Ｐ蚚3-6]，研究重點(diǎn)從最早的集中于實(shí)測(cè)記錄和數(shù)據(jù)收集，到后來(lái)的穩(wěn)態(tài)和瞬態(tài)的沖擊風(fēng)理論研究和實(shí)驗(yàn)、數(shù)值模擬。SHEHATA[7]研究了一個(gè)跨度為480 m的輸電線路沖擊風(fēng)荷載，得出沖擊風(fēng)的整個(gè)生命周期和強(qiáng)度衰減是非常重要的參數(shù)。ABD-ELAAL[8]基于數(shù)值模擬研對(duì)非穩(wěn)態(tài)雷暴沖擊風(fēng)的影響因素進(jìn)行參數(shù)分析，表明獲取雷暴沖擊風(fēng)的非穩(wěn)態(tài)特性及其整個(gè)生命周期和強(qiáng)度衰減的信息十分必要。

關(guān)于沖擊風(fēng)的非穩(wěn)態(tài)研究，F(xiàn)UJITA[9]記載了發(fā)生于1983年7月1日美國(guó)華盛頓圣安德魯斯空軍基地(AAFB)的一次強(qiáng)烈的沖擊風(fēng)風(fēng)速時(shí)程表現(xiàn)出強(qiáng)烈的非平穩(wěn)特性。HJELMFELT[10]總結(jié)了(Joint Airport Weather Studies,JAWS)研究的數(shù)次沖擊風(fēng)記錄與出流強(qiáng)度隨時(shí)間變化情況，表明沖擊風(fēng)從開(kāi)始到最大強(qiáng)度幾乎是呈線性增加的，然后再迅速衰減或者在一段時(shí)間內(nèi)強(qiáng)度保持恒定。HOLMES等[11]通過(guò)一個(gè)衰減函數(shù)乘以徑向速度，第一個(gè)提出了描述雷暴沖擊風(fēng)的時(shí)程曲線；CHAY等[12-13]更進(jìn)一步發(fā)展了之前的概念，并且引入了幾個(gè)強(qiáng)度衰減函數(shù)來(lái)描述風(fēng)速時(shí)程曲線。CHAY等[14]利用HJELMFELT等[15]的觀測(cè)結(jié)果給出了一個(gè)分析模型的強(qiáng)度衰減函數(shù)，他們認(rèn)為強(qiáng)度在前5～9 min內(nèi)線性增加，然后在接下來(lái)的5～9 min內(nèi)呈指數(shù)衰減(如圖1)。李錦華等[16]對(duì)雷暴沖擊風(fēng)非平穩(wěn)脈動(dòng)風(fēng)速進(jìn)行了數(shù)值合成，引入非均勻調(diào)制函數(shù)實(shí)現(xiàn)非平穩(wěn)脈動(dòng)風(fēng)速的時(shí)變功率譜。

本文基于沖擊射流三維足尺模型模擬雷暴沖擊風(fēng)場(chǎng)，在入口處引入一個(gè)更符合雷暴沖擊風(fēng)實(shí)際演化過(guò)程的衰減函數(shù)，采用大渦(LES)數(shù)值模擬獲得了雷暴沖擊風(fēng)的非穩(wěn)態(tài)風(fēng)場(chǎng)，并得到其隨時(shí)間衰減的瞬態(tài)演化過(guò)程。

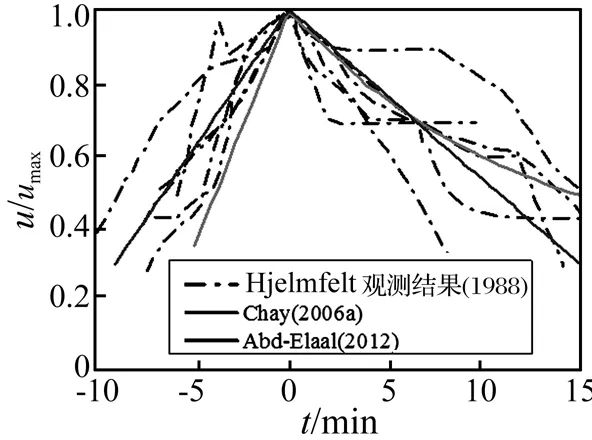
圖1 雷暴沖擊風(fēng)出流強(qiáng)度隨時(shí)間變化的實(shí)測(cè)記錄[15]Fig.1 Normalized radial velocity versus time[15]

1 CFD數(shù)值模擬

用計(jì)算流體力學(xué)軟件Fluent14.0來(lái)模擬不可壓縮的雷暴沖擊風(fēng)場(chǎng)，采用沖擊射流模型作為雷暴沖擊風(fēng)的基本風(fēng)場(chǎng)模型。為了盡可能反映真實(shí)物理尺度的雷暴沖擊風(fēng)現(xiàn)象，建立三維足尺計(jì)算域來(lái)模擬非穩(wěn)態(tài)沖擊射流場(chǎng)，模型參數(shù)包括：初始出流直徑Djet=600 m，計(jì)算入口到地面的距離Hjet=2Djet，邊界到噴口中心的徑向距離R=6Djet，計(jì)算域示意圖如圖2(a)，(b)所示。

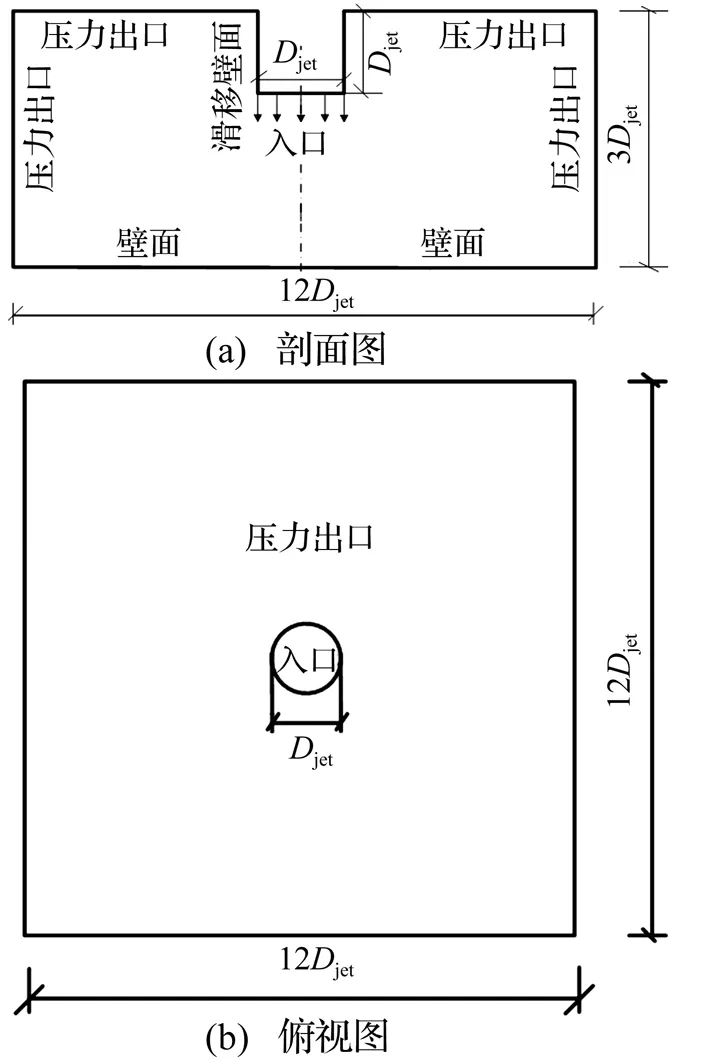
圖2 計(jì)算域示意圖Fig.2 The view of the computational domain

為了得到精確的數(shù)值模擬結(jié)果，采用結(jié)構(gòu)化網(wǎng)格劃分計(jì)算域，在沖擊射流中心區(qū)域采用4層O型網(wǎng)格，在近壁面區(qū)域滿足無(wú)量綱距離y+≈1，y+定義為[17]：

(1)

式中:Δy為首層網(wǎng)格到壁面的最小距離，單位m；ν指空氣的運(yùn)動(dòng)黏性系數(shù)，單位m2/s；τw為壁面切應(yīng)力，單位Pa；ρ為空氣的密度，單位kg/m3。

計(jì)算域網(wǎng)格數(shù)量約為1.2×107；速度入口取湍流強(qiáng)度I=1%；頂部及側(cè)邊均為壓力出口，壓力為1.013×105Pa；近地面壁面采用增強(qiáng)壁面處理模型；滑移壁面剪應(yīng)力取為0。

選用大渦模型(LES)對(duì)沖擊射流計(jì)算域進(jìn)行求解。該方法將湍流的大渦和小渦分開(kāi)處理，大漩渦直接求解Navier-Stokes方程，而小渦采用湍流模型來(lái)解決。沖擊射流模擬計(jì)算的時(shí)間步長(zhǎng)為0.1 s，總迭代步數(shù)6 000步，總計(jì)算時(shí)長(zhǎng)T=10 min。空氣密度為1.25 kg/m3，黏性系數(shù)為1.789 4×10-5Ns/m2。

2 速度入口函數(shù)

實(shí)際的雷暴沖擊風(fēng)其速度入口出流風(fēng)速隨時(shí)間是連續(xù)變化的，一般有一個(gè)先逐漸增大到最大值然后再逐漸減小的過(guò)程。Abd-Elaal[14]定義了一個(gè)速度入口分段函數(shù)為：第一段為恒定值，第二段直接減小到接近于0，來(lái)描述沖擊風(fēng)的衰減過(guò)程。本文為更加真實(shí)地重現(xiàn)雷暴沖擊風(fēng)的衰減過(guò)程，定義依然采用兩段的分段函數(shù)來(lái)表示速度入口，具體為：第一個(gè)時(shí)間段Δt1內(nèi)仍然為恒定值30 m/s；第二個(gè)時(shí)間段Δt2內(nèi)為呈指數(shù)逐漸減小到0，函數(shù)表達(dá)式為：

(2)

為了系統(tǒng)地考慮沖擊風(fēng)衰減周期對(duì)整個(gè)風(fēng)場(chǎng)的影響，這里第一個(gè)時(shí)間段Δt1選取2 min，3 min和4 min三種情況，對(duì)應(yīng)的第二個(gè)時(shí)間段Δt2=T-Δt1分別為8 min，7 min和6 min，速度入口速度變化函數(shù)曲線如圖3所示。

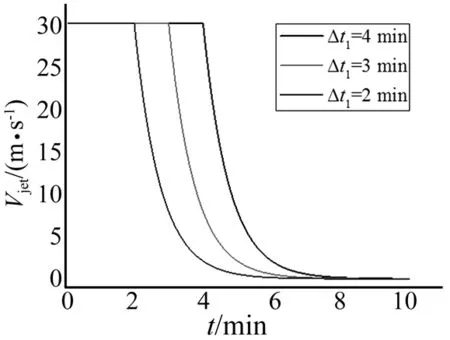
圖3 入口速度變化曲線Fig.3 Inlet velocityversus time

3 非穩(wěn)態(tài)計(jì)算結(jié)果及分析

3.1 穩(wěn)定階段平均風(fēng)速剖面

上述三種情況CFD數(shù)值模擬結(jié)果的穩(wěn)定階段(即Δt1段的后30 s風(fēng)速)水平向平均風(fēng)剖面與各個(gè)分析模型，經(jīng)驗(yàn)?zāi)Ｐ秃蛯?shí)測(cè)數(shù)據(jù)豎直風(fēng)剖面和徑向風(fēng)剖面進(jìn)行對(duì)比如下圖4、5所示。CFD模擬結(jié)果選取r=1.5Djet處的水平風(fēng)豎直剖面和z=0.01Djet高度處的水平風(fēng)徑向剖面，與Oseguera和Bowles模型[2]、Vicroy模型[3]、Wood和Kwok模型[4]、Hjelmfelt實(shí)測(cè)數(shù)據(jù)[10]和Letchford和Illidge[18]的物理實(shí)驗(yàn)?zāi)Ｐ偷冉Y(jié)果進(jìn)行對(duì)比，其中z為豎向高度，zm為最大水平風(fēng)速對(duì)應(yīng)的豎向高度，u為沿徑向的水平風(fēng)速，um為沿徑向水平風(fēng)速最大值，r為相對(duì)噴口中心的徑向距離，rm為最大水平風(fēng)速對(duì)應(yīng)的徑向距離。

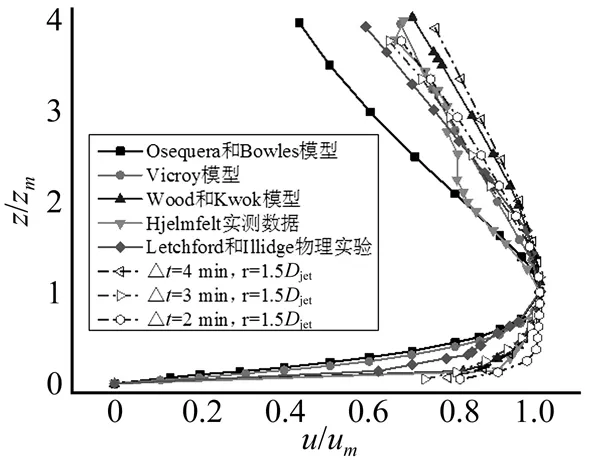
圖4 CFD數(shù)值模擬與各模型豎直風(fēng)剖面比較Fig.4 Comparison of vertical wind profile of CFD numerical simulation and analytical models

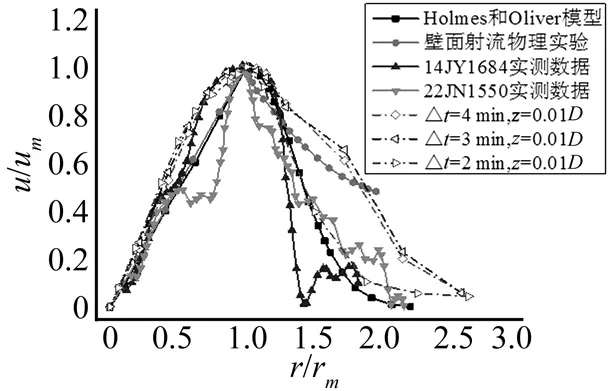
圖5 CFD數(shù)值模擬與各模型徑向風(fēng)剖面比較Fig.5 Comparison of radial wind profile of CFD numerical simulation and analytical models

從圖中可以看出各個(gè)分析模型，經(jīng)驗(yàn)?zāi)Ｐ秃蛯?shí)測(cè)數(shù)據(jù)與本文CFD模擬結(jié)果都給出了雷暴沖擊風(fēng)水平風(fēng)豎直剖面和徑向剖面的主要特征。在水平風(fēng)豎直剖面方面，由于本文是基于沖擊射流模型的模擬結(jié)果，所以和基于沖擊射流模型的物理實(shí)驗(yàn)得出的Wood和Kwok模型基本一致。在水平風(fēng)徑向剖面方面，CFD數(shù)值模擬結(jié)果對(duì)達(dá)到最大水平風(fēng)速后風(fēng)速衰減段的風(fēng)速值過(guò)高估計(jì)，主要原因是實(shí)際的沖擊風(fēng)經(jīng)歷形成、持續(xù)并最終擴(kuò)散的過(guò)程，并沒(méi)有停留在穩(wěn)定的狀態(tài)，CFD數(shù)值模擬是提取的風(fēng)場(chǎng)穩(wěn)定階段的數(shù)據(jù)。總體來(lái)說(shuō)，基于LES瞬態(tài)風(fēng)場(chǎng)數(shù)值模擬平均水平風(fēng)剖面同經(jīng)驗(yàn)風(fēng)剖面及實(shí)測(cè)數(shù)據(jù)吻合較好，在缺乏實(shí)測(cè)數(shù)據(jù)的情況下，除了風(fēng)洞試驗(yàn)可以提供較近似的結(jié)果外，基于LES的雷暴沖擊風(fēng)場(chǎng)數(shù)值模擬有利于了解其發(fā)展全過(guò)程尤其是達(dá)到最大水平風(fēng)速前流場(chǎng)的特性。

3.2 流場(chǎng)風(fēng)速云圖和矢量場(chǎng)

選取Δt1=3 min時(shí)的數(shù)值分析結(jié)果，沖擊射流下沉，發(fā)展，穩(wěn)定和衰減階段的速度云圖和矢量圖如圖6(a)～(f)所示。從圖中可以看到，在t=1 min時(shí)，速度入口下沉氣流與周?chē)鷼怏w之間拖拽卷吸，在下沉氣流周?chē)纬森h(huán)形漩渦(a)；在t=2 min時(shí)，入口速度保持30 m/s不變，環(huán)形漩渦沖擊地面后沿徑向水平發(fā)展，風(fēng)場(chǎng)迅速向周?chē)椛鋽U(kuò)散，在近地面達(dá)到最大出流強(qiáng)度(b)；在3 min過(guò)后，入口速度開(kāi)始減小，到3.5 min時(shí)，入口速度下降到最初的50%，整個(gè)風(fēng)場(chǎng)從入口位置開(kāi)始逐漸衰減，近地面出流強(qiáng)度逐漸減小(c),(d)；從4.5 min到5.5 min，入口速度迅速減小到接近為零，此時(shí)整個(gè)風(fēng)場(chǎng)都迅速衰減，隨著近地面出流強(qiáng)度的進(jìn)一步減弱，雷暴沖擊風(fēng)逐漸消退(e),(f)。

圖6 沖擊射流各時(shí)刻風(fēng)度云圖和矢量場(chǎng)Fig.6 The contour and vector plot of impinging jet at different time

3.3 水平風(fēng)速的瞬態(tài)分布

選取Δt1=3 min時(shí)的數(shù)值分析結(jié)果來(lái)考察雷暴沖擊風(fēng)整個(gè)過(guò)程水平風(fēng)速的瞬態(tài)分布情況。

3.3.1 豎直分布

雷暴沖擊風(fēng)水平風(fēng)速的豎直分布表征了水平風(fēng)速沿高度的變化規(guī)律，對(duì)結(jié)構(gòu)風(fēng)工程有重要參考價(jià)值。為了細(xì)致的考察沖擊風(fēng)整個(gè)過(guò)程，圖7給出了沖擊射流發(fā)展過(guò)程中不同徑向位置上水平風(fēng)速的豎直分布情況。從圖7中可以看到在雷暴沖擊風(fēng)沖擊地面前后和衰減過(guò)程中不同徑向位置水平風(fēng)速的豎直分布呈現(xiàn)較大差異。隨著下沉氣流沖擊地面并沿地面像四周擴(kuò)展，水平環(huán)形渦流一次經(jīng)過(guò)距離沖擊中心由近至遠(yuǎn)的各個(gè)徑向位置，導(dǎo)致超過(guò)一定高度后出現(xiàn)負(fù)向的速度。總體而言，各個(gè)徑向位置的最大水平風(fēng)速在2～3 min左右迅速增加到最大值，然后隨著時(shí)間增加逐漸減小，到5 min左右以后在整個(gè)豎向位置都下降到最大風(fēng)速的40%以?xún)?nèi)。

3.3.2 徑向分布

雷暴沖擊風(fēng)水平風(fēng)速的徑向分布表征了水平風(fēng)速沿徑向的變化規(guī)律，圖8給出了沖擊射流發(fā)展過(guò)程中不同高度位置上水平風(fēng)速?gòu)较蚍植记闆r。從圖8中可以看到，雷暴沖擊風(fēng)沖擊地面后在結(jié)構(gòu)風(fēng)工程關(guān)心的高度范圍內(nèi)水平風(fēng)速的徑向分布具有相似的規(guī)律，最大水平風(fēng)速出現(xiàn)在2 min左右，位于r=1.5Djet位置附近。然后隨著時(shí)間的增加，水平風(fēng)速逐漸減小，到5 min左右以后在整個(gè)徑向位置都下降到最大風(fēng)速的40%以下，這點(diǎn)跟豎直分布所觀察到的一樣，說(shuō)明雷暴沖擊風(fēng)在最大風(fēng)速衰減2 min左右整個(gè)風(fēng)場(chǎng)水平風(fēng)速都迅速減小到最大值的40%以下。

3.4 豎向風(fēng)速的瞬態(tài)分布

選取Δt1=3 min時(shí)的數(shù)值分析結(jié)果來(lái)考察雷暴沖擊風(fēng)整個(gè)過(guò)程豎向風(fēng)速的瞬態(tài)分布情況。

3.4.1 豎直分布

雷暴沖擊風(fēng)豎向風(fēng)速的豎直分布表征了豎向風(fēng)速沿高度的變化規(guī)律，為了細(xì)致的考察沖擊風(fēng)整個(gè)過(guò)程，圖9給出了沖擊射流發(fā)展過(guò)程中不同徑向位置上豎向風(fēng)速的豎直分布情況。從圖9中可以看到在雷暴沖擊風(fēng)沖擊地面前后和衰減過(guò)程中不同徑向位置豎向風(fēng)速的豎直分布呈現(xiàn)較大差異。隨著下沉氣流沖擊地面并沿地面像四周擴(kuò)展，水平環(huán)形渦流一次經(jīng)過(guò)距離沖擊中心由近至遠(yuǎn)的各個(gè)徑向位置，在水平環(huán)形渦流經(jīng)過(guò)的徑向位置，無(wú)論是風(fēng)速值還是風(fēng)向，豎向風(fēng)速的豎直分布呈現(xiàn)出較大的變化。總體而言，靠近噴口中心的r=0.6Djet在1 min內(nèi)就很快達(dá)到了最大值；r=1.0Djet和r=1.5Djet位置都是在2 min內(nèi)達(dá)到最大值，然后隨著時(shí)間增加而逐漸減小；而離噴口中心較遠(yuǎn)的r=2.0Djet位置各個(gè)時(shí)刻的豎向風(fēng)速都比較小，基本都在0.2Vjet范圍以?xún)?nèi)，由此可知，豎向風(fēng)速的影響范圍主要到達(dá)1.5Djet左右。

圖7 沖擊射流全過(guò)程各徑向位置水平風(fēng)速的豎直分布Fig.7 Vertical profiles of radial velocity at different time and different radial distances

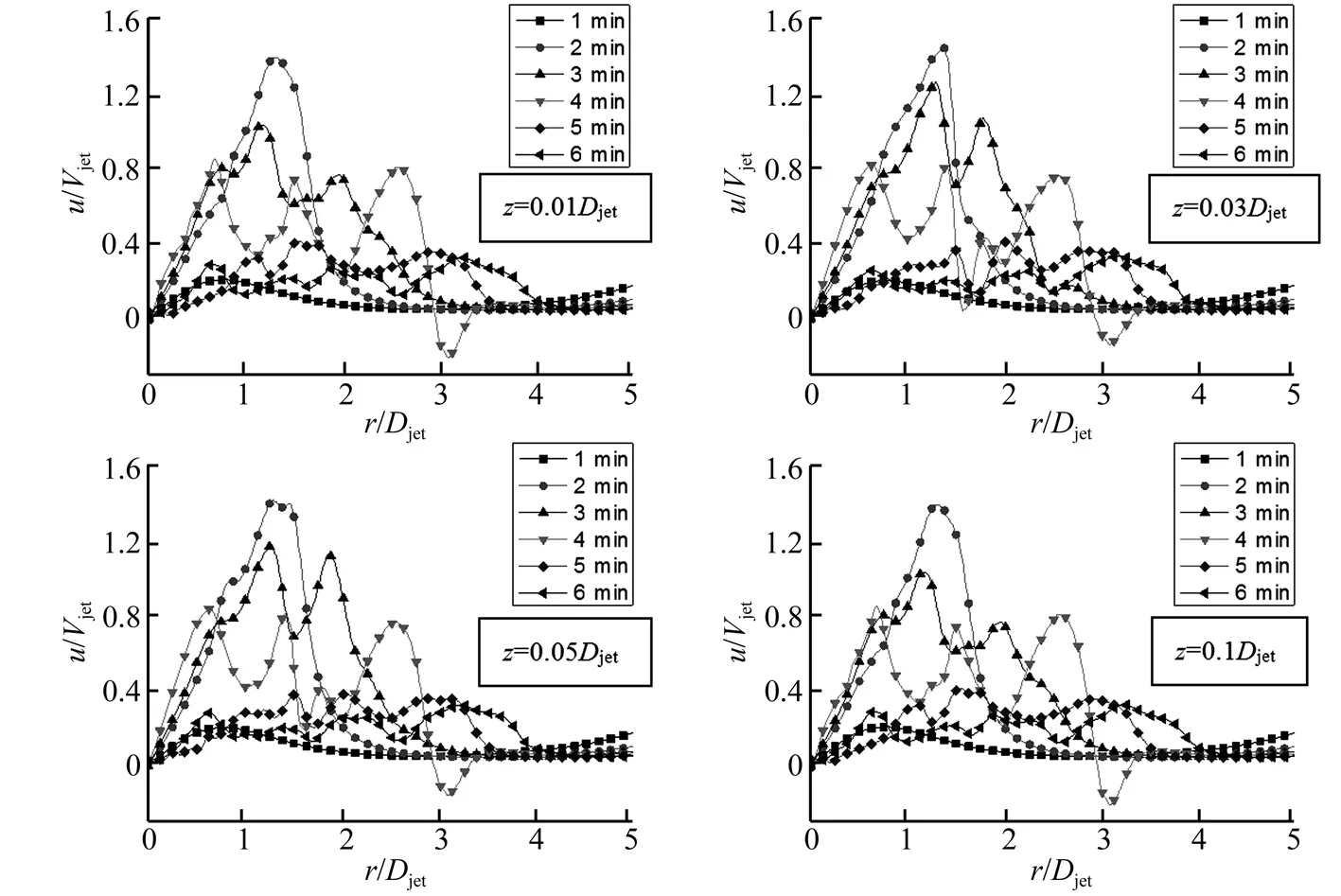
圖8 沖擊射流過(guò)程中各高度位置水平風(fēng)速的徑向分布Fig.8 Radial profiles of radial velocity at different time and different heights

3.4.2 徑向分布

雷暴沖擊風(fēng)豎向風(fēng)速的徑向分布表征了豎向風(fēng)速沿徑向的變化規(guī)律，圖10給出了沖擊射流發(fā)展過(guò)程中不同高度位置上豎向風(fēng)速?gòu)较蚍植记闆r。從圖10中可以看到，雷暴沖擊風(fēng)沖擊地面后在結(jié)構(gòu)風(fēng)工程關(guān)心的高度范圍內(nèi)豎向風(fēng)速的徑向分布形狀上具有相似的規(guī)律，最大豎向風(fēng)速出現(xiàn)在2 min左右，位于r=1.5Djet位置附近，但最大值的峰值大小有較大差異。然后隨著時(shí)間的增加，豎向風(fēng)速逐漸減小，到5 min左右在整個(gè)徑向位置的風(fēng)速值都下降到0.1Vjet以下。

3.5 水平速度和豎向速度時(shí)變特性

數(shù)值模擬結(jié)果水平速度在Δt1=2,3,4 min三種情況下的時(shí)程曲線如圖11所示(徑向位置r=1.0Djet，高度位置z=0.03Djet處)。可以看到三種情況下都有環(huán)形渦流經(jīng)過(guò)，導(dǎo)致在2 min左右達(dá)到了出流的最大強(qiáng)度，隨著Δt1的增加出流強(qiáng)度沒(méi)有更進(jìn)一步的增加。當(dāng)入口速度開(kāi)始下降的時(shí)候，監(jiān)測(cè)點(diǎn)速度并沒(méi)有突然的下降，而是保持了一段時(shí)間的穩(wěn)定值然后再開(kāi)始下降進(jìn)入衰減階段。

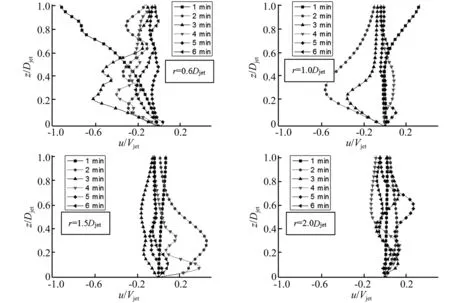
圖9 沖擊射流全過(guò)程各徑向位置豎向風(fēng)速的豎直分布Fig.9 Vertical profiles of vertical velocity at different time and different radial distances

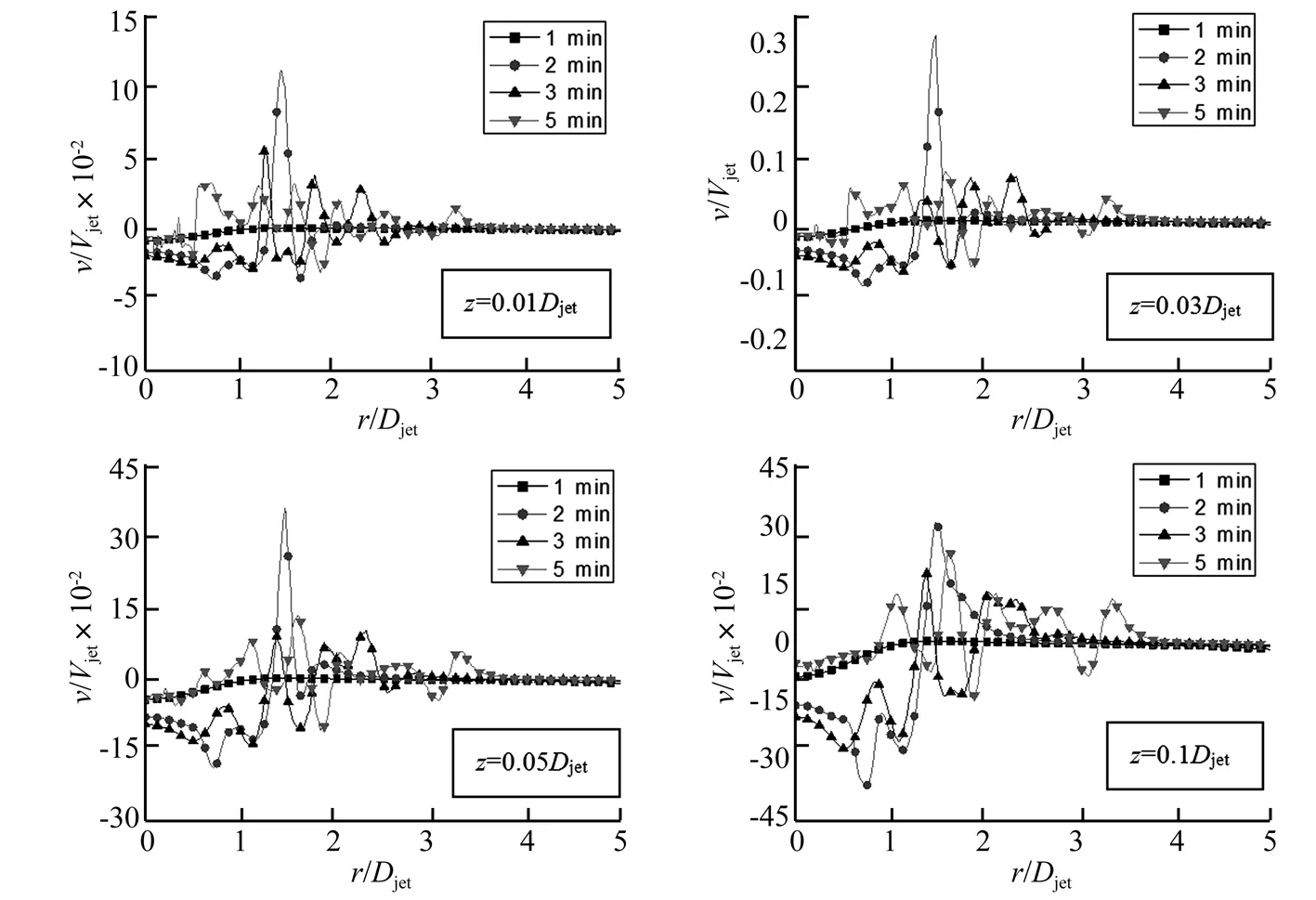
圖10 沖擊射流過(guò)程中各高度位置豎向風(fēng)速的徑向分布Fig.10 Radial profiles of vertical velocity at different time and different heights

選取Δt1=3 min時(shí)的數(shù)值分析結(jié)果來(lái)考察雷暴沖擊風(fēng)整個(gè)過(guò)程風(fēng)速的時(shí)變特性。在徑向r=1.0Djet處結(jié)構(gòu)工程比較關(guān)心的高度范圍內(nèi)(如z=0.002、0.005、0.025、0.1Djet)的水平風(fēng)速和豎向風(fēng)速時(shí)程曲線如圖12、13所示；在高度z=0.01Djet處各個(gè)徑向位置(如r=1.0、1.5、2.0、2.5、3.0Djet)的水平風(fēng)速和豎向風(fēng)速時(shí)程曲線如圖14和15所示。

圖12展示了速度強(qiáng)度時(shí)程曲線隨高度的改變，速度強(qiáng)度剛開(kāi)始隨著高度的增加而增大，直到最大速度所在高度位置然后減小，其變化趨勢(shì)和穩(wěn)態(tài)模型水平風(fēng)速的豎直風(fēng)剖面的變化趨勢(shì)一致；圖13展示了豎向風(fēng)速時(shí)程曲線隨高度的改變，速度強(qiáng)度隨高度連續(xù)的增加，其變化趨勢(shì)和穩(wěn)態(tài)模型豎向風(fēng)速的豎直風(fēng)剖面的變化趨勢(shì)也一致；圖14、15展示了速度強(qiáng)度時(shí)程曲線隨徑向距離的改變，速度強(qiáng)度隨徑向距離的增加而增大，到r=1.5Djet處達(dá)到最大值然后減小，其變化趨勢(shì)與穩(wěn)態(tài)模型水平風(fēng)速的徑向風(fēng)剖面也基本一致。

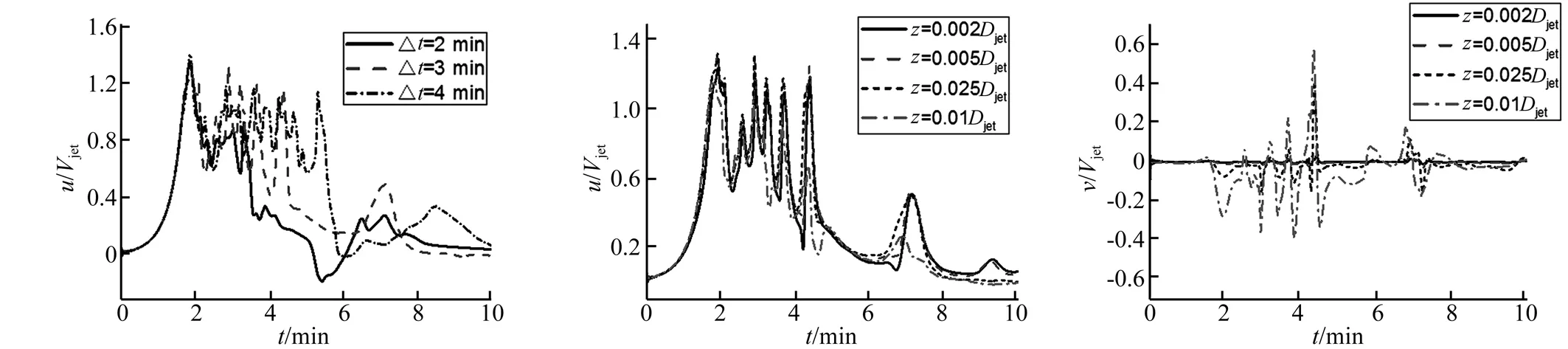
圖11 數(shù)值模擬時(shí)程曲線Fig．11Temporalprofilesoftheradialspeedforthreedifferentages圖12 r=1．0Djet各高度位置水平風(fēng)速時(shí)程曲線Fig．12Temporalradialspeedatr=1．0Djetfordifferentheights圖13 r=1．0Djet各高度位置豎向風(fēng)速時(shí)程曲線Fig．13Temporalverticalspeedatr=1．0Djetfordifferentheights

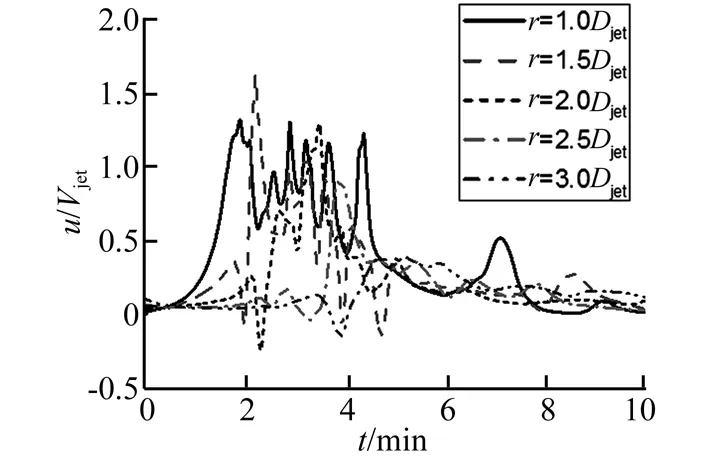
圖14 z=0.01Djet處各徑向位置水平風(fēng)速時(shí)程曲線Fig.14 Temporal radial speed at z=0.01Djetfor different radical locations

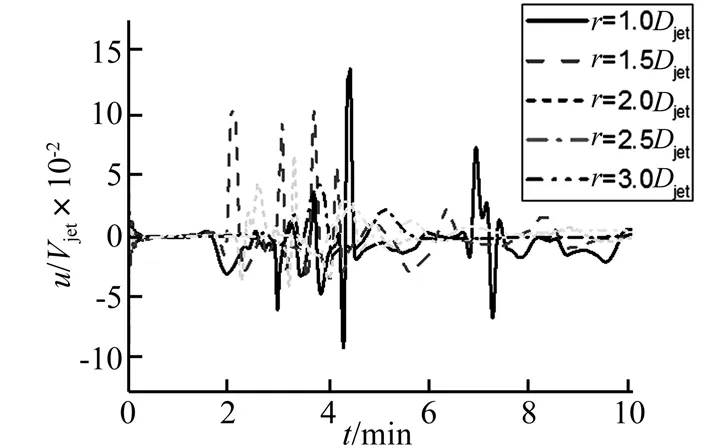
圖15 z=0.01Djet處各徑向位置豎向風(fēng)速時(shí)程曲線Fig.15 Temporal vertical speed at z=0.01Djet for different radical locations

4 結(jié) 論

利用大渦數(shù)值模擬方法，基于沖擊射流模型完成了三維足尺的雷暴沖擊風(fēng)非穩(wěn)態(tài)模擬。在CFD計(jì)算結(jié)果與相關(guān)經(jīng)驗(yàn)、分析模型和實(shí)測(cè)數(shù)據(jù)進(jìn)行比較以驗(yàn)證CFD數(shù)值模型及參數(shù)準(zhǔn)確性的基礎(chǔ)上，進(jìn)行了風(fēng)場(chǎng)特性的全面研究。在速度入口處引入一個(gè)更符合雷暴沖擊風(fēng)演化過(guò)程的速度衰減函數(shù)，得到了沖擊風(fēng)場(chǎng)整個(gè)生命周期及衰減過(guò)程的詳細(xì)信息。結(jié)構(gòu)風(fēng)工程關(guān)心的沖擊風(fēng)近地面風(fēng)場(chǎng)的水平風(fēng)速和豎向風(fēng)速總體而言都在短時(shí)間內(nèi)迅速達(dá)到最大值，隨后逐漸衰減或保持一個(gè)恒定值波動(dòng)后再迅速衰減至零。基于沖擊射流模型開(kāi)展的CFD瞬態(tài)數(shù)值模擬可以較好地體現(xiàn)雷暴沖擊風(fēng)整個(gè)衰減過(guò)程的基本特性，為進(jìn)一步討論非穩(wěn)態(tài)雷暴沖擊風(fēng)場(chǎng)中的結(jié)構(gòu)風(fēng)荷載奠定了基礎(chǔ)。

[ 1 ] 張勇. 輸電線路風(fēng)災(zāi)防御的現(xiàn)狀與對(duì)策[J]. 華東電力, 2006,34(3):28-31. ZHANG Yong. Status quo of wind hazard prevention for transmission lines and countermeasures [J]. East China Electric Power, 2006,34(3):28-31.

[ 2 ] 瞿偉廉，吉柏鋒. 下?lián)舯┝鞯男纬膳c擴(kuò)散及其對(duì)輸電線塔的災(zāi)害作用[M]. 北京：科學(xué)出版社，2013.

[ 3 ] OSEGUERA R M, BOWLES R L. A simple analytic 3-dimensional downburst model based on boundary layer stagnation inflow [R].NASA Technical Memorandum 100632, 1988.

[ 4 ] VICROY D D.A simple, analytical, asymmetric microburst model for downdraft estimation [R]. NASA Technical Memorandum 104053, 1991.

[ 5 ] WOOD G S, KWOK K C S, An empirically derived estimate for the mean velocity profile of a thunderstorm downbursts [C]//Proceedings of 7th AWES Workshop. Auckland, 1988.

[ 6 ] HOLMES J D, OLIVER S E. An empirical model of a downburst [J].Engineering Structures, 2000, 22: 1167-1172.

[ 7 ] SHEHATA A Y, EL DAMATTY A A, Savory E. Finite element modeling of transmission line under downburst wind loading [J]. Finite Elements in Analysis and Design, 2005, 42(1):71-89.

[ 8 ] ABD-ELAAL E, MILLS J E, MA X. A coupled parametric-CFD study for determining ages of downbursts through investigation of different field parameters [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 30-42.

[ 9 ] FUJITA T T. The downburst report of Projects NIMROD and JAWS [R]. Chicago: University of Chicago, 1985.

[10] HJELMFELT M R. Structure and life circle of microburst outinflows observed in Colorado[J]. J. ApplMeteorol, 1988, 27(8): 900-927.

[11] HOLMES J D, OLIVER S E. An Emprical Model of a Downburst[J].Engineering Structures, 2000, 22:1167-1172.

[12] CHAY M T, ALBERMANI F, WILSON R. Numerical and analytical simulation of downburst wind loads [J]. Engineering Structures, 2006, 28(2): 240-254.

[13] ABD-ELAAL E, MA X, MILLS J E. A newly developed analytical model of transient downburst wind loads [C]//Proceedingsof the 22th Australian Conference on the Mechanics of Structures and Material, Sydney, Australia, 2012: 425-430.

[14] ABD-ELAAL E, MILLS J E, MA X. Empirical models for predicting unsteady-state downburst wind speeds [J]. J. Wind Eng. Ind. Aerodyn, 2014, 129: 49-63.

[15] WILSON J W, ROBERTS R D, KESSINGER C, et al. Microburst wind structure and evaluation of Doppler radar for airport wind shear detection [J]. Journal of Climate and Applied Meteorology, 1984, 23(6):898-915.

[16] 李錦華，吳春鵬，陳水生.下?lián)舯┝鞣瞧椒€(wěn)脈動(dòng)風(fēng)速數(shù)值模擬[J]. 振動(dòng)與沖擊，2014, 33(14):54-60. LI Jinhua，WU Chunpeng，CHEN Shuisheng. Simulation of non-stationary fluctuating wind velocity in downburst[J]. Journal of Vibration and Shock,2014, 33(14):54-60.

[17] Fluent Inc. FLUENT User’s Guide[Z]. Fluent Inc., 2003.

[18] LETCHFORD C W, ILLIDGE G. Turbulence and topographic effects in simulated thunderstorm downdrafts by wind tunnel jet[C]//Proceedings of the Tenth International Conference on Wind Engineering, Denmark, June 1999:1907-1912.

Transient numerical simulation for unsteady-state downburst winds

WANG Zhisong1,2,WANG Chao3, LIU Yanan1, LI Zhengliang1,2

(1. School of Civil Engineering, Chongqing University, Chongqing 400045, China;2. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing University, Chongqing 400045, China;3. Hunan Provincial Architectural Design Institute, Changsha 410001, China)

Impinging jet is one of the most commonly used simulation methods in studying the wind field of thunderstorms. Most of the previous physical tests and numerical simulations assume that the inlet velocity of the jet does not change with time, while the sinking velocity of downburst winds is continuously changing with time actually during its whole lifecycle, it gradually increases to the maximum value and then decreases in general. For wind-resistant design of significant engineering structures, it’s necessary to acquire the temporal profiles of downburst wind speed in its whole lifecycle. Here, a three-dimensional full-scale impinging jet was taken as a wind field model of downburst. The decay functions for the inlet jet velocity were given for the actual downburst，and numerical simulation was performed by adopting the large eddy simulation(LES) to acquire an unsteady-state wind field where the intensity decay information of downburst was presented. The simulation results showed that the unsteady wind field of downburst can be well simulated with this proposed method, and the results are correlated well to Andrews AFB recorded ones. These results laid a foundation for further studying wind load characteristics of unsteady downburst.

downburst; unsteady-state; impinging jet; LES; numerical simulation

國(guó)家自然科學(xué)基金(51208537)

2015-10-09 修改稿收到日期：2016-01-27

汪之松 男，副教授，1980年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.03.009