基于判別信息極限學習機的高光譜遙感圖像分類

楊伊+閆德勤+張海英+楚永賀

摘要摘要：極限學習機（ELM）以其高效、快速和良好的泛化性能在模式識別領域得到廣泛應用，然而在高光譜遙感圖像分類中，極限學習機算法不能較好地利用數據蘊含的判別信息，限制了ELM的分類性能。為此，提出一種基于判別信息極限學習機（IELM），IELM繼承了極限學習機的優勢，并在一定程度上解決了極限學習機在有限高光譜遙感圖像數據樣本中學習不充分的問題。高光譜遙感圖像分類實驗結果表明，該算法具有較好的分類效果。

關鍵詞關鍵詞：極限學習機；模式識別；高光譜遙感圖像；判別信息

DOIDOI：10.11907/rjdk.162600

中圖分類號：TP317.4文獻標識碼：A文章編號文章編號：16727800（2017）001016105

對于連續狹窄的光譜帶，高光譜成像傳感器能夠捕獲詳細和豐富的光譜信息。近年來，隨著圖像處理技術的發展，高光譜圖像得到廣泛應用，在高光譜圖像應用中最重要的任務是對圖像進行分類。然而，在高光譜遙感圖像分類問題中存在一些挑戰。例如有限訓練樣本之間的不平衡和高維度，高光譜遙感圖像幾何形狀復雜，高光譜遙感圖像分類計算復雜度高。為使高光譜遙感圖像分類取得良好效果，近年來，機器學習方法在高光譜圖像分類中得到廣泛應用，例如人工神經網絡（Artificial neural networks，ANNs）[1]、支持向量機（Support vector machine，SVM）[2]、多項邏輯回歸（Multinomial logistic regression，MLR）[3]、主動學習（Active learning，AL）[4]等，其它方法如利用稀疏表示[5]以及譜聚類[6]對高光譜進行分離也得到廣泛應用。然而，由于高光譜遙感圖像具有髙維度以及復雜性，通過機器學習算法尋找最優的參數來進行分類通常非常困難，并且耗時，實現高光譜遙感圖像高效快速分類已成為遙感圖像領域的重要問題。

近年來，Huang等[7]基于單隱層前饋神經網絡（Single-hidden layer feedforward networks，SLFNs）結構提出了極限學習機（Extreme learning machine，ELM）。ELM隨機產生隱層節點的輸入權值和偏置值，所有參數中僅有輸出權值經過分析確定。ELM將傳統神經網絡的求解過程轉化為一個線性模型，ELM隨機選擇輸入權值和分析確定SLFNs的輸出權值，避免了傳統神經網絡學習方法收斂速度慢及陷入局部極小解的可能，具有更好的泛化能力和更快的學習速度。文獻[7]指出ELM通過隨機產生隱層節點的輸入權值和偏置值分析確定輸出權值，保持了SLFNs的通用逼近能力，同時能夠得到一個全局最優解。由于ELM良好的泛化能力，使得ELM應用在不同的領域中。在高光譜遙感圖像領域，Pal等[8]將ELM應用到土地覆蓋分類中，與BP[9]神經網絡和支持向量機相比，ELM取得了更好的分類效果，并且ELM算法的計算復雜度遠遠小于BP和支持向量機。Bazi等[10]利用差分進化方法優化核ELM算法的參數，提高了高光譜遙感圖像的分類效果。為了提高ELM算法在高光譜遙感圖像分類中的穩定性，Samat等[11]基于Bagging 和 AdaBoost算法提出了集成的極限學習機算法（Ensemble extreme learning machine，E2LM）。

雖然針對高光譜遙感圖像分類問題，研究人員在ELM算法的基礎上提出了改進，然而 ELM及其改進算法并未充分考慮數據樣本間的幾何特征和數據蘊含的判別信息。知道樣本之間具有某些相似的屬性和分布特征，樣本之間的相似屬性和分布特征能夠彌補ELM學習不夠充分的問題，進而可以提高ELM的泛化能力，因而數據樣本的幾何特征和數據蘊含的判別信息對ELM的分類性能具有重要作用。

基于以上分析，本文提出一種基于判別信息極端學習機（Discriminative information regularized extreme learning machine，IELM），對于分類問題，IELM同時考慮到數據樣本的幾何特征和數據蘊含的判別信息，通過最大化異類離散度和最小化同類離散度，優化極端學習機的輸出權值，從而在一定程度上提高ELM的分類性能和泛化能力。IELM方法的優勢在于：①繼承了ELM的優點，在一定程度上避免了ELM學習不充分的問題；②將異類離散度和同類離散度引入到ELM中，充分利用數據樣本的判別信息；③利用MMC[12]方法有效解決最大化異類離散度和最小化同類離散度矩陣奇異問題。

為評價和驗證本文提出的基于判別信息極端學習機的高光譜遙感圖像分類方法，實驗使用Indian Pines，Salinas scene兩個高光譜遙感圖像數據，將本文所提出的方法與ELM、支持向量機（Support vector machine，SVM）、最近鄰分類器協作表示（Collaborative representation nearest neighbor classifier，CRNN）[13]進行對比，實驗結果表明本文提出的算法能夠取得較好的分類效果。

實驗環境為惠普工作站處理器：Intel（R）Xeon（R） CPU E5-1603 0 @2.80 GHz，安裝內存：8.00GB ，系統類型：64位操作系統，版本：win7，語言開發環境采用 Matlab 2010b。

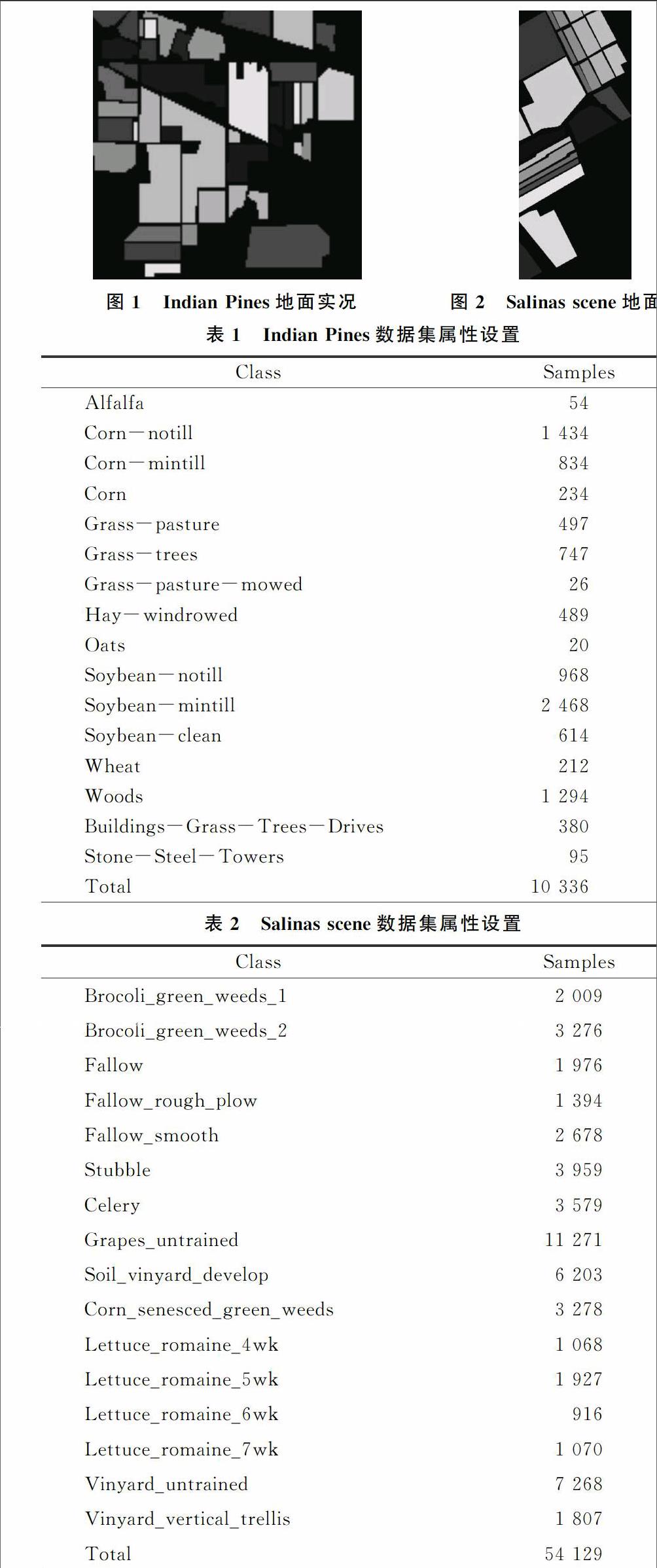
第一組實驗數據為Indian Pines遙感圖像數據，Indian Pines數據是AVIRIS傳感器在薩利納斯山谷收集的數據，該圖像包含200個波段，圖像大小為145×145，地表真實分類如圖1所示，Indian Pines數據集屬性設置如表1所示。

第二組實驗數據為Salinas scene遙感圖像數據，Salinas scene數據是AVIRIS傳感器在薩利納斯山谷收集的數據，該圖像包含204個波段，圖像大小為512×217，地表真實分類如圖2所示， Salinas scene數據集屬性設置如表2所示。

實驗中，對于Indian Pines和Salinas scene圖像數據，隨機選取1%的數據樣本作為訓練集，剩下部分為測試集，使用總體精度（OA），Kappa系數，平均準確率（AA）衡量不同算法的性能。

（1）總體精度。總體精度（overall accuracy，OA）是對分類結果質量的總體評價，等于被正確分類的像素總和除 以總的像素個數。被正確分類的像素沿著混淆矩陣的對角線分布，它顯示了被正確分類到真實分類中的像元數。根據混淆矩陣可得OA的計算式為：p=∑ci=1miiN（21）其中，c表示類別數目，mii表示混淆矩陣對角線上的元素，N=∑ci=1∑cj=1mij表示測試樣本的總數。

（2）Kappa系數。Kappa系數采用一種多元離散分析技術，反映分類結果與參考數據之間的吻合程度，它考慮了混淆矩陣的所有因子，是一種更為客觀的評價指標，其定義為：k=N∑ci=1mii-∑ci=1（mi+m+i）N2-∑ci=1（mi+m+i）（22）其中，mi+，m+i分別表示混淆矩陣第i行的總和、第i列的總和，c表示類別數目，N為測試樣本總數，mii表示混淆矩陣對角線上的元素，Kappa系數越大分類精度越高。

（3）平均精度。平均精度（average accuracy，AA）定義為每類分類準確率相加除以類別總數。AA=∑ci=1accic（23）其中，c表示類別數目，acci表示每類的分類準確率。

4.2實驗結果及分析

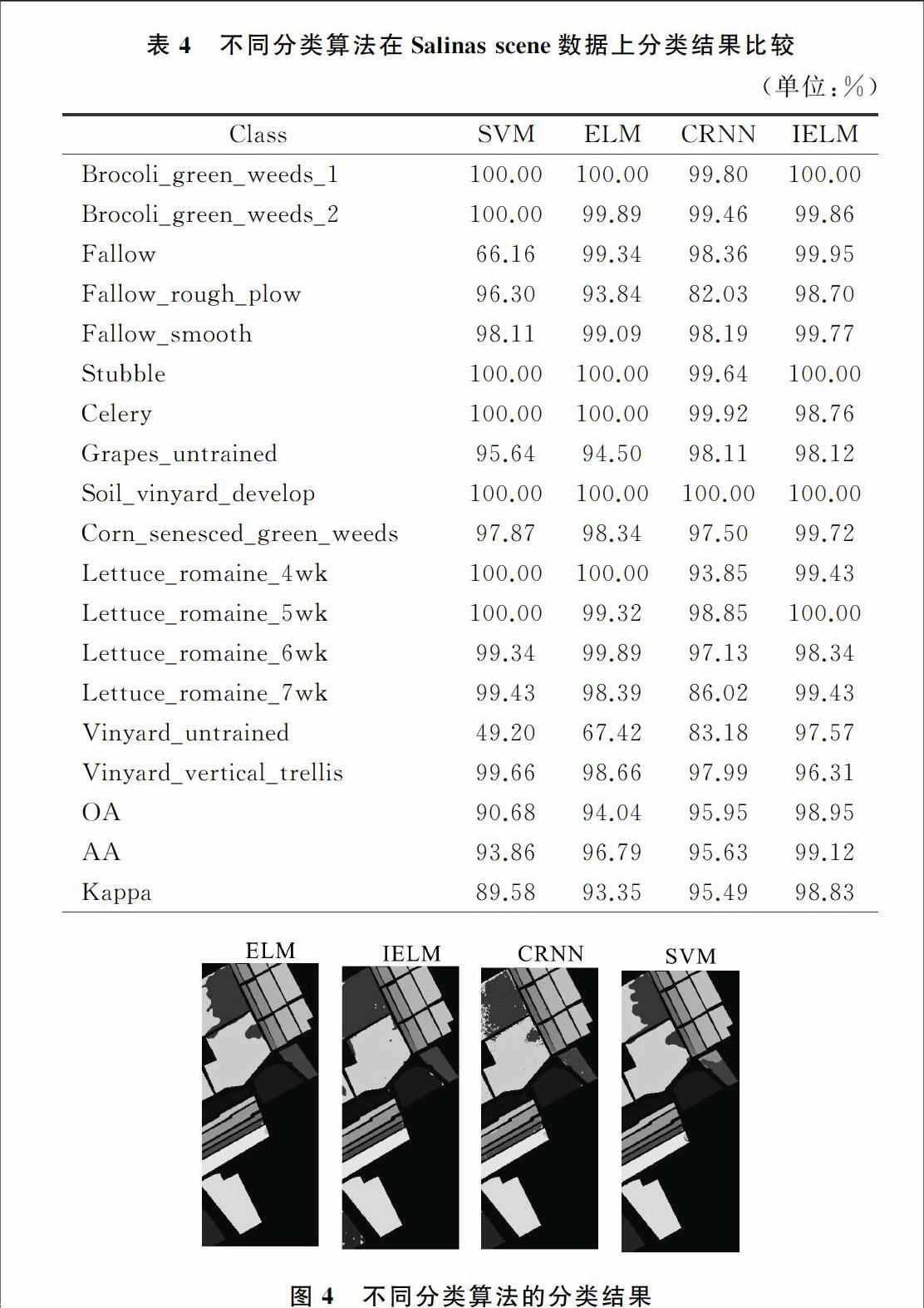
將IELM與ELM，SVM，CRNN進行對比，SVM采用libsvm工具箱，核函數采用徑向基核函數（Radial basis function，RBF），懲罰參數c=0.02，核函數參數g=0.02，IELM與ELM均采用Sigmoid函數作為激活函數，隱層節點個數設置為500，懲罰參數c=20。

5結語

本文提出了一種基于判別信息極端學習機的高光譜遙感圖像分類方法，創新之外在于考慮到光譜遙感圖像數據的聯系和差異信息。IELM引入同類離散度和異類離散度的概念，體現了輸入空間數據的判別信息，通過最大化異類離散度和最小化同類離散度，優化極端學習機的輸出權值。與NN，SVM， ELM算法的對比實驗表明，本文所提出方法的分類效果優于NN，SVM，ELM算法。

參考文獻：

[1]Q SAMI UL HAQ，L TAO.Neural network based adaboosting approach for hyperspectral data classication[J].International Conference on Computer Science and Network Technology（ICCSNT），2011：241245.

[2]J A GUALTI，R F CROMP.Support vector machines for hyperspectral remote sensing classification[J].in Proc.SPIE 27th AIPR Workshop：Adv.Comput.Assisted Recognit.Int.Soc.Opt.Photonics，Washington，DC，USA，1999：221232.

[3]J Li，J BIOUCASDIAS，A.PLAZA.Semisupervised hyperspectral image classification using soft sparse multinomial logistic regression[J].IEEE Geosci.Remote Sens.Lett，2013，10（2）：318322.

[4]W DI，MM CRAWFORD.Active learning via multiview and local proximity coregularization for hyperspectral image classification[J].IEEE Journal of Selected Topics in Signal Processing，2011，5（3）：618628.

[5]J BIOUCASDIAS，M A T.FIGUEIREDO.Alternating direction algorithms for constrained sparse regression：application to hyperspectral unmixing[J].Hyperspectral Image and Signal Processing：Evolution in Remote Sensing （WHISPERS），2010：14.

[6]Y TARABALKA，J A BENEDIKTSSON，J CHANUSSOT.Spectralspatial classification of hyperspectral imagery based on partitional clustering techniques[J].IEEE Transactions on Geoscience and Remote Sensing，2009，47（8）：29732987.

[7]GB HUANG，H ZHOU，X DING，et al.Extreme learning machine for regression and multiclass classification[J].IEEE Trans.Syst Man Cybern B，2012，42（2）：51329.

[8]M PAL，A E MAXWELL，T A WARNER.Kernelbased extreme learning machine for remotesensing image classification[J].Remote Sens.Lett，2013，4（9）：853862.

[9]D RUMELHART，G HINTON，R WILLIAMS.Learning by backpropagating errors[J].Nature，1986，323（6088）：533536.

[10]Y BAZI.Differential evolution extreme learning machine for the classification of hyperspectral images[J].IEEE Geosci.Remote Sens.Lett，2014，11（6）：10661070.

[11]A SAMAT，P DU，S LIU，et al.E2LMs：ensemble extreme learning machines for hyperspectral image classification[J].IEEE J.Sel.Topics Appl.Earth Observ.Remote Sens，2014，7（4）：10601069.

[12]H LI，T JIANG，K ZHANG.Efficient robust feature extraction by maximum margin criterion[J].IEEE Transactions on Neural Networks ，2006，17（1）：157165.

[13]W LI，Q DU，F ZHANG.Collaborativerepresentationbased nearest neighbor classifier for hyperspectral imagery[J].IEEE Geoscience and Remote Sensing Letters ，2015，12（2）：389393.

[14]G B HUANG.An insight into extreme learning machines：random neurons，random features and kernels[J].Cognitive Computation，2014，6（3）：376390.

責任編輯（責任編輯：陳福時）