Duffing混沌弱信號檢測系統分析及電路實現

曹滿婷, 宋菲菲

(燕山大學電氣工程學院工業計算機控制工程河北省重點實驗室，河北 秦皇島 066004)

Duffing混沌弱信號檢測系統分析及電路實現

曹滿婷, 宋菲菲

(燕山大學電氣工程學院工業計算機控制工程河北省重點實驗室，河北 秦皇島 066004)

采用Melnikov方法，對廣泛使用的Duffing混沌弱信號檢測系統進行了分析。通過Matlab軟件實現了數值仿真分析，利用Multisim實現了電路仿真分析。設計制作了Duffing混沌實際電路板，通過調試得到了較為理想的檢測性能。電路試驗結果驗證了Duffing混沌弱信號檢測系統可以通過電子線路實現。該系統對Duffing混沌弱信號檢測系統的實際工程應用具有促進作用，對其他混沌弱信號檢測領域的進一步研究具有較高的參考價值。

Duffing系統; 混沌算法; Matlab; 抗噪性; 高斯分布; 瑞利分布; 色噪聲

0 引言

當信號較微弱并且被淹沒在強噪聲環境中時，要提取真實的信號是相當困難的。傳統微弱信號檢測使用時域的方法，設備比較復雜。雖然檢測方法和儀器實現技術日趨成熟，但是信噪比門限值較高、設備昂貴，這大大限制了傳統微弱信號檢測的應用范圍。與傳統弱信號檢測系統相比，混沌弱信號檢測系統的信噪比和檢測門限可以達到更低的數量級。目前廣泛使用的Duffing混沌弱信號檢測系統由于很難通過電路實現，妨礙了它在弱信號檢測領域的應用。為了克服上述Duffing混沌弱信號檢測系統的不足，本文分析了Duffing混沌弱信號檢測系統的性能，并設計、制作了相應的電路[1-6]。

1 Duffing混沌弱信號檢測系統

1.1 系統性能理論分析

Duffing混沌系統是目前典型的、使用廣泛的混沌弱信號檢測系統。Duffing系統的基本動力學方程如下：

(1)

令a=1、b=1，則Holmes型Duffing公式為：

(2)

式中：k為阻尼比，令k=0.5；x-x3為非線性恢復力。

式(2)是一個哈密頓(Hamilton)系統，其哈密頓量表達式為：

(3)

當策動力幅值r=0時：

(4)

解得三個奇點為(0，0)、(1，0)、(1，0)。設系統的特征根為λ，系統特征方程為：

(5)

即：

λ2=1-3x2

(6)

此時，方程組可化為如下形式：

(7)

因為表達式x-x3中包含因子y，所以(0，0)為孤立奇點，也可以寫成：

(8)

因為an=1、h(x)=-x2、n=1，則(0，0)的性質由n決定。因為n=1=2×0+1，則根據Briot-Bouquet引理可知：當a2×0+1>1時，奇點(0，0)為鞍點。由上述分析可知，當系統的哈密頓量h=0時，存在兩條連結雙曲鞍點的同宿軌道。

(9)

當策動力幅值r不為0時，系統表現出復雜的動力學形態。當r較小時，相點在兩焦點附近作周期振動。隨著r的增大，系統遍歷同宿軌道、倍周期分岔軌道、混沌軌道；當r超過一定閾值時，系統為大周期軌道。

1.2 系統性能分析

通過相圖觀察及大量仿真，得出系統的策動力臨界值為0.826 59。隨著r的不斷增大，系統相平面輸出x、y經歷同宿軌道、倍周期分岔、混沌狀態以及大周期狀態。從Duffing系統隨時間變化的x、y時序圖、龐加萊映射圖以及隨頻率變化的功率譜圖和隨r變化的分岔圖可得:系統的時序圖無序，龐加萊映射圖中有成片的、分形的密集離散點，功率譜連續。由此可知，Duffing系統是一個典型的二階混沌系統。由分岔圖可知，Duffing系統在隨策動力幅值r逐漸增大的過程中，相點經歷“周期振動-混沌-大周期”的狀態。

Duffing系統弱信號檢測原理是利用相軌跡分析法，觀察相軌跡是否從混沌狀態變為大周期狀態，從而判斷是否有微弱正弦信號。具體檢測過程為：檢測信號前，先調節幅值r，使變量x或y的輸出電壓為混沌波形且接近混沌到大周期的臨界狀態。如果外部輸入同頻率的弱正弦(或余弦)波電信號，之后外部輸入微弱正弦波信號的幅值和r相加，使x或y輸出的電壓波形越過臨界點。當相點從混沌波形變為大周期波形，表示檢測到一個同頻率的微弱正弦波信號[7-8]。

1.3 不同包絡信號敏感度分析

由于實際測量中接收到的信號幅值會有一定變化，以下從指數分布、高斯分布、瑞利分布三種分布情況進行研究。幅值為指數分布的概率密度函數為：

(10)

式中：λ>0，且為常數，取λ為0.003。將系統設置為臨界振蕩狀態，加入指數分布的同頻信號，則可以看到系統由混沌狀態變為大周期狀態。

Duffing系統加入指數分布包絡信號后的輸出狀態如圖1所示。

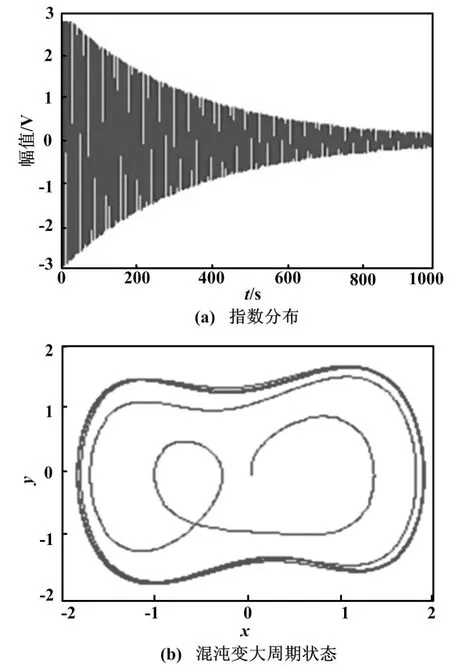
圖1 輸出狀態圖

高斯分布的概率密度函數為：

(11)

式中：σ>0,σ=200;a為常數,取a=500。

高斯分布曲線如圖2所示。

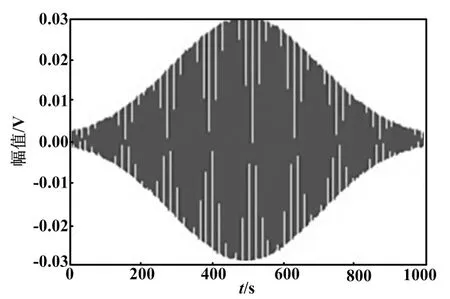
圖2 高斯分布曲線

瑞利分布的概率密度函數為：

(12)

式中：x≥0；σ為常數，取σ=300。

瑞利分布曲線如圖3所示。

圖3 瑞利分布曲線

以上分析表明：Duffing系統對弱信號極其敏感，適用于微弱信號檢測。

1.4 信噪比分析

微弱信號檢測的主要目的是提高信噪比。對于傳統的微弱信號檢測方法，如果信號頻帶和噪聲頻帶重疊，則在抑制噪聲的同時將不可避免地損害有用信號，甚至采用窄帶化技術也未必奏效。接下來分析Duffing系統的信噪比。

1.4.1 加入白噪聲

先將系統設置為臨界振蕩狀態，加入均值為0、方差為0.001的高斯白噪聲，結果表明，噪聲并不影響其混沌特性，只是變粗糙了。

將Duffing系統調節為臨界狀態，此時加入幅值為0.000 1的待測信號，同時加入均值為0、方差為10-6的高斯白噪聲，結果表明，噪聲并不影響其變為大周期。

1.4.2 加入色噪聲

采用方差為1、均值為0的高斯白噪聲，通過一個四階帶通濾波器產生高斯色噪聲。

該濾波器的傳遞函數為：

H(z)=[0.020 1(1-2z-2+z-4)]/(1-1.637z-1+2.237z-2-1.307z-3+0.641z-4)

(13)

該濾波器的上限截止頻率為0.2Hz，下限截止頻率為0.15Hz(均為歸一化角頻率)。

高斯色噪聲的功率為：

(14)

首先令噪聲放大器的增益u=1，待測正弦信號放大器的增益u=0，此時只加入內部正弦信號。調節系統內置信號的幅值f=fd，此時，該系統處于混沌臨界狀態。

加入色噪聲后，由系統的相平面軌跡圖可知，系統的相軌跡仍處在混沌狀態。雖然噪聲比較強，但是混沌吸引子仍然能夠將相點束縛在軌道內，說明混沌系統對噪聲具有免疫力。當所增加的噪聲強度達到一定值時，系統的相軌跡出現了毛刺，但是仍然處于混沌狀態，如圖4所示。使待測正弦信號增益放大器為1，調節待測正弦信號的幅值為1nV，調節高斯噪聲發生器的方差，使其方差為1×10-8，此時可以觀測到相平面的軌跡為大尺度周期狀態，如圖5所示[9]。

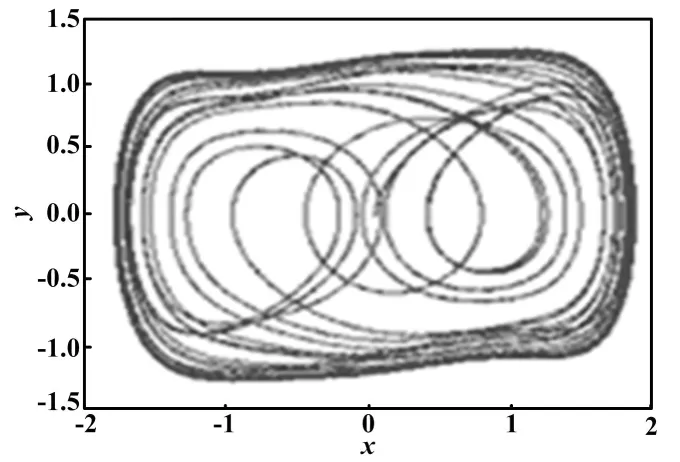
圖4 增大色噪聲的相圖

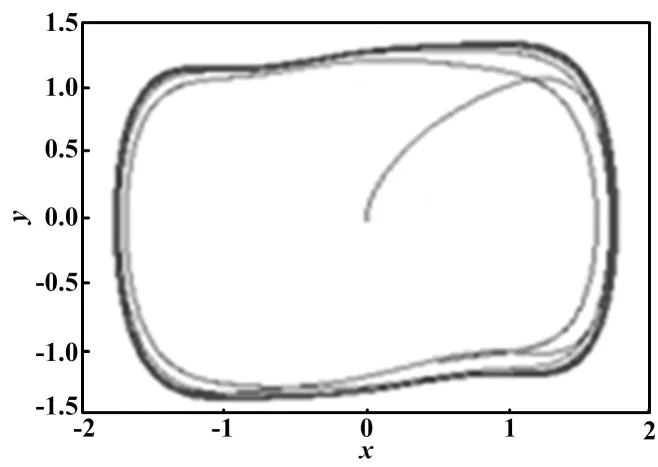
圖5 方差為1×10-8的相圖

當輸入色噪聲的功率為1×10-9W時，Duffing混沌檢測系統的最低檢測下限為20lg(1×10-9)=-180dB，檢測信噪比下限為：

(15)

混沌系統對噪聲有免疫力，而對周期信號卻很敏感，表現為周期信號可以使處于混沌狀態的相軌跡發生變化。

2 電路實現

利用Multisim進行電路仿真，設計中所有元件均采用真實元器件型號，應盡可能使仿真結果與實際電路保持高度一致性。運算放大器選擇偏置電流為2～100pA、輸入失調電壓為2～9mV的ADTL084，乘法器選擇精確度較高的AD734，電容選擇漏電小的薄膜電容[10-11]。

使用Duffing仿真電路進行試驗，調節系統閾值為0.825 56。然后，加入微弱待測信號：策動力為6 366.2Hz、幅值為0.84V的正弦波，在t為6～14ms、22～36ms及40～45ms的時刻加入6 366.2Hz的0.01V正弦波。當加入待測信號后，系統變為大周期狀態。經過多次調試與檢測發現，加入不同頻率的待測信號后，系統有時對其并不是很敏感，需要延遲一段時間后才會變為大周期。但是可以基本驗證Duffing混沌系統在有弱正弦信號輸入時，混沌波形由混沌態變為大周期狀態，說明Duffing混沌系統具有一定的弱信號檢測特性。

根據Duffing混沌仿真電路設計，后期又制作了實際Duffing混沌電路板，進一步證明Duffing混沌系統弱信號檢測的可行性，對檢測領域的實際應用具有一定的參考價值。

3 結束語

利用Melnikov方法，對Duffing混沌弱信號檢測系統進行了理論分析。利用Matlab仿真軟件，分析了Duffing系統的相平面圖、時序、龐加萊、功率譜和分岔圖等系統特性以及系統對指數、高斯和瑞利不同包絡信號的敏感度。分析了白噪聲和色噪聲對系統的抗干擾性能，利用Multisim實現了電路仿真分析，設計制作了Duffing混沌電路板，并通過調試得到了較為理想的檢測性能。試驗結果對Duffing混沌弱信號檢測系統的實際工程應用具有促進作用。

[1] 聶春燕,徐振忠.混沌系統在弱信號檢測中的應用[J].傳感器與微系統，2003,22(1):55-57.

[2]ZHANGXY,GUOHX,WANGBH,etal.Anewmethodfordetectinglinespectrumofshipradiatednoiseusingduffingoscillator[J].ChineseScienceBulletin,2007,52(14): 1906-1912.[3]FUYQ,WUDM,ZHANGL,etal.AcircularzonepartitionmethodforidentifyingDuffingoscillatorstatetransitionanditsapplicationtoBPSKsignaldemodulation[J].ChinaInformationSciences,2011,54(6):1274-1282.

[4] 王冠宇,陳大軍,林建亞,等.Duffing振子微弱信號檢測方法的統計特性研究[J].電子學報,1998,26(10):38-44.

[5] 路鵬,李月.微弱正弦信號幅值混沌檢測的一種改進方案[J].電子學報,2005,33(3): 527-529.

[6] 聶春燕.混沌系統與弱信號檢測[M].北京:清華大學出版社,2009.

[7] 劉海波,吳德偉,戴傳金,等.基于Duffing振子的弱正弦信號檢測方法研究[J].電子學報,2013,41(1):8-12.

[8] 劉海波,吳德偉,金偉,等.Duffing振子微弱信號檢測方法研究[J].物理學報,2013,62(5):50-51.

[9] 聶春燕,石要武,衣文索,等.強噪聲下利用混沌系統測量頻率的新方法[J].傳感器與微系統，2004,23(3):57-59.

[10]LIUJM.Anewwaytogeneratehighdimensionalhyperchaos[J].JournalofComputers,2013,8(9):2348-2355.

[11]許喆,劉崇新,楊韜.一種新型混沌系統的分析及電路實現[J].物理學報,2010,59(1): 131-139.

Analysis and Circuit Implementation of the Duffing Chaotic Weak Signal Detection System

CAO Manting, SONG Feifei

(Key Lab of Industrial Computer Control Engineering of Hebei Province，Yanshan University, Qinhuangdao 066004, China)

The widespread used Duffing chaotic weak signal detection system are analysed by the Melnikov method.The numerical simulation analyses are been done by Matlab software.The circuit simulation analyses are been done by using Multisim software.The Duffing chaotic circuit board is designed and producted.The ideal detection performance has been gotten through the debugging.These verify that the Duffing chaotic weak signal detection system can be realized by electronic circuit.They has a role in promoting the Duffing chaotic weak signal detection system to the actual engineering application and has the high reference value for the further research in the field of weak signal detection of other chaotic signals.

Duffing system; Chaotic algorithm; Matlab; Noise immucnity; Gaussian distrtution; Rayleigh distribustion; Colored noise

曹滿婷(通信作者)，女，高級實驗師,主要從事計算機控制、混沌控制相關技術的研究及應用工作。E-mail:cat@ysu.edu.cn。

TH7;TP2

A

10686/j.cnki.issn 1000-0380.201701019

修改稿收到日期:2016-06-19