一種基于GSC的自適應和差測角方法

孔永飛，吳海洲

(中國電子科技集團公司第五十四研究所,河北 石家莊 050081)

一種基于GSC的自適應和差測角方法

孔永飛，吳海洲

(中國電子科技集團公司第五十四研究所,河北 石家莊 050081)

在陣列信號處理中，通常利用和差波束估計目標角度，存在干擾時自適應波束形成在干擾方向形成零陷、和差波束的主瓣方向圖產生畸變、和差波束比與普通波束形成存在偏差、角度估計結果誤差較大等問題。為解決上述問題，開展了無需校正的自適應和差波束測角研究，提出一種基于廣義旁瓣相消器的和差波束雙通道結構，該結構可以在抑制干擾的同時保持主瓣波束方向圖，角度估計結果精度高。仿真結果表明，提出的方法在有效抑制干擾的同時，保持了良好的單脈沖特性。

GSC；自適應和差波束；鑒角曲線

0 引言

在自適應陣列信號處理中，應用和差波束測角技術[1]時，如何在抑制干擾的同時減輕對和差波束主瓣方向圖的影響[2]，獲得良好的鑒角曲線，是一個值得研究的課題。

廣義旁瓣相消器(Generalized Side-lobe Canceller，GSC)的自適應干擾對消思想基于維納濾波原理，通過抵消上、下支路中的相關干擾和噪聲，輸出的誤差信號即為期望信號。文獻[3]提出一種快速自適應和差測角方法，基于GSC結構形成和差波束，其自適應輔助支路未做降維處理，運算復雜度較高。文獻[4]提出一種基于GSC結構的三通道自適應和差測角方法，在自適應輔助支路中，采用多級維納濾波器構造降維阻塞矩陣，方法復雜，運算量較大。

本文提出一種基于GSC的和差波束雙通道結構，在自適應輔助支路中，構造穩健降維阻塞矩陣，在保持和差波束主瓣方向圖的基礎上，形成干擾方向的零陷，應用對稱取反法[5]，利用和差波束估計目標角度。

1 對稱取反法

在N元線陣應用和差測角技術時，采用對稱取反法，將所有陣元等分為2個子陣，和波束通道與差波束通道的構成如圖1所示。

對應的和與差操作矢量如下：

利用和差操作矢量，得到普通波束形成和波束權矢量w∑及差波束權矢量wΔ:

w∑=a(θ0)○T∑,wΔ=a(θ0)○TΔ。

式中，θ0為波束指向角；○表示Hadamard乘積。

偏角Δθ的計算公式為：

式中，L0為子陣相位中心到對稱軸的距離。

圖1 和差波束構成示意

2 和差波束的GSC結構

基于GSC的和差波束雙通道結構如圖2所示，由2個并行的GSC構成，上GSC結構對應和波束通道，下GSC結構對應差波束通道。經GSC上下支路變換后，進入維納濾波器，通過抵消上、下支路中的相關干擾和噪聲，輸出的誤差信號即為和波束信號和差波束信號。

圖2 基于GSC的和差波束雙通道結構

和與差通道GSC權矢量如下：

(1)

在實際陣列應用中，為了減小由于通道誤差[6]造成的信號相消現象，對阻塞矩陣加以改進，通常把期望信號的理想導向矢量向信號子空間做投影[7]，利用投影導向矢量構成的降維阻塞矩陣比直接利用理想導向矢量構成的降維阻塞矩陣有更好的阻塞能力。

采用信號子空間和噪聲子空間特征向量的線性組合構造的阻塞矩陣BN×J，其中N表示陣元個數，J表示阻塞矩陣維數，只有當J=M-1時，M為目標信號個數與干擾信號個數之和，抗干擾后的和差波束主波束畸變較小，才能用于和差波束測角，現簡要分析如下：

當J=N-1時，阻塞矩陣為：

B=[b1b2…bN-1]N×(N-1)。

(2)

GSC結構權矢量一般形式如下：

(3)

(4)

又有

(5)

(6)

(7)

把式(7)代入式(3)，得到

(8)

由于子空間投影導向矢量ap與噪聲特征矢量矩陣En正交，可得

(9)

將式(9)代入式(8)，有

(10)

由此可得，在GSC結構中，自適應輔助支路采用N-1列穩健阻塞矩陣時，結果與穩健LCMV方法等效，由于穩健LCMV方法對指向誤差不敏感[8]，主瓣波束始終指向實際信號方向，不能用于和差波束角度估計。

實際上，在GSC結構中，白噪聲不可抵消，自適應輔助支路中只需包含干擾信號分量[9]，即利用信號子空間特征矢量的線性組合構造穩健降維阻塞矩陣BN×(M-1)，M由估計[10]得到，阻塞噪聲和期望信號，輔助支路只允許干擾信號通過，有效提高輸出信號的信干噪比，此時，自適應和方向圖可表示如下：

(11)

當a(θ)=a(θ0)時，由于B滿足

(12)

且B為信號子空間一組正交基的線性組合，滿足

(13)

由式(12)和式(13)，可得

(14)

把式(14)代入式(11)，當θ=θ0時，自適應和方向圖幅值為：

(15)

說明在θ0處的自適應波束形成方向圖與普通波束形成方向圖相同，且當θ在θ0附近時，a(θ)≈a(θ0)，BHa(θ)近似為0，主要是aH(θ0)a(θ)起作用，即自適應和波束形成在θ0附近接近于普通和波束形成。

自適應差方向圖可表示為：

(16)

式中，aH(θ0)為靜態差波束權矢量。同上，當θ=θ0時，有

(17)

同上，自適應差波束形成在θ0附近接近于普通差波束形成。

3 仿真驗證

以均勻線陣為例，陣元數N=32，陣元間距半波長，來波信號為遠場窄帶信號，且各信號互不相關，噪聲與來波信號也不相關。假定期望信號來自10°方位，信噪比為0dB，2個干擾信號分別來自40°和-10°，干噪比分別為30dB和20dB。

3.1 自適應和差波束方向圖

初始波束指向為11°，采樣點數為512，和差波束方向圖如圖3和圖4所示。

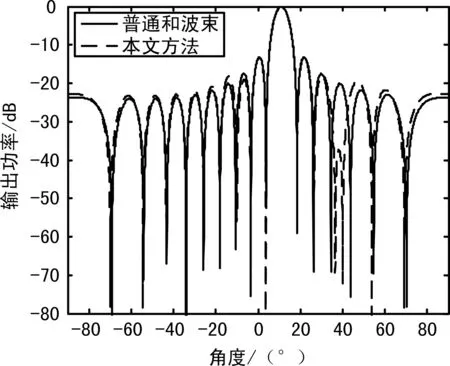
圖3 和波束方向圖

圖4 差波束方向圖

圖3是所提方法的自適應和波束方向圖與普通和波束形成方向圖，所提方法在干擾方向40°和-10°形成零陷，在40°方向零深-72.21dB，-10°方向零深-56.06dB，能有效地消除干擾。

圖4是所提算法的自適應差波束方向圖與普通差波束形成方向圖，所提方法在干擾方向40°和-10°形成零陷，在40°方向零深-61.35dB，-10°方向零深-63.37dB，能有效地消除干擾。

由圖3和圖4可知，本文所提方法形成的自適應和差波束的主瓣波束指向與普通波束的主瓣波束指向相同，同時有效抑制干擾。

所提方法的自適應單脈沖比曲線與普通和差波束的單脈沖比曲線如圖5所示。所提方法的單脈沖比曲線與靜態單脈沖比曲線十分接近，無需修正，利用該鑒角曲線得出角度估計結果為9.95°。

圖5 鑒角曲線

3.2 測角精度

其他仿真參數不變，采樣點數從256增加到4 096，分別做100次MonteCarlo實驗，角度估計結果如表1所示。

表1 不同采樣點數時角度估計結果

從表1可見，隨著采樣點數的增加，陣列協方差矩陣估計趨于理論值，所提方法測角結果均方根逐步減小，測角結果穩定性增高，相對于期望信號真實角度10°，即便在采樣點數較低時，誤差在0.2°以內，相對于主瓣波束寬度6.35°，誤差小于3.2%，隨著采樣點數的提高，誤差趨于1%，表明所提方法測角精度較高，無需修正鑒角曲線。

4 結束語

本文提出一種基于GSC結構的自適應和差波束形成的方法，可以在形成和差波束的同時在干擾方向形成零陷，得到良好的和差波束鑒角曲線，與普通和差波束鑒角曲線十分接近，測角精度較高，同時大大減少了GSC結構輔助支路自適應權的維數，降低了系統的運算量，在工程實踐中具有比較好的應用前景。仿真試驗及性能分析都驗證了算法的有效性和優越性。

[1] 胡體玲，李興國.單脈沖探測技術的發展綜述[J].現代雷達，2006，28(12)：24-29．

[2] 廖 暉，黃忠平.基于方向圖保形的單脈沖測角算法[J].中國電子科學研究院學報，2010，5(3)：301-304.

[3]MOONSH,HANDS,CHOMJ,etal.ANewGSCUsingMonopulseAngleEstimationTechniqueforFastTargetTracking[C]∥IEEEInternationalSymposiumonPhasedArraySystemsandTechnology,2003:158-163.

[4]HEYD,ZHOUJ,ZHOUBH.AdaptiveSumandDifferenceBeamformingforMonopulseSystemwithArrayAntennas[C]∥ 6thInternationalConferenceonWirelessCommunicationsNetworkingandMobileComputing(WiCOM),2010:1-5.

[5] 曾 操，陳 昊.相控陣子陣級和差多波束測角方法[J].西安電子科技大學學報，2007，5(3)：213-219.

[6] 見 偉，張 玉，韓名權.陣列天線通道誤差對波束性能的影響分析[J].無線電工程，2014，44(11)：45-48.

[7] 張濤麟，廖桂生，曾 操.基于廣義旁瓣相消的新降維方法[J].雷達科學與技術，2007，5(3)：213-219.

[8]FELDMANDD,GRIFFITHSLJ.AProjectionApprochforRobustAdaptiveBeamforming[J].IEEETransactionsonSignalProcessing,1994,42(4):867-876.

[9]VANVEENBD.EigenstructureBasedPartiallyAdaptiveArrayDesign[J].IEEETransactionsonAntennasandPropagation,1988,36(3):357-362.

[10] 貢彥飛.基于蓋爾圓準則的信源個數估計算法比較[J].無線電通信技術，2012，38(4)：57-59.

孔永飛 男，(1987—)，碩士，工程師。主要研究方向：航天測控、陣列信號處理。

吳海洲 男，(1977—)，博士，高級工程師。主要研究方向：航天測控、陣列信號處理。

An Angle Estimation Method by Adaptive Sum and Difference Beam-forming Based on GSC

KONG Yong-fei,WU Hai-zhou

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

In array signal processing,the angle of target is usually estimated by applying sum and difference beam-forming.Adaptive beam-forming distorts the sum and difference main lobe patterns,resulting in difference between the adaptive sum-difference ratio curve and the common sum-difference ratio curve,which leads to serious angle estimation error.An angle estimation algorithm without correction based on sum and difference beam-forming is proposed to solve the above problem.The proposed algorithm is based on the GSC structure of sum and difference channels,and has effective jamming suppression and high performance of angle estimation with less impact on sum-difference ratio.Simulation results demonstrate that the proposed algorithm can suppress jamming effectively,while preserving good monopulse performance.

GSC;adaptive sum and difference beam-forming;monopulse response curve

10.3969/j.issn.1003-3106.2017.01.09

孔永飛,吳海洲.一種基于GSC的自適應和差測角方法[J].無線電工程,2017,47(1):36-39.

2016-11-08

國家高技術研究發展計劃(“863”計劃)基金資助項目(2013AA122105)。

TTN911

A

1003-3106(2017)01-0036-04