定位于材料基因組計劃的鎳基高溫合金互擴散系數(shù)矩陣的高通量測定

湯 穎， 陳 娟， 杜 勇， 張利軍

(1.中南大學 粉末冶金國家重點實驗室，長沙 410083； 2. Thermo-Calc Software AB, Norra Stationsgatan 93, SE-113 64 Stockholm, Sweden)

定位于材料基因組計劃的鎳基高溫合金互擴散系數(shù)矩陣的高通量測定

湯 穎1,2， 陳 娟1， 杜 勇1， 張利軍1

(1.中南大學 粉末冶金國家重點實驗室，長沙 410083； 2. Thermo-Calc Software AB, Norra Stationsgatan 93, SE-113 64 Stockholm, Sweden)

尋找新一代鎳基單晶高溫合金中Re的替代元素以實現(xiàn)少Re甚至無Re化是當前高溫合金領(lǐng)域的研究熱點。從擴散系數(shù)角度出發(fā)尋找具有與Re相當或者更低擴散系數(shù)的元素是有效的研究策略之一。在多元合金中，互擴散系數(shù)矩陣可全面表征任一合金元素的擴散能力。因此，精確測定不同合金元素在鎳基高溫合金γ和γ′相中隨成分和溫度變化的互擴散系數(shù)矩陣是當務(wù)之急。首先，概述當前鎳基高溫合金互擴散系數(shù)矩陣測定的現(xiàn)狀，以及用于多元合金互擴散系數(shù)測定的傳統(tǒng)Matano-Kirkaldy方法和新型數(shù)值回歸方法。由于傳統(tǒng)Matano-Kirkaldy方法效率低，文獻中鮮有鎳基高溫合金三元及更高組元體系互擴散系數(shù)矩陣的報道。本研究小組最近基于Fick第二定律和原子移動性概念發(fā)展起來的新型數(shù)值回歸方法，可用于任意組元合金精準互擴散系數(shù)矩陣的高通量測定。隨后以Ni-Al-Ta三元合金γ相為例詳細闡述新型數(shù)值回歸法用于合金互擴散系數(shù)矩陣高通量測定以及測定結(jié)果的可靠性驗證過程。之后，簡述本研究小組關(guān)于鎳基高溫合金γ和γ′相互擴散系數(shù)矩陣測定的最新進展。目前已經(jīng)完成了核心三元合金體系Ni-Al-X(X=Rh, Ta, W, Re, Os和Ir) γ及γ'相互擴散系數(shù)矩陣的高通量測定，并對結(jié)果可靠性進行了細致的驗證。通過對比不同元素在鎳基高溫合金中的互擴散系數(shù)，初步提出新一代鎳基高溫合金中Re的可能替代元素及合金成分設(shè)計的關(guān)鍵。最后，指出鎳基高溫合金互擴散系數(shù)矩陣測定的下一步工作和互擴散系數(shù)矩陣高通量測定的發(fā)展方向。

鎳基高溫合金；互擴散系數(shù)；高通量；數(shù)值回歸方法；材料基因組

鎳基高溫合金具有良好的高溫強度、優(yōu)異的抗腐蝕性和抗氧化性，是目前航空發(fā)動機和燃氣渦輪葉片等高溫零部件的主要用材[1-2]。為了滿足高溫極限使用環(huán)境的要求，鎳基高溫合金需具備高的抗蠕變性能。一般情況下，合金的抗蠕變性能在一定程度上依賴于所添加合金元素的擴散系數(shù)，也就是說，添加具有較低擴散系數(shù)的合金元素可以有效地提高合金的抗蠕變性能。因而，工業(yè)上常常將具有較低擴散系數(shù)的難熔元素添加到Ni基高溫合金中以提高其抗蠕變性能[3]。從第二代鎳基單晶高溫合金開始，就加入具有極低擴散系數(shù)的稀土元素Re。Re的添加量從第二代鎳基單晶高溫合金中的3%(質(zhì)量分數(shù)，下同)增加到了第三代合金中的6%，并有進一步增加的趨勢[4]。盡管添加Re元素會在一定程度上提高鎳基高溫合金的抗蠕變性能，但也引入了一些問題，如：(1)Re的加入會形成有害的拓撲密排相(TCP相)，造成合金力學性能的嚴重降低；(2)Re的價格昂貴，增加了鎳基高溫合金的成本。因此，尋找新一代鎳基單晶高溫合金中Re的替代元素，以實現(xiàn)少Re甚至無Re化是當前高溫合金領(lǐng)域的研究熱點。

從擴散系數(shù)角度出發(fā)尋找具有與Re相當或者更低擴散系數(shù)的元素以部分或者完全替代Re元素是有效的研究策略之一。目前，已有研究者開展了相關(guān)工作[3,5-7]，這些報道大都采用第一原理計算不同合金元素在純鎳中的雜質(zhì)擴散系數(shù)。實際的鎳基高溫合金含10種以上合金元素，在服役過程中涉及各元素在不同相中隨成分和溫度變化的相互擴散系數(shù)。此外，第一原理計算結(jié)果依賴于已知的擴散機制，其可靠性仍需要一定實驗數(shù)據(jù)的驗證。因此，精確測定不同合金元素在鎳基高溫合金fcc(即：γ)和L12(即：γ′)相中隨成分和溫度變化的互擴散系數(shù)矩陣是當務(wù)之急。

迄今為止，文獻中僅有少數(shù)關(guān)于鎳基高溫合金二元子體系實測擴散系數(shù)的報道[8-10]，而三元及更高組元體系則幾乎未見報道，這主要與當前擴散系數(shù)的測定方法效率較低有關(guān)。在三元系中，單一物相的互擴散系數(shù)矩陣對應(yīng)有4個獨立的互擴散系數(shù)，包括2個主擴散系數(shù)和2個交叉擴散系數(shù)。對于三元系互擴散系數(shù)矩陣的測定，一般采用傳統(tǒng)的Matano-Kirkaldy(M-K)方法[11-13]與單相擴散偶技術(shù)相結(jié)合的方法。該方法要求必須有2組或以上的三元擴散偶，并且每2組擴散偶的擴散路徑上必須存在1個以上的交點。雖然M-K方法可以獲得交點處準確的互擴散系數(shù)，但一般制備2組擴散偶只能獲得1個交點處的互擴散系數(shù)矩陣。若采用M-K方法測定目標三元系隨成分和溫度變化的互擴散系數(shù)矩陣，需要精確設(shè)計大量的單相擴散偶，測定效率低。此外，由于很難設(shè)計在擴散路徑上具有交點的多元擴散偶，M-K方法幾乎未見應(yīng)用于更高元體系互擴散系數(shù)測定的報道。

為了提高三元互擴散系數(shù)的測定效率，國內(nèi)外科研工作者試圖通過單一的擴散偶獲取三元合金的互擴散系數(shù)，如Dayananda和Sohn[14]、Zhang等[15]、Jaques和Lacombe[16]以及Paul等[17]。這些方法或局限于平均擴散系數(shù)[14-16]或局限于偽二元系互擴散系數(shù)的計算[17]，仍無法高效獲得目標合金隨成分和溫度變化的互擴散系數(shù)矩陣[18]。2014年，本研究小組基于Fick第二定律和原子移動性概念發(fā)展了一種實用型數(shù)值回歸方法(pragmatic numerical inverse method)[19]，并實現(xiàn)了程序化。該方法的優(yōu)點在于：(1)可以獲得三元單一擴散偶沿整個擴散通道的互擴散系數(shù)；(2)可以方便地推廣到多元互擴散系數(shù)的計算。隨后，該方法成功應(yīng)用于Co合金[19]、無鉛焊料[20]、Al合金[21]三元系單相互擴散系數(shù)矩陣的測定。結(jié)果表明：(1) 采用該實用型數(shù)值回歸法所測定的互擴散系數(shù)與傳統(tǒng)的M-K方法得到的結(jié)果吻合；(2) 該方法適用于不同類型成分-距離曲線的互擴散系數(shù)測定，包含對稱型、非對稱型及含有零通量面型等等。最近，本研究小組從以下四個方面進一步增強了該數(shù)值回歸方法[22]：(1)采用一套參數(shù)用于同一溫度多組擴散偶隨成分變化互擴散系數(shù)矩陣的測定；(2)證實了在簡單相中是否采用精準的熱力學因子對所獲得互擴散系數(shù)矩陣可靠性的影響可以忽略；(3)引入互擴散通量作為誤差最小化的另一條件，提高數(shù)值收斂性；(4)將該方法拓展到可適用于任意組元(即從二元、三元到多元)單相合金互擴散系數(shù)矩陣的測定。因此，該新型數(shù)值回歸方法可用于鎳基高溫合金γ和γ′相精準互擴散系數(shù)矩陣的高通量測定，而且通過對比各合金元素互擴散系數(shù)的大小可高效尋找新一代鎳基單晶高溫合金中Re可能的替代元素。此外，該新型數(shù)值回歸方法完全符合當前“材料基因組”(Materials Genome Initiative,MGI)計劃的高效特征，可作為MGI計劃重要的組成部分，用于目標合金互擴散系數(shù)高效數(shù)據(jù)庫的建立，加快新型合金的設(shè)計及開發(fā)。

本文首先簡單介紹用于互擴散系數(shù)測定的傳統(tǒng)M-K方法以及新型數(shù)值回歸方法，隨后以Ni-Al-Ta三元系為例詳細闡述新型數(shù)值回歸法用于γ相精準互擴散系數(shù)矩陣的高效測定過程及其測定結(jié)果可靠性的驗證。第3節(jié)將簡述本研究小組關(guān)于鎳基高溫合金核心三元系Ni-Al-X(X=Rh, Ta, W, Re, Os) γ和γ′相互擴散系數(shù)矩陣測定的最新進展。通過互擴散系數(shù)的詳細對比，初步提出了新一代鎳基高溫合金中Re的可能替代元素。最后，指出了鎳基高溫合金互擴散系數(shù)測定的下一步工作，以及互擴散系數(shù)高通量測定的發(fā)展方向。

1 互擴散系數(shù)的測定方法

1.1 傳統(tǒng)的Matano-Kirkaldy方法

對于A-B-C三元系，如假定組元C為溶劑元素，A和B為溶質(zhì)元素，其Fick第一定律可表述為：

(1)

(2)

(3)

在三元系中，一組擴散偶可以得到兩組上述方程(即：式(1)至式(3))，但不足以得到4個獨立的擴散系數(shù)。因此，Kirkaldy[11-13]提出可設(shè)計2組三元擴散偶，且該2組擴散偶的擴散通道上必須存在至少一個交點。在該交點處，則有4組上述方程，就可以計算出該三元系在交點成分處的4個擴散系數(shù)。這就是傳統(tǒng)的Matano-Kirkaldy方法。

1.2 新型數(shù)值回歸方法

在上述同樣的三元系中，F(xiàn)ick第二定律的表達式為：

(4)

(5)

(6)

式中：μi表示組元i的化學勢?？蓮南鄳?yīng)體系精確的熱力學描述(如采用CALPHAD方法建立的熱力學數(shù)據(jù)庫[26])中得到可靠的熱力學因子。需要指出的是，本研究小組Chen等[22]最近證實了對于缺乏精準熱力學描述的簡單相而言，采用新型數(shù)值回歸方法仍可獲得可靠的互擴散系數(shù)矩陣。

式(5)中原子移動性參數(shù)Mi則可參照Andersson and Gren[27]提出的公式(7)來獲得。

(7)

由式(7)可知，Mi直接與ΔGi相關(guān)。一般來說，參數(shù)ΔGi與合金的成分、溫度和壓力相關(guān)，其表達式可以用Redlich-Kister多項式展開得到:

(8)

聯(lián)立式(4)到式(8)，可以模擬給定擴散偶在一定擴散時間后的成分-距離(Fick第二定律)及互擴散通量(Fick第一定律)曲線。根據(jù)本研究小組Chen等的工作[19,22], 將模擬的成分-距離和互擴散通量-距離曲線值與實驗測定的成分-距離和互擴散通量-距離曲線值的差值作為優(yōu)化對象，運用迭代方法進行優(yōu)化，當兩者之間的差別最小時，則認為該組參數(shù)最合理，即：

(9)

(10)

(11)

(12)

1.3 誤差評估方法

我們采用Lechelle等[29]提出的科學方法來評估互擴散系數(shù)的誤差。該方法基于誤差傳遞思想。在互擴散系數(shù)的計算過程中，每一項的誤差均可用下式表示：

(13)

式中：A，B…是方程f的相關(guān)變量；u(α) (α=A,B...)為α(如：濃度、Matano平面等)的誤差。

2 代表性合金Ni-Al-Ta體系γ相互擴散系數(shù)矩陣的高效測定

本節(jié)將以本研究小組剛發(fā)表的Ni-Al-Ta三元合金γ相為例[30]，詳細闡述新型數(shù)值回歸法應(yīng)用于合金互擴散系數(shù)矩陣高通量測定的過程。同時我們也將討論如何驗證所測定結(jié)果的可靠性。

2.1 實驗過程

采用純度均為99.99%的Ni、Al和Ta作為原材料，在WKDHL非自耗電弧熔煉爐(WK-I，Opto-electronics Co., Ltd., Beijing)中及高純氬氣氛保護下熔煉，各合金名義成分如表1所示。為使難熔元素Ta能完全融入合金中，保證合金的均勻性，按照前期工作的三步法進行熔煉[9]。由于熔煉過程原料的熔損很小，不需進一步的合金成分分析。隨后將熔煉好的合金真空封入石英管中，并置于高溫管式爐中，均勻化退火48 h，以進一步提高合金均勻性并增加晶粒尺寸以減小界面短程擴散的影響。接著，將退火后的合金切成5 mm×5 mm×1 mm的小塊，經(jīng)打磨和拋光后，將兩塊組成擴散偶的合金緊密貼合放入鉬夾具中制成擴散偶。所制備的9組擴散偶如表1所示。將制備好的擴散偶封入石英管并放入高溫管式爐中進行擴散退火。9組擴散偶的不同退火機制也列入表1中。隨后將石英管從爐膛中快速取出，并立即水淬。對所有擴散退火后的樣品沿擴散方向的平行面進行拋光。最后，采用電子探針EPMA(日本電子生產(chǎn)，型號為JXA-8100)對這9組擴散偶沿擴散方向平行面的成分進行檢測，測定其成分-距離曲線。成分測定在進行原子序數(shù)校正、吸收校正和熒光校正后與標樣的對比得出，測量誤差為1%～3%。

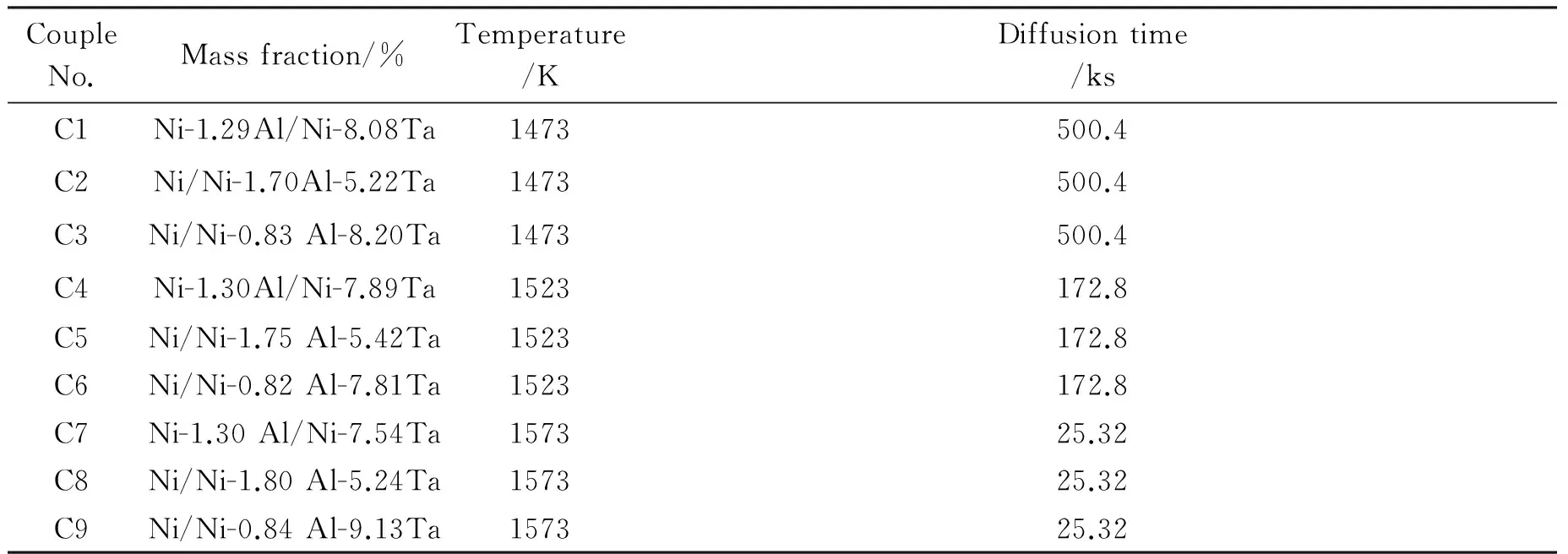
表1 設(shè)計的fcc Ni-Al-Ta體系9組擴散偶及其端際合金名義成分[30]

2.2 γ相互擴散系數(shù)的高效測定及可靠性驗證

采用EPMA測定的成分-距離曲線如圖1所示。由于篇幅限制，這里只給出了具有代表性的C7，C8和C9擴散偶在1300 ℃擴散退火7 h的成分-距離曲線(圖中符號代表實驗點)?；谒鶞y擴散偶不同組元的成分-距離曲線，根據(jù)公式(2)和(3)可以獲得相應(yīng)的互擴散通量(圖中符號代表實驗點)，也如圖1所示。從圖1中可以發(fā)現(xiàn)，Ni-Al/Ni-Ta類型的擴散偶中Ni的成分距離曲線呈現(xiàn)N型(如圖1(a))，而Ni/Ni-Al-Ta類型的擴散偶中Ni的成分距離曲線呈現(xiàn)S型(如圖1(b)和(c))。

進行對比。從圖中4可以看出，由三元主擴散系數(shù)外推得到的值與Ni-Al和Ni-Ta二元互擴散系數(shù)的實驗值符合得很好。這進一步驗證所計算得到互擴散系數(shù)的可靠性。

表2 基于傳統(tǒng)M-K方法和新型數(shù)值回歸法得到的Ni-Al-Ta合金γ相互擴散系數(shù)的對比[30]

3 鎳基高溫合金互擴散系數(shù)矩陣測定的最新進展及Re的可能替代元素

最近，本研究小組陳娟在博士論文中采用與上述Ni-Al-Ta三元系相同的方法高通量地測定了Ni-Al-X(X=Rh, Ta, W, Re, Os和Ir)系列三元系在1373～1573 K下γ和γ′相的互擴散系數(shù)矩陣[32]。通過與傳統(tǒng)M-K方法計算結(jié)果、文獻報道的邊際二元系互擴散系數(shù)以及實測成分-距離和互擴散通量曲線的對比，驗證了新型數(shù)值回歸方法得到的鎳基高溫合金γ和γ′相互擴散系數(shù)矩陣的可靠性。本節(jié)將基于陳娟的實測結(jié)果[32]，通過詳細對比不同元素在鎳基高溫合金γ和γ′相中的互擴散系數(shù)大小來嘗試尋找新一代鎳基高溫合金中Re的可能替代元素。

4 結(jié)論及展望

綜上，新型數(shù)值回歸法與單相擴散偶的結(jié)合為鎳基高溫合金互擴散系數(shù)矩陣的高通量測定提供了一種行之有效的方法。當前，本研究小組已經(jīng)完成了鎳基高溫合金核心三元合金體系Ni-Al-X(X=Rh, Ta, W, Re, Os和Ir) γ及γ′相互擴散系數(shù)矩陣的高通量測定，并對結(jié)果可靠性進行了細致的驗證。基于對不同元素在鎳基高溫合金中互擴散系數(shù)的對比，初步提出了在新一代的鎳基高溫合金成分設(shè)計中將Os作為鎳基高溫合金中Re的可能替代元素，而且可將W元素應(yīng)盡可能多的分配在γ′相中。

接下來本研究小組將擴大所研究的添加元素范圍，而且通過高通量測定更高元體系乃至實際合金體系的互擴散系數(shù)矩陣，為新一代單晶鎳基高溫合金的無Re和少Re化以及精準的成分設(shè)計打下堅實的基礎(chǔ)。

此外，除了在互擴散系數(shù)的計算方法外，還將通過對實驗技術(shù)的改進來進一步提高多元合金互擴散系數(shù)矩陣的測定效率。如將Zhao等[35-36]提出的多元擴散節(jié)與新型數(shù)值回歸方法結(jié)合來進一步提高互擴散系數(shù)矩陣的測定效率，實現(xiàn)互擴散系數(shù)矩陣更高效的高通量測定。

(責任編輯：張 崢)

MGI-oriented High-throughput Measurement of Interdiffusion Coefficient Matrices in Ni-based Superalloys

TANG Ying1,2, CHEN Juan1, DU Yong1, ZHANG Lijun1

(1.State key laboratory of Powder Metallurgy, Central South University, Changsha 410083, China; 2.Thermo-Calc Software AB, Norra Stationsgatan 93, SE-113 64 Stockholm, Sweden)

One of the research hotspots in the field of high-temperature alloys was to search the substitutional elements for Re in order to prepare the single-crystal Ni-based superalloys with less or even no Re addition. To find the elements with similar or even lower diffusion coefficients in comparison with that of Re was one of the effective strategies. In multicomponent alloys, the interdiffusivity matrix were used to comprehensively characterize the diffusion ability of any alloying elements. Therefore, accurate determination of the composition-dependant and temperature-dependent interdiffusivities matrices of different elements in γ and γ′ phases of Ni-based superalloys was high priority. The paper briefly introduces of the status of the interdiffusivity matrices determination in Ni-based superalloys, and the methods for determining the interdiffusivities in multicomponent alloys, including the traditional Matano-Kirkaldy method and recently proposed numerical inverse method. Because the traditional Matano-Kirkaldy method is of low efficiency, the experimental reports on interdiffusivity matrices in ternary and higher order sub-systems of the Ni-based superalloys were very scarce in the literature. While the numerical inverse method newly proposed in our research group based on Fick′s second law can be utilized for high-throughput measurement of accurate interdiffusivity matrices in alloys with any number of components. After that, the successful application of the numerical inverse method in the high-throughput measurement of interdiffusivity matrices in alloys is demonstrated in fcc (γ) phase of the ternary Ni-Al-Ta system. Moreover, the validation of the resulting composition-dependant and temperature-dependent interdiffusivity matrices is also comprehensively made. Then, this paper summarizes the recent progress in the measurement of interdiffusivity matrices in γ and γ′ phases of a series of core ternary Ni-based superalloys achieved in our research group. Up to now, the interdiffusivity matrices in γ and γ′ phases of the core ternary systems including Ni-Al-X(X=Rh, Ta, W, Re, Os and Ir) have been efficiently measured, and their reliability has also been carefully validated. Based on the experimental results, the interdiffusivities for different elements in Ni-based superalloys are carefully compared, from which the potential substitutional alloying elements for Re in Ni-based supperalloys as well as the points for alloy composition design are proposed. Finally, the research work of next step on the measurement of interdiffusivity matrices in Ni-based superalloys as well as the development trends of high-throughput measurement of interdiffusivities in our research group are pointed out.

Ni-based superalloys; interdiffusion coefficient; high throughput; numerical inverse method; materials genome initiative

2016-10-17；

2016-10-30

國家自然科學基金項目(51301208)；湖南省自然科學基金項目(2015JJ3146);中南大學粉末冶金國家重點實驗室項目資助

張利軍(1983—)，男，博士，教授，主要從事合金熱力學、擴散動力學、微結(jié)構(gòu)及合金設(shè)計等領(lǐng)域研究，(E-mail)lijun.zhang@csu.edu.cn。

10.11868/j.issn.1005-5053.2016.100003

TB30；TG146.1

A

1005-5053(2017)01-0026-10