提高雷達(dá)數(shù)據(jù)利用率方法研究*

王 艦 李艷芳 吳海東

(中國洛陽電子裝備試驗中心 洛陽 471003)

?

提高雷達(dá)數(shù)據(jù)利用率方法研究*

王 艦 李艷芳 吳海東

(中國洛陽電子裝備試驗中心 洛陽 471003)

論文對影響雷達(dá)測量數(shù)據(jù)準(zhǔn)確性的因素進(jìn)行了分析探討。從多普勒頻移和天線旁瓣、雜波分析入手,結(jié)合公式推導(dǎo)和分析,得到影響雷達(dá)性能的變量和參數(shù),利用仿真軟件對其進(jìn)行模擬,推算出最優(yōu)的參數(shù)配置,為修正數(shù)據(jù)誤差和跳變提供了有效的參考。

雷達(dá)數(shù)據(jù); 多普勒頻移; 雜波; 旁瓣

Class Number TN958.4

1 引言

在以往處理的雷達(dá)數(shù)據(jù)中,經(jīng)常出現(xiàn)在一個航次內(nèi)大部分?jǐn)?shù)據(jù)變化平穩(wěn)而少部分?jǐn)?shù)據(jù)發(fā)生跳變的情況,導(dǎo)致數(shù)據(jù)無法使用,如圖1所示,而發(fā)生跳變的時間段內(nèi)的數(shù)據(jù),正是用戶想使用的真值。為提高雷達(dá)數(shù)據(jù)的利用率,本文從雷達(dá)信號形式入手分析了產(chǎn)生數(shù)據(jù)跳變的原因,給出了消除方法,進(jìn)而提高了數(shù)據(jù)的利用率。

2 多普勒頻移、天線旁瓣與雜波之間的關(guān)系

根據(jù)多次數(shù)據(jù)分析,造成圖1所示數(shù)據(jù)變化的原因是由于雷達(dá)回波信號異常引起的,在實際測量過程中,由于雷達(dá)常年使用,元器件老化,影響其法門、重復(fù)頻率、頻率間隔等指標(biāo),造成測量數(shù)據(jù)的誤差或跳變。造成這種數(shù)據(jù)變化的原因主要有兩個方面[1]:一是發(fā)射信號沒有達(dá)到標(biāo)準(zhǔn)的信號樣式,存在主信號和旁瓣差別不大的現(xiàn)象;二是接收機(jī)靈敏度下降,接受信號頻率偏差過大,致使部分真值信號不能通過接受濾波,過多的雜波信號通過,對數(shù)據(jù)造成影響。本文主要研究頻率偏移和雷達(dá)雜波對數(shù)據(jù)真值的影響。

2.1 雷達(dá)多普勒頻移

雷達(dá)工作體制為單脈沖,雷達(dá)發(fā)射脈沖信號遇到運動目標(biāo)時,產(chǎn)生回波,當(dāng)目標(biāo)和雷達(dá)之間有相對徑向運動vr,雷達(dá)接收到的回波信號頻率fs會和雷達(dá)發(fā)射頻率f0之間會產(chǎn)生一個頻率差,且產(chǎn)生一個附加的多普勒脈沖信號,通過對該脈沖多普勒信號的分析,就可以確定運動目標(biāo)的速度、距離等分量值[2～3]。

圖2 多普勒 頻移示意圖

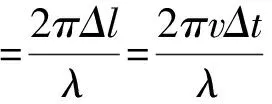
由上式fd計算可以看出,多普勒頻移與移動目標(biāo)速度及目標(biāo)移動方向,與無線信號入射方向之間的夾角有關(guān)。若目標(biāo)朝向入射波方向,則多普勒頻移為正,即接收頻率上升,反之下降。信號經(jīng)不同方向傳播和反射回波,其多徑分量造成接收機(jī)信號的多普勒擴(kuò)散,增加了信號帶寬。

2.2 雷達(dá)旁瓣和雜波

當(dāng)雜波和運動目標(biāo)回波在雷達(dá)顯示器上同時顯示時,會使目標(biāo)的觀測變得很困難[5]。如果目標(biāo)處在雜波背景內(nèi),弱的目標(biāo)淹沒在強(qiáng)雜波中,特別是當(dāng)雜波使接受系統(tǒng)產(chǎn)生過載時,發(fā)現(xiàn)目標(biāo)十分困難。目標(biāo)不在雜波背景內(nèi)時,要在成片雜波中很快分辨出運動目標(biāo)回波也不容易。精測雷達(dá)在跟蹤過程中,可能由于雜波過多丟失目標(biāo),也會因為突然的雜波信號增大,引起測量數(shù)據(jù)跳變。

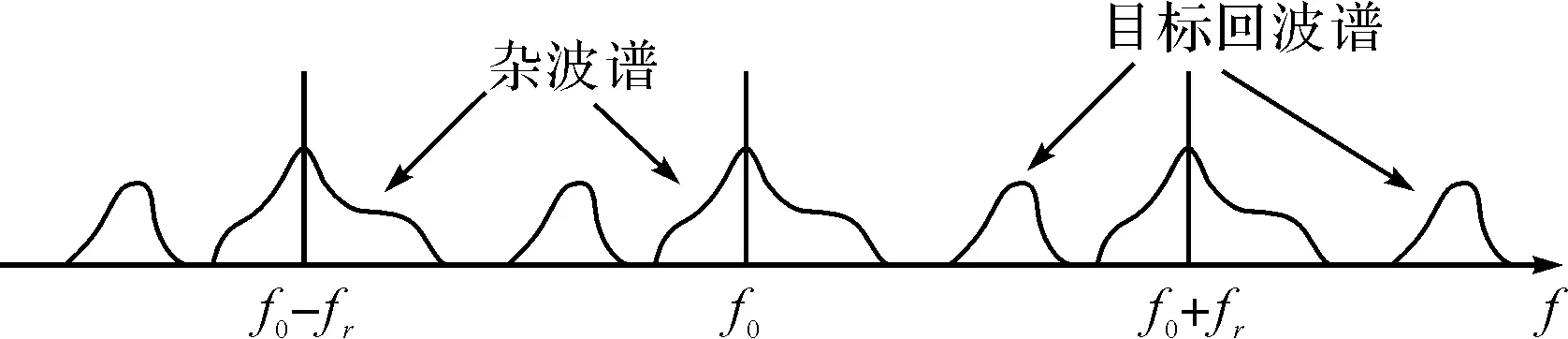
圖3 回波和雜波示意圖

通常背景雜波是頻域-時域分布相當(dāng)寬廣且功率相當(dāng)強(qiáng)的信號自身雜波,被稱之為脈沖多普勒雜波,其雜波頻譜是多普勒頻率-距離的函數(shù)[6],雜波頻譜的形狀和強(qiáng)度決定著雷達(dá)對具有不同多普勒頻率的目標(biāo)的檢測能力。

圖4 回波旁瓣示意圖

由于多普勒頻移可以有效限制雜波信號,所以在脈沖信號帶寬和重復(fù)頻率許可范圍內(nèi),可適當(dāng)調(diào)整濾波器,來提高雷達(dá)測量數(shù)據(jù)的精度。

2.3 多普勒頻移、天線旁瓣對雷達(dá)數(shù)據(jù)影響的分析

圖5 天線幾何 關(guān)系圖

實際雷達(dá)跟蹤過程中,目標(biāo)存在為一個三維空間,假設(shè)天線位置與目標(biāo)的幾何關(guān)系如圖5所示,飛機(jī)高度為h,速度為v,沿X軸方向飛行。圖中俯角為α,方位角為β,目標(biāo)附近的分辨單元內(nèi)雜波強(qiáng)度為Pc(α,β),則:

(1)

式中:P表示雷達(dá)峰值功率,G(α,β)為天線的增益,λ為雷達(dá)工作波長,σc為反射雜波截面積,Lc為系統(tǒng)對雜波的損耗,R雜波至雷達(dá)的斜距。R=h/sinα,h為目標(biāo)高度

σc=σ0ΔAc

(2)

σ0為雜波在P點的散射系數(shù),ΔAc為雜波面積。為方便起見,取雜波的后向散射系數(shù)模型為γ模型,則

σ0=γ0sinα

(3)

在點P處的多普勒頻移fd為:fd=(2/λ)Vcosαcosβ,對β微分(由于面積計算是以斜距環(huán)為單元的,因此不對α微分)

dfd=-(2/λ)Vcosαcosβ

dβ=dfd/|(2/λ)Vcosαcosβ|

(4)

由以上分析可得,在雜波分辨單元內(nèi)dRdβ占據(jù)的面積ΔAc為

ΔAc=RdRdβ

(5)

dR為距離向展寬。

將式(2)～(5)代入式(1),得

(6)

從式(6)可以清楚地看出雜波回波強(qiáng)度與雷達(dá)參數(shù)的關(guān)系。當(dāng)系統(tǒng)參數(shù)取定之后,雜波回波強(qiáng)度與天線增益的關(guān)系如式(7)所示。

(7)

由式(7)可知,俯仰角α越小雜波越強(qiáng),β越小即越靠近X軸區(qū)域,雜波也越大。為了減小這些地區(qū)的雜波,使得來自各個方向的雜波回波強(qiáng)度相近,唯一的方法是下式成立:

(8)

(9)

即所有落入dR、df單元內(nèi)的雜波強(qiáng)度相同。由此可得,在距離分辨單元ΔR和多普勒分辨單元Δfd內(nèi)的雜波強(qiáng)度為

(10)

由于雷達(dá)所采用的重復(fù)頻率會使回波存在距離域和多普勒頻率重疊,因此考慮真正落入一個分辨單元內(nèi)的雜波強(qiáng)度時必須計算重疊效應(yīng)。

令重復(fù)頻率為fr,則信號能分辨的距離為Rr=C/2fr,C為光速。因此信號接收的重疊次數(shù)為

M=int[(Rmax-h)/Rr]+1

(11)

由于每個距離環(huán)內(nèi)雜波多普勒展寬不一致,因此每個環(huán)要分開考慮。

令第i個環(huán)的斜距為:Rri=R1+(i-1)Rr;R1=Rmod(Rr)+KRrK的選擇是使h≤R1≤h+Rr。

對應(yīng)的俯仰角α=arcsin(h/Rri),該環(huán)內(nèi)的多普勒展寬為4Vcosα/λ=4V[1-(h/Rri)2]1/2/λ,則距離環(huán)內(nèi)的雜波在多普勒域的重疊次數(shù)N(i)為

N(i)=int{4V[1-(h/Rri)2]1/2/λfr}+1

(12)

又當(dāng)4Vcosα/λ≤Δfd時,式(10)中的Δfd應(yīng)修正為Δfd(i):

總之,落入一個分辨單元內(nèi)的雜波強(qiáng)度為

(13)

而信號回波功率為

(14)

(15)

又

(16)

將式(16)代入式(15)并整理可得:

(17)

即

(18)

從式(18)可以看出,與多普勒頻移相關(guān)的參數(shù)ΔR、信號旁瓣、天線增益(S/N)min都對雷達(dá)接收到得數(shù)據(jù)產(chǎn)生影響,也就是對數(shù)據(jù)精度產(chǎn)生影響。

3 仿真實驗及分析

根據(jù)上面的公式,為調(diào)整其中的參數(shù),得到最好的測量數(shù)據(jù)結(jié)果,利用與雷達(dá)對應(yīng)的仿真軟件對各個參數(shù)進(jìn)行測試和調(diào)整[7～8]。仿真程序中產(chǎn)生的信號樣式為原來雷達(dá)的信號樣式;脈沖數(shù)目、脈沖寬度、信號帶寬和脈沖重復(fù)周期均與原雷達(dá)信號一致;信號頻率為原雷達(dá)信號的中心頻率;信號的仿真是將實時模擬的信號頻譜作為雷達(dá)發(fā)射和回波的頻譜[9～10],然后利用信號幅度分布模型,按照相關(guān)發(fā)射信號和接收信號仿真的方法生成相關(guān)隨機(jī)序列。

通過不斷地進(jìn)行參數(shù)設(shè)置和配置、仿真模擬測量,并與原始測量數(shù)據(jù)進(jìn)行比對和校正,最終得到調(diào)整后的參數(shù),根據(jù)這些理論參數(shù)調(diào)整和更換雷達(dá)的元器件,確保雷達(dá)的測量數(shù)據(jù)盡可能精確。

圖6表示的是修改部分參數(shù)后,應(yīng)用仿真模擬軟件進(jìn)行仿真測量的結(jié)果,從圖上可以看出,測量數(shù)據(jù)相比較未調(diào)整前改善很多。圖7表示更換部分元器件及調(diào)整雷達(dá)參數(shù)后,對相同機(jī)型的測量數(shù)據(jù)的折線圖,可以看到,調(diào)整后,在幾個航次內(nèi),測量數(shù)據(jù)基本都保持了穩(wěn)定。

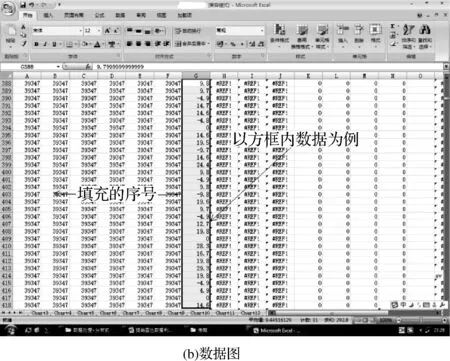
圖6 修改參數(shù)后的仿真數(shù)據(jù)示意圖

4 結(jié)語

本文從雷達(dá)真值數(shù)據(jù)的變化,分析雷達(dá)在測量過程中可能存在的影響真值的因素,重點研究了雷達(dá)回波所受的影響,在探討多普勒頻移和天線旁瓣回波影響的基礎(chǔ)上,通過公式分析與推導(dǎo),得到影響雷達(dá)性能的變量和參數(shù),可以為雷達(dá)改造和更換元器件提供參考。改變這些參量,可以在一定程度上提高雷達(dá)數(shù)據(jù)的精確率,避免出現(xiàn)數(shù)據(jù)誤差和跳變。

[1] Tadeusz Grabowski, Jan Dziupiński. Selected problems of processing a radar signal with a LFM-FSK modulation[J]. Aviation,2015,19(1):25-30.

[2] 蔡征宇,陳文斌.提高多普勒雷達(dá)測速估計精度的方法[J].南京理工大學(xué)學(xué)報,2009,33(3):520-523. CAI Zhengyu, CHEN Wenbin. Estimation Precision Improvement Method of Velocity Measurement for Doppler Radar[J]. Journal of Nanjing University of Science and Technology(Natural Science),2009,33(3):520-523.

[3] 李攀.多普勒頻移對脈沖壓縮雷達(dá)的影響及其補(bǔ)償研究[D].武漢:華中科技大學(xué),2007:12-13. LI Pan. Study of Dopper Effects on Pulse Compression Radar and the Dopper Compensation[D]. Wuhan: Huazhong University of Science and Technology,2007:12-13.

[4] Harsimranjit Kaur, Gaurav Soni. Performance Analysis of Free Space Optical Communication Link Using Different Modulation and Wavelength[J]. Journal of Scientific Research and Reports,2015,6(3):201-209.

[5] 俞根苗,方志紅.Dechirp及頻譜分析技術(shù)的目標(biāo)分辨率分析[J].雷達(dá)與對抗,2003(1):8-12. YU Genmiao, FANG Zhihong. Analysis of Resolution of Dechirp and Spectral Analysis Technology[J]. RADAR & ECM,2003(1):8-12.

[6] 徐克圣,程時兵.脈沖雷達(dá)精度校飛試驗仿真[J].大連交通大學(xué)學(xué)報,2009,30(3):83-86. XU Kesheng, CHENG Shibing. Simulation of the Accuracy of Pulse Radar in Flight Test[J]. Journal of Dalian Jiaotong University,2009,30(3):83-86.

[7] Bassem R. Mahafza. Radar Systerms Analysis and Design Using MATLAB. Second Edition[M]. Taylor & Francis Group,2012.

[8] 商臨峰,邢科義,甘友誼.信標(biāo)模式機(jī)動目標(biāo)跟蹤數(shù)據(jù)實實時時處理[J].控制理論與應(yīng)用,2012,29(1):59-64. SHANG Linfeng, XING Keyi, GAN Youyi. Real-time Processing of Tracking Data of Maneuvering Target in Beacon-mode[J]. Control Theory & Applications,2012,29(1):59-64.

[9] Markus Kock, Sebastian Hesselbarth, Martin Pfitzner. Hardware-accelerated design space exploration framework for communication systems[J]. Analog Integrated Circuits and Signal Processing,2014,78(3):557-571.

[10] Jianfeng Li, Xiaofei Zhang. Unitary Subspace-Based Method for Angle Estimation in Bistatic MIMO Radar[J]. Circuits, Systems, and Signal Processing,2014,33(2):501-513.

A Method to Increasing the Utilization Ration of the Radar Data

WANG Jian LI Yanfang WU Haidong

(China Electronic Equipment Testing Center, Luoyang 471003)

This paper dissects the factor that influences the accuracy of radar data. Doppler frequency shift, antenna sidelobe and radar clutter are the primarily elements. The correlation formula is deduced and some parameters and quantities that influence radar function are gotten. Finally, the superior parameters making use of simulation program of radar are estimated. These parameters can provide an available reference to avoid the data error and fluctuation.

radar data, doppler frequency shift, radar clutter, sidelobe

2016年7月11日,

2016年8月27日

王艦,男,碩士,工程師,研究方向:通信和信號處理。李艷芳,女,碩士,工程師,研究方向:數(shù)據(jù)處理。吳海東,男,碩士,工程師,研究方向:雷達(dá)工程。

TN958.4

10.3969/j.issn.1672-9722.2017.01.016