神奇的楊輝三角
2017-02-06 06:05:09劉彥永
數理化解題研究
2017年34期
關鍵詞:數學
劉彥永
(東北師大附中 130021)
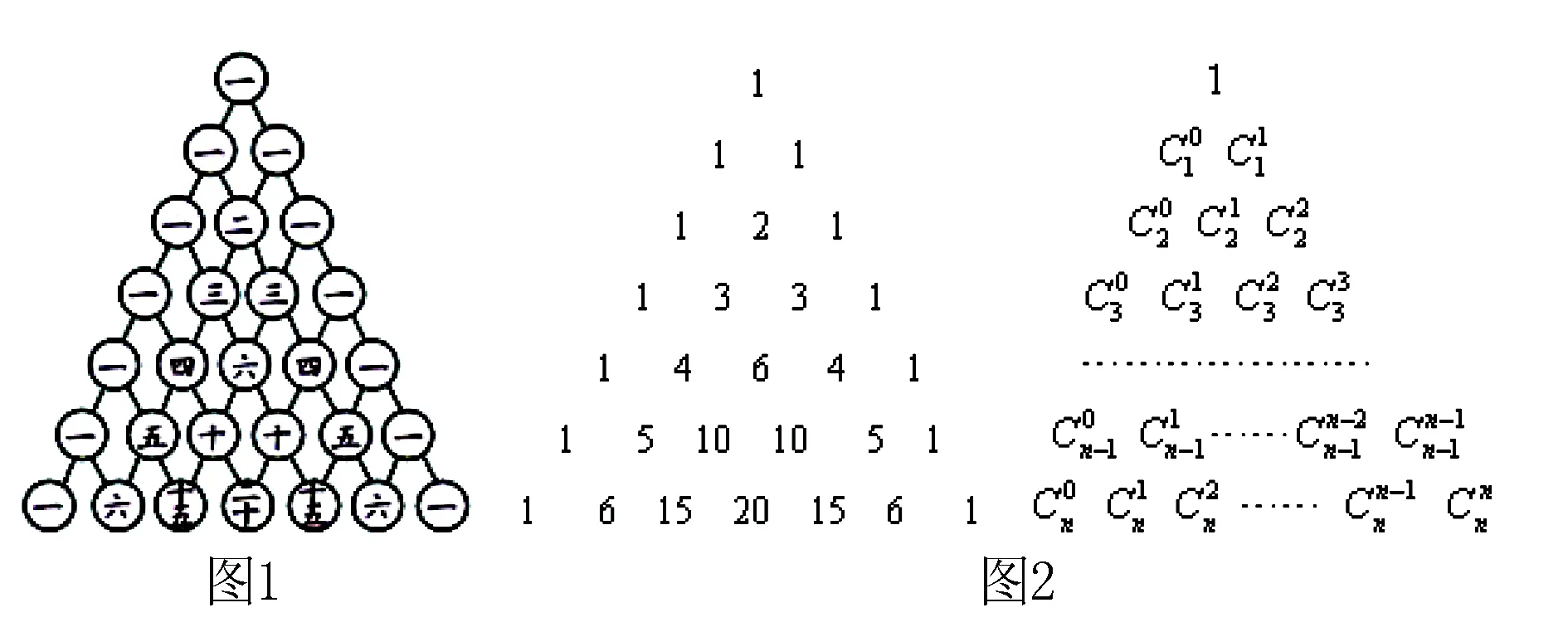
南宋的楊輝在他1261年所著的《詳解九章算法》一書中記錄了圖1所示的三角形數表,稱之為“開方作法本源”圖,即現在的楊輝三角,其本質是二項式系數在三角形中的一種幾何排列(如圖2).楊輝三角中蘊含著許多奇妙的性質,也與許多數學問題有著密切的聯系.古今中外,有許多數學家如賈憲、朱世杰、帕斯卡、華羅庚等都層深入研究過楊輝三角,下面我們一起走近楊輝三角吧.
一、楊輝三角與組合數
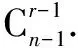
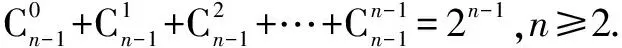
(5)每一行奇數位上的數的和與偶數位上的數的和相等,即
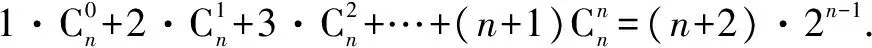
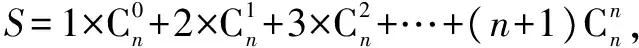
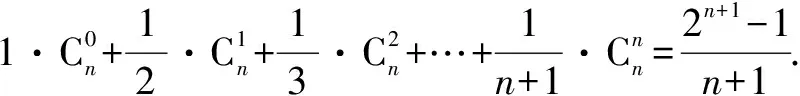
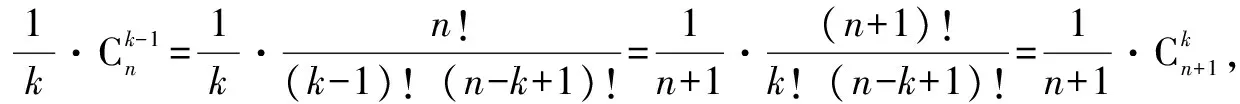

二、楊輝三角與概率問題
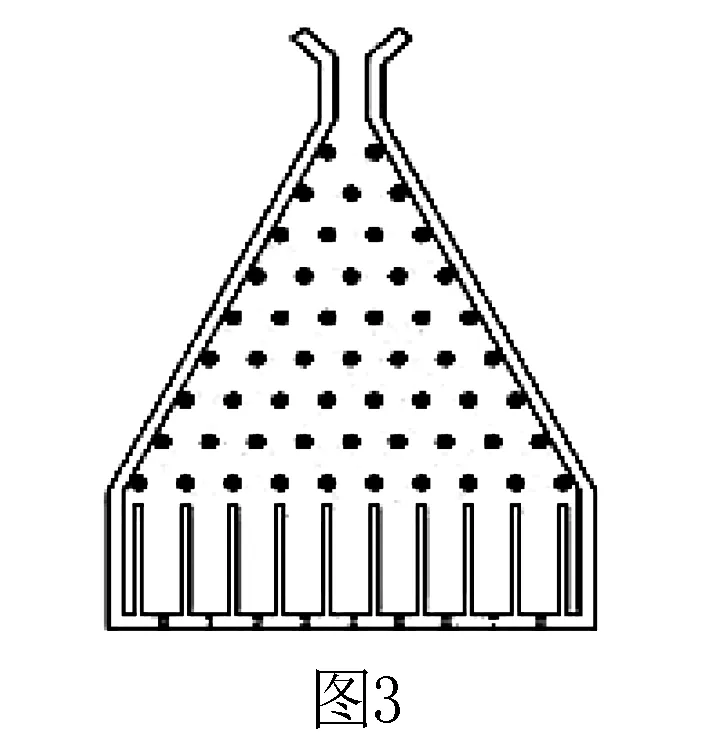
如圖3的高爾頓板,若小球碰到阻擋物后等可能地向兩側跌落,再次遇到障礙物后繼續等可能的向兩側跌落,以此類推,一直下跌,直到最終落入底層.
1.在圖3的高爾頓板中,求:
(1)小球落入第4層第3個通道的概率P(4,3);
(2)小球落入第n+1層第k(k≤n)個通道和第n+1層第k+1個通道的概率之和.
分析高爾頓板的原型為楊輝三角,利用楊輝三角的基本性質和數量關系即可解決問題.
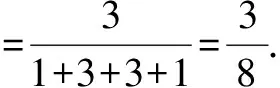
(2)根據楊輝三角的特點有
事實上,我們可以用數學歸納法證明如下定理:
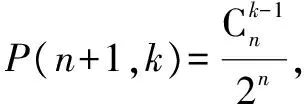
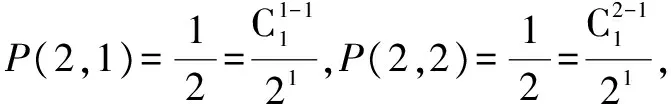
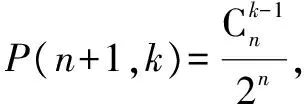
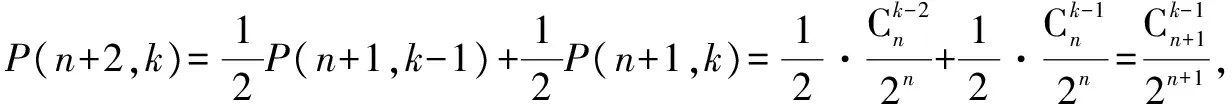
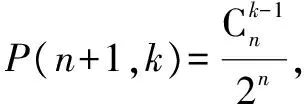
三、楊輝三角與縱橫路線圖
例4 縱橫路線圖是一類有趣的數學問題.圖4是某城市的部分街道圖,縱橫各有5條路,從A處走到B處且路徑最短,共有多少種不同的走法?
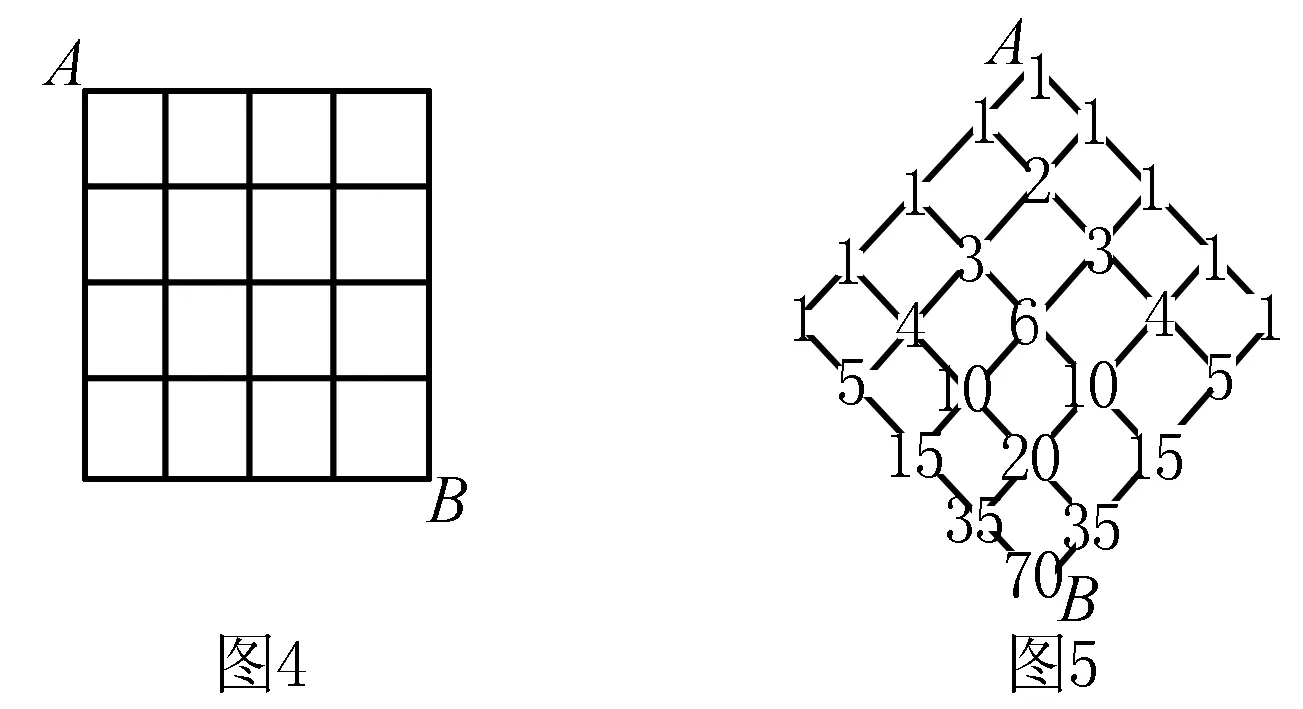
解我們把圖5順時針旋轉45度,然后在交叉點標上楊輝三角對應的數,如圖6.一般地,每個交點上的數就是從A處到達該點的方法數,故答案是70.
四、楊輝三角與萊布尼茨三……
登錄APP查看全文
猜你喜歡
中等數學
中等數學(2021年4期)2021-12-04 13:57:52
中等數學
中等數學(2021年7期)2021-12-03 04:01:41
中等數學
中等數學(2021年1期)2021-12-02 03:08:08
中等數學
中等數學(2021年3期)2021-12-02 00:28:14
中等數學
中等數學(2020年11期)2020-12-18 01:23:21
我們愛數學
學苑創造·A版(2019年5期)2019-06-17 01:14:21
我為什么怕數學
新民周刊(2016年15期)2016-04-19 18:12:04
數學到底有什么用?
新民周刊(2016年15期)2016-04-19 15:47:52
我難過,因為我看到數學就難過
傳奇故事(破繭成蝶)(2015年7期)2015-02-28 09:29:27
數學也瘋狂
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21
猜你喜歡
中等數學(2021年4期)2021-12-04 13:57:52
中等數學(2021年7期)2021-12-03 04:01:41
中等數學(2021年1期)2021-12-02 03:08:08
中等數學(2021年3期)2021-12-02 00:28:14
中等數學(2020年11期)2020-12-18 01:23:21
學苑創造·A版(2019年5期)2019-06-17 01:14:21
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
傳奇故事(破繭成蝶)(2015年7期)2015-02-28 09:29:27
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

