學會多角度尋找解題思路

李月恬 陳德前

(江蘇省姜堰區實驗初級中學 225500;江蘇省興化市教育局教研室 225700)

本文以一些典型的中考題為例，來談談如何多角度地尋找解題思路.

例1 若2a-b=5，則多項式6a-3b的值是____．

解法1 (參數代入法)將a當做已知數(參數)，根據“減數等于被減數減去差”，可得b=2a-5，則6a-3b=6a-3(2a-5)=6a-6a+15=15.

解法2 (整體代入法)把6a-3b變形為3(2a-b)，然后把2a-b整體代入，即可求得其值.6a-3b=3(2a-b))=3×5=15.

解法3 (特值代入法)取a=0，則b=-5，當a=0，b=-5時，6a-3b=0-3×(-5)=15.

反思回味：對于給定的條件，要善于從多角度來看，這里解法1 是將字母a看作常數來參與運算的；方法2是從整體的角度來看的，從待求的代數式中變換出已知條件式2a-b，整體代入，十分簡捷，也可以將已知式兩邊同時乘以3，整體得出結論；方法3是從特殊與一般的角度來看的，巧妙地取a=0，則b為整數-5，代入求值式計算比較簡捷，在用這種方法解題時要注意兩點：一是所取的字母值要使已知式和求值式有意義，二是所取的字母值要使計算簡便.

例2 化簡：x-{-5x-〔-y+(-x+3y)+x〕}.

分析本題中含有多層括號，可以先去小括號，再去中括號，最后去大括號； 也可以先去大括號，再去中括號，最后去小括號；聯想到學習相反數時化簡多重括號的方法，還可以得到一種更簡捷的方法：要確定每一項最后結果的符號，就是數“-”號的個數，如果是奇數個，那么結果的符號為負；如果是偶數個，那么結果的符號為正，這樣就可以一次性去掉所有括號．

解法1 原式=x-{-5x-〔-y-x+3y+x〕}=x-{-5x-〔+2y〕}=x-{-5x-2y}=x+5x+2y=6x+2y.

解法2 原式=x+5x+〔-y+(-x+3y)+x〕=6x-y+(-x+3y)+x=7x-y-x+3y=6x+2y.

解法3 原式=x+5x-y-x+3y+x=6x+2y．

反思回味：解法1是解決這類問題時最常用的方法，即從里到外去括號，要注意每去一次括號后就要將可合并的同類項合并起來，這樣就減少了項數，既可以避免錯誤，又可以簡化計算. 解法2與解法1的思路正好相反，從外向里去括號，運用了整體思想，去大括號時，將中括號看作一個整體，去中括號時將小括號看作一個整體.解法3給出了化簡多重括號的一種簡捷方法，即通過數“-”號的個數來判斷每一項最后結果的符號：如果是奇數個，那么結果的符號為負；如果是偶數個，那么結果的符號為正.這個法則可簡記為“奇負偶正” ．

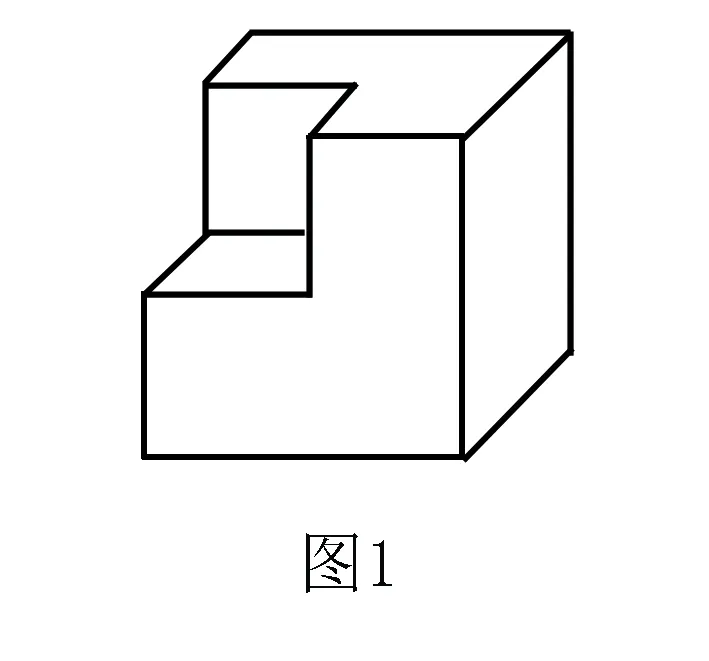
例3 從棱長為2的正方體毛坯的一角，挖去一個棱長為1的小正方體，得到一個如圖1所示的零件，則這個零件的表面積為 ．

分析解決本題首先想到的是計算出各個“外露”部分表面的面積，再求和，容易產生遺漏或重復；仔細觀察發現，從正方體毛坯中挖去一個棱長為1的小正方體，則這個零件的表面積通過補形就等于原正方體的表面積，計算就十分簡單.

解法1 這個零件的表面積=2×2×3+1×1×3+(2×2-1×1)×3=24.

解法2 這個零件的表面積=2×2×6=24.

反思回味：這類題的最大特點是不需要怎樣去計算，只靠仔細觀察結合實際經驗，就很容易解決，掌握視圖的概念是解題的關鍵.這里采用的技巧就是補形，即將問題中的原圖形(非規則圖形或非特殊圖形)經過添加輔助線以后，轉化為一個完整的特殊圖形，讓問題中的隱含條件顯露出來，從而使問題得以簡捷獲解．

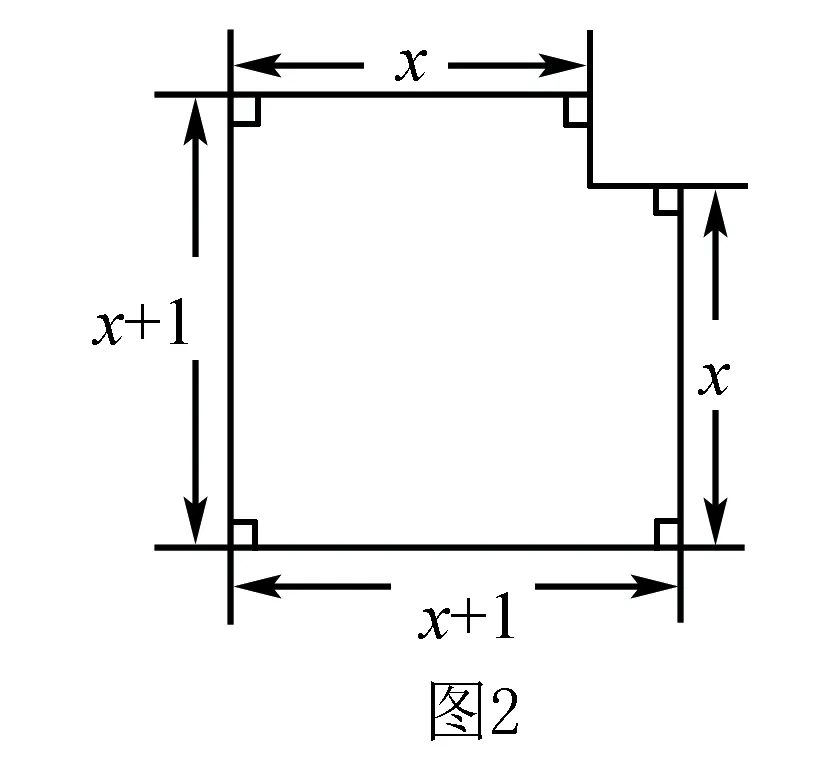
例4 已知如圖2所示的圖形的面積為24，根據圖中的條件，可列出方程： ．

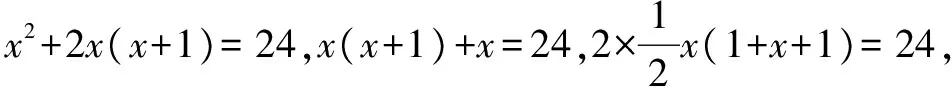
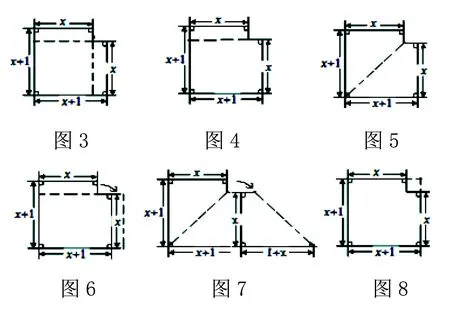
反思回味：本題盡管是一道“小題”，但它“小題大做”，能充分考查了不同層次解題者的思維水平和數學思想方法的應用能力．在每一種思路下得到的方程的簡繁程度是一目了然的，但這些方程本質上是相同的，因此給出的眾多答案可以把不同層次解題者的思維層次充分地映射出來，所以說，本題是題目小，功能大．

例5 災后重建，四川從悲壯走向豪邁．災民發揚偉大的抗震救災精神，桂花村派男女村民共15人到山外采購建房所需的水泥，已知男村民一人挑兩包，女村民兩人抬一包，共購回15包．請問這次采購派男女村民各多少人？( ).

A．男村民3人，女村民12人

B．男村民5人，女村民10人

C．男村民6人，女村民9人

D．男村民7人，女村民8人

分析這是一道典型的實際問題應用題，隨著我們思考角度的不同，解法也不一樣：

視角1(設直接未知數列一元一次方程求解的角度)：題目中有兩個等量關系：一是男村民人數+女村民人數=15人，二是男村民挑的水泥包數+女村民挑的水泥包數=15包．現在要求的是這次采購派男女村民各多少人，有兩個未知數，根據第一個等量關系知，可設直接未知數，設其中一個未知量為x人，則由第一個等量關系可知另一個未知量為(15-x)人，再由第二個等量關系列方程求解．

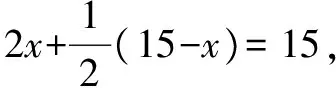
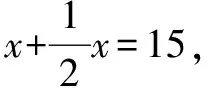
視角2(設間接未知數列一元一次方程求解的角度)：題目中有兩個等量關系：一是男村民人數+女村民人數=15人，二是男村民挑的水泥包數+女村民挑的水泥包數=15包．現在要求的是這次采購派男女村民各多少人，這可以通過求出男、女村民挑的水泥包數來求出．根據第二個等量關系，可設間接未知數，設其中一個未知量為x包，則由第二個等量關系可知另一個未知量為(15-x)包，再由第一個等量關系列方程求解．

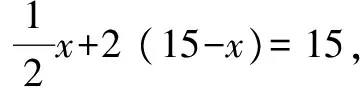
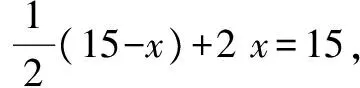
視角3 (從分組的角度)：因為男村民一人挑兩包，女村民兩人抬一包，所以可以把一個男村民和兩個女村民分成一組，每組3人挑3包水泥，15個人可以分為5組，5組15人挑15包水泥，這樣這次采購派男女村民人數就一目了然了．

解法3 一個男村民和兩個女村民分成一組，則每組3人挑3包水泥，則5組村民15人正好挑15包水泥，5組中有5個男村民和10個女村民，選B．

反思回味：解決實際問題應用題，方程是最有效的模型之一，隨著未知數選擇的不同，得到的解法也不一樣；數量關系選擇的不同，得到的解法也不一樣；由于題目沒有要求用方程來求解，所以采用算術方法來解決本題更簡捷.

[1]杭永根，陳德前.開放探究問題(3)[J].中學數學教學參考(中旬)，2017(1-2)：105-109.

[2]霍彩霞.如何進行審題[J].初中生學習指導(七年級)，2016(7-8)：98-101.