氫原子與類氫原子核外電子概率密度分布的比較研究
張 宇,唐啟祥
(文山學院 信息科學學院,云南 文山 663099)
氫原子核外電子的概率分布特點是量子力學教學中的重要內容之一,是初學者建立微觀粒子狀態按概率分布概念的必備知識,也是德布羅意波理論在氫原子體系中的直接體現。采用圖像表征很直觀,便于初學者對該理論的理解。現行的量子力學教材中,對氫原子核外電子的徑向概率分布函數Wnl(r)和角向概率分布函數Wlm(θ)進行了初步的描述,繪制了幾個示例性的二維平面圖,但對繪制的方法沒有作說明;對氫原子核外電子在三維空間的概率分布函數Wnlm(r,θ,φ)及三維分布圖沒有介紹和表征;氫原子與類氫原子核外電子的概率分布的對比研究也不見報道。
作為物理學專業的學生,通過對量子力學中氫原子理論的深入學習,在指導教師的指導下,沿著這樣的技術路線進行了研究:首先,通過查閱資料整理出氫原子及類氫原子體系核外電子徑向波函數和角向波函數[1-14];其次,將波函數轉換成相應的概率分布函數;第三,通過MATLAB軟件編程表征概率分布,實現其可視化;第四,比較兩種體系核外電子的概率分布特點,得出它們的異同之處。
1 核外電子概率分布
1.1 徑向波函數及徑向概率分布函數
在球坐標系中,氫原子和類氫原子具有相同形式的波函數:
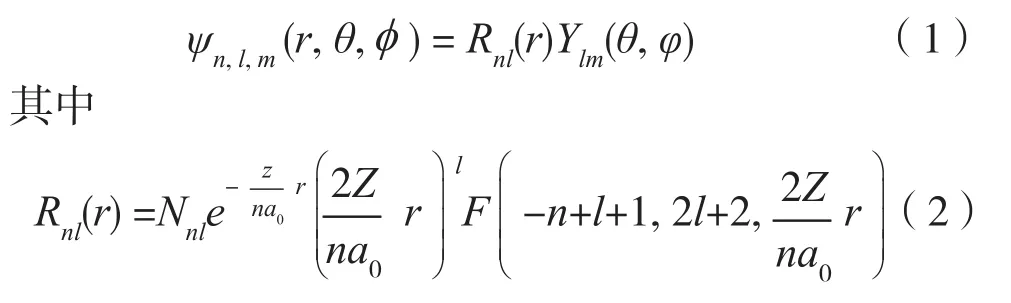
為徑向波函數,質子數Z=1對應于氫原子,Z≠1對應于類氫原子。Nnl為歸一化系數,a0為氫原子的第一波爾軌道半徑,為合流超幾何函數。Ylm(θ,φ)為角向波函數,是球諧函數,具體形式為:

式中,(cosθ)為連帶勒讓德多項式,Nlm為歸一化系數。
氫原子處于ψn,l,m(r,θ,φ)態時,電子在點 (r,θ,φ)周圍的體積元dr=r2sinθdrdθdφ內的概率為:

將式(4)對θ從0→π,對φ從0→2π積分,便可得到在半徑r到r+dr的球殼內找到電子的概率為:

Wnl(r)就是徑向概率密度分布函數。表1給出了幾個低量子數的徑向波函數和徑向概率密度分布函數。

表1 徑向波函數和徑向概率密度分布函數
1.2 角向波函數及角向概率分布函數
氫原子和類氫原子核外電子的角向分布函數都是式(3)中的相同的球諧函數[1]

為了方便描述,將角量子數l= 0, 1, 2, 3……的態分別稱為s,p,d,f態,處于這些態的電子,依次簡稱為s,p,d,f……電子。
對r從0→∞積分,可以得到電子在(θ,φ)方向附近立體角d?= sinθdθdφ內的概率為:

式(6)為角向概率密度分布函數。表2列出了幾個低階角向波函數和角向概率密度分布函數。

表2 角向波函數和角向概率密度分布函數
1.3 三維空間波函數及概率密度分布函數
氫原子及類氫原子體系在球坐標系的三維空間的波函數為:

式中n= 0, 1, 2, … ;l= 0, 1, 2, … ,n-1; m=0, ±1,±2,… ; ±l。
氫原子及類氫原子核外電子空間概率密度分布函數為:

表3給出了三維空間中體系的幾個波函數及概率分布函數。

表3 三維空間氫原子體系的波函數及概率密度分布函數

續表3
2 MATLAB對概率分布的模擬
2.1 氫原子核外徑向電子概率分布圖
通過MATLAB編程運行得到了n=1, 2, 3;l=0,1, 2的幾個氫原子徑向分布的圖。氫原子電子徑向位置概率密度分布的節點數目(不包括原點和無窮遠點)有nr=n-l-1個。特別地,基態氫原子和“圓軌道”(即l=n-1)的電子徑向位置概率分布沒有節點。比如,n=1,l=0,則nr=0,即氫原子徑向位置概率分布的節點數為0;n=2,l=0,則nr=1,即氫原子徑向位置概率分布的節點數為1;n=3,l=2,則nr=0,即氫原子徑向位置概率分布的節點數為1。如圖1所示。

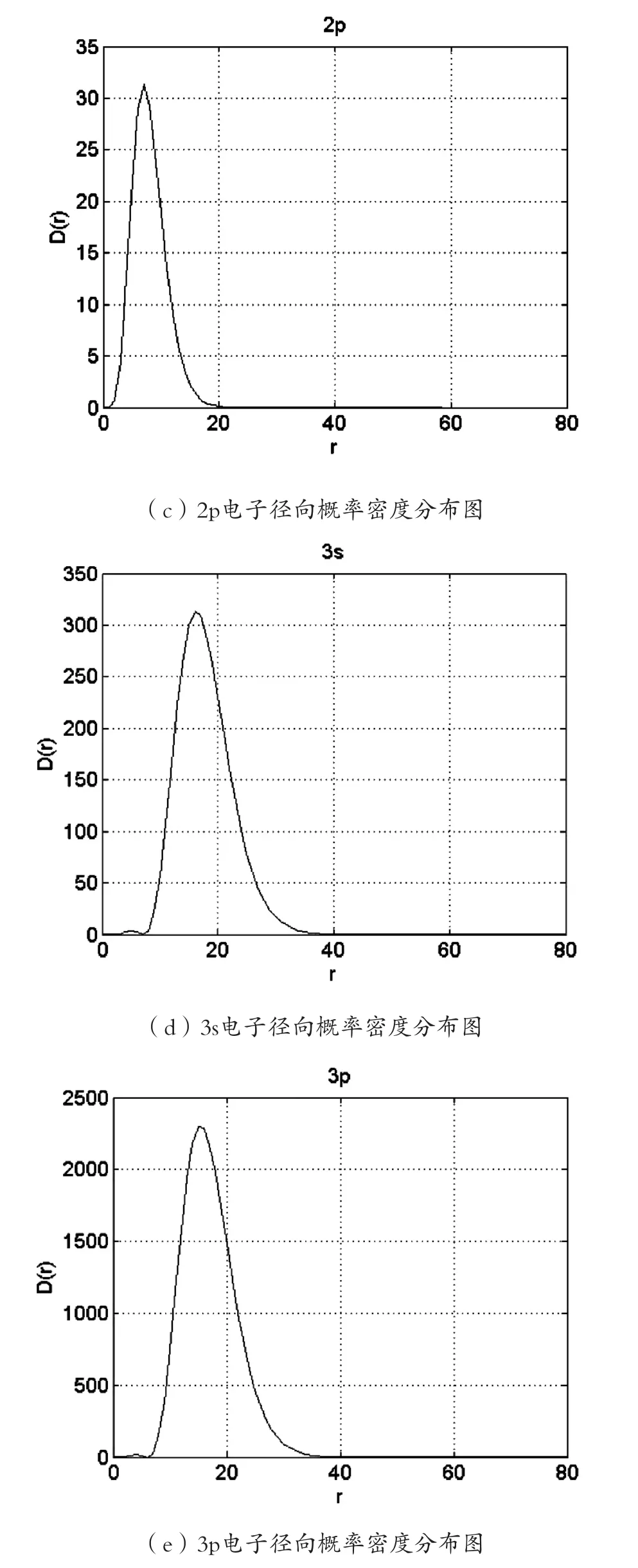

圖 1 不同狀態下氫原子徑向概率分布函數曲線
2.2 氫原子核外角向電子概率密度分布圖
通過MATLAB編程運行得到了l=0,1,2的幾個氫原子徑向概率分布的情況,見圖2:
1)l=0和m=0時,|Y00|2是一個均勻的球體,如圖2(a)所示;2)當l=1,m=0,±1時,|Y10|2由兩個均勻等值球體豎直重疊在一起構成,|Y11|2是兩個均勻的球體,在水平方向兩球對接構成,|Y1-1|2由兩個均勻等值球體水平對接在一起構成,如圖2(b)所示;3)當l=2,m=0和1時,|Y20|2是兩個均勻的球體加一個圓餅狀,在豎直方向兩球對接與圓餅上下構成;|Y21|2由4個兩兩均勻等值球體豎直方形對接在一起構成,形成花瓣狀,如圖2(c)所示;4)當l=2;m=-1和2,|Y2-1|2是4個均勻的球體兩兩相同,在豎直方向兩球對接與構成,形成花瓣狀。|Y22|2由4個兩兩均勻等值球體水平方向對接在一起構成,形成花瓣狀,如圖2(d)所示。
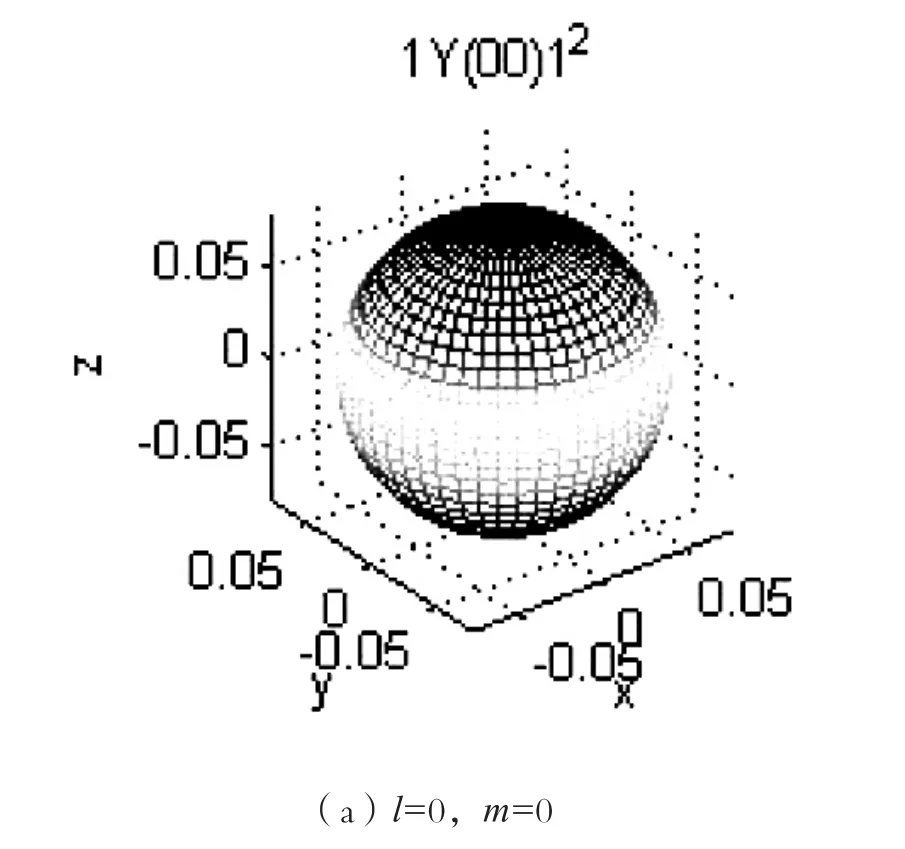
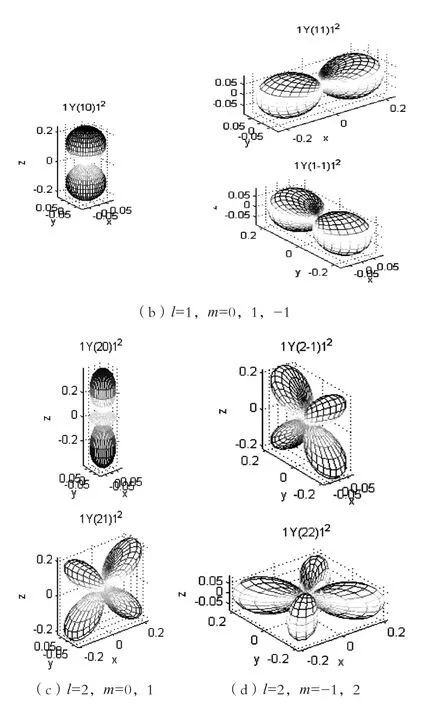
圖 2 不同狀態下氫原子及類氫原子核外電子角向概率密度分布圖
2.3 三維空間電子概率密度分布
利用MATLAB軟件編程繪制了氫原子各狀態下空間電子概率分布切片圖,切片圖上顏色灰度的深淺表示電子幾率密度的大小,其中顏色深表示電子幾率密度大。從空間幾率分布電子云圖可以更加直觀地看出氫原子電子云的分布情況。作出n=1, 2, 3;l=0, 1, 2;m=0, ±1,±2的核外電子概率分布圖的空間電子云圖。分析比較,具有如下的特點:
1)當n=1,l=0和m=0時,|W100|2是一個均勻的單鋒體,等高線圖分布均勻及顏色對比圖明顯,如圖3(a)所示;2)當n=2,l=1,m=0時,|W210|2由一個均勻等值單峰體構成,等高線圖分布均勻及顏色對比圖有明顯的分布情況,如圖3(b)所示;3)當n=2,l=1;m=±1時,|W211|2是兩個均勻的單峰體構成,在水平方橫向兩峰對接構成,等高線圖線條疏密明顯,如圖3(c)所示;|W21-1|2由兩個均勻等值單峰體水平對接在一起構成;在水平方縱向兩峰對接構成,線條疏密分布明顯,如圖3(d)所示。


圖 3 不同狀態下氫原子電子空間分布及空間概率分布等高線圖
3 氫原子與類氫原子核外電子徑向概率密度分布圖的對比
3.1 徑向概率密度對比圖及其分析
由于類氫原子與氫原子核外電子的角向分布函數完全一樣,不受質子數Z的影響,它們的概率密度函數完全相同,分布圖也完全一樣,此處不再呈現。在相同的n,l情況下,氫原子和不同Z值的類氫原子的徑向概率密度分布圖顯示,隨著質子數Z值的增大,圖形會越來越小,表示電子更靠近原子核,如圖4所示。
3.2 概率密度極大值與質子數之間的變化關系圖
以rmax表示第1次出現徑向概率密度極大值,繪制rmax隨質子數Z變化的函數圖像。從1s,2s,和3s各個原子態的情況可見,類氫原子徑向概率密度極大值rmax隨Z值增大而減小,表示核外電子分布隨質子數的增加而向原子核靠攏,符合庫侖定律的基本要求,結果如圖5所示。

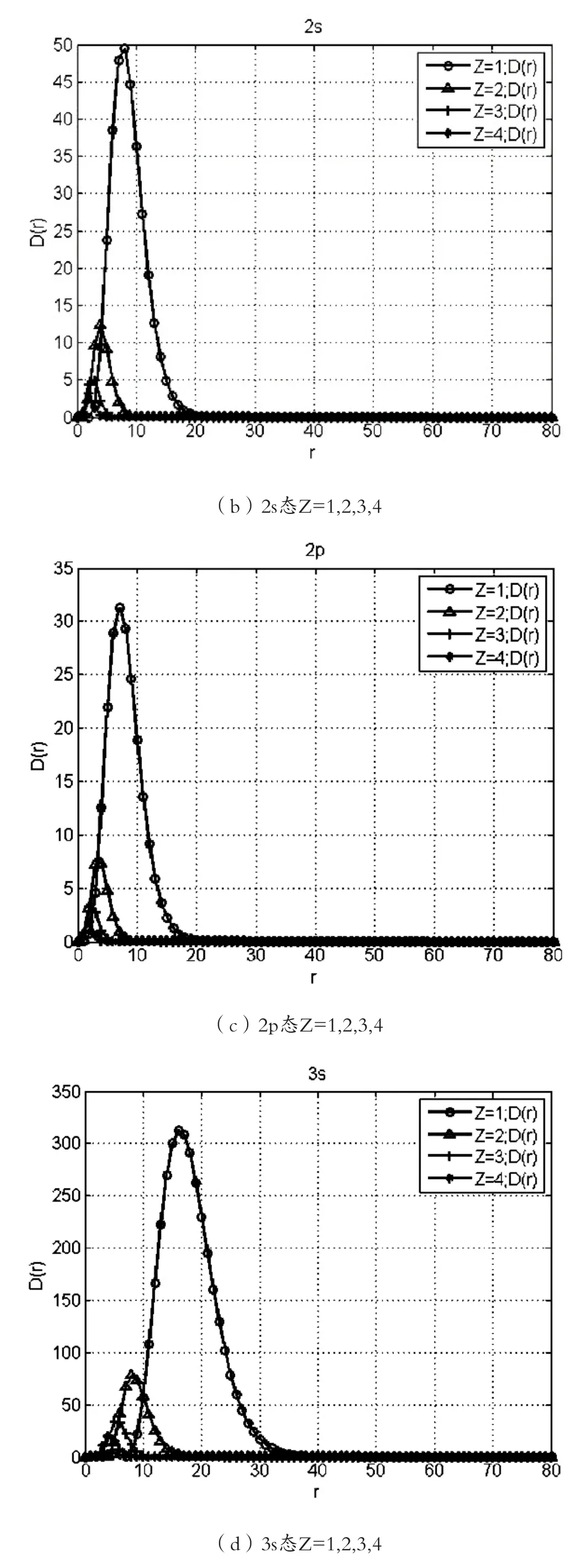

圖 4 Z=1,2,3,4的氫原子及類氫原子徑向概率密度分布對比圖


圖 5 不同Z值的氫原子及類氫原子rmax-Z圖
4 結論
通過整理及MATLAB軟件繪圖對比分析可知:
1)無論是氫原子體系還是類氫原子體系,相同量子態的角向概率密度分布函數都是一樣的;不同量子態電子概率密度的分布不一樣,但總體上表現出非常嚴格的對稱性。
2)相同量子數對應的量子態徑向概率密度分布相似,但隨原子核內質子數Z的增大,概率密度的極大值位置向原子核靠攏,符合庫侖定律的基本要求。
[1] 周世勛.量子力學教程[M].北京:高等教育出版社,1979:36.
[2] 楊林. 氫原子電子概率分布可視化及其I 生質研究[J].綏化學院學報,2009(2):186-188.
[3] 馬德明,仇海強,施衛.氫原子電子云分布的可視化分析[J].西安理工大學學報,2007(2):149-152.
[4] 趙云芳,周戰榮,李育新.氫原子電子云的計算和可視化分析[J].大學物理,2009(9):51-54.
[5] 郭仕恒,許慶陵,王東耀,蘇育志,張建華.基于MATLAB的球諧函數M函數庫[J].廣州大學化學化工學院學報,2011(10):1-2.
[6] 宮建平.氫原子的概率密度分布[J].晉中學院學報,2015(3):10-15.
[7] 陸云清,劉洋,鄧玲玲.氫原子電子云空間分布的可視化[J].南京郵電大學學報,2009(5):8-23.
[8] 張建華,蘇育志,宋建華,郭海燕.用 origln6.0 繪制波函數平面圖形[J].計算機與應用化學,2003(4):467-470.
[9] 李金海,方恒忠,李子良.氫原子電子云密度分布分析[J].大學物理,2004(3):13-17.
[10]劉建軍,高峰,華厚玉.氫原子波函數三維空間分布在MATLAB 中的實現[J].淮北煤炭師范學院學報,2004(4):31-33.
[11]鄧明森.基于計算機仿真技術的氫原子電子云圖模型[J].貴州教育學院學報:自然科學,2005(2):35-37.
[12]趙旭光,劉曉軍.用MATLAB獲得氫原子的電子云圖像[J].齊齊哈爾大學學報,2006(5):98-100.
[13]王向賢,蔡志剛,許明坤.類氫原子徑向波函數數字化教學軟件[J].巢湖學院學報,2010(6):124-127.
[14]郭振華.類氫原子中電子橢圓軌道量子化的一個簡化推導[J].寶雞文理學院學報,1997(12):46-53.

