顯見與隱匿共存 拾錯與引錯并舉

李培芳

【摘要】化錯教學(xué)法在小學(xué)數(shù)學(xué)一線教師中有諸多積極的響應(yīng)者與實踐者。要將化錯教學(xué)法付諸教學(xué)實踐應(yīng)當探明兩個問題：一是學(xué)生學(xué)習(xí)“差錯”可能的存在形式；二是面對學(xué)生的學(xué)習(xí)“差錯”，教師教學(xué)適切的化錯方式。本文擬就上述兩方面問題進行一些探討。

【關(guān)鍵詞】化錯教學(xué)法 拾錯 引錯

著名特級教師華應(yīng)龍老師從30多年的教學(xué)實踐與探索中提出了“化錯”的教育思想，在其教育思想指導(dǎo)下形成了具有鮮明特色的化錯教學(xué)法。化錯教學(xué)法的提出，對眾多“只見數(shù)學(xué)不見學(xué)生”的數(shù)學(xué)課堂無疑是開出了一劑良方。

化錯教學(xué)法在一線教師中有諸多響應(yīng)者與實踐者，該教學(xué)法在教學(xué)實踐中備受推崇的原因是多方面的。一方面該教學(xué)法在教學(xué)實踐中“立竿見影”，取得了極好的教學(xué)效果；另一方面化錯教學(xué)法背后有堅實的理論支撐。葉瀾教授認為：沒有轉(zhuǎn)化就沒有真正的學(xué)習(xí)。可見轉(zhuǎn)化之于“教師的教”與“學(xué)生的學(xué)”都至為關(guān)鍵。那么，問題或許便在于“轉(zhuǎn)化什么”了。恩格斯指出：最好的學(xué)習(xí)是從錯誤中學(xué)習(xí)。美國實用主義教育家杜威認為：思維起源于某種疑惑、迷亂或懷疑。這種疑惑與迷亂往往表現(xiàn)為學(xué)生認知中的錯誤（當然有些疑惑不一定會以可見的錯誤呈現(xiàn)）。而化錯教學(xué)法正是對學(xué)生認知的錯誤進行巧妙轉(zhuǎn)化的教學(xué)方法。可見，即便從理論上進行邏輯的推演，也可以想見化錯教學(xué)法是一種有效、有意義且值得推廣的教學(xué)方法。

要將化錯教學(xué)法付諸教學(xué)實踐應(yīng)當探明兩個問題：一是學(xué)生學(xué)習(xí)“差錯”可能的存在形式有哪些；二是面對學(xué)生的學(xué)習(xí)“差錯”，教師教學(xué)時恰切的應(yīng)對方式有哪些。本文擬就上述兩個問題結(jié)合具體的教學(xué)案例進行一些探索。

【案例】

課前，老師先畫好一段弧AB（如下圖）在黑板上，同時擦去圓心。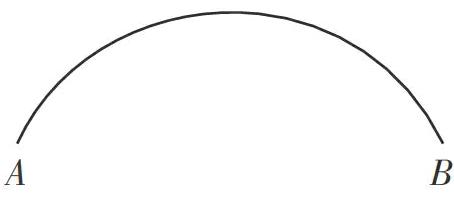

上課，教學(xué)“弧AB”（略）

師：同學(xué)們，今天咱們學(xué)習(xí)扇形。

（板書課題：扇形）

師：要研究扇形，得有一個扇形吧，這樣，黑板上已經(jīng)有一條弧了，誰能在這基礎(chǔ)上畫出扇形來。

生1利用直尺畫出下圖。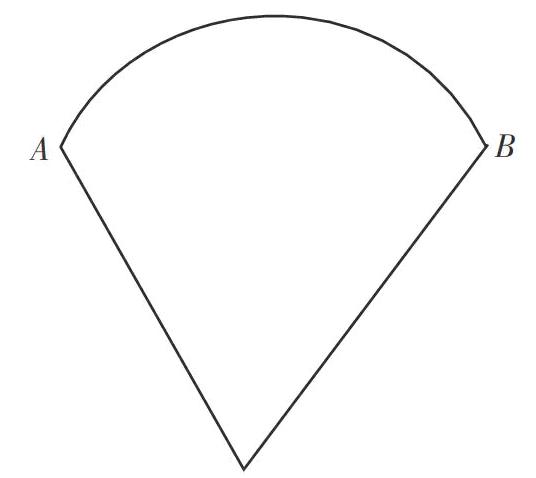

生2：這不是扇形，因為歪了。

生3：不是扇形，歪向左邊了。

生4：扇形是對稱的，這個圖形不對稱。

師：看來，大家心里都有一個扇形啊！扇形是對稱的，那該怎么畫才能畫出扇形呢？

生5：先畫出對稱軸，再畫就可以畫出扇形了。

（生5上臺操作，老師協(xié)助其完成下圖）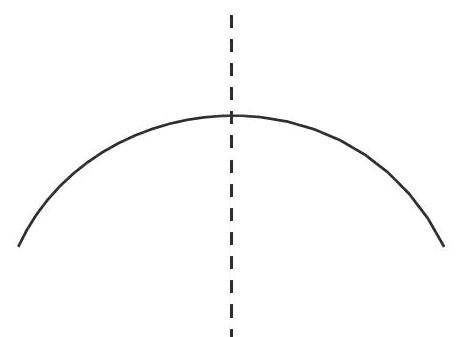

師：有了這條對稱軸幫忙，誰能畫出一個扇形？

請生1上臺畫。（圓心在O處）

請生5上臺畫。（圓心在P處）形成下圖：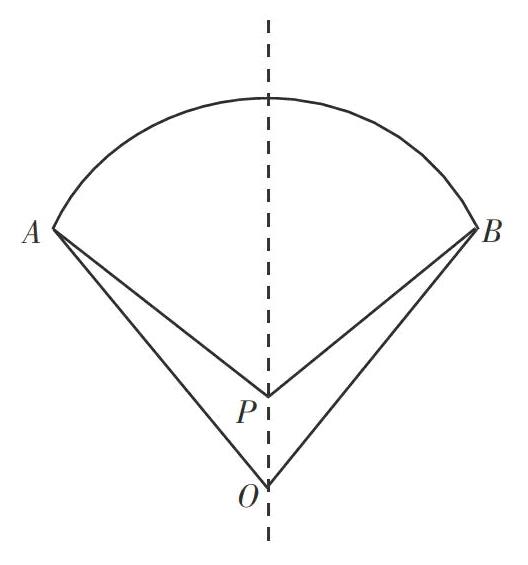

師：同學(xué)們，這里有兩個圖形，你認為哪一個是扇形？或者都是扇形？

大部分學(xué)生認為都是扇形。

師：這樣，這兩個圖形到底是不是扇形，同學(xué)們到書中去找答案好嗎？

學(xué)生自學(xué)課本第75頁。

生1：這兩個都是扇形，因為它們都是弧AB和經(jīng)過這條弧兩端的兩條半徑所圍成的圖形，所以它們都是扇形。

大部分同學(xué)認同。

生2：扇形是圓形的一部分，這兩個圖形不一定是扇形。

生1質(zhì)疑：這兩個圖形正是圓形的一部分啊！

生2無語坐下。

生2激動地：老師我能不能到上面畫？

（畫出下圖）

生2：難道這個也是扇形嗎？這個也是圓的一部分嗎？

生1：是啊！只是這個圓更大了，是一個更大的圓的一部分。

生2無語坐下。

師：表決一下，認為這里的三個圖形都是扇形的舉手。

全班除了生2沒舉手，其他同學(xué)全部舉手。

師對生2說：這樣，你是不是覺得這不是一個圓的一部分，這樣，你把這個圓畫出來看看，不就知道是不是圓的一部分了。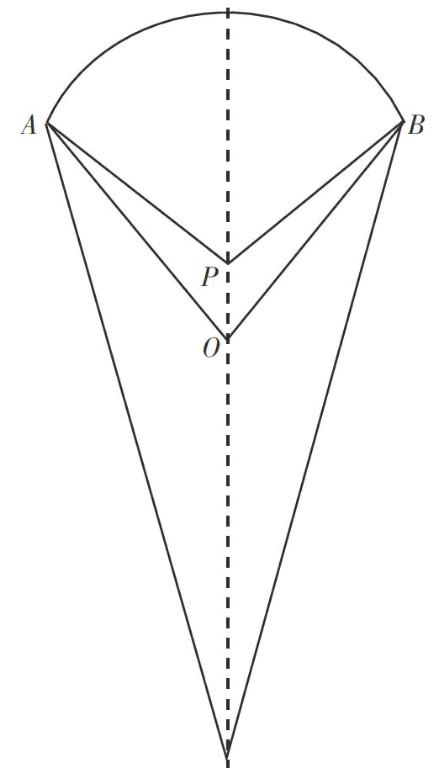

生2上臺操作，如下圖：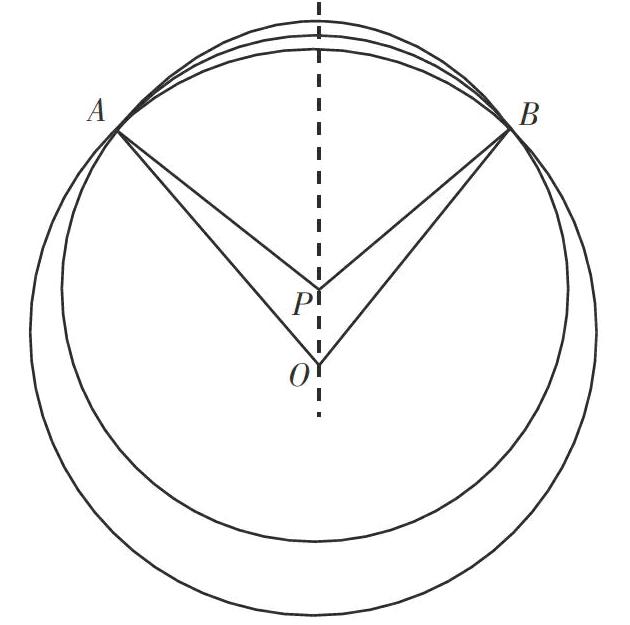

生2激動地：這兩個不是扇形，弧不在那里，弧沒有重合。

生2補充：因為點P和點O都不是弧AB的圓心。

師：你剛才也是這個意思嗎？

生2：我剛才不是這個意思，但是好像是這個感覺。

師對生1說：你想說點什么嗎？

生1：這兩個都太像扇形了，不過扇形的頂點要在圓心，要有一個圓心角。

全體同學(xué)若有所思

……

【思考】

一、學(xué)生學(xué)習(xí)的差錯“顯見”與“隱匿”共存

“錯誤可能有無窮的結(jié)合方式”（盧梭），學(xué)生對于一個問題的認知差錯都可能是“各錯其錯”。很難想象，學(xué)生對于所有問題的認知差錯會豐富與復(fù)雜成什么樣？因此，要將學(xué)生的差錯進行分類幾乎不可能！不過，從差錯隱蔽的程度來說不外乎顯見與隱匿兩種。

顯見的差錯與隱匿的差錯對于學(xué)生的認知都是至為重要的養(yǎng)分。對于學(xué)生顯見的差錯，老師們的思考與分析較多，因其可見，因其常見。而對于隱匿的差錯，相關(guān)研究不多，本案例的價值在于提供了一個“藏得極深”的差錯，引發(fā)我們認真去思考那些隱藏在自然而然的“想當然”之下的謬誤。

本案例產(chǎn)生于筆者的突發(fā)奇想，當這個靈感閃現(xiàn)時，筆者拿著下圖問了學(xué)校很多語文老師，他們都說這兩個是扇形。之后，筆者轉(zhuǎn)而問學(xué)校的數(shù)學(xué)老師，大部分老師也說這兩個都是扇形。這個發(fā)現(xiàn)讓人興奮不已，看來，大家對扇形的認識有問題，這個問題在于弧與半徑的對應(yīng)關(guān)系，一般人還真看不出來！這個差錯藏得很深，將這個差錯呈現(xiàn)出來，一方面有利于學(xué)生對扇形概念的正確理解，另一方面可以領(lǐng)略數(shù)學(xué)的嚴謹與精確之美。

二、教師的化錯應(yīng)當“拾錯”與“引錯”并舉

當學(xué)生的差錯極為隱蔽時，這個差錯其實是更有價值的，然而這樣的差錯同時也是最不容易暴露出來的。

華應(yīng)龍老師所倡導(dǎo)的化錯教學(xué)，在捕捉學(xué)生差錯方面，提出了兩個策略：一個是“拾錯”，另一個是“創(chuàng)造機會，暴露差錯”（筆者稱之為“引錯”）。前一策略提出的“拾”有主動尋找的意思，這種主動尋找既是意識上的，也是行為上的。后一個策略闡述的是：當一種差錯在自然的狀態(tài)下不可能出現(xiàn)時，教師有必要“創(chuàng)造”機會，將差錯“引”出來。這樣一來，顯見的差錯使用“拾錯”的策略，隱匿的差錯使用“引錯”的策略。這兩條策略形成一個封閉的網(wǎng)，網(wǎng)住教師想呈現(xiàn)的每一個學(xué)生的差錯。

那么，如何讓隱匿的差錯可見呢？

首先是“看到差錯”，教師本身要意識到這個差錯的存在，而能形成這樣的意識取決于對教學(xué)內(nèi)容本質(zhì)的理解與把握及對學(xué)生認知水平與可能的判斷。

其次是“進入差錯”，通過創(chuàng)造易錯的問題，讓學(xué)生進入疑惑與迷亂之中，讓他們的認知“錯誤地走一回”，這個過程不是故弄玄虛，而是學(xué)生認知的必由之路，這種感覺是美妙的，那是一種走出迷宮的感覺。這種經(jīng)過掙扎、經(jīng)過糾結(jié)而形成的認知才是深刻的，我們將這種深刻與美妙的東西稱之為“體驗”。

而后是“辯明對錯”，組織討論或爭辯。讓學(xué)生在討論中思考，在爭辯中明晰。

最后，“愛上這個錯”，引導(dǎo)學(xué)生辯證地看待差錯本身，辯證地看待差錯對于學(xué)習(xí)的價值。最后達到華應(yīng)龍老師所倡導(dǎo)的“融錯”的境界。

三、化錯教學(xué)的核心在于展現(xiàn)真實的差錯本身

從上面的案例中，我們還可以得到這樣的啟示：有的錯，可能無法完美化錯，但是無論如何，應(yīng)當讓學(xué)生暴露真實存在的差錯。教師即使沒能找出好的化錯方式（如本課例），差錯的呈現(xiàn)仍然是必不可少的教學(xué)過程。或者是不是可以這樣說：化錯教學(xué)的核心在于展現(xiàn)真實的差錯本身。

“繞開錯誤就是繞開認知過程的豐富性”（華應(yīng)龍語），但凡學(xué)生認知中的差錯都應(yīng)該暴露出來，不管是顯見的還是隱匿的，這是毋庸置疑的。試想，將差錯藏起來是多么可笑的想法，這種荒唐不亞于掩耳盜鈴。

【參考文獻】

[1]華應(yīng)龍、華應(yīng)龍與化錯教學(xué)[M].北京：北京師范大學(xué)出版社，2015.

[2]約翰·杜威.我們怎樣思維.經(jīng)驗與教育[M].北京：人民教育出版社，2005.