基于地表能量平衡和ARMA的南極洲地表溫度研究

高夢，李勇，宣琳，宋運澤

(1.安徽財經大學 管理科學與工程學院；2.安徽財經大學 統計與應用數學學院；3.安徽財經大學 會計學院，安徽 蚌埠 233030)

?

基于地表能量平衡和ARMA的南極洲地表溫度研究

高夢1，李勇2，宣琳2，宋運澤3

(1.安徽財經大學 管理科學與工程學院；2.安徽財經大學 統計與應用數學學院；3.安徽財經大學 會計學院，安徽 蚌埠 233030)

針對南極洲平均地表溫度問題，借助MATLAB、EVIEWS、VC++等軟件，綜合運用了地表能量平衡、線性擬合、時間序列分析等方法，建立了地表能量平衡、多元線性回歸、自回歸移動平均等模型，定義與估計南極洲平均地表溫度并對其隨時間推移的變化情況進行了研究，得出南極洲在2015年6月正午的平均地表溫度為-37.4543℃、當年平均地表溫度受到滯后一期溫度的影響等結論.

南極洲；平均地表溫度；地表能量平衡；ARMA；VC++；MATLAB

0 引 言

地球表面的平均溫度是影響氣候變化和全球變暖的一個關鍵因素.然而，人們在怎樣定義和估算平均地表溫度上有一些方法上的差異，并且以往估算平均地表溫度的方法多為根據少數氣象站的數據進行插值平均，其結果存在較大誤差.為了更加準確地估計平均地表溫度，本文以南極洲為例，利用氣象站數據，建立數學模型來定義和估計南極洲的平均地表溫度，并對其隨時間推移的變化情況進行了研究.

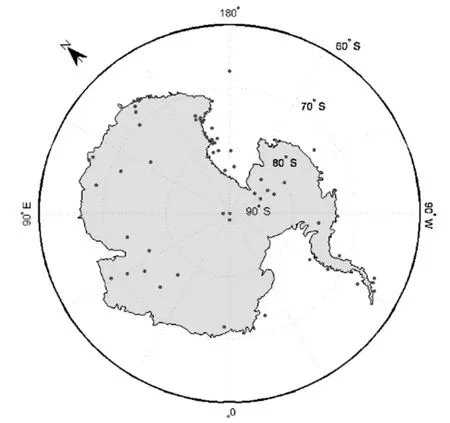
圖1 研究區及氣象站點分布圖

1 地表溫度的求解

1.1 研究思路

為了定義和估算南極洲平均地表溫度，首先要由南極洲的近地表溫度計算出南極洲的地表溫度.通過大英南極洲調查網站[1]得出南極洲67個氣象站處的近地表溫度，建立地表溫度平衡模型，得出南極洲67個氣象站處的地表溫度.

南極洲區域內的67個自動氣象站分布情況如圖1所示，可以看出，氣象站整體分布較為均勻，數據可以很好地反應南極洲的真實氣候水平.

1.2 研究方法

根據地表能量平衡模型[2]，利用氣象站的近地表溫度估算地表溫度.公式為

Ts=-Ta-1.82+10.66cosα(1-NDVI)-0.56A+ 3.72(1-β)[cosγ/cosα+(π-B)/π]R+3.14Δh

(1)

其中，Ta為近地表溫度(℃),TS為地表溫度(℃)，α是太陽天頂角，NDVI是歸一化植被指數，A是太陽方位角，β是地表反照率，γ是入射角，B是坡度，R是到達地表的太陽短波輻射(kW/m2)，Δh是氣象站的高程和其周圍20 km平均高程的差值(km).

選取2015年6月22日正午12點各氣象站的近地表溫度來計算這一時刻各氣象站的地表溫度，通過大英南極洲調查網站獲取相關數據，其中，以2015年6月正午12點的平均溫度作為6月22日正午12點的溫度.同時，通過大英南極洲調查網站得到各氣象站所在位置的緯度值.

根據公式(1)，利用地表能量平衡法計算地表溫度，其中，南極的地表反射率β=0.79[3]；歸一化植被指數是反映農作物長勢和營養信息的重要參數之一，-1≤NDVI≤1，負值表示地面覆蓋為云、水、雪等，對可見光高反射[4].由于南極洲常年大面積覆蓋冰面，植被極少，所以其歸一化植被指數為負值，結合南極洲的地理情況，取NDVI=-0.8.

根據公式(1)，利用地表能量平衡法計算得出各氣象站地表溫度情況(見表1).其中，ID表示南極洲67個氣象站的ID，近地表和地表分別表示近地表溫度和地表溫度(單位：℃).

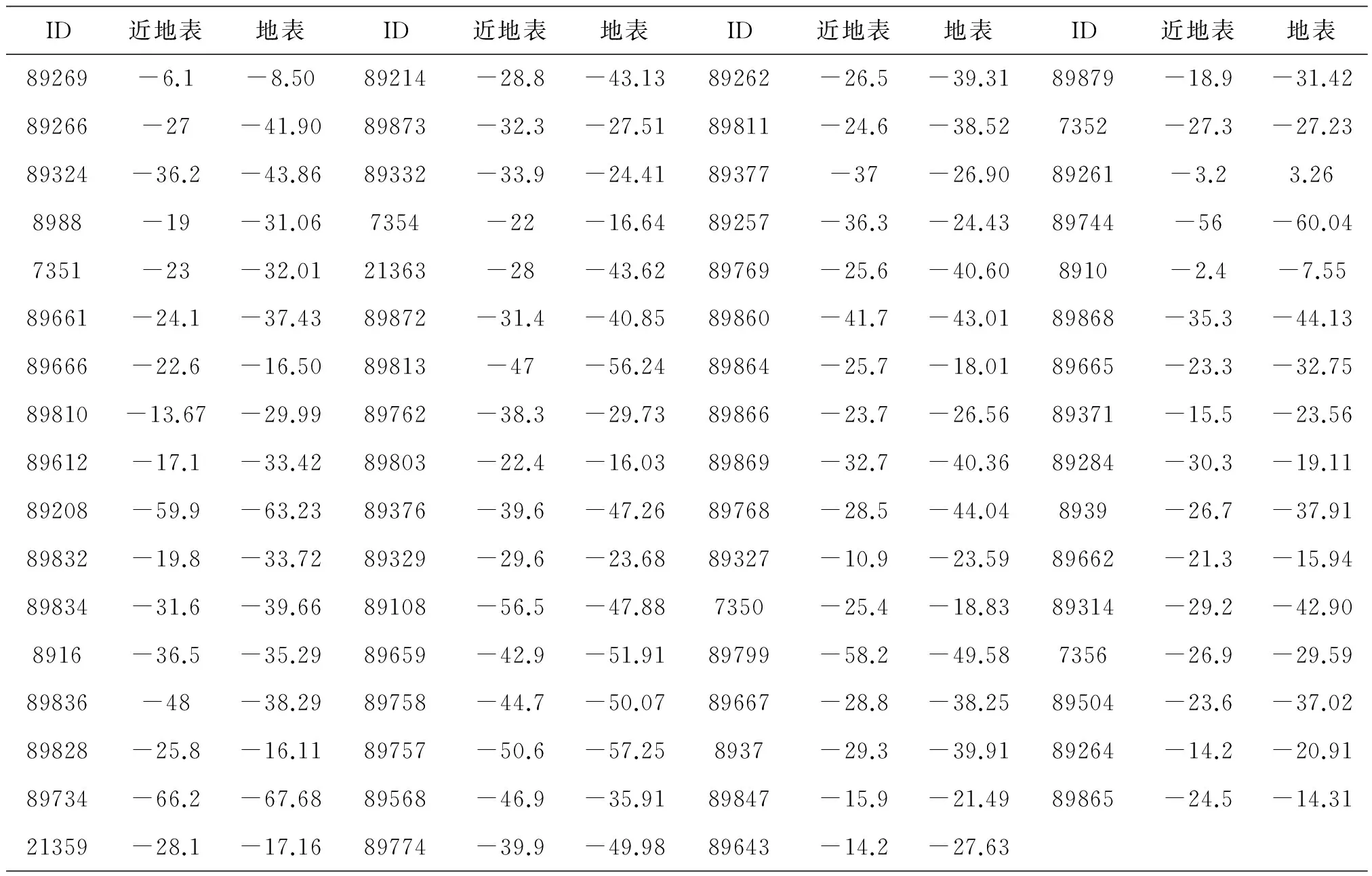
表1 各氣象站近地表和地表溫度值

1.3 結果分析

由表1作出67個自動氣象站的近地表溫度和地表溫度的對比情況(如圖2所示).

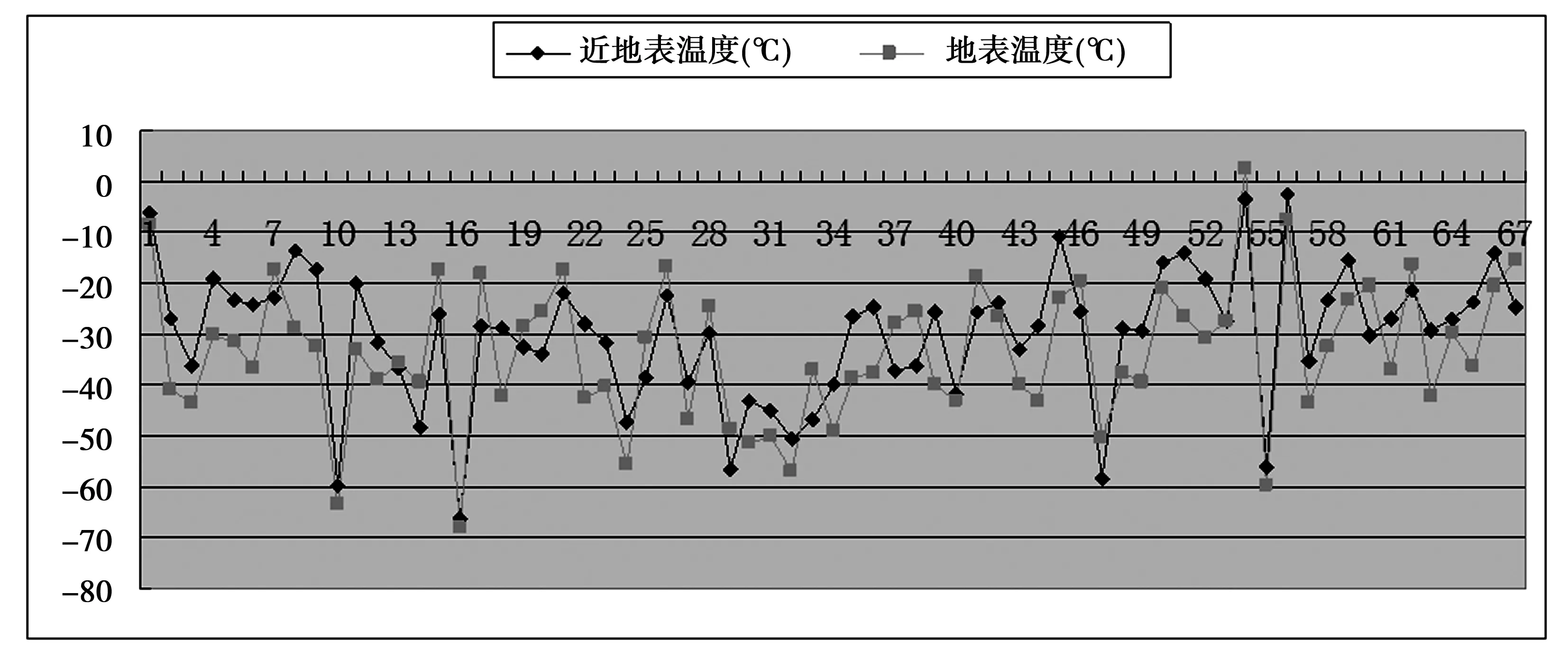
圖2 近地表溫度與地表溫度對比情況圖

由圖2可以看出，地表溫度的變化比近地表溫度的變化要劇烈，且多數自動氣象站的地表溫度低于近地表溫度，這與南極洲常年冰雪覆蓋的地理狀況是相符合的.

2 平均地表溫度的定義與估算

2.1 研究思路

以往計算平均地表溫度的方法多為根據少量氣象站的地表溫度進行插值平均，對于南極洲而言，其總面積為1424.5萬km2，面積廣闊.而南極洲內僅有67個自動氣象站，若通過插值和簡單平均得出平均地表溫度，誤差是很大的.因此本文對平均地表溫度的定義是：以不同海拔高度所在的圓周周長為權重，以該海拔高度的平均地表溫度為因子，進行加權平均，所得結果即為南極洲平均地表溫度.通過多元線性回歸得出近地表溫度關于緯度、高度、經度等因素的回歸方程，通過線性擬合得出地表溫度關于近地表溫度的一元線性方程，從而通過取不同的緯度、經度、高度得出多個非氣象站的地表溫度，然后依據本文的定義加權平均得出南極洲的平均地表溫度.

2.2 研究方法

2.2.1 多元線性回歸模型[5]

以2015年6月22日正午12點這一時刻為例，計算平均地表溫度，通過大英南極洲調查網站獲得67個自動氣象站的緯度、經度、高度和近地表溫度.

以自動氣象站的緯度、經度、高度三個指標為自變量，以近地表溫度為因變量，建立多元回歸模型.分別作出三個指標與近地表溫度的散點圖(如圖3到圖5所示).

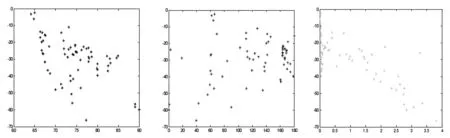
圖3 緯度與近地表溫度 圖4 經度與近地表溫度 圖5 高度與近地表溫度

從圖3-圖5中可以看出，經度與近地表溫度之間沒有明顯關系；緯度和高度均與近地表溫度呈線性負相關關系，即隨著緯度或高度的增加，近地表溫度均降低.

設緯度、經度、高度分別為x1,x2,x3，近地表溫度為y，建立多元回歸模型y=b0+b1x1+b2x2+b3x3+ε.利用MATLAB軟件編程，剔除異常點后得到在可決系數為0.9158時，近地表溫度與緯度、經度、高度的函數關系為

(2)

2.2.2 非線性擬合模型

根據表1中的數據，對近地表溫度和地表溫度進行一元線性擬合，首先求出它們的相關性系數為0.7760，具有比較好的正相關性，可以進行擬合.以近地表溫度為自變量x，地表溫度為因變量y，利用MATLAB軟件編程，得到的擬合曲線如圖6所示，得出的一元線性擬合方程為y=0.82586*x-8.8924.

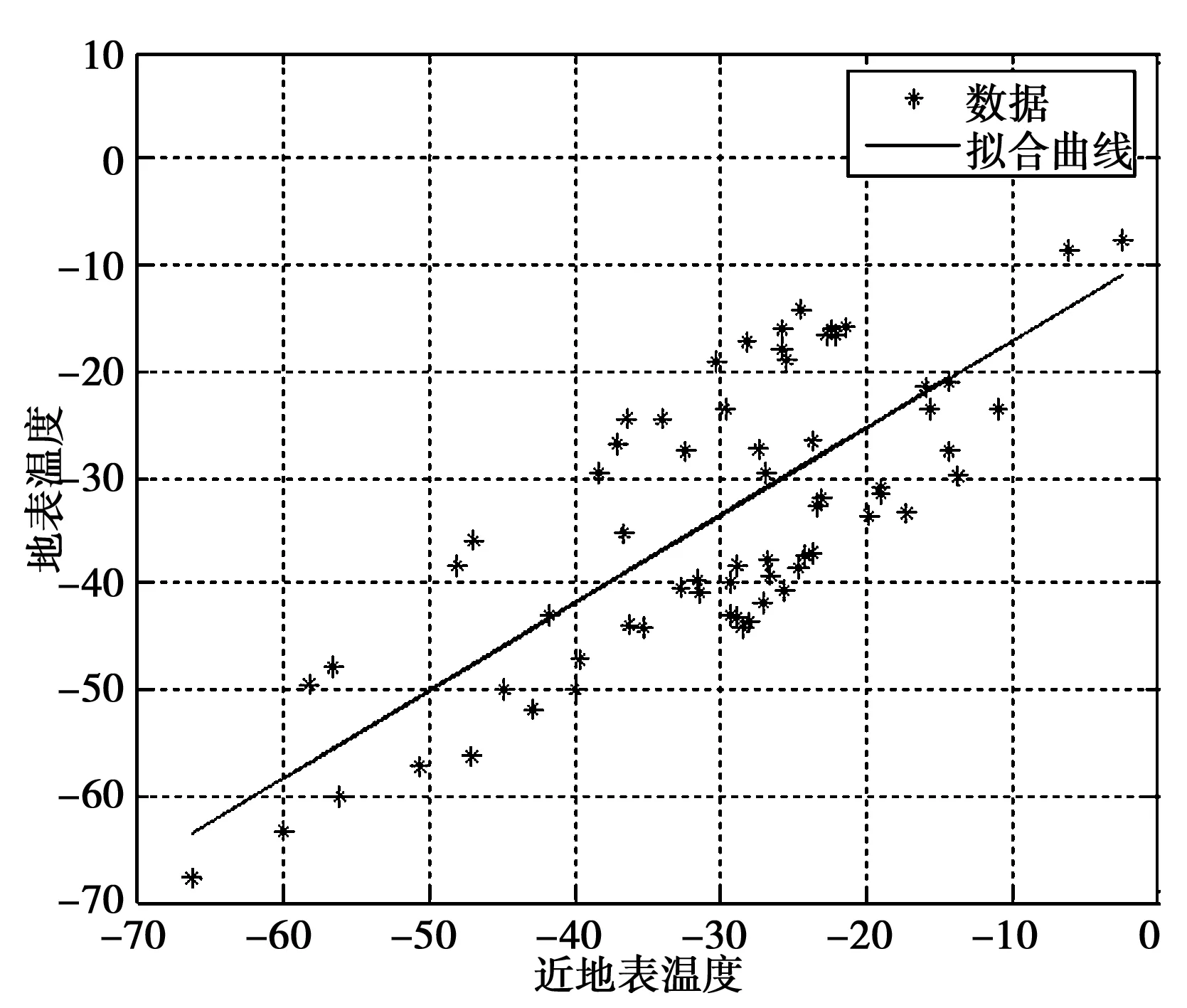
圖6 一元線性擬合圖

2.2.3 平均地表溫度求解模型

根據多元線性回歸方程和一元線性擬合方程計算多個位置的地表溫度.南極洲的緯度范圍為南緯60 (°)到南緯90 (°)，經度范圍幾乎為0到360 (°)，最高海拔高度為5140 m.因為南極洲在海拔1 km以內的地表面積較大，海拔1 km以上的地表面積較小，所以在海拔1 km以內，取高度間距為100 m，緯度間距為5 (°)，經度間距為90 (°)；在海拔1 km以上，取高度間距為500 m，緯度間距為5 (°)，經度間距為90 (°).利用VC++6.0軟件編程[6]，得到不同高度、緯度、經度共665個位置的地表溫度.

所取的海拔高度為1 km以內間距為100 m，1 km以上間距為500 m，共19個海拔高度.對于計算出的665個位置的地表溫度，求出每一海拔高度的平均地表溫度，每一海拔高度的權重和平均地表溫度(見表2).

表2 各海拔高度平均地表溫度(℃)和權重表

根據表2，加權平均得出南極洲的平均地表溫度為-37.4543 ℃.

2.3 結果分析

南極洲的年平均溫度為-25 ℃，全洲最冷月(7月)沿海平均氣溫在-20—-30 ℃,內地在-40—-70 ℃，本文模型中為6月份的南極洲平均地表溫度，因為平均地表溫度與平均空氣溫度比較接近，所以求出的南極洲平均地表溫度是合理的.

3 南極洲地表溫度的變化研究

3.1 研究思路

為描繪隨時間的推移南極洲溫度的變化情況，首先做出1986年至2015年地表溫度序列的時間路徑圖，判斷該序列為非平穩時間序列.再借助EVIEWS做出該序列的自相關與偏相關圖，發現自相關函數值與偏相關函數值都在1階后衰減于0，識別出該序列符合ARMA(1,1)模型，并對模型進行估計，通過估計方程描繪出南極洲溫度的變化.

3.2 研究方法

由于近地表溫度與地表平均溫度趨勢基本一致，且用近地表溫度計算得到地表平均溫度的擬合效果較好，所以利用67個自動氣象站的平均近地表溫度作為南極洲地表溫度的近似替代.考慮到數據是1959年至2015年監測值，數據量較大，為了直觀地反映這57年南極洲地表溫度的變化，利用EVIEWS做出近地表溫度的時間路徑圖(如圖7所示). 由圖7可以看出隨著時間的變化，地表溫度呈現規律的波動，且序列的均值不為0[7]，故該時間序列可能是非平穩的時間序列.若一個時間序列是非平穩的，一般經過去趨勢或者差分處理后可以得到平穩的時間序列.從經驗上來說，大部分時間序列都是差分平穩時間序列而不是趨勢平穩時間序列.因此，我們對這個時間序列進行差分處理(如圖8所示).

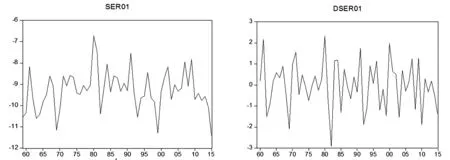
圖7 地表溫度序列的時間路徑圖 圖8 一階差分序列的時間路徑圖

由圖8可得數據沒有明顯的趨勢，在零附近上下波動，且均值為零，說明原序列的一階差分序列是平穩時間序.借助EVIEWS對新生成的序列作出自相關圖與偏自相關圖[8](如圖9所示).

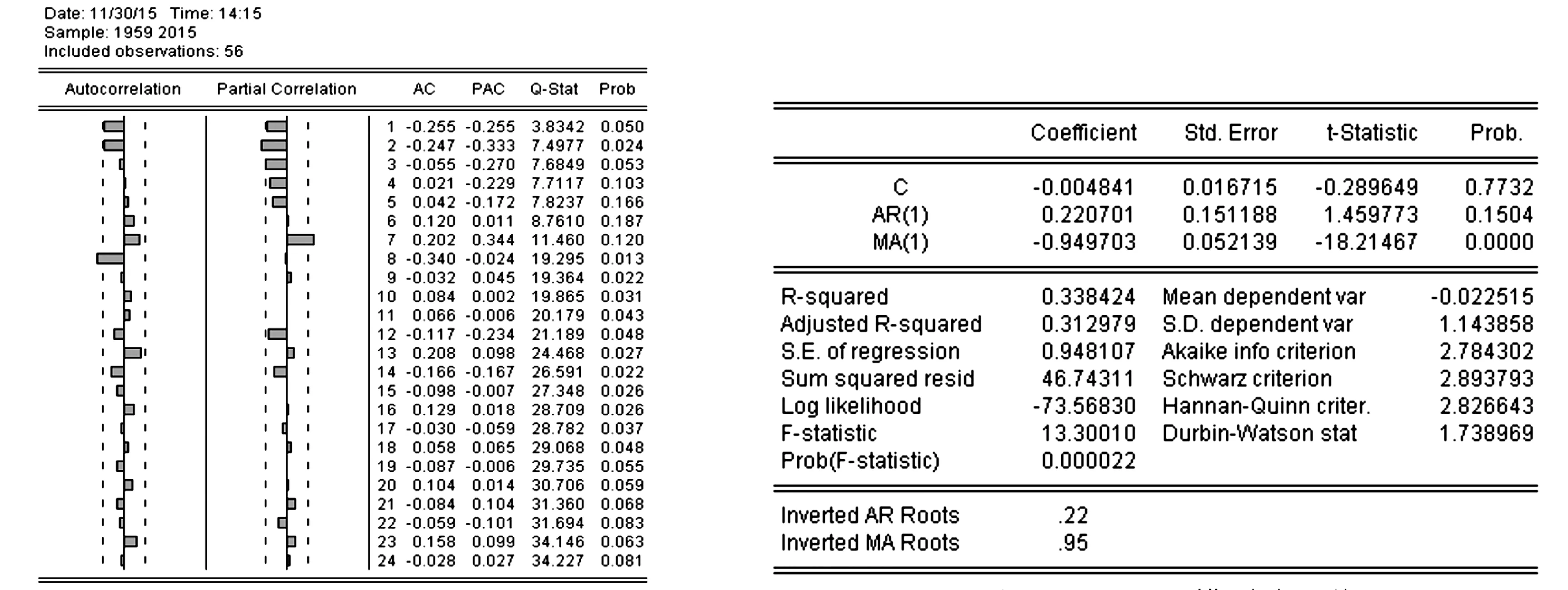
圖9 時間序列一階差分后的ACF和PCAF圖 圖10 ARMA模型估計值

由圖9可得自相關函數值與偏相關函數值都在一階后衰減于零，因此利用ARMA模型進行求解.ARMA模型是一種比較成熟的模型，要求時間序列是隨機與平穩的，且模型的關鍵是階數的確定與參數的估計.

3.3 結果分析

利用EVIEWS，進行ARMA模型相關操作，就得到了模型的估計結果(如圖10所示).

根據運行結果，得出估計方程為：dy=-0.0048+0.22dyt-1-0.948et-1+et.說明當年地表平均溫度對下一年的地表平均溫度有0.22的貢獻率，且當年平均地表溫度受到殘差與殘差滯后一期的影響.

4 小 結

以上各模型在建模過程中通過多種相應的軟件檢驗，具有一定的合理性.本文針對已有定義和估算平均地表溫度方法的不足，以南極洲為例給出了新的定義和估算方法，得出了南極洲某一時刻的平均地表溫度，并研究了南極洲地表溫度隨時間推移的變化情況.這一方法還可以用于估算南極洲其它時刻的平均地表溫度、其它地區某一時刻的平均地表溫度以及其它地區溫度隨時間的變化情況，具有一定的推廣性.

[1]大英南極洲調查網站.https://legacy.bas.ac.uk/met/READER/[EB/OL].

[2]徐偉燕,孫睿,金志鳳，等.基于MODIS 數據的近地表氣溫估算[J].氣象與環境科學,2015,38(1):1-6.

[3]劉樹華,熊康.南極瑞穗站輻射特征的初步研究[J].北京大學學報,1993,29(1):96-106.

[4]張遠東,張笑鶴,劉世榮.西南地區不同植被類型歸一化植被指數與氣候因子的相關分析[J].應用生態學報,2011,22(2):323-330.

[5]李艷嬌,李瑞敏,陳經偉.多元線性回歸的MATLAB實現[J].常熟理工學院學報,2014,28(2):49-52.

[6]譚浩強.C程序設計教程(第2版)[M].北京:清華大學出版社，2013:104-108.

[7]王麗娜,肖冬榮.基于ARMA模型的經濟非平穩時間序列的預測分析[J].武漢理工大學學報,2004,28(1):133-136.

[8]閆博,周在金,李國和，等.基于ARMA和BP-AdaBoost的組合銷售預測模型研究[J].計算機與現代化,2015(2):14-18.

[責任編輯：王軍]

Research on the surface temperature of antarctica based on surface energy balance and ARMA

GAO Meng1,LI Yong2,XUAN Lin2,SONG Yunze3

(1.School of Management Science and Engineering, Anhui University of Finance & Economics;2.School of Statistics and Applied Mathematics, Anhui University of Finance & Economics;3.School of Accountancy, Anhui University of Finance & Economics , Bengbu 233030, China)

Aims to work out the average surface temperature of Antarctica.Based on MATLAB, EVIEWS and VC++, the surface energy balance, linear fitting, time series analysis and other methods were used to establish the models of Surface energy balance, Multiple linear regression, Autoregressive moving average and so on.We define and estimate the average surface temperature of Antarctica, meanwhile we do some research on the changes of average surface temperature with time goes on.The conclusions are the average surface temperature of Antarctica at noon in June 2015 is -37.4543℃, and the average surface temperature is affected by next term and so on.

antarctica: average surface temperature; surface energy balance; ARMA；VC++; MATLAB

2016-04-29

國家級大學生創新項目(201510378086)

高夢(1995—)，女，安徽宿州人，安徽財經大學在讀本科生，主要從事信息管理與信息系統的研究.

李勇(1963—)，男，安徽蚌埠人，安徽財經大學數學教學研究中心主任，副教授，主要從事信息與計算科學的研究.

P423.7

A

1672-3600(2017)03-0007-05