關于二元初等函數在其定義域上連續性問題的分析

河南省鄭州工業應用技術學院基礎教學部 袁曉華

關于二元初等函數在其定義域上連續性問題的分析

河南省鄭州工業應用技術學院基礎教學部 袁曉華

函數連續性是高等數學中重要的概念，但二元初等函數在定義域上的連續性的判斷一直是學習的難點。基于這種認識，本文首先對定義域和定義區域進行了區分，然后對二元函數的連續性定義和二元初等函數在定義域上的連續性問題展開了分析，從而為關注這一話題的人們提供參考。

二元初等函數；定義域；連續問題

在多數數學教材中，既沒有明確進行定義域和定義區域的區別論述，同時也未對二元初等函數的連續性進行具體敘述。在這種情況下，學生學習多元函數連續性問題時常常感到困惑，從而無法較好地完成相關問題的理解。因此，相關人員還應該對二元初等函數在其定義域上連續性問題展開進一步分析。

一、二元初等函數的定義域和定義區域的區分

二元初等函數連續性的討論都圍繞著定義區域和定義域進行。比如在分析基本初等函數時，就會指出其在定義域內是連續的。但是在敘述多元初等函數時，則需要指明其是在定義區域內保持連續。所以在分析二元初等函數連續性之前，還應該了解定義區域和定義域的區別，以便幫助學生更好地認識多元初等函數。所謂的定義區域，就是在定義域內的區域或閉區域。比如在將使算式有意義的點集當成是函數的自然定義域時，其定義區域就是包含定義域的連通閉集或開集。因此，定義區域范圍更大，與定義域有明顯區別。

二、二元初等函數在其定義域上的連續性問題

1.二元函數的連續性定義

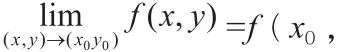
2.定義域上二元初等函數的連續性分析

由二元初等函數的定義可知，二元初等函數是利用一個式子表示的二元函數，所以其肯定為二元函數，也遵循二元函數的連續性定義。分析二元函數在定義域的連續性定義可以發現，其中并未對函數在一點相對于點集的連續性進行定義，并且也未對函數在孤立點上的連續性進行定義。而D的內點就是D的聚點，D的界點既有可能為D的聚點，也有可能為D的孤立點，在定義域D內，無論（x0，y0）為內點還是界點，想要了解函數在該點是否連續，還要確保（x0，y0）為D的聚點。所以，如果定義域內存在孤立點，就是函數的不連續點。因此，二元初等函數在定義域內連續的結論將被定義域中含有孤立點所打破。

3.二元初等函數在定義域上連續性定義

通過分析二元初等函數在定義域上的連續性可以發現，二元初等函數即便在點集上有定義，但是卻不一定在該點集上保持連續，所以，利用二元函數的連續性定義判定二元初等函數在定義域上保持連續，無法準確進行二元初等函數的連續性問題的敘述。由上面的例子可知，可以認為二元初等函數在除去孤立點的定義域上將保持連續，所以，根據這些內容，還應該對二元函數的連續性定義進行補充，從而更好地判斷二元初等函數在定義域上的連續性。具體來講，就是設點集D上函數f（x，y）有定義，并且在點集D上存在有點A（x0，y0）為D的界點，在ε＞0，且ξ＞0的條件下，如果A（x，y）∈∪（A0，ξ）∩D時，|f（x，y）-f（x0，y0）|＜ε，則可以認為函數f（x，y）在點A0處保持連續，也可以敘述為函數f（x，y）在點A0相對D上保持連續。在這一定義中，點A0為定義域D的孤立點，在∪（A0，ξ），由于ε＞0，且ξ＞0，所以除A0外的D中其他點不在∪（A0，ξ）內。而由于|f（A）-f（A0）|=|f（x，y）-f（x0，y0）|=0＜ε，因此可以證明孤立點Ao處的函數f（x，y）保持連續。在平時的分析中，通常稱在某點連續的函數為完全連續，所以，如果函數在該點完全連續，其在該點相對于包含點的任何點集也將保持連續。實際上，對所有的多元初等函數來講，函數在定義區域上是連續的，都不能說明其在定義域上也是連續的。對二元初等函數在定義域的連續性問題展開分析，能夠幫助學生更好的理解多元初等函數的這一特性。

總之，通過分析定義域與定義區域的區別，并且分析二元函數的連續性定義，可以發現二元函數在定義域上保持連續的結論并不成立，但其在定義區域上具有一定的連續性。因此，相信本文對二元初等函數在其定義域上的連續性問題展開的分析，可以為相關研究的開展提供指導。

[1]劉暢，史書陽.在判別二元函數連續性時學生常犯的錯誤[J].中國科教創新導刊，2008（23）：133.

[2]曹媛.函數連續性的幾個問題[J].天津職業院校學報，2010（02）：78-80.

[3]齊淵.多元函數連續性的判定方法[J].隴東學院學報，2009（05）：13-15.

袁曉華（1985）女，漢族，河南項城人，學位：碩士，職位：教師，職稱：助教，研究方向：非線性動力學】