談管道沿程阻力系數的計算
■劉文婷 胡寶林
〔北京中棉工程技術有限公司,北京100052〕
談管道沿程阻力系數的計算
■劉文婷 胡寶林
〔北京中棉工程技術有限公司,北京100052〕
軋花廠通風除塵與氣力輸送管道的阻力計算是合理選擇風機的主要依據,而阻力系數的計算是計算管道沿程阻力的關鍵。沿程阻力系數的大小與流體的流態有關,流體的流態可分為層流狀態和紊流狀態(也稱湍流),紊流又可以細分為過渡狀態、紊流狀態和完全紊流狀態。阻力系數與流態密切相關,流態不同阻力系數的計算方法也不同,界定流態的主要依據是雷諾數。
一、雷諾實驗
雷諾通過實驗發現液體在流動中存在兩種內部結構完全不同的流態:層流和紊流。同時也發現,層流的沿程水頭損失Hf與流速一次方成正比,紊流的Hf與流速的1.75~2.0次方成正比;在層流與紊流之間存在過渡區,Hf與流速的變化規律不明確。當流體流速較小時,流體質點只沿流動方向作一維的運動,與其周圍的流體間無宏觀的混合即分層流動這種流動形態稱為層流或滯流。流體流速增大到某個值后,流體質點除流動方向上的流動外,還向其它方向作隨機的運動,即存在流體質點的不規則脈動,這種流體形態稱為湍流。這個臨界值就是雷諾數,是無量綱數即無因次量,符號為Re。它反映了沿程阻力系數λ是與流態密切相關的參數,計算λ值必須首先確定流態。
雷諾數小,意味著流體流動時各質點間的黏性力占主要地位,流體各質點平行于管路內壁有規則地流動,呈層流流動狀態。雷諾數大,意味著慣性力占主要地位,流體呈紊流(也稱湍流)流動狀態,一般管道雷諾數Re<2 320為層流狀態,2 320≤Re<4 000為過渡狀態,Re>4 000為紊流狀態,Re>10 000為完全紊流狀態。
二、雷諾數的計算
雷諾數計算公式
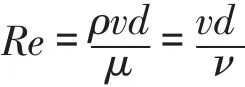

對于圓形管道來說,特征尺寸即為圓管直徑;非圓形管道則用當量直徑來代替。當量直徑等于水力半徑的4倍,水力半徑等于有效斷面面積與濕周長之比(濕周長就是流體固體邊界的接觸長度)。
三、阻力區域的劃分與判別
尼古拉茲對不同直徑的管道進行了一系列的實驗,采用人工方式模擬了管壁粗糙度,并按對數規律繪制了實驗曲線。該曲線分為5個阻力區域,每個阻力區域的雷諾數范圍如下。
(一)層流區
當Re<2 320時,沿程阻力系數只與Re有關,其關聯曲線在對數坐標圖上為一條直線。
(二)過渡區
當2 320≤Re<4 000時,出現了從層流向紊流過渡的不穩定現象,沿程阻力系數只與Re有關。
(三)光滑管區
(四)粗糙管區
(五)阻力平方區
科爾布魯克于公元1939年通過實驗研究總結了粗糙管區沿程阻力系數計算公式;在紊流粗糙管區內用此公式計算的沿程阻力系數精度較高,但求解λ過程較繁瑣,為了簡化計算過程,1944年莫迪在科爾布魯克公式的基礎上,通過對數坐標系繪制了工業管道λ的線算圖,即莫迪圖,可按Re及相對粗糙度直接查得λ值。莫迪圖即是科爾布魯克公式的圖解。(該圖可作為速查或粗略計算,但由于方格解析度和印刷線條細度有限,因此,一般只能讀取兩位有效數字。)隨著計算機技術的發展,計算已不是問題,因此主要通過公式計算阻力系數。
例如:軋花廠外吸棉管道直徑360 mm,輸送風速24 m∕s,絕對粗糙度0.2 mm,則Re=571 429,顯然處于粗糙管區,應用適合于粗糙管區的公式計算沿程阻力系數。
四、沿程阻力系數的計算公式簡介
(一)層流區
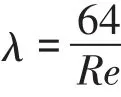
(二)過渡區
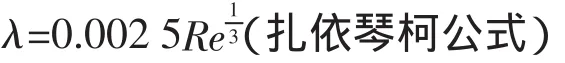
(三)光滑管區
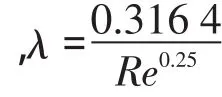

針對上例軋花廠外吸棉管道,當其絕對粗糙度為0.2 mm時,應用科爾布魯克公式計算結果:λ= 0.017 890 76和應用莫迪圖圖解結果:λ=0.018 0均能夠計算出沿程阻力系數。
五、結論

“十二五”國家科技支撐計劃項目課題(2015BAD19B04)
項目名稱:棉花產后增值關鍵技術裝備研發與產業化示范

