中橢圓軌道衛星多普勒頻移快速估計及分析*

喬文龍，章堅武，包建榮,2，姜 斌

（1.杭州電子科技大學 通信工程學院，浙江 杭州 310018；2.東南大學 信息科學與工程學院，江蘇 南京 210096）

中橢圓軌道衛星多普勒頻移快速估計及分析*

喬文龍1，章堅武1，包建榮1,2，姜 斌1

（1.杭州電子科技大學 通信工程學院，浙江 杭州 310018；2.東南大學 信息科學與工程學院，江蘇 南京 210096）

衛星通信中，星地雙方高速移動及快速角度變化等因素，將造成較大多普勒頻移及頻譜擴展等現象，惡化星地通信性能。在W alker星座計算多普勒頻移算法的基礎上，提出了改進的中橢圓軌道衛星多普勒頻移的快速簡化計算方法。相對于傳統衛星在宇宙空間的三維坐標復雜公式計算方法，所提方法通過長半軸、偏心率等參數直接計算衛星半徑，較大降低了計算復雜度。最后，仿真對比和分析高橢圓軌道通信衛星的多普勒頻移曲線，較好地解釋了中橢圓軌道多普勒頻移特性。同時，仿真星地在相對運動情況下的多普勒頻移特性，驗證了其有效性，以便于實際衛星通信場合快速估計多普勒頻移而有效輔助信號接收。

衛星通信；中橢圓軌道；鏈路通信；多普勒頻移

0 引 言

橢圓軌道因其在遠地點運動速度慢﹑角速度慢﹑覆蓋區域大﹑相對地面滯留時間長的軌道特性，成為對持續觀測某一地區的研究熱點，尤其是高緯度和兩極地區[1]。例如，運行在大橢圓軌道上由8顆衛星組網而成傾角為63.4°的前蘇聯戰略通信衛星“閃電”，可保證對本土全天候覆蓋[2]。在緯度較高的歐洲地區，歐洲航天局提出利用高橢圓軌道衛星系統對歐洲緯度大于56°地區實現高仰角覆蓋。由于高橢圓軌道衛星軌道遠地點高度約40 000 km，據地面觀測站的通信距離過長，導致鏈路通信損耗很大[3]。后設計出一種具有遠地點特性明顯﹑低鏈路傳輸損耗﹑組網衛星少等特點的中橢圓軌道衛星星座。該星座可以全天候多重覆蓋北緯0°～80°地區[4]，應用于未來高緯度地區的軍事通信﹑電子對抗﹑防空預警﹑軍事及民用導航定位等方面，前景廣闊[5]。對于兩極地區，可以使用單顆的高橢圓軌道通信衛星進行觀測覆蓋，這對于觀測極地環境海洋大氣變化，具有重要的價值[6]。和圓軌衛星的多普勒頻移相比，橢圓軌道的多普勒頻移變化也具有周期性，但更加復雜[7]。在赤道觀測點上觀測圓軌道衛星的多普勒頻移時間曲線已在文獻[8]中分析。文獻[9]推導了近地軌道（LEO）衛星的多普勒頻移表達式。文獻[10]給出了編隊小衛星在橢圓軌道下的幾何特性。文獻[11]提出了在圓軌道下中軌道和低軌道的多普勒頻移估計和補償算法。文獻[12]給出一種通過計算衛星三維坐標的多普勒頻移計算方法，但其存在計算量大的問題。針對這個問題，本文提出了一種簡化的中橢圓軌道衛星的多普勒頻移參數的估計公式，可以有效降低計算復雜度。同時，本文仿真多普勒頻移時間曲線，與高橢圓軌道衛星的多普勒頻移時間曲線對比，分析其多普勒頻移特性，對以中橢圓軌道建立星座進行通信領域具有極大的應用價值。

1 中橢圓軌道多普勒估計算法

多普勒頻移的基本表達式為：

其中，fc為載波頻率，c為光速，vr為兩個相互移動節點間的相對運動速度。在本文中，vr即為發射機與接收機之間的徑向速度。

要計算軌道上vr，需要先確定軌道的參數，根據開普勒方程來確定衛星軌道位置和速度。當衛星軌道周期未給出時，根據開普勒定律，可得：

其中，K為開普勒常數，G為引力常量，M為地球質量，a為軌道長半軸。

衛星半徑矢量r是從地心到衛星的距離。當衛星沿軌道移動時，該值會隨式（4）變化：

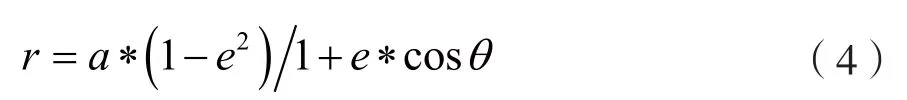
根據式（2）可得，衛星在軌道上的高度隨著時間的改變也在不斷變化，其到地球表面的距離r0也在不斷變化。衛星沿軌道運行到地面的距離表達式為：

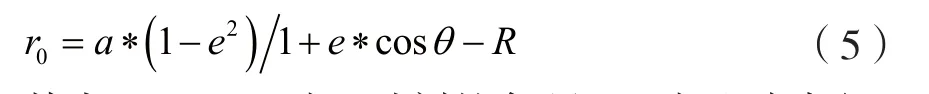
其中，θ=w×t為t時刻的角距；R為地球半徑；a為衛星軌道的長半軸；e為偏心率。

與此對應的衛星在t時刻的徑向速度表達式為：

由式（1）～式（6），聯立推導，可得多普勒頻移fd隨時間t的變化表達式：

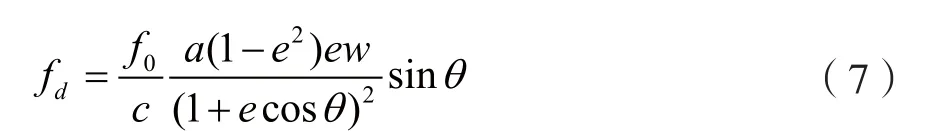
此外，傳統方法求vr的表達式為：

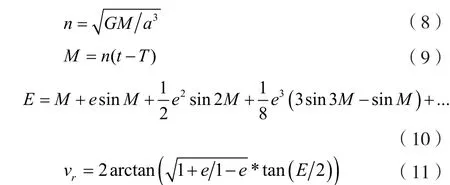
由式（8）～式（11）可得，傳統求解兩個相互移動節點間的相對運動速度vr時，需要先對E進行求解，而求解E的計算公式是一個無窮公式。對比傳統算法的無窮公式可知，本文方法在計算相對速度vr時，巧妙利用長半軸﹑偏心率等參數來計算，避免了求解無窮項公式，其復雜度遠小于傳統算法。

2 仿真結果及分析

本節將給出高橢圓軌道和中橢圓軌道某星的鏈路多普勒頻移的仿真結果。仿真步長為10 s，軌道的基本軌道參數如表1所示。地球半徑設為6 370 km，載波頻率為L-頻段取1.6 GHz。

表1 高橢圓軌道和中橢圓軌道的軌道參數

由圖1中衛星曲線可知，兩衛星的速度和距離都是周期變化的。高橢圓軌道距地面最大和最小距離分別是5.349×104km和3.075×104km，最大速度為1.151×104km/h；中橢圓軌道距地面最大和最小距離分別是1.888×104km和6 708 km，其最大速度為1.187×104km/h。

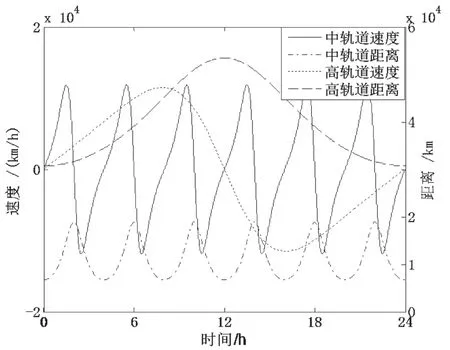
圖1 衛星速度與距離隨時間變化的曲線

如圖2﹑圖3所示，分別為運用傳統算法和所提算法得到的中橢圓軌道衛星在L-頻段下的多普勒頻移曲線。相對于圓軌道所得到的正弦變化，橢圓軌道的多普勒頻移呈現類正弦變化。對比兩曲線可見，所提算法的曲線和傳統算法的曲線存在一些微小差別，即所提算法的多普勒頻移誤差在0.056～0.070 3之間。這是由于在計算相對速度時，傳統算法的計算公式更加復雜，因此所得結果更加精確。在中軌道下，所得的兩條曲線總體趨勢與多普勒頻移變化范圍一樣。相比于頻移的數值，所提算法的頻移誤差可忽略不計。這也驗證了所提算法在理論上的有效性。

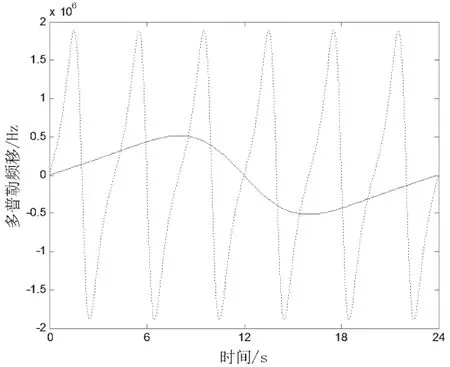
圖2 傳統算法在L-頻段載波多普勒頻移曲線

圖3為所提算法在L-頻段載波多普勒頻移曲線。由圖3可知：隨著衛星在橢圓軌道上運動，其速度在近地點最快，多普勒頻移也達到峰值；在遠地點最慢，多普勒頻移最小，其在中軌道上的頻移變化范圍是-17.59～17.59 kHz。對于中橢圓軌道衛星，由于其在軌道上運動速度快，速度變化快，所以其多普勒頻移變化范圍大，變化率大，造成載波同步和包絡檢測的困難，對接收機的解調性能要求較高。

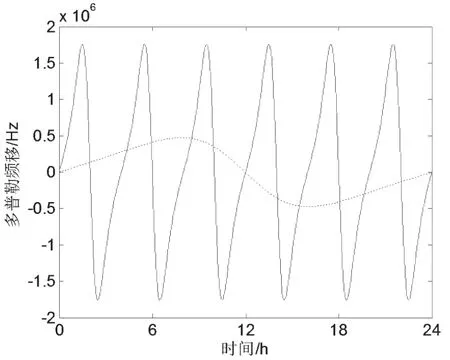
圖3 所提算法在L-頻段載波多普勒頻移曲線

實際情況下，衛星與地面站間存在相對運動，地面站與衛星并不是全部時間都處在連通狀態。為了驗證所提算法在實際情況下多普勒頻移曲線的有效性，建立一個實際模擬衛星與地面站之間通信模型，并計算衛星在中橢圓軌道下的頻移曲線，如圖4所示。

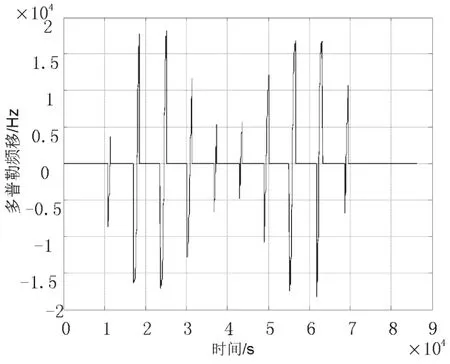
圖4 星地相對運動下的多普勒頻移曲線

在一晝夜里，衛星與地面站之間共通信10次，且由于兩者的相對運動導致每次通信的時間長短各不相同。由圖4可知：它的曲線是圖3中橢圓軌道曲線的一部分。這就驗證了本算法在實際場景中的有效性。

在其他條件不變的情況下，對比兩種算法在計算多普勒頻移時所耗的時間，以此驗證所提算法在計算復雜度上的優勢。如圖5所示，在同一個平臺下，隨著橢圓軌道周期的變化，兩種算法所耗時間均隨著周期的增大而增加。其中，本文所提算法所用時間小于傳統算法，說明其復雜度得到明顯簡化。

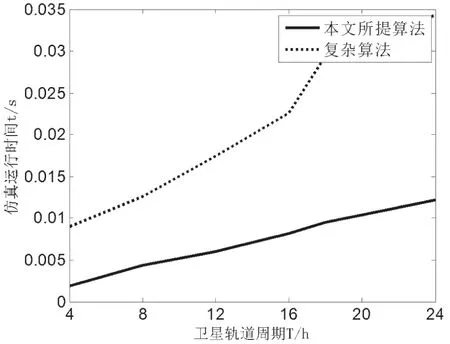
圖5 兩種算法運行所需時間對比曲線

3 結 語

本文主要提出了基于長半軸﹑偏心率﹑載波頻段等參數估算多普勒頻移的計算方法，并在理論仿真與實際場景中均驗證了其有效性。與傳統算法所耗時間相比，證明了證其在計算復雜度上的優勢。同時，分析高橢圓軌道和中橢圓軌道衛星通信鏈路的多普勒頻移特點。由仿真可得：因中橢圓軌道較高橢圓軌道具有更高速率﹑更大角度變化率，故中橢圓軌道比高橢圓軌道具有更大多普勒頻移，多普勒頻移變化范圍也更大；而在同軌道下，偏心率越大，多普勒頻移也隨之越大。由此可得：橢圓軌道具有其獨特優勢，故該軌道對應的多普勒頻移在衛星星座設計﹑衛星組網通信等過程非常關鍵。

[1] H?keg?rd J E,Bakken T,Myrvoll T A.User Requirements for HEO SATCOM for ATM in High Latitudes[C]. Integrated Communications,Navigation and Surveillance Conference,2009:1-9.

[2] Amiri S,Mehdipour M.Accurate Doppler Frequency Shift Estimation for Any Satellite Orbit[C].Recent Advances in Space Technologies,2007:602-607.

[3] Capuano V,Botteron C,Farine P A.GNSS Performances for MEO,GEO and HEO[C].Space Communications and Navigation Symposium-Space-Based Navigation Systems and Services,2013.

[4] 張雅聲,張育林.一種有效的中橢圓軌道衛星星座設計與分析[J].裝備指揮技術學院學報,2006,17(04):42-47.

ZHANG Ya-sheng,ZHANG Yu-lin.Design and Analysis of an Effective Medium Elliptical Orbit Satellite Constellation[J]. Journal of the Institute of Command and Control Technology,2006, 17(04):42-47.

[5] 張雅聲,姚勇.異構預警衛星星座設計與分析[J].裝備指揮技術學院學報,2009,20(03):47-51.

ZHANG Ya-sheng,YAO Yong.Design and Analysis of Heterogeneous Early Warning Satellite Constellation[J]. Journal of the Institute of Command and Control Technology,2009,20(03):47-51.

[6] Tsimbal M,Panko S.Features of the HEO Satellite Communication Systems[C].Control and Communications (SIBCON),2015 International Siberian Conference on. IEEE,2015:1-3.

[7] 王克鋒,何翔宇,趙洪利.衛星星間鏈路多普勒頻移仿真[J].無線電工程,2008,37(03):36-38.

WANG Ke-feng,HE X iang-yu,ZHAO Hong-li. Doppler Frequency Shift Simulation of Satellite Inter-Satellite[J].Radio Engineering,2008,37(03):36-38.

[8] Katayama M,Ogawa A,Morinaga N.Carrier Synchronization under Doppler Shift of the Nongeostationary Satellite Communication Systems[M].[Proceedings] Singapore ICCS/ ISITA92,1992.

[9] You M H,Lee S P,Han Y.Adaptive Compensation Method Using the Prediction Algorithm for the Doppler Frequency Shift in the LEO Orbit Mobile Satellite Communication System[J].ETRI Journal,2000,22(04):32-39.

[10] 張立巍,朱立東,吳詩其.橢圓軌道編隊小衛星星間鏈路幾何特性研究[J].電子與信息學報,2006,28(05):861-864.

ZHANG Li-wei,ZHU Li-dong,WU Shi-qi.Geometric Characteristics of Small Satellites Inter-satellite Link in Elliptical Orbit Formation[J].Journal of Electronics & Information Technology,2006,28(05):861-864.

[11] PENG G,HUANG Z,LI Q,et al.Dopp ler FrequencyShift Estimation and Compensation for LEO and MEO Satellite Signals[J].Systems Engineering and Electroni cs,2009,31(02):256-260.

[12] Draim J,嚴拱添.中高度橢圓軌道星座:一種提高多衛星系統成本效益的途徑[J].控制工程,1999,5(05):25-32.

DRAIM J,YAN Gong-tian.MediuMand High Elliptical Orbit Constellation:A Way to Improve the Costeffectiveness of Multi-satellite Systems[J].Control Engineering,1999,5(05):25-32.

Faster Estimation and Analysis of Dopp ler Frequency Shift from M edium Elliptic Orbit Satellites

QIAO Wen-long1, ZHANG Jian-wu1, BAO Jian-rong1,2, JIANG Bin1

(1.School of Communication Engineering, Hangzhou Dianzi University, Hangzhou Zhejiang 310018, China; 2.School of Information Science & Engineering, Southeast University, Nanjing Jiangsu 210096, China)

In satellite communications, the high-speed movement, the rapid angle change and some other factors of between the satellites and the ground stations would usually, cause fairly large Doppler frequency shifting, spectrum spreading, and other phenomena, thus deteriorating the satellite-ground communication performance. Based on the Doppler frequency shift algorithm under the Walker constellation a modified calculation method of the Doppler shift in the medium elliptical orbit satellite is proposed. Compared with traditional formula methods needing to know three-dimensional coordinates of the satellites in space, the computational complexity is greatly reduced through directly calculating the radius of the satellite by the semi-major axis of ellipse, eccentricity and other parameters. Finally, simulation comparison and analysis of the Doppler frequency shift curves in high elliptical orbit communication satellites fairly interprets the characteristics of medium elliptical orbit Doppler frequency shift. In addition, simulation on the characteristics of medium elliptical orbit Doppler frequency shift for the relative motion of between satellite and ground station indicates the effectiveness of this algorithm. All these could facilitate the rapid estimation of Doppler frequency shift and effectively support the signal reception in actual satellite communications.

satellite communication; medium ellipse orbit; link communication; doppler frequency shift

TN911.22

A

1002-0802(2016)-11-1442-05

10.3969/j.issn.1002-0802.2016.11.006

喬文龍（1990—），男，碩士，主要研究方向為通信信號處理等；

章堅武（1961—），男，博士，教授，主要研究方向為移動通信﹑個人通信等；

包建榮（1978—），男，博士，副教授，主要研究方向為通信信號處理等；

姜 斌（1980—），男，碩士，高級實驗師，主要研究方向為無線通信﹑信道編碼等。

2016-07-09；

2016-10-11 Received date:2016-07-09;Revised date:2016-10-11

浙江省自然科學基金重點項目（No.LZ14F010003）；國家自然科學基金（No.61471152）；東南大學移動通信國家重點實驗室開放研究基金（No.2014D02）；浙江省公益性技術應用研究計劃（No.2015C31103）

Foundation Item:Zhejiang Provincial National Natural Science Foundation(No.LZ14F010003);National Natural Science Foundation of China(No.61471152);Open Research Fund of National Mobile Communications Research Laboratory Southeast University(No. 2014D02);Zhejiang Provincial Science and Technology Plan Project(No.2015C31103)