基于子結構導納法的UUV發動機本體參數化建模研究

韓 飛， 王敏慶

(西北工業大學 動力與能源學院，西安市 710072)

基于子結構導納法的UUV發動機本體參數化建模研究

韓 飛， 王敏慶

(西北工業大學 動力與能源學院，西安市 710072)

為實現UUV發動機本體結構的參數化建模，基于模態分析結果以及外部激勵特性，建立子結構等效模型。根據能量守恒原理以及導納功率流的定義計算了各子結構的等效線導納，根據邊界連續條件確定耦合結構振動方程，最終建立了發動機本體振動傳遞參數化模型，計算了發動機本體不同位置處的輸入導納;通過試驗對模型的有效性進行了驗證。以發動機本體所受激勵作為輸入，根據所建模型開展了參數影響分析，結果表明：在400 Hz～1.8 kHz頻段內，氣缸軸向力以及滾輪切向力對艙段殼振動響應的貢獻較大,建模中需要考慮發動機不同方向上的振動傳遞特性；增大擺盤箱端蓋厚度能夠顯著降低艙段殼的振動響應。

振動傳遞；子結構；機械導納；參數化建模

擺盤發動機具有結構緊湊、比功率大等顯著特點，是目前無人水下航行器(Unmanned Underwater Vehicle, UUV)動力系統中廣泛采用的發動機型式。在水下低速航行時，由發動機工作產生的激勵載荷直接作用于發動機本體，引起氣缸體及擺盤箱的振動，這一振動能量經前、后隔振圈傳遞至發動機艙殼體，激起發動機艙殼體的彎曲振動，振動沿軸向傳遞至其他艙段殼體，進而引起結構的機械噪聲，是UUV輻射噪聲的主要來源之一。目前有關UUV結構的聲振特性研究已取得大量研究成果[1-6]，但圍繞發動機振動特性開展的研究工作仍然較少。由于發動機結構形式非常復雜，采用有限元方法進行研究時，為了提高分析頻率上限，通常會犧牲發動機結構的建模精度；統計能量分析方法受模態密度的限制，難以對幾何尺度較小的結構進行精確建模，對于結構低頻振動的分析結果存在一定誤差。在發動機結構的簡化建模方面，研究者一般將發動機等效為集中質量或將其附加在動力艙段的隔板上，這些簡化建模方式對于發動機結構的徑向振動特性影響較小。發動機結構不僅受到徑向激勵力，還受到軸向、切向等多種外部激勵，如能從結構振動的源頭入手，在同時考慮發動機本體在不同方向上的振動傳遞特性的基礎上，建立發動機本體的振動傳遞參數化計算模型，對于UUV結構減振降噪研究具有十分重要的意義。

子結構導納法[7]物理概念明確，能夠很好地反映結構內部和結構之間的振動能量傳遞特性，且不受分析頻段及已知中間參數等條件的限制。本文根據發動機本體的模態分析結果以及外部激勵特性，對其進行子結構劃分并分別建立各子結構等效模型，根據邊界連續條件構建耦合振動方程，最終建立發動機本體振動傳遞參數化計算模型，求解寬頻帶內各類激勵下的機械導納參數，代入至動力艙耦合結構中，以發動機本體結構所受外部激勵作為輸入條件開展參數影響分析，為UUV結構減振降噪設計提供參考。

1 理論模型

1.1 子結構劃分及等效模型

梁躍等[8]建立了發動機機體的3D實體模型，并借助有限元分析軟件開展了約束模態和自由模態分析，結果表明：發動機的振動特性主要表現為整體結構的彎曲、扭轉振動以及氣缸體端蓋、擺盤箱箱體和擺盤箱端蓋的局部彎曲振動，而氣缸體的缸體部分的振動并不明顯。基于發動機本體不同部位所呈現的振動特性差異，可將發動機本體初步劃分為四個子結構，分別為氣缸體端蓋、缸體以及擺盤箱箱體、端蓋。

另一方面，發動機本體是動力艙內振動傳遞路徑中的關鍵環節，受力情況比較復雜，在各子結構的不同部位受到多個方向的激勵，這些激勵不僅包含直接作用在發動機本體上的外部激勵，還包括發動機本體與其他結構之間的耦合作用力，見表1。

表1 發動機本體所受外部激勵

各子結構的等效模型在能夠反映實際結構振動特性的同時，還需滿足能夠施加各種激勵載荷的要求，綜合考慮最終建立各子結構的等效模型見圖1，采用圓板模型對氣缸體端蓋、擺盤箱端蓋進行等效建模，采用集中質量模型對缸體建模，采用圓柱殼模型對擺盤箱箱體建模。

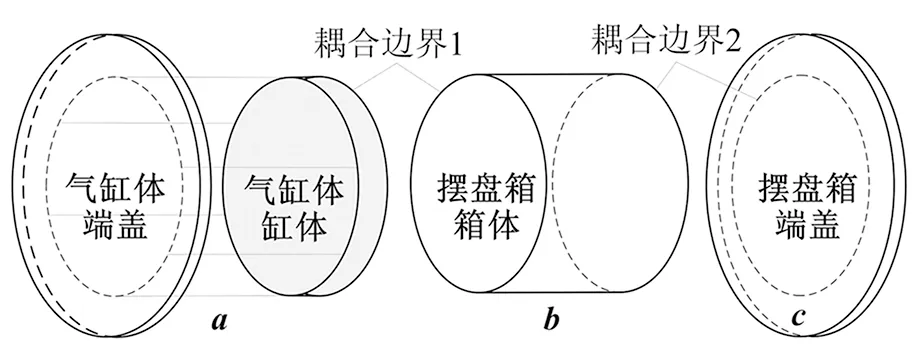
圖1 發動機本體等效模型

鑒于氣缸體的缸體部分振動特性單一，與氣缸體端蓋在耦合系統中為并聯關系[9]，為簡化耦合振動方程，本文最終將發動機本體結構劃分為三個子結構：氣缸體a、擺盤箱箱體b以及擺盤箱端蓋c。等效模型中去除了實際結構中存在的凸臺、安裝孔等細節特征，并保證主體尺寸與實際結構基本一致，具體參數取值為：氣缸體端蓋厚度ha=20 mm、氣缸體與擺盤箱端蓋半徑rac=218 mm、擺盤箱端蓋厚度hc=30 mm、擺盤箱箱體厚度hb=16 mm、擺盤箱箱體軸向長度lb=320 mm、擺盤箱箱體半徑rb=150 mm；各子結構的材料參數與實際結構保持一致。等效模型在較大程度上保留了實際結構的主要振動特性，但二者仍會存在一定差異，這種差異在理論分析中難以避免。

1.2 子結構機械導納

在發動機本體中，各子結構間均為線連接，基于能量守恒及功率流定義，可以通過式(8)計算得到各子結構的等效線機械導納[10]

(1)

式中:L1、L2分別為激勵線L1與響應線L2的長度，Y(x2,y2|x1,y1)表示由激勵線上點(x1,y1)到響應線上一點(x2,y2)的傳遞點導納，g1(x1,y1)與g2(x2,y2)分別表示激勵線與響應線上力的分布型函數。

根據圓板及圓柱殼等典型結構在受到不同方向點激勵情況下的振動響應，可以得到各子結構的機械點導納，推導過程參見文獻[11]，代入式(1)計算等效線導納。

1.3 耦合振動方程

在理論建模中，假設各子結構的彎曲振動與面內振動相互獨立。擺盤箱箱體的受力情況如圖2所示。

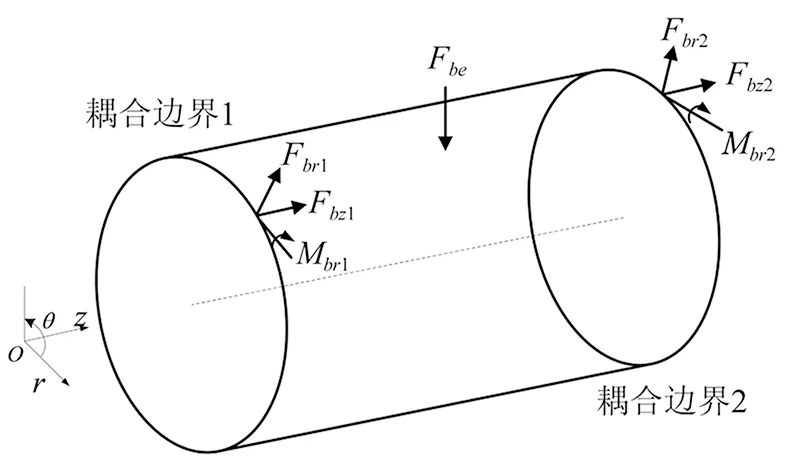
圖2 擺盤箱箱體受力示意圖

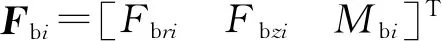
在耦合邊界1處，氣缸體的振動響應可以表示為

ua=AeFae+AFa

(2)

式中:Ae和A分別表示Fae和Fa對應的3×3階機械導納系數矩陣。

擺盤箱箱體同時與氣缸體以及擺盤箱端蓋連接，其在耦合邊界1、耦合邊界2處的振動響應分別為

ub1=Be1Fbe+B11Fb1+B21Fb2

(3)

ub2=Be2Fbe+B12Fb1+B22Fb2

(4)

式中:Be1與Be2分別表示Fbe作用下在耦合邊界1、2處引起的振動響應所對應的3×3階機械導納系數矩陣；B11、B12分別表示Fb1激勵引起耦合邊界1、耦合邊界2處引起的振動響應對應的3×3階機械導納矩陣；B21、B22分別表示Fb2激勵引起耦合邊界1、2處引起的振動響應對應的3×3階機械導納系數矩陣。

在耦合邊界2處，擺盤箱端蓋的振動響應可以表示為

uc=CeFce+CFc

(5)

式中:Ce和C分別表示Fce和Fc2對應的機械導納系數矩陣。

根據各子結構在耦合邊界力與速度連續的邊界條件，得到

ua=ub1，Fa+Fb1=0

(6)

ub2=uc，Fb2+Fc=0

(7)

將式(2)～式(5)代入式(6)與式(7)中，得到耦合振動方程

(8)

由式(8)計算得到各子結構在耦合邊界處受到的耦合力，進而求解各子結構在任意位置處的振動響應，最終得到發動機本體結構的各類機械導納參數。

2 試驗驗證

為驗證模型的有效性，本文開展了發動機本體輸入導納測試試驗。測試系統見圖3。在計算機測試軟件中設置白噪聲激勵信號，由多通道分析儀發出，經功率放大器輸入至激振器并作用于發動機本體結構。通過阻抗頭拾取激勵位置處的力信號與加速度信號，傳遞至分析儀中通過力歸一化處理獲取結構的輸入導納。

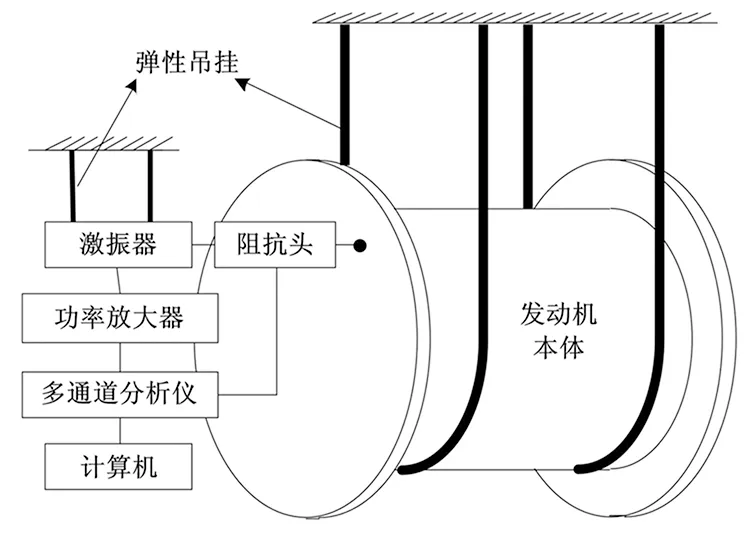
圖3 測試系統

在被測試件的激勵位置處黏貼磁片，并在阻抗頭端部安裝磁座，以此完成阻抗頭的安裝以及激振器對被測試件的激勵，見圖4。

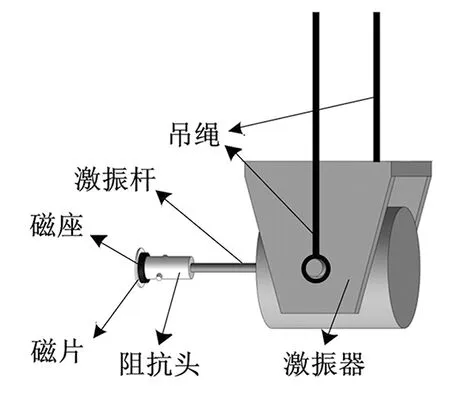
圖4 阻抗頭安裝示意圖

試驗測試中，通過激振器在發動機本體三個不同位置分別進行激勵：①在氣缸體端蓋施加軸向激勵力；②在擺盤箱箱體滾輪導槽施加切向激勵力；③在擺盤箱端蓋與斜軸對應的矩形槽施加軸向激勵力。

試驗測試了400 Hz～2 kHz頻段內發動機本體在上述三個激勵位置處的輸入導納，與本文模型計算結果對比見圖5～圖7，文中各圖所示機械導納曲線均為機械導納幅值。

由圖5～圖7所示各組對比曲線可知，本文模型計算所得機械導納曲線均值隨頻率變化的規律與試驗測試結果較為接近，能夠基本反映發動機本體受到不同位置外部激勵時的振動特性。由于理論等效模型無法完全逼近實際結構，導致計算結果與試驗結果存在一定差異，這種差異在理論分析中難以避免；另一方面，等效線機械導納參數本身就是經歷了多次“平均”后的結果，計算結果的均值水平更具參考價值。

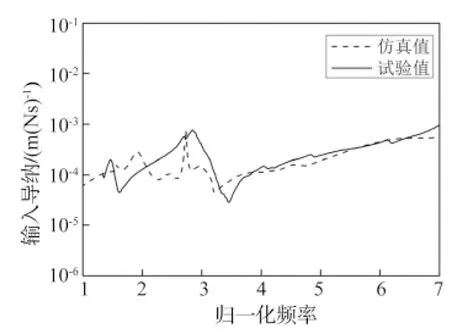
圖5 氣缸體端蓋軸向輸入導納

Fig.5 Axial input receptance of cylinder cap

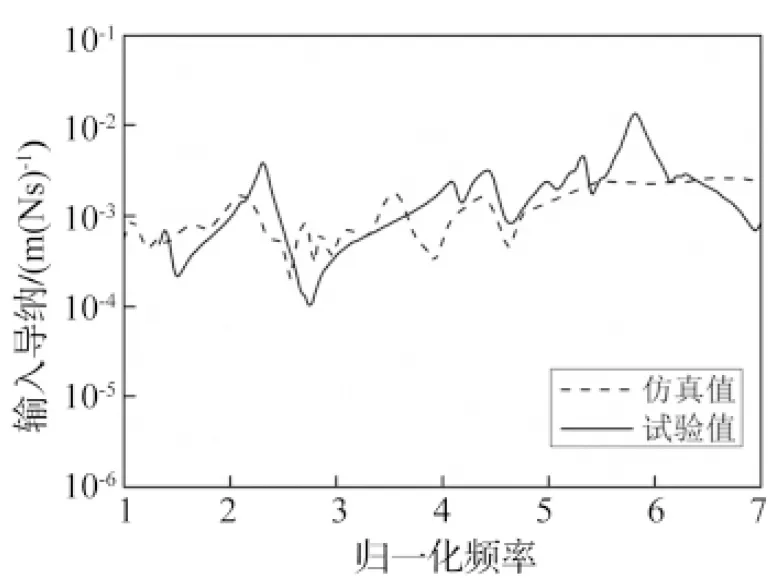
圖6 擺盤箱箱體切向輸入導納

Fig.6 Tangential input receptance of swashplate box body

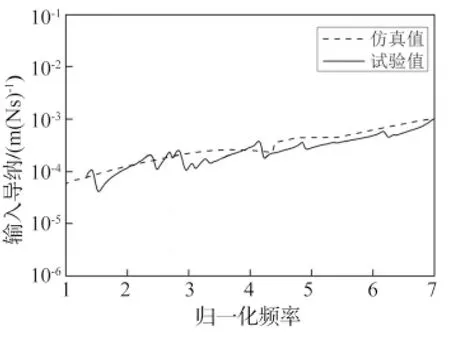
圖7 擺盤箱端蓋軸向輸入導納

Fig.7 Axial input receptance of swashplate box cap

3 仿真分析

工作狀態下發動機內部存在著不平衡的往復力與回轉慣性力，采用虛擬樣機技術對發動機結構進行動力學仿真分析[12-13]，計算得到某工況下400 Hz～1.8 kHz頻段內所受主要激勵載荷的頻譜特性見圖8，可以看出發動機本體受到的激勵力頻譜曲線呈現明顯的周期特性。將本文計算模型與前、后隔振圈以及艙段殼耦合建模，即可計算由發動機本體到艙段殼任意點的傳遞導納。將外部激勵代入至耦合結構計算模型，以艙段殼滑油口為目標點，分別計算各外部激勵單獨作用下以及合力作用下目標點處的振動響應，見圖9。為便于對比分析，本文將目標點振動響應的仿真結果以1/3倍頻程的形式給出。

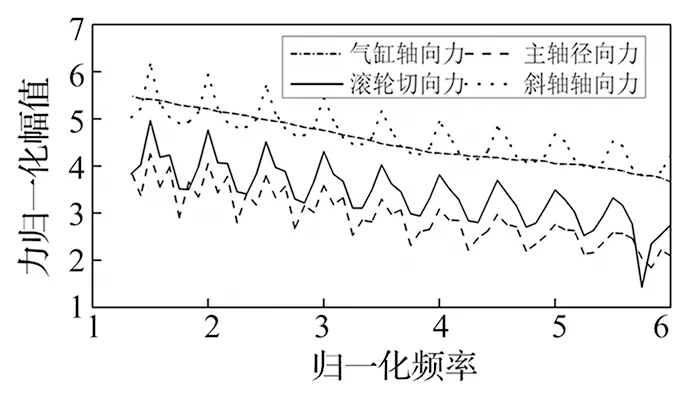
圖8 外部激勵載荷頻譜圖

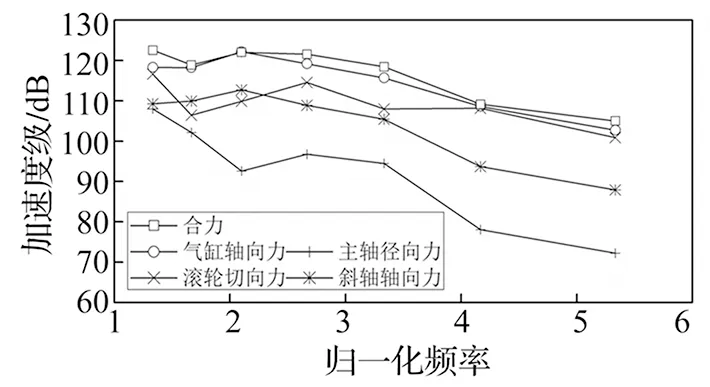
圖9 艙段殼振動響應

通常情況下艙段殼的彎曲振動主要由前、后隔振圈處的徑向耦合力及繞耦合邊界方向的彎矩激勵引起，因此在對發動機結構進行等效建模時通常只考慮其徑向振動傳遞特性。但是從圖9所示仿真結果可以看出，在400 Hz～1.8 kHz分析頻段內，氣缸軸向力對于艙段殼振動響應的貢獻最大，滾輪切向力以及斜軸軸向力次之，主軸徑向力在四個激勵力中貢獻最小。這說明發動機結構作為主要振動源，其內部的振動傳遞特性不可忽視，建模時需要充分考慮發動機本體不同方向上的振動傳遞特性，否則將會產生一定誤差。

根據本文所建發動機本體參數化模型，可以快速實現結構參數對耦合結構振動特性影響規律的研究。仿真分析中，依次改變氣缸體端蓋厚度，氣缸體與擺盤箱端蓋半徑、擺盤箱端蓋厚度、擺盤箱箱體厚度、擺盤箱箱體軸向長度以及擺盤箱箱體半徑，所得艙段殼振動響應對比曲線見圖10。

從圖10可知，增大擺盤箱端蓋的厚度能夠顯著降低艙段殼振動響應，但是增大氣缸體端蓋的厚度反而會使艙段殼的振動響應升高，小幅改變氣缸體與擺盤箱端蓋半徑對艙段殼振動水平幾乎沒有影響；增大箱體厚度或箱體半徑對降低艙段殼的振動水平也具有一定增益效果，但考慮到某些輔機的安裝條件，其徑向尺度參數的變化范圍受到一定限制；改變箱體軸向長度會使箱體彎曲振動的固有頻率在不同分析頻段內分布情況發生較大改變，其影響規律較為復雜。

分別改變氣缸體、擺盤箱的材料參數，參數取值見表2，仿真計算所得艙段殼振動響應見圖11。

圖10 幾何參數對艙段殼振動響應的影響Fig.10 Geometric parameter’s influence to vibration response of cabin shell

表2 材料參數

從圖11(a)、圖11(b)所示對比曲線可知，擺盤箱材料參數對于艙段殼振動響應的影響要高于氣缸體材料參數，僅就表2中材料而言，選取楊氏模量及密度相對較大的材料2，其對應的艙段殼振動總能級較低。對比圖11(b)圖11(c)所示曲線，材料楊氏模量對于艙段殼振動水平的影響高于材料密度，選取密度較大但楊氏模量不同的兩種材料分別作為氣缸體、擺盤箱的選材有助于降低發動機本體傳遞到艙段殼的振動能量。由于密度改變會對UUV結構的重心位置產生較大影響，因此參數優化設計需要與穩定性設計聯合開展。

4 結 論

本文運用子結構導納法建立了UUV發動機本體振動傳遞參數化計算模型，計算了不同位置處的輸入導納，與試驗測試結果進行了比對，并以外部激勵作為輸入條件，分析了400 Hz～1.8 kHz頻段內參數改變對耦合結構振動特性的影響規律，所得主要結論如下

(1)本文模型能夠計算多種激勵力作用下發動機本體在不同方向上的輸入導納，計算結果與試驗測試結果變化趨勢基本一致。

(2)氣缸軸向力以及滾輪切向力對艙段殼振動響應的貢獻較大，在動力艙段耦合結構的振動傳遞特性研究中，需要考慮發動機不同方向上的振動傳遞特性。

(3)增大擺盤箱端蓋厚度能夠顯著降低由發動機振動引起的艙段殼振動響應。

[ 1 ] 何惠江, 李楠. 基于APDL的魚雷殼體結構參數化建模[J]. 魚雷技術, 2010, 18(4): 246-248. HE Huijiang, LI Nan. Parametric modeling of torpedo shell structure based on APDL[J]. Torpedo Technology, 2010, 18(4): 246-248.

[ 2 ] 曹銀萍, 石秀華. 基于ANSYS的魚雷有限元建模與模態分析[J]. 彈箭與制導學報, 2009, 29(3): 289-292. CAO Yinping, SHI Xiuhua. Finite element modeling and modal analysis of torpedo based on ANSYS[J]. Journal of Projectiles, Rockets, Misseles and Guidance, 2009, 29(3): 289-292.

[ 3 ] 秦曉輝, 尹韶平. 統計能量分析在魚雷結構振動及聲輻射研究中的應用[J]. 魚雷技術, 2006, 14(1): 24-27. QIN Xiaohui, YIN Shaoping. Application of statistical energy analysis to structure vibration and sound radiation of torpedo[J]. Torpedo Technology, 2006, 14(1): 24-27.

[ 4 ] 丁少春, 朱石堅, 樓京俊. 魚雷結構振動與聲輻射的統計能量分析[J]. 浙江大學學報(工學版), 2009, 43(7): 1222-1224. DING Shaochun, ZHU Shijian, LOU Jingjun. Statistical energy analysis on structure vibration and sound radiation from torpedo[J]. Journal of Zhejiang University(Engineering Scicene), 2009, 43(7): 1222-1224.

[ 5 ] 劉凱, 朱石堅, 丁少春. 基于AutoSEA的魚雷結構輻射噪聲預報方法[J]. 魚雷技術, 2010, 18(2): 91-94. LIU Kai, ZHU Shijian, DING Shaochun. A prediction method for structural noise radiation of torpedo based on auto SEA[J]. Torpedo Technology, 2010, 18(2): 91-94.

[ 6 ] 馬銳磊, 尹韶平, 曹小娟, 等. 基于FEM的魚雷低頻振動環境預示方法研究[J]. 艦船電子工程, 2014, 34(5): 136-139. MA Ruilei, YIN Shaoping, CAO Xiaojuan, et al. Torpedo’s vibration environment prediction method of low frequency based on FEM[J]. Ship Electronic Engineering, 2014, 34(5):136-139.

[ 7 ] CUSCHIERI J M. Structural power-flow analysis using a mobility approach of an L-shaped plate[J]. Journal of the Acoustical Society of America, 1990, 87(3): 1159-1165.

[ 8 ] 梁躍, 何長富, 彭博. 魚雷熱動力發動機機體振動模態分析[J]. 魚雷技術, 2005, 13(4):18-20. LIANG Yue, HE Changfu, PENG Bo. Srtuctural vibration modal analysis of torpedo thermal power engine[J]. Torpedo Technology, 2005, 13(4):18-20.

[ 9 ] 阿·斯·尼基福羅夫. 船體結構聲學設計[M]. 謝信, 王軻,譯. 北京: 國防工業出版社, 1998.

[10] 趙芝梅, 王敏慶. 板殼結構振動功率流的子結構線導納法研究[J]. 工程力學, 2012, 29(8):294-301. ZHAO Zhimei, WANG Minqing. A structure line receptance method for analysis of power flow in a clylindrical shell with a floor partition.[J] Engineering Mechanics, 2012, 29(8):294-301.

[11] SOEDEL W. Vibration of shells and plates[M]. New York: Marcel Dekker, 1993.

[12] 李鑫, 王志剛, 萬榮華, 等. 基于虛擬樣機技術的魚雷周轉斜盤發動機動力學分析[J]. 魚雷技術, 2011, 19(4): 285-289. LI Xin, WANG Zhigang, WAN Ronghua, et al. Dynamic analysis of torpedo swashplate engine based on virtual protoyype technology[J]. Torpedo Technology, 2011, 19(4): 285-289.

[13] 張進軍, 楊杰，錢志博. 基于虛擬樣機技術的擺盤發動機仿真[J]. 計算機仿真, 2012, 29(4):328-332. ZHANG Jinjun, YANG Jie, QIAN Zhibo. Simulation of swashplate engine based on virtual prototyping technology[J]. Computer Simulation, 2012, 29(4):328-332.

Parametricmodeling of UUV engine body based on substructure receptance method

HAN Fei, WANG Minqing

(School of Power and Energy, Northwestern Ploytechnical University, Xi’an 710072, China)

To acquire a parametric model of UUV engine body, based on modal analysis results and external excitation characteristics, the equivalent model of its each substructure was established and their line receptances were calculated based on the principle energy conservation and the definition of mobility power flow. According to boundary continuity conditions, the coupling vibration equations between substructures were established, and finally, a vibration transfer parametric model of UUV engine body was obtained. The input receptances at different positions of the engine body were calculated. The model was validated with mechanical receptance tests. Taking external excitations as inputs, the influences of some major parameters of the model were analyzed. Results showed that in the range of 400Hz～1.8kHz, the axial force applied on cylinder block and the tangential force of rolling wheel make major contribution to the vibration response of cabin shell; the vibration characteristics of the engin body in different directions need to be considered in engine modeling; increasing the thickness of swing tray box’s end cover can significantly reduce the vibration response of cabin shell.

vibration transmission; substructure; mechanical receptance; parametric modeling

2015-09-04 修改稿收到日期：2015-11-30

韓飛 男，博士生，1988年生

王敏慶 男，博士生導師，1970年生

O327；TB532