老城區道路交通健康狀態評價體系研究

汪春

（合肥工業大學建筑設計研究院,安徽 合肥 230041）

老城區道路交通健康狀態評價體系研究

汪春

（合肥工業大學建筑設計研究院,安徽 合肥 230041）

根據老城區道路交通健康狀態評價準則，構建評價指標體系，從易采集、易量化、可比性、綜合性等方面權衡，選取道路網絡密度、公交站點覆蓋率、自行車網絡密度、步行網絡密度4個指標，評價方法上采用了擴展性較好的線性模型，并通過層次分析法和專家決策法，求解各評價指標權重系數。通過老城區道路交通健康狀態評價體系，可以快速對老城區道路交通健康狀態進行評價。老城區道路交通健康狀態評價體系是一種老城區城市規劃建設管理工具，目的是建立一套老城區道路交通評價體系，評價老城區道路交通在多重因素作用下發展狀態和發展趨勢，通過直觀和量化手段對老城區交通健康狀態橫向比較、縱向比較，便于進行問題分析和查找。

健康城市；老城區；道路交通；評價體系

0 引言

隨著城市不斷發展，城市病在全球城市逐步顯現，老城區更是首當其沖。從20世紀80年代開始，基于城市病治理的健康城市理念從公共衛生領域快速擴展到城市規劃領域，從北美、歐洲開始席卷全球[1]。構建健康老城區，其中首要問題是系統解決老城區交通問題，構建老城區健康道路交通體系，并提出一套便于操作的老城區道路交通健康狀態評價體系。

國內外對于健康城市交通規劃、健康城市道路交通的相關研究較少，針對老城區健康道路交通特征的研究沒有涉及，且尚未提出老城區道路交通系統健康狀態評價體系[2]。

老城區道路交通健康狀態是一種老城區城市規劃建設管理工具，目的是建立一套老城區道路交通評價體系，評價老城區道路交通在多重因素作用下發展狀態和發展趨勢。現狀對老城區道路交通評價，主要從道路網絡、公交系統、慢行系統等子系統進行獨立評價，健康道路交通狀態評價需要尋求較為完善的評價體系，對老城區道路交通進行綜合評價。如何建立評價體系，是老城區道路交通健康狀態評價的核心問題。

1 評價指標體系

評價老城區道路交通健康狀態需要有一套明確的量化指標，老城區道路交通健康狀態評價的核心是建立評價指標體系，是評價結果可信度的關鍵因素。評價指標體系選擇一方面要全面反映老城區道路交通狀況，另一方面又要方便獲取、便于計算。

1.1 評價指標體系

老城區道路交通健康狀態強調以人為本、綠色低碳，因此更關注公共交通、慢行交通相關評價指標。綜合全面性、易獲取、易量化等方面因素，本論文選道路網密度、公交站點覆蓋率、非機動車道網絡密度、步行網絡密度4項指標，構成本論文評價指標體系。下一步隨著研究深入，對指標體系可進一步擴展[3]。

1.1.1 道路網密度

道路網絡是老城區道路交通載體，是老城區道路交通最重要限制因素。道路網絡密度決定著老城區交通容量，也是現狀老城區交通核心問題所在。道路網密度一方面能反映老城區道路網建設水平，另一方面能反映老城區布局均衡和合理性，十分適合作為老城區道路交通健康狀態主要評價指標之一。

1.1.2 公交站點覆蓋率

公共交通最能體現老城區以人為本、綠色低碳特征，其發展水平直接關系到老城區道路交通健康狀態。評價老城區公共交通發展水平，公交站點覆蓋率是最為常見的評價指標。公交站點覆蓋率通常分為300 m和500 m半徑，是指所有公交站點在計算服務半徑下覆蓋面積之和與城區面積的比值，指標即體現了公交服務覆蓋的面積，又反映公交為居民提供服務的便捷程度，適宜作為老城區道路交通健康狀態評價指標。

1.1.3 自行車道網絡密度

自行車曾經是老城區主要交通方式之一，近年來隨著健康環保、綠色低碳理念，自行車迎來了全面復興。自行車交通作為一種健康交通方式，對老城區道路交通健康狀態影響較大。作為老城區自行車交通方式硬件支撐，自行車道網絡密度應納入老城區道路交通健康狀態評價指標體系中。

1.1.4 步行網絡密度

老城區商業設施集中、建筑密集，步行是老城區最為普遍和有效的交通方式，是老城區保持街道活力的重要因素，也是最為健康的交通方式。步行網絡密度是反映老城區步行服務水平重要指標之一，因此將其納入老城區道路交通健康狀態評價指標體系。

1.2 評價指標量化和標準體系

可比性、可量化、易量化是評價指標選取重要原則，在老城區道路交通健康狀態評價指標體系構建過程中也充分考慮這一原則。

《城市交通管理評價指標體系（2012版）》建立了一整套指標評價標準，本論文所選取4個評價指標均包括在內，因此本論文評價標準參照《城市交通管理評價指標體系（2012版）》[4]。另外在《城市道路交通規劃設計規范》（GB 50220—1995）中對本論文所選取的4個評價指標計算方法均有明確說明，可以方便計算得到。

根據評價標準體系，4個評價指標分值量化見表1。

2 老城區道路交通健康狀態評價方法

老城區道路健康狀態評價指標相對獨立，且評價模型要易于擴展，因此論文采用線性模型作為老城區道路交通健康狀態評價方法。

2.1 線性模型

線性模型是正態線性模型直接推廣，可適用于連續數據和離散數據。線性模型反映了自變量x1…，xk與因變量y之間的關系，通過觀察資料（yi，xi1，…，xik），i=1，2，…，n來探討這種關系是否存在，自變量x1…，xk的變化在多大的程度上對y的值有影響，有哪些自變量xi是重要的，哪些是不重要的。

用（A）*的寫法來描述線性模型，y是因變量的觀察向量，Xn×k是自變量的觀察向量組成的矩陣，線性模型就是

線性模型就是將（A）*中的條件放寬。若用μ表示y的期望值，由（A）*要求μ是x1，…，xk的線性函數，在線性模型中，引入連接函數g（μ），令

線性模型還把y是正態分布這一條件放寬為具有散度參數中的單參數指數族分布。由于上述兩個條件已放寬，（A）*中獨立同方差的條件自然也就放寬了，獨立性仍然保持，而方差可以改變。

線性模型用于老城區道路網健康狀態建模的基本形式見下式：

式中:I為綜合評判值,其值的高低表示老城區道路網的健康水平；Ai為i項指標的權重值；Yi為i指標的得分，i=1,2,3,4。

其中，Y1表示道路網密度得分，Y2表示公交站點覆蓋率得分，Y3表示非機動車道路網密度，Y4表示步行網絡密度。

2.2 權重計算

在線性模型中，由于缺乏回歸分析所需歷史數據，本論文采用層次分析法和專家決策法來確定權重系數[2]。

2.2.1 層次分析法

2.2.1.1 層次分析法原理

層次分析法（the analytic hierarchy process，AHP）是一種解決多目標復雜問題的決策分析方法，將定量分析與定性分析結合起來，用決策者的經驗判斷各衡量目標能否實現標準之間相對重要程度。

層次分析法大體可分為四個步驟。步驟一是建立層次結構模型，結構模型包括目標層、指標層和方案層；步驟二是構造兩兩比較的成對比較矩陣，成對比較矩陣是量化依據，是后序計算基礎，由于受人的主觀因素影響很大，應由經驗豐富、判斷力強的專家給出；步驟三是由成對比較矩陣計算被比較元素相對權重；步驟四是計算各層元素組合權重。

2.2.1.2 建立層次結構模型

老城區道路交通健康狀態評價目標層為老城區道路交通健康評分，指標層包括道路網密度、公交站點300 m半徑覆蓋率、自行車網絡密度、步行網絡密度4個指標，方案層為具體供評價的老城區。

2.2.1.3 構造判斷矩陣

老城區道路交通健康狀態評價重點是確定道路網密度、公交站點覆蓋率、自行車網絡密度、步行網絡密度相對于老城區道路交通健康狀態的權重。在確定指標層各指標之間權重時，定性給出結果不具備科學性，本論文采用著名運籌學家T.L. Santy提出的一致矩陣法，通過4個指標之間兩兩相互比較，構建判斷矩陣，用來表示4個指標針對老城區道路交通健康狀態相對重要性比較。判斷矩陣元素αij建議采用1～9比例標度法給出（見表2）。指標層指標個數可以根據所掌握數據情況進行擴展。

表2 矩陣元素αij標度方法表

根據老城區道路交通特點,對道路網密度A1、公交站點覆蓋率A2、非機動車道網絡密度A3、步行網絡密度A44項指標進行兩兩比較后，構建判斷矩陣：

構建完成后，需要對判斷矩陣進行一致性考察。判斷矩陣可以不一致，但需要在一個范圍之內。對于不一致的判斷矩陣，需要求解最大特征值和特征向量。Satty等人建議用對應于最大特征根λmax的特征向量，經歸一化后，作為權向量W，即如式（4）所示：

2.2.1.4 判斷矩陣一致性檢驗

W是指標層中4個指標對于老城區道路交通健康狀態相對重要性的排序權值，是層次單排序。層次單排序是否成立，需要對判斷矩陣A進行一致性檢驗。當判斷矩陣A具有一致性或偏離一致性程度在可接受范圍內時，W能反映各指標之間相對重要性程度，可以在健康狀態評價中加以應用。

當λmax比n大得越多時，A的不一致性越嚴重，因此用λmax-n的大小來衡量A的不一致程度，從而確定一致性指標CI，見式（5）。當CI＝0時，A有完全一致性，當CI越大，不一致越嚴重：

為衡量CI大小，引入隨機一致性指標RI，RI取值可以通過表3查詢得到。

表3 RI的取值

在CI和RI確定后，計算一致性比率，見式（6），當一致性比率CR＜0.1時，可認為判斷矩陣A的不一致程度在容許范圍之內，有滿意的一致性，通過一致性檢驗，其歸一化特征向量W可以作為權重向量，否則需要重新構造判斷矩陣A，直到通過一致性檢驗：

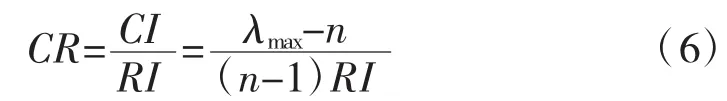
計算得到本次構造矩陣A的一致性比率CR=0＜0.1，為完全一致矩陣，滿足一致性要求，因此老城區道路交通健康狀態評價4項指標權重向量為

2.2.2 專家決策法

2.2.2.1 專家決策法介紹

專家決策法是一種向專家進行調查研究，依靠專家經驗和智慧進行集體判斷的方法，特別適用于在許多條件不確定時決策。專家決策法采用匿名方式通過多次函詢征求專家們意見，組織決策小組對每一輪意見進行匯總整理，作為參照資料再發給每一個專家，供他們分析判斷，提出新意見，多輪后專家意見漸趨一致，得到最終結論。

采用專家決策法時，決策專家一般應有名望或從事所調查專業多年，專家人數一般以20～50人為宜；宜反復進行三四輪調查，在專家意見趨于一致時，確定趨于一致的決策結果。在調查過程中要注意匿名性、反饋性和收斂性，匿名性可保證專家之間相互消極影響，反饋性可以讓每個人知道意見傾向，收斂性可以確保最終決策意見代表全體專家意見，是集體智慧結晶。

2.2.2.2 專家決策法計算指標權重系數

專家決策法計算方法很多，有加法評價、連積評價、和數相乘評價、加權評價、功效系數等多種方法。本論文4個評價指標之間關系簡單，且不涉及多方案評價，宜采用加法評價法，將每輪所調查專家對每一項指標權重的平均值作為本輪權重推薦值。

本論文通過向20位交通領域和城市規劃領域專家，進行3輪老城區道路網健康狀態影響因素權重問卷調查，第三輪調查表格整理見表4。

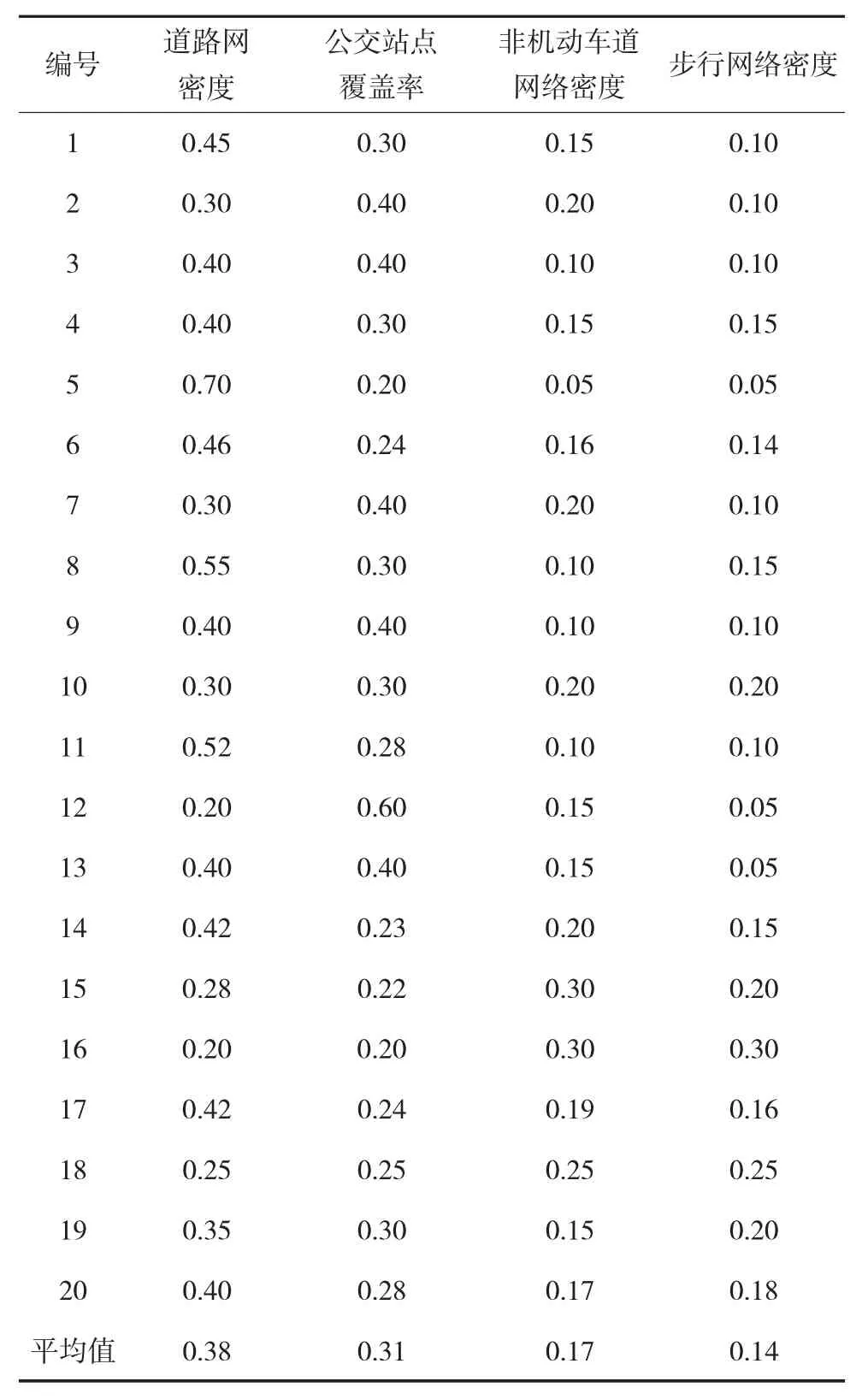
表4 專家決策法第三輪調查結果匯總表

將第三輪4項指標權重平均值作為專家決策法推薦權重，即4項指標權重向量為

2.2.3 模型權重系數確定

將層次分析法和專家決策法得到的老城區道路交通健康狀態4個影響指標權重系數進行平均后，得到4項指標權重向量為W=（0.38，0.28，0.18，0.16）T。

3 實例應用

3.1 現狀老城區道路交通健康狀態評價

老城區現狀道路網密度為4.17 km/km2，公交站點300 m覆蓋率為86.2%，非機動車道路網密度為8.44 km/km2，步行路網密度為9.31 km/km2。

由表5可得，老城區現狀路網密度得分Y1= 47.55，老城區現狀公交站點300 m覆蓋率得分Y2=96.55，老城區現狀非機動車道路網密度得分Y3=36.17，老城區現狀非機動車道路網密度得分為Y4=46.55。

由所建立的模型I=AiYi得，合肥市老城區現狀道路交通健康狀態最終得分為

I=47.55×0.38+96.55×0.28+36.17×0.18+ 46.55×0.16=59

3.2 改善后老城區道路交通健康狀態評價

對老城區進行規劃調整后，老城區規劃道路網密度為12.98 km/km2，公交站點300 m覆蓋率為99%，非機動車道路網密度為17.63 km/km2，步行路網密度為18.17 km/km2。

將論文研究成果在合肥市老城區交通改善研究中加以應用，分別針對合肥市現狀和改善后道路交通健康狀態進行評價。

表5 老城區道路網健康狀態影響指標量化得分指標

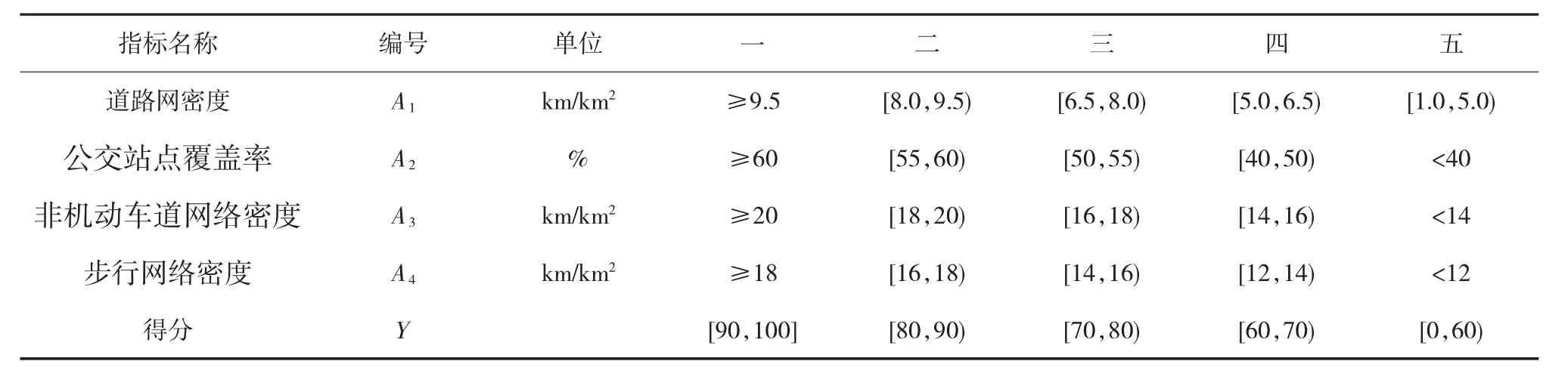
表6 老城區道路網健康狀態影響指標量化得分指標

由表6可得，老城區規劃路網密度得分Y1=97.27，老城區規劃公交站點300 m覆蓋率得分Y2=99.75，老城區規劃非機動車道路網密度得分Y3=78.15，老城區規劃非機動車道路網密度得分Y4=90.85。

由所建立的模型I=AiYi得，老城區規劃道路交通健康狀態最終得分為

I=97.27×0.38+99.75×0.28+78.15×0.18+ 90.85×0.16=93

對比分析可知，通過老城區健康交通規劃和設計后，老城區道路交通健康狀態有較大幅度提升，健康狀態得分由現狀59分提升為93分，規劃設計措施效果明顯。

4 結語

基于易使用、易擴展原則，本文構建了老城區道路交通健康狀態評價指標體系，包括道路網絡密度、公交站點覆蓋率、自行車道網絡密度和步行網絡密度四大指標，提出了老城區道路交通健康狀態評價線性模型，并通過層次分析法和專家決策法，對線性模型系數進行求解。通過評價體系，輸入相關參數，可以直觀、便捷地得到老城區道路交通健康得分。

[1]許從寶.健康城市與健康城市規劃——當代國際健康城市運動基本理論引介與研究[D].南京:東南大學,2006.

[2]楊濤.健康交通與健康城市[J].城市交通,2013,11(1):1-4.

[3]楊明,過秀成.老城區交通特征、問題解析與改善對策初探[J].現代城市研究,2012，27(4):82-86.

[4]陸建,王煒.面向可持續發展的城市交通系統綜合評價方法研究[J].土木工程學報,2004,37(3):99-104.

U491.1

A

1009-7716（2016）12-0143-05

10.16799/j.cnki.csdqyfh.2016.12.043

2016-08-26

汪春（1983-），男，安徽樅陽人，工程師，從事城市交通規劃、智能交通規劃設計工作。