偏序度量空間中混合單調隨機算子的耦合重合點定理

李承耕，許紹元，劉 波

(韓山師范學院數學與應用數學系，廣東 潮州 521041)

偏序度量空間中混合單調隨機算子的耦合重合點定理

李承耕，許紹元，劉 波

(韓山師范學院數學與應用數學系，廣東 潮州 521041)

研究了偏序度量空間中的隨機混合單調算子，并將一般混合單調算子的重合點定理擴展到隨機混合單調算子的耦合重合點定理，推廣了已有文獻的一些結論.

偏序；耦合重合點：混合單調算子；隨機算子

1 預備知識

混合單調算子是一類非常重要的算子，它于1987年由郭大鈞和Lakshmikantham[1-2]提出后，眾多學者對其做了大量研究，得到一批很好的結果.[2-9]它的很多理論已被應用于非線性微分方程與非線性積分方程解的存在性問題的研究中.本文在文獻[1-3]的基礎上，討論了兩類混合單調算子隨機耦合重合點問題，修改了文獻[3]給出的壓縮條件，并在新的壓縮條件下討論了隨機耦合重合點的存在性與唯一性問題，得到了與文獻[3]相區別的一些結論.

定義1[5]設(X，d)是一個偏序集，映射F:X×X→X和g:X→X滿足：(1) 若g(x1)≤g(x2)，則F(x1，y)≤F(x2，y)；(2) 若g(y1)≤g(y2)，則F(x，y2)≤F(x，y1).則稱算子F(x，y)具有混合g-單調性，即F(x，y)對x具有g-單調非減性，F(x，y) 對y具有g-單調非增性.

定義2[5]對于算子F:X×X→X和g:X→X，如果F(x，y)=g(x)，且F(y，x)=g(y)，則稱元素(x，y)為F對g的一個耦合重合點.

定義3[3]對于隨機算子F:Ω×(X×X)→X，若滿足：(1)?ω∈Ω，F(ω，·)連續；(2)?v∈X×X，F(·，v)可測.則稱F是連續隨機算子.

2 主要結果

設(X，≤)是一個偏序集，(X，d)是完備可分度量空間，(Ω，Σ)為可測空間，F:Ω×(X×X)→X和g:Ω×X→X為混合單調算子.本文做如下假設：

(A1)F(ω，·)和g(ω，·)是連續的，?ω∈Ω.

(A2)F(·，v)和g(·，x)是可測的，?v∈X×X，?x∈X.

(A3)F(ω×(X×X))?X，對每個ω∈Ω.

(A4)g是連續的，對F是可交換的.

(A5)F是連續的.

(A6)X滿足:如果一個非減序列xn→x，則xn≤x對任意的n成立；如果一個非增序列xn→x，則x≤xn對任意的n成立.

定理1 設(X，≤)是一個偏序集，(X，d)是完備可分度量空間，(Ω，Σ)為可測空間，F:Ω×(X×X)→X和g:Ω×X→X為混合單調算子.對任意α+β<1，α>0，β>0，ω∈Ω，不等式

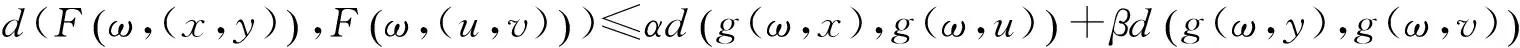
對所有滿足g(ω，x)≤g(ω，u)，g(ω，y)≥g(ω，v)的x，y，u，v∈X成立，且假設(A1)—(A6)成立.如果存在可測映射ξ0，η0∈X，使得g(ω，ξ0(ω))≤F(ω×(ξ0(ω)，η0(ω)))，F(ω×(η0(ω)，ξ0(ω)))≤g(ω，η0(ω))，則也存在可測映射ξ，θ:Ω→X，使得F(ω×(ξ(ω)，θ(ω)))=g(ω，ξ(ω))，F(ω×(θ(ω)，ξ(ω)))=g(ω，θ(ω))， ?ω∈Ω.即F和g存在耦合隨機重合點.

證明 設Θ={ξ|Ω→X}是一個可測映射類.定義函數h:Ω×X→R+，h(ω，x)=d(x，g(ω，x))，則由已知條件，h(ω，·)連續，h(·，x)可測，從而h(ω，x)是Caratheodory函數.故當ξ:Ω→X可測時，ω→h(ω，ξ(ω)) 也是可測的.?ξ∈Θ，定義η(ω)=g(ω，ξ(ω))，則η:Ω→X也是可測的，η∈Θ.

g(ω，ξ1(ω))=F(ω，(ξ0(ω)，η0(ω)))，g(ω，η1(ω))=F(ω，(η0(ω)，ξ0(ω)))，

這樣確定了ξ1，η1；再由F(ω，(ξ1(ω)，η1(ω)))∈X=g(ω×X)，F(ω，(η1(ω)，ξ1(ω)))∈X=g(ω×X)，存在ξ2，η2∈Θ使得

g(ω，ξ2(ω))=F(ω，(ξ1(ω)，η1(ω)))，g(ω，η2(ω))=F(ω，(η1(ω)，ξ1(ω)))，

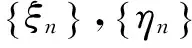
g(ω，ξn+1(ω))=F(ω，(ξn(ω)，ηn(ω)))，g(ω，ηn+1(ω))=F(ω，(ηn(ω)，ξn(ω))).

(1)

下面用數學歸納法證明

g(ω，ξn(ω))≤g(ω，ξn+1(ω))，g(ω，ηn(ω))≥g(ω，ηn+1(ω))，n≥0.

(2)

當n=0時，g(ω，ξ0(ω))≤F(ω，(ξ0(ω)，η0(ω)))，g(ω，η0(ω))≥F(ω，(η0(ω)，ξ0(ω)))，即g(ω，ξ0(ω))≤g(ω，ξ1(ω))，g(ω，η0(ω))≥g(ω，η1(ω))，從而當n=0時，結論成立.假設對任意的n≥0，結論成立，即

g(ω，ξn(ω))≤g(ω，ξn+1(ω))，g(ω，ηn(ω))≥g(ω，ηn+1(ω)).

下證對n+1時結論成立.事實上，由F對于第一個變量具有單調g-非減性，

F(ω，(ξn(ω)，ηn(ω)))≤F(ω，(ξn+1(ω)，ηn(ω)))，

F(ω，(ηn+1(ω)，ξn(ω)))≤F(ω，(ηn(ω)，ξn(ω))).

(3)

由F對于第二個變量具有單調g-非增性，

F(ω，(ξn+1(ω)，ηn+1(ω)))≥F(ω，(ξn+1(ω)，ηn(ω)))，

F(ω，(ηn+1(ω)，ξn(ω)))≥F(ω，(ηn+1(ω)，ξn+1(ω))).

(4)

由(3)—(4)式及不等式的傳遞性有

F(ω，(ξn+1(ω)，ηn+1(ω)))≥F(ω，(ξn(ω)，ηn(ω)))，

F(ω，(ηn(ω)，ξn(ω)))≥F(ω，(ηn+1(ω)，ξn+1(ω)))，

從而g(ω，ξn+1(ω))≤g(ω，ξn+2(ω))，g(ω，ηn+1(ω))≥g(ω，ηn+2(ω))，即結論在n+1時成立.

定義δn=d(g(ω，ξn(ω))，g(ω，ξn+1))+d(g(ω，ηn(ω))，g(ω，ηn+1(ω))).注意到

d(g(ω，ξn(ω))，g(ω，ξn+1))=

d(F(ω，(ξn-1(ω)，ηn-1(ω)))，F(ω，(ξn(ω)，ηn(ω))))≤

αd(g(ω，ξn-1(ω))，g(ω，ξn))+βd(g(ω，ηn-1(ω))，g(ω，ηn(ω)))，

(5)

d(g(ω，ηn(ω))，g(ω，ηn+1))=

d(F(ω，(ηn-1(ω)，ξn-1(ω)))，F(ω，(ηn(ω)，ξn(ω))))≤

αd(g(ω，ηn-1(ω))，g(ω，ηn))+βd(g(ω，ξn-1(ω))，g(ω，ξn(ω)))，

(6)

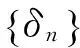
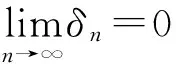
現在證明{g(ω，ξn(ω))}和{g(ω，ηn(ω))}是柯西列，用反證法.若{g(ω，ξn(ω))}和{g(ω，ηn(ω))}至少有一個不是柯西列，則存在ε>0，和兩個正整數序列{m(k)}，{l(k)}，m(k)>l(k)>k，滿足：

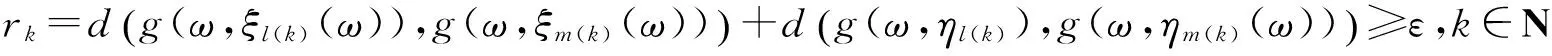
(7)

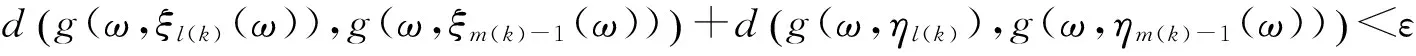
(8)

實際上可以選擇使得(7)式成立的最小m(k)，此時必然可以使得(8)式成立.由(7)—(8)式與三角不等式有

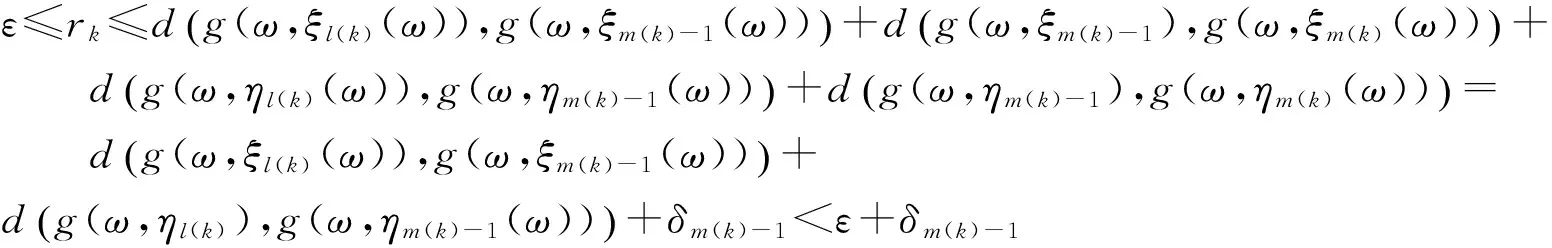
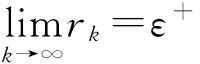
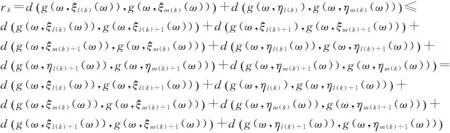
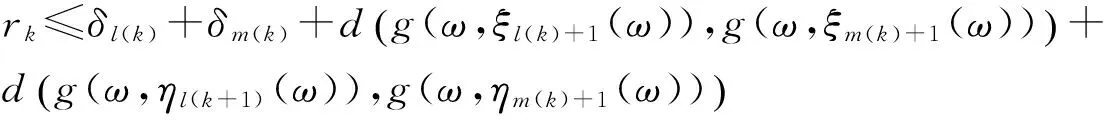
(9)

而

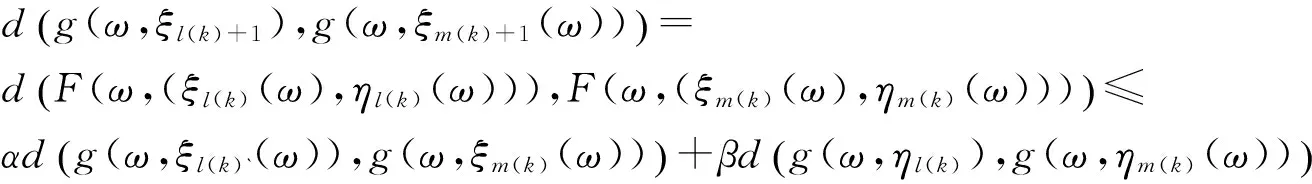
(10)

(11)

(10)和(11)式相加得

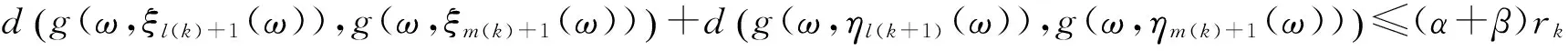
將之代入(9)式得rk≤δl(k)+δm(k)+(α+β)rk，令k→∞有ε≤0+0+(α+β)ε<ε，矛盾.故假設不成立，{g(ω，ξn(ω))}和{g(ω，ηn(ω))}是柯西列.

由g(X×X)=X的完備性，存在θ0，ξ0∈Θ，使得

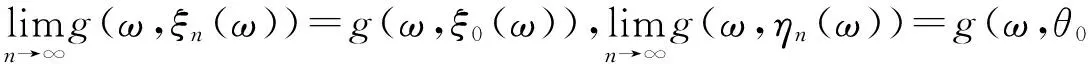
由g(ω，ξ0(ω))，g(ω，θ0(ω))是可測的，故可定義ξ(ω)=g(ω，ξ0(ω))，θ(ω)=g(ω，θ0(ω))，即有

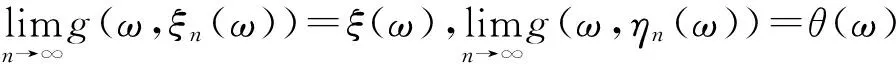
(12)

由(12)及g的連續性，

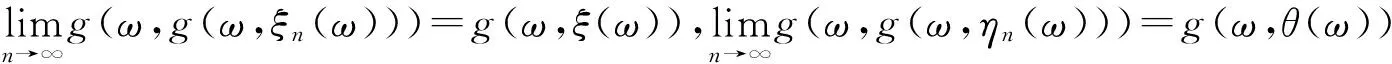
(13)

由F和g的可交換性有

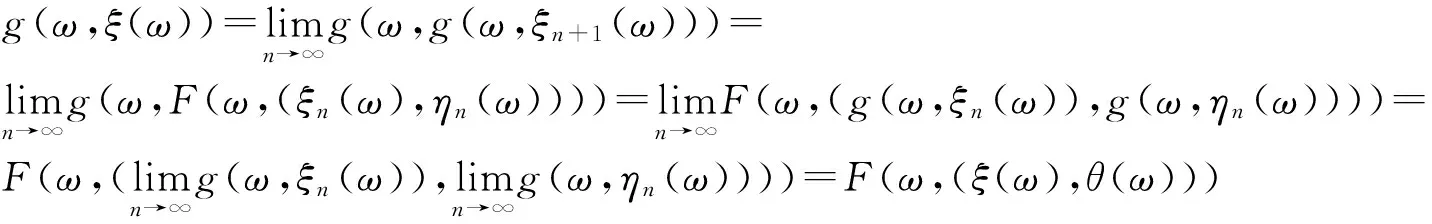
(14)

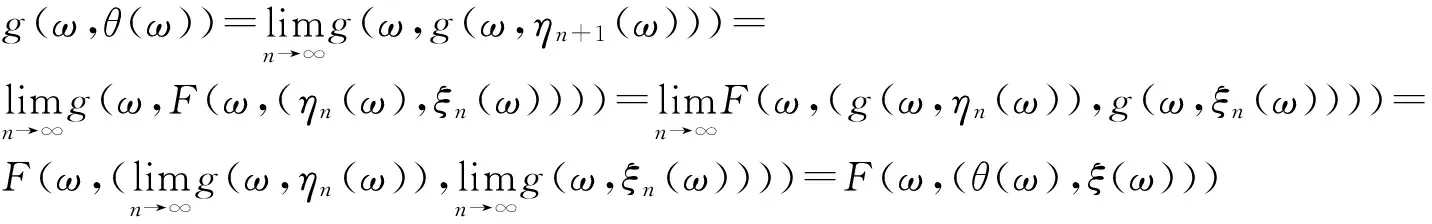
(15)

故F(ω×(ξ(ω)，θ(ω)))=g(ω，ξ(ω))，F(ω×(θ(ω)，ξ(ω)))=g(ω，θ(ω))，即(ξ(ω)，θ(ω))∈X×X是F和g的耦合隨機重合點.

以下說明在(A6)的條件下，結論也成立.事實上，假設(A6)成立，由(A2)可知{g(ω，ξn(ω))}是非減的，且當g(ω，ξn(ω))→g(ω，ξ(ω))時，g(ω，ξn(ω))≤g(ω，ξ(ω))，n∈N.同時，由(A2)可知{g(ω，ηn(ω))}是非增的，且當g(ω，ηn(ω))→g(ω，θ(ω))時，有g(ω，ηn(ω))≥g(ω，θ(ω))，n∈N.由三角不等式，

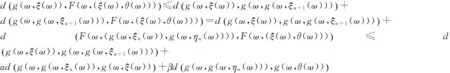
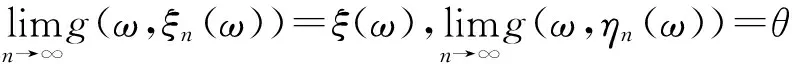
類似可證F(ω×(θ(ω)，ξ(ω)))=g(ω，θ(ω))，故(ξ(ω)，θ(ω))∈X×X是F和g耦合隨機重合點.

定理2 設(X，≤)是一個偏序集，(X，d)是完備可分的度量空間，(Ω，Σ)是一個可測空間，F:Ω×(X×X)→X和g:Ω×X→X為混合單調算子.假設(A1)—(A6)成立，且對k∈(0，1)及所有滿足x≤u，y≥v的x，y，u，v∈X，有

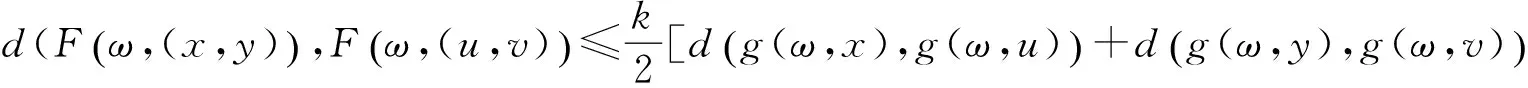
如果存在可測映射ξ0，η0∈X，使得ξ0(ω)≤F(ω，(ξ0(ω)，η0(ω)))，F(ω×(η0(ω)，ξ0(ω)))≤η0(ω)，則也存在可測映射ξ，θ:Ω→X，使得F(ω×(ξ(ω)，θ(ω)))=ξ(ω)，F(ω×(θ(ω)，ξ(ω)))=θ(ω)，?ω∈Ω.即F和g存在耦合隨機不動點點.

[1] GUO D J，LAKSHMIKANTHAM V. Nonlinear problems in abstract cone[M].New York：Academic Press，1988：267-275.

[2] GUO D J，LAKSHMIKANTHAM V. Coupled fixed points of nonlinear operators with application[J]. Nonlinear Analysis，1987，11(5):623-637.

[3] JIANG B H，XU S Y.Couple coincidence points for mixed monotone random operators in partially ordered metric space[J/OL].Abstract and Applied Analysis，2014[2014-12-12].http://dx.doi.org/10.1155/2014/484857.

[4] 王梓坤.隨機泛函分析引論[J].數學進展，1962，5(1)：45-71.

[5] 郭大鈞.非線性泛函分析[M].濟南:山東科技出版社，1985:235-241.

[6] 梁瑛，吳宏鍔.隨機混合算子的耦合不動點定理[J].綿陽師范學院學報，2009，28(2):24-27.

[7] 李國禎，朱傳喜.關于混合單調算子的耦合不動點定理[J].工程數學學報，1993，10(1):9-16.

[8] 許紹元.混合單調算子不動點存在唯一性定理及其應用[J].吉首大學學報(自然科學版)，2011，32(1)：11-13.

[9] 盛梅波.關于混合單調算子的新的不動點定理及應用[J].華東交通大學學報(理科版)，2003(5)：118-200.

(責任編輯：李亞軍)

Couple coincidence points for mixed monotone random operators in partially ordered metric space

LI Cheng-geng，XU Shao-yuan，LIU Bo

(Department of Mathematics and Applied Mathematics，Hanshan Normal University，Chaozhou 521041，China)

Random mixed monotone operators in partially ordered metric spaces are considered. The results improve the problem of coincidence points for general monotone operators to mixed monotone random operators.

partially ordered;coupled coincidence points;mixed monotone operators； random operator

1000-1832(2016)04-0015-04

10.16163/j.cnki.22-1123/n.2016.04.004

2014-12-12

國家自然科學基金資助項目(10961003).

李承耕(1969—)，男，碩士，講師，主要從事統計與非線性泛函研究；許紹元(1964—)，男，博士，教授，主要從事分行幾何與非線性泛函研究；劉波(1977—)，男，碩士，講師，主要從事統計與非線性泛函研究.

O 177.91 [學科代碼] 110·67

A