航空重力數據向下延拓的迭代Tikhonov正則化法

馮淑萍，高延民

（1.西安測繪總站，陜西 西安 710054）

航空重力數據向下延拓的迭代Tikhonov正則化法

馮淑萍1，高延民1

（1.西安測繪總站，陜西 西安 710054）

根據觀測面和延拓面測量數據的Poisson積分平面近似關系，結合快速傅立葉變換算法，將向下延拓轉換到頻率域進行計算，并采用迭代Tikhonov正則化方法，克服計算的不穩定性，提高計算結果的精度，實現了航空重力測量數據的向下延拓。最后采用模擬航空重力測量數據驗證了該算法的有效性，取得了較好的延拓結果。

航空重力；向下延拓；正則化參數；迭代Tikhonov正則化法；快速傅立葉變換

在實際的工作中，航空重力測量常常是在起伏的航線上進行的，然而重力資料的定量解釋方法要求測量數據分布在一個平面上，因此，需要將實測資料向下延拓到一個平面上。而向下延拓是一個典型的不適定問題[1-2]，主要表現為計算的不穩定性。隨著向下延拓深度的增大，會對重力測量數據中的高頻干擾信號起顯著的放大作用，從而不能分辨有效信號。為了解決這個問題，本文采用迭代Tikhonov正則化方法來實現航空重力測量數據的向下延拓。

1 向下延拓的基礎模型

航空重力測量數據向下延拓的基本原理如圖1所示。

圖1 向下延拓示意圖

圖中，Δgh（ξ，η）表示觀測面上的航空重力測量數據；Δg0（x，y）表示延拓面上的航空重力測量數據。計算觀測面以下至場源以上z=0這個平面的航空重力測量數據稱為航空重力測量數據的向下延拓。

根據航空重力測量數據向上延拓公式，可得觀測面航空重力測量數據與延拓面重力數據之間的近似關系公式[3-6]：

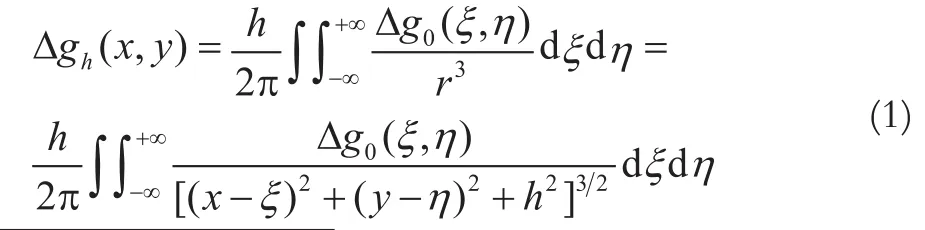
式中，h是向下延拓深度；r是延拓面上點（x，y，0）與觀測面上點（ξ，η，h）之間的距離。式（1）是第一類Fredholm積分方程，具有實對稱核，且可以表示為二維卷積：

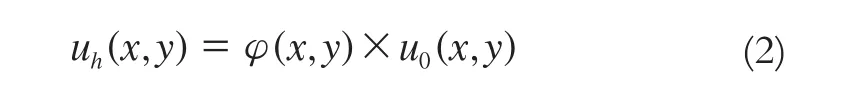
其中：

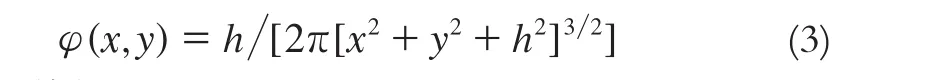
將式（2）轉換到譜域里計算，其譜表達式為：

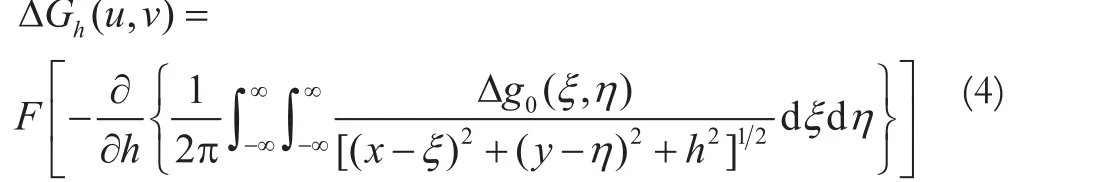
因為：

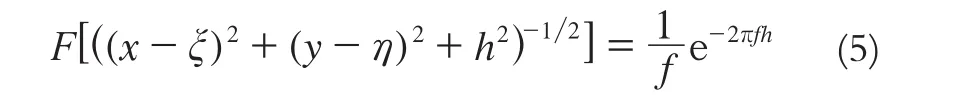
其中，f=（u2+v2）1/2；u、v分別表示空域變量x、y對應的頻域變量。將式（5）代入式（4），可以得到：

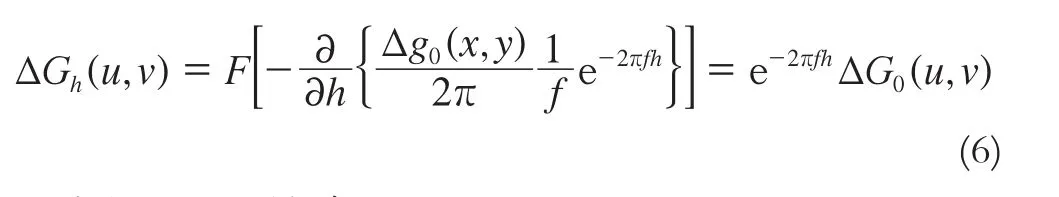
通過變換可以得到：

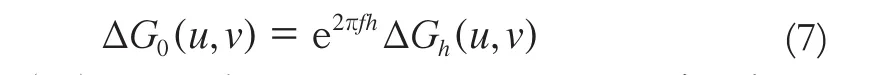
對式（7）兩端進行Fourier逆變換，得到延拓面重力數據：

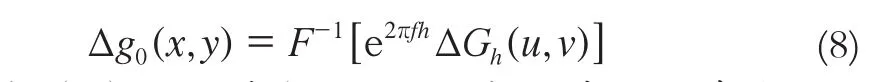
從式（8）可以看出，向下延拓的基礎數學模型原理比較簡單，但是由于其向下延拓算子 的不穩定性對航空重力測量數據中的高頻噪聲有著顯著的放大作用，在延拓深度較大時會導致延拓結果精度不高，要解決這種不適定問題，可引入正則化因子。因此，本文研究了迭代Tikhonov正則化法數學模型。

2 迭代Tikhonov正則化方法

式（2）可以修改為：

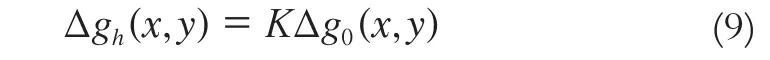
式中，K表示第一類Fredholm積分算子。對于求解不適定問題采用Tikhonov正則化是一個常用的方法，它指的是求解一個極小化的正則化泛函，即

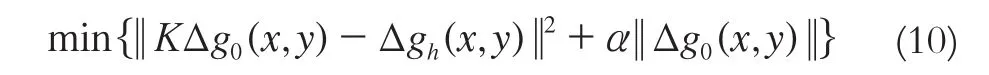
式中，α為正則化參數，用于平衡不穩定性和光滑性。上式等價于如下的Euler方程：

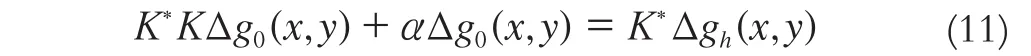
K*為算子K的伴隨算子，由于航空重力測量數據向下延拓的Fredholm算子K為對稱的線性緊算子，有：

因此，式（11）可以表示為：

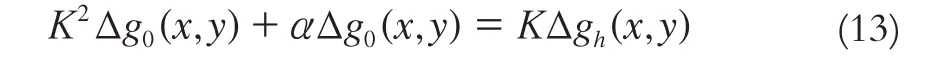
即

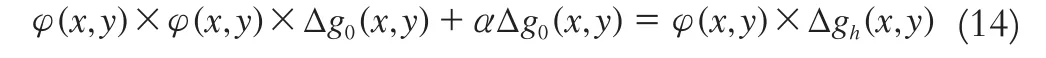
對式（14）兩邊同時作傅立葉變換，得到：

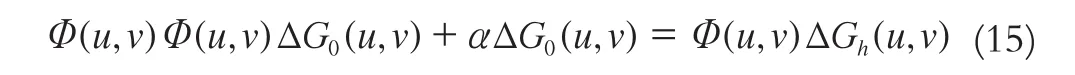
經過調整，可以得到：

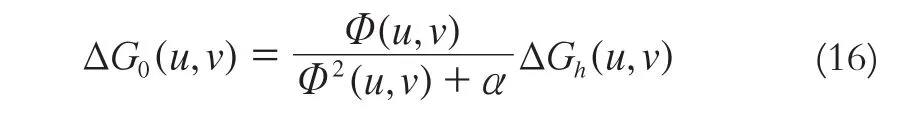
考慮到式（5）、（6），式（16）可以變形為：

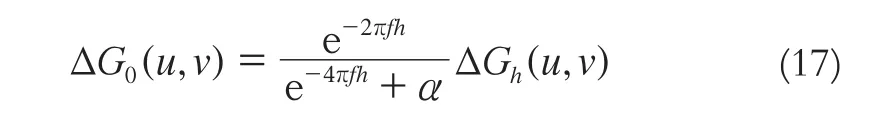
在式（17）兩端進行Fourier逆變換，即可得到航空重力測量數據向下延拓的Tikhonov正則化法公式為：

由于Tikhonov正則化的飽和效應，使得正則化解與準確解的誤差估計不能達到階數最優，迭代的Tikhonov正則化對此進行了改進，其迭代形式如下：

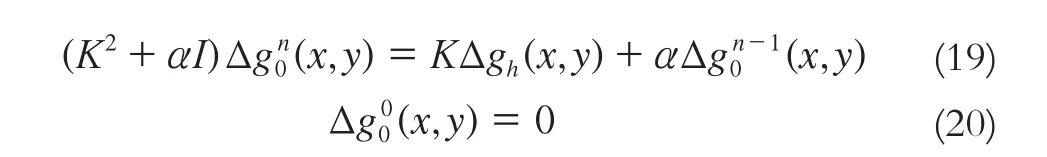
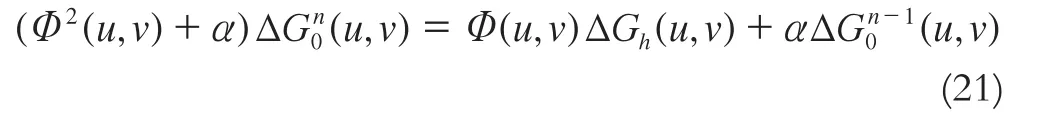
將上式變形為：

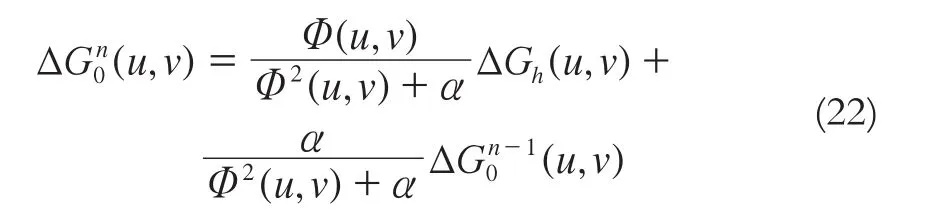
根據數學歸納法，式（22）又可以寫為：

根據式（20），式（23）可以改化為：

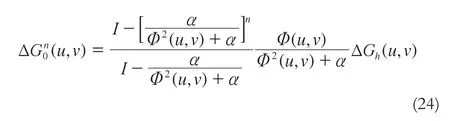
再根據式（5）、（6），經過化簡，可以得到：

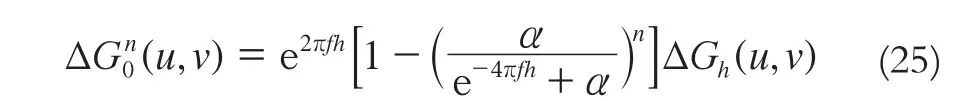
在式（24）兩端進行Fourier逆變換，可得到航空重力測量數據向下延拓的迭代Tikhonov正則化法公式為[7～13]：

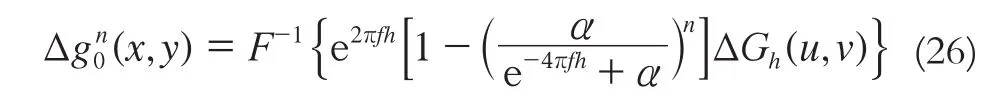
3 數值實驗與結果分析

3.1 航空重力測量數據仿真

采用2 160階的EGM2008地球重力場模型，對中國某地區的航空重力測量數據和地面重力數據進行仿真。將航空重力測量飛機的飛行高度設為3 000 m，分辨率設為5'×5'。圖2和圖3分別表示觀測面理論航空重力測量數據和延拓面理論重力數據。為了驗證本課題向下延拓算法的有效性，在觀測面理論航空重力測量數據中加入均值為0、標準差為3 mGal的高斯白噪聲，其等值線圖如圖4所示。

3.2 迭代Tikhonov正則化法實驗結果

在對迭代Tikhonov正則化方法的延拓精度進行測試時，首先需要對延拓誤差與正則化因子的關系進行驗證。表1表示迭代Tikhonov正則化法在取得最小延拓誤差時對應的正則化因子和迭代次數。因此，表1的統計結果進一步證實了所得出的結論。

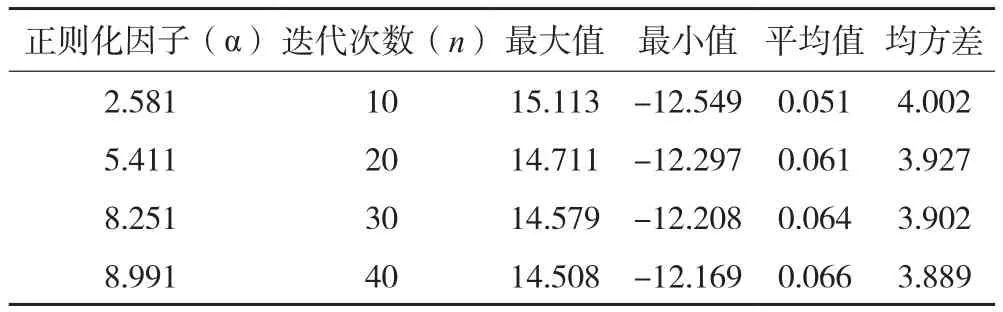
表1 最小延拓誤差對應的正則化因子和迭代次數/mGal

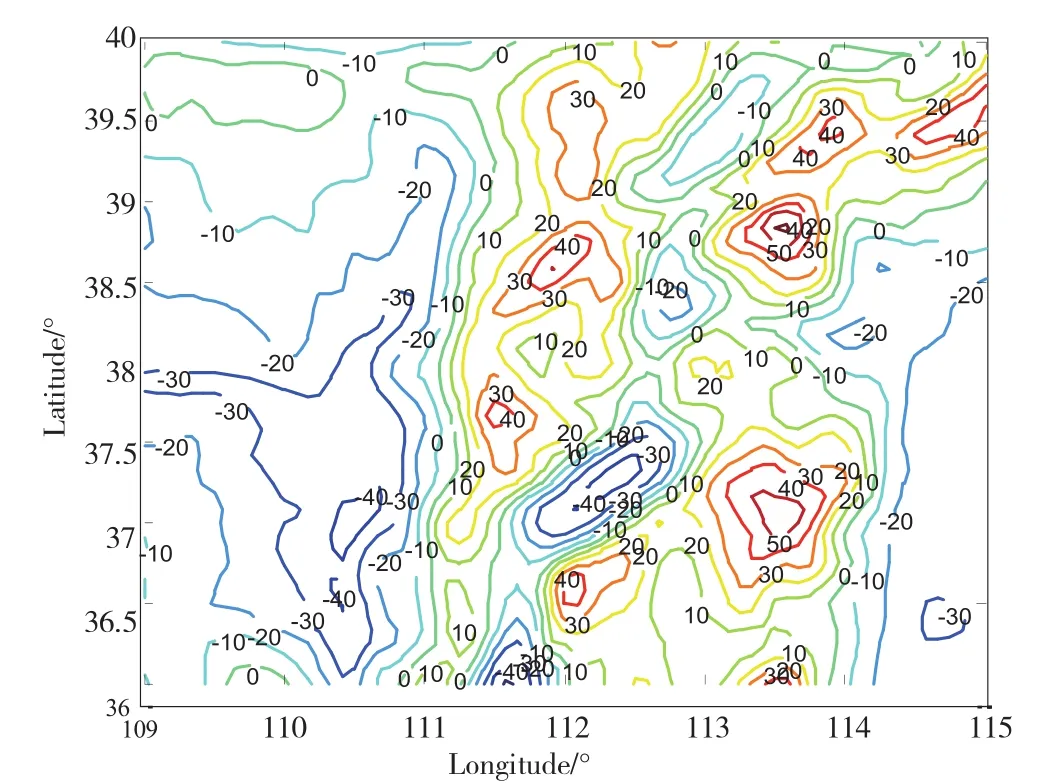
圖2 觀測面理論航空重力測量數據等值線/mGal

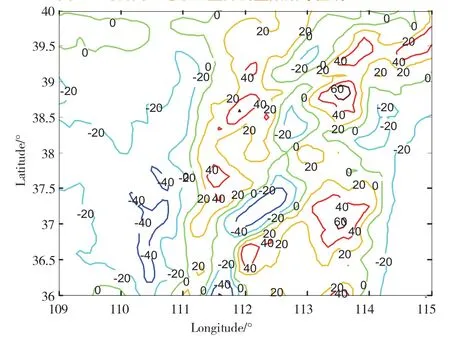
圖3 延拓面理論重力數據等值線/mGal

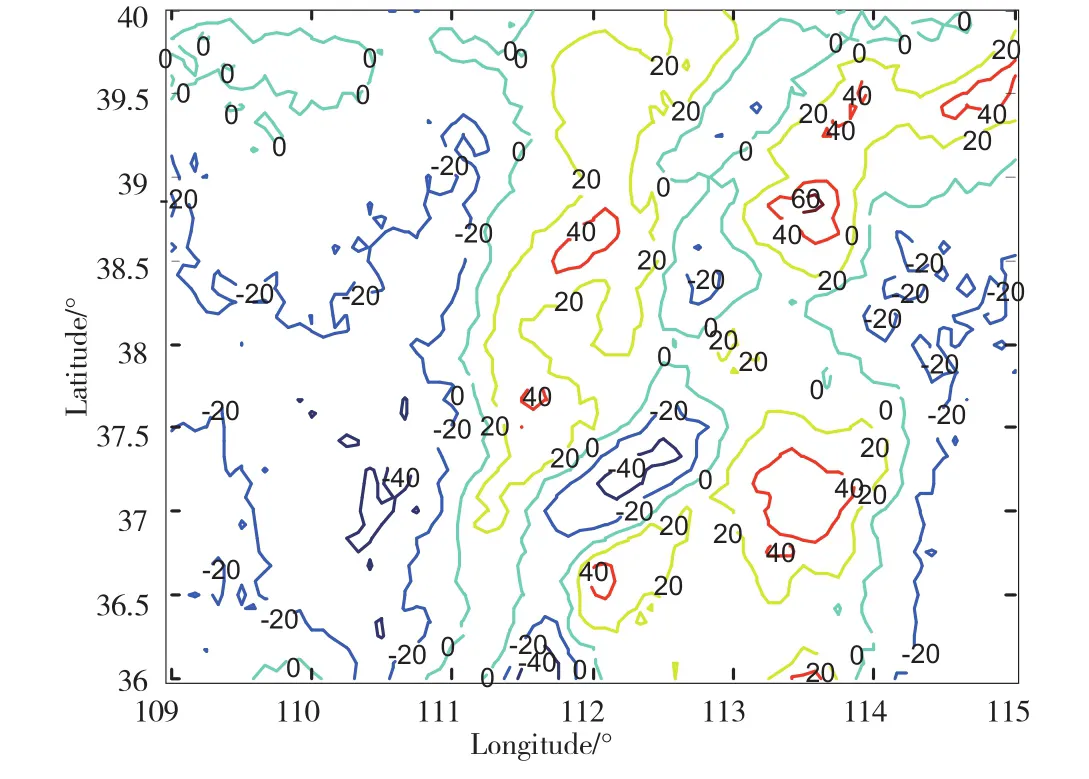
圖4 含有高斯白噪聲的觀測面航空重力測量數據等值線/mGal

圖5給出了迭代Tikhonov正則化法在取得最小延拓誤差，即α=8.251時對應的延拓結果的等值線圖。

從圖3和圖5的比較來看，迭代Tikhonov正則化方法延拓結果對延拓面上理論重力數據的逼近效果較好。

確定合適的正則化參數是迭代Tikhonov正則化法獲取最優解的關鍵，如果α遠大于1，將導致逼近問題對原問題過于光滑，使計算結果與原問題的解相差甚遠；相反，如果α遠小于1，則逼近問題未能很好地改良算子的譜，正則化迭代法的效果不明顯。

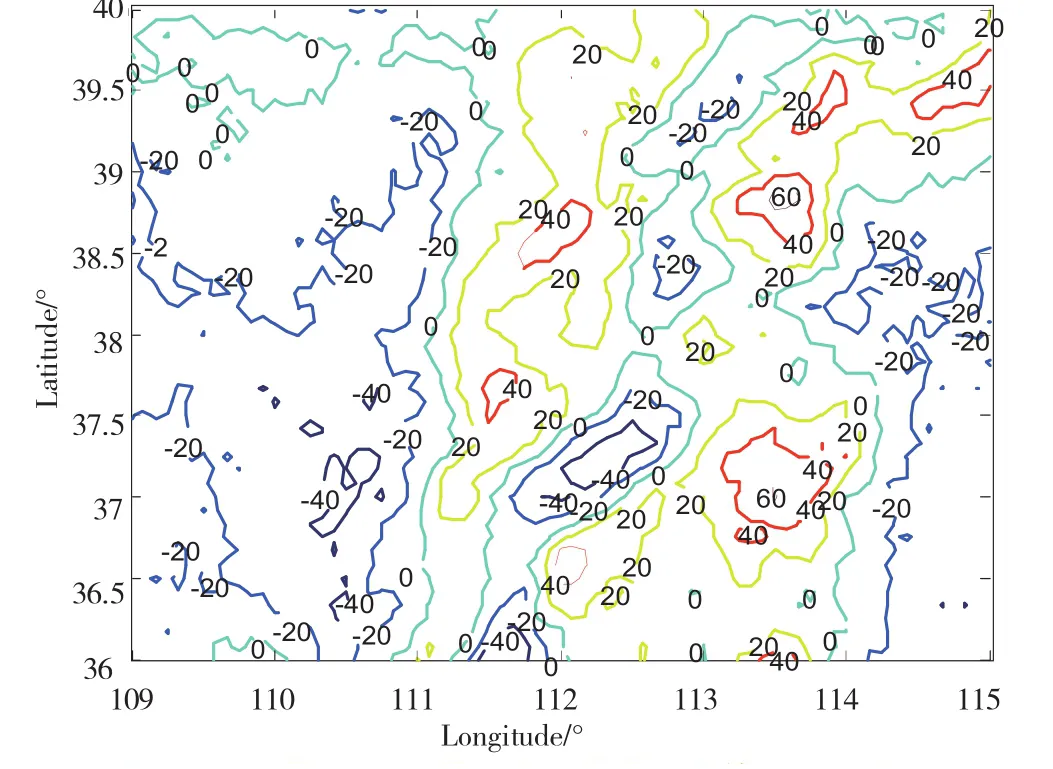
圖5 迭代Tikhonov正則化法延拓結果等值線/mGal

[1] 欒文貴.場位解析延拓的穩定化算法[J].地球物理學報,1983,26(3):263-274

[2] 梁錦文.位場向下延拓的正則化方法[J].地球物理學報,1989,32(5):600-608

[3] 王興濤,夏哲仁,石磐,等.航空重力測量數據向下延拓方法比較[J].地球物理學報,2004,47(6):1 017-1 022

[4] 羅志才,寧津生,晁定波.衛星重力梯度向下延拓的譜方法[J].測繪學報,1997,26(2):168-175

[5] 孫中苗.航空重力測量理論方法及應用研究[D].鄭州:信息工程大學,2004

[6] 劉曉剛,李珊珊,吳星.衛星重力梯度數據的向下延拓[J].大地測量與地球動力學,2011,31(1):132-137

[7] TIKHONOV A N, ARSENIN V Y. Solution of Certain Integral Equations of the First Kind[J]. J Assoc Comput Mach, 1962 (9):84-97

[8] 成怡,郝燕玲,劉繁明.航空重力測量數據向下延拓及其影響因素分析[J].系統仿真學報,2008,20(8):2 190-2 194

[9] 郝燕玲,成怡,孫楓,等.Tikhonov正則化向下延拓算法仿真實驗研究[J].儀器儀表學報,2008,29(3):605-609

[10] 鄧凱亮,暴景陽,黃謨濤,等.航空重力數據向下延拓的Tikhonov正則化法仿真研究[J].武漢大學學報(信息科學版),2010,35(12):1 414-1 417

[11] 曾小牛,李夕海,韓紹卿,等.位場向下延拓三種迭代方法之比較[J].地球物理學進展,2011,26(3): 908-915

[12] 鄧凱亮,黃謨濤,暴景陽,等.向下延拓航空重力數據的Tikhonov雙參數正則化法[J].測繪學報,2011,40(6):690-696

[13] 蔣濤,李建成,王正濤,等.航空重力向下延拓病態問題的求解[J].測繪學報,2011,40(6):112-122

P223

B

1672-4623（2016）10-0053-03

10.3969/j.issn.1672-4623.2016.10.015

馮淑萍，工程師，主要從事航空重力研究。

2015-07-13。

項目來源：國家自然科學基金資助項目（41304022）；國家重點基礎研究發展計劃資助項目（61322201，2013CB733303）；高分專項青年創新基金資助項目（GFZX04060103-5-12）。