基于車橋耦合的高架槽形梁結構噪聲影響分析

曾 峰，劉林芽，吳宇鵬，宋 瑞

（華東交通大學 鐵路環境振動與噪聲教育部工程研究中心,南昌 330013）

基于車橋耦合的高架槽形梁結構噪聲影響分析

曾 峰，劉林芽，吳宇鵬，宋 瑞

（華東交通大學 鐵路環境振動與噪聲教育部工程研究中心,南昌 330013）

為了探討列車通過軌道交通高架槽形梁時誘發的結構噪聲，以某擬建30 m軌道交通槽形梁為研究對象，建立車橋耦合系統振動分析模型以及槽形梁結構聲輻射有限元/邊界元模型。采用多體動力學軟件Simpack建立列車的空間動力學模型，采用有限元軟件Ansys建立槽形梁有限元模型，基于Simpack和Ansys相結合的聯合仿真方法，獲取輪軌激振力。在計算列車荷載作用下槽形梁結構振動響應的基礎上，采用有限元-間接邊界元耦合聲學分析法，探討底板厚度以及腹板高度對槽形梁結構噪聲的影響。研究結果表明：底板厚度的增加可以降低槽形梁梁體正下方的結構噪聲，但并非越厚越好，底板厚度對結構遠聲場有一定程度的影響，但降噪效果不明顯；腹板高度的變化使槽形梁結構噪聲輻射衰減方向有所改變，橋梁腹板兩側噪聲輻射衰減速度較快；橋梁底板正上方的結構輻射噪聲最強區域有縮小趨勢；分析結果可為軌道交通槽形梁結構減振降噪優化設計提供一定的理論參考依據。

振動與波；耦合振動；聯合仿真；結構噪聲；有限元；間接邊界元

大力發展軌道交通是解決城市交通擁擠最有效的途徑之一[1]，但是高架結構的振動與噪聲影響已成為制約城市軌道交通發展的重要因素[2]。因此，研究軌道交通高架橋梁結構輻射噪聲的影響，對于選擇合理的減振降噪措施、優化橋梁結構設計、促進交通行業的發展具有重要意義。

軌道交通高架橋梁在列車荷載的作用下誘發振動，并向周圍環境輻射噪聲，其中0～100 Hz頻段的噪聲屬于低頻噪聲[3-4]。而低頻噪聲具有繞射能力強、衰減較慢等特點，并且該頻段噪聲對人體有長期性危害，因此有必要針對軌道交通槽形梁的結構噪聲展開研究[5]。

影響軌道交通槽形梁結構輻射噪聲的因素很多，橋梁結構形式、結構參數、結構剛度等均可對橋梁結構的聲輻射特性產生影響。張迅、李小珍等通過對簡支梁結構噪聲的理論分析和試驗測試，研究發現板厚是影響結構噪聲的重要參數[6]。韓江龍、吳定俊等采用模態疊加法分析了橋梁的結構噪聲和不同構件的聲壓貢獻量，研究發現增加底板的厚度可以降低梁底的結構噪聲[7]。但方小華，古愛軍等研究發現：橋梁底板厚度的變化對橋梁各個板件的振動、噪聲無明顯影響，腹板厚度的變化對橋梁的振動和噪聲影響較小[8]。Bewes通過對不同橋梁結構進行研究，發現橋梁某些結構組件厚度的增加，可以降低這一組件的結構噪聲，但同時會增加其他組件的結構噪聲[9]。因此，板厚對槽形梁結構噪聲的影響亟待進一步分析研究。

工程實踐中，高架槽形梁因其自身構型的特殊性，兩側的腹板具有阻隔輪軌噪聲的功能，同時大量減少了高架軌道聲屏障的使用[10]。但腹板結構高度對綜合輻射聲場的影響少見文獻報道。

文中以某擬建30 m的簡支槽形梁為研究對象，基于Simpack和Ansys相結合的聯合仿真方法，建立車橋耦合系統振動分析模型以及槽形梁結構聲輻射有限元/邊界元模型，獲取輪軌激振力，在計算列車荷載作用下槽形梁結構振動響應的基礎上，采用有限元-間接邊界元耦合聲學分析法，探討了底板厚度以及腹板高度對槽形梁結構噪聲的影響。

1 軌道交通槽形梁振動聲輻射計算模型

1.1 軌道交通高架槽形梁橋模型

某軌道交通集團擬建高架段為平坡線路，擬采用雙線分離式結構，橋的結構類型為槽形梁，橋墩為T型墩，如圖1所示。

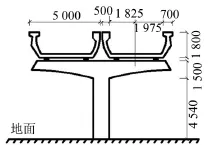
圖1 擬建高架槽形梁橋梁截面（單位/mm）

槽形梁的標準跨徑為29.94 m，梁寬為5 m，高為1.8 m，底板厚度為0.28 m，腹板厚度為0.24 m，支座設在距梁端0.57 m處。

1.2 軌道交通槽形梁有限元模型

基于有限元理論，建立軌道交通槽形梁模型。在分析模型中，所有材料均處于線彈性階段，將鋼軌視為Euler梁，用梁單元模擬；槽形梁梁體、軌道板、CA砂漿層均用實體單元模擬，為避免病態網格的出現，采用體掃掠法將其劃分為大小合適的六面體單元；連接鋼軌與軌道板的扣件系統采用間距為0.625 m的離散彈簧阻尼單元模擬，主要結構參數見表1。

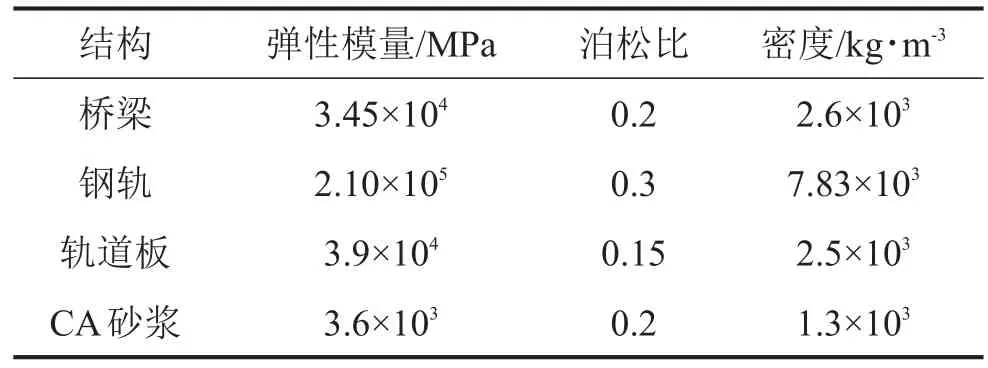
表1 槽形梁模型主要結構參數表

槽形梁的截面形式參照某擬建軌道交通選用的簡支槽形梁設計圖紙，梁體腹板一側為圓弧結構、另一側采用折腹線式直線的不對稱結構，有限元模型如圖2所示。

圖2 軌道交通槽形梁有限元模型

各項參數經過多次調試，能滿足GB50157-2013地鐵設計規范的要求[11]。

1.3 軌道交通槽形梁邊界元模型

基于流體介質的守恒原理和關于聲波動的一些基本假設，采用變量分離法，由三維波動方程可知槽形梁聲輻射的Helmholtz方程表達式如下

式中Δ2為拉普拉斯算子；k=ω/c為聲波波數；c為空氣介質中的聲速；ω為圓頻率；p為聲場任意點的聲壓。

槽形梁結構振動體表面的運動可認為是小振幅的，其屬于不滲透邊界，邊界條件為

式中vn表示表面法向振速；n表示橋梁結構振動體表的外法線；ρ表示流體密度；i表示虛數單位。

基于邊界條件，利用加權殘值法，可得到式（1）的基本解，為

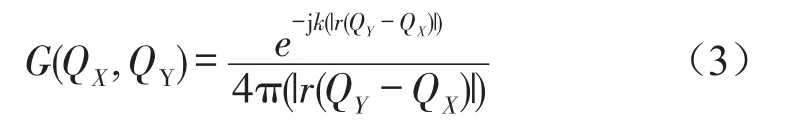
式中QX表示結構表面上任意點，QY表示聲場中的任意點。

確定邊界元兩側的聲壓差和聲壓梯度差，然后將Helmholtz積分方程應用于邊界表面兩側，即可獲得聲場中任意場點的聲壓

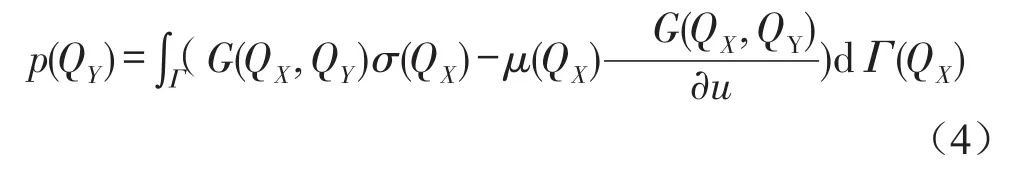
式中σ（QX）、μ（QX）分別表示QX點橋梁結構表面兩側振速差和聲壓差。Γ表示邊界表面。

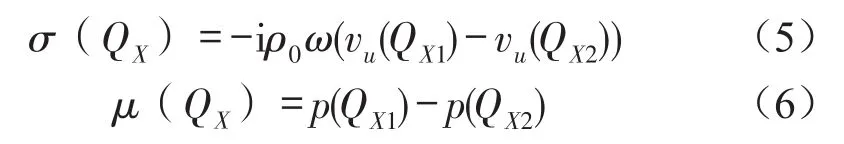
式中ρ0為空氣密度；vu(QX1)、vu(QX2)分別表示橋梁結構表面上任意點QX兩側的法向振速；p(QX1)、p(QX2)分別表示橋梁結構表面上任意點QX兩側的聲壓。

利用邊界單元離散化橋梁結構表面，可得到橋梁結構表面邊界上每個節點的兩側振速差和聲壓差為

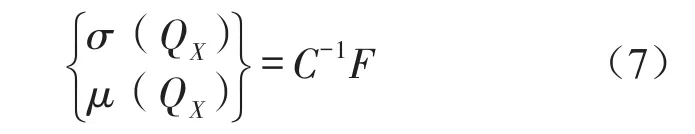
式中C表示對稱的復數滿秩矩陣；F表示荷載激勵向量。

由式（7）可得槽形梁結構聲場外任意點QY處的聲壓

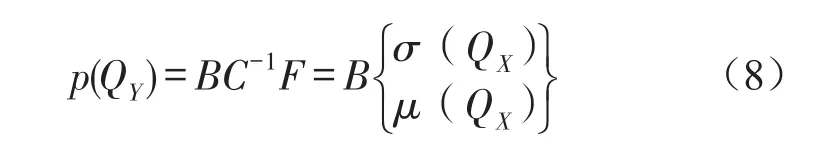
式中B表示復數滿秩矩陣，與結構的表面形式等有關。

基于有限元-間接邊界元耦合聲學理論，建立了高架槽形梁邊界元模型。在建立聲學邊界元模型時，考慮最大單元的邊長要小于計算頻率最短波長的1/6，即最大單元的邊長要滿足如下表達式

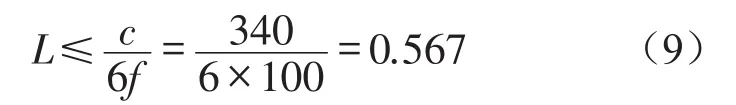
式中c表示為聲速，取340 m/s。采用間接邊界元法計算橋梁結構振動聲輻射情況時，槽形梁邊界元網格劃分最大單元尺寸為0.312 5，滿足式（9）。槽形梁邊界元網格如圖3所示。

圖3 軌道交通槽形梁邊界元模型及場點網格

1.4 車橋耦合模型

為了避免車橋耦合振動分析交叉迭代計算量較大的弊端，基于多體動力學理論，建立精細化車橋耦合的空間動力學分析模型。地鐵列車模型的結構參數及動力學參數參照實際地鐵B型車選取，在作一些簡化的基礎上，通過Simpack建立。其中每一節地鐵車輛動力學分析模型可以認為由1個車體、2個轉向架（含4個輪對）等剛體組成，每一節剛體車輛考慮了伸縮、橫擺、浮沉、點頭、測滾、搖頭6個自由度，每一節車輛共考慮34個自由度。輪對和轉向架以及轉向架和車體之間分別通過一系、二系彈簧連接；輪軌接觸采用單點非線性彈性接觸；軌道不平順選用美國6級不平順譜。列車基本參數見表2。

表2 列車基本參數

將基于有限元軟件Ansys建立的槽形梁有限元模型作為柔性體導入多體動力學軟件Simpack中，同時，導入槽形梁模態分析和子結構分析的結果文件。利用Simpack中柔性軌道模塊，實現列車模型和橋梁模型的共同求解。其中，將列車模型和槽形梁有限元模型分別作為兩個系統，分別求解輪流迭代。車橋耦合模型之間通過輪軌接觸離散點實現位移、速度、作用力的交換。為了控制車輛系統和橋梁系統所有自由度的計算結果相對于前一迭代步的誤差都不超過系統迭代控制誤差精度的要求，文中控制精度取10-4。車橋耦合模型如圖4所示。

圖4 車橋耦合模型

2 輪軌激振力的獲取和加載

基于車橋耦合模型，采用聯合仿真法,模擬輪軌之間的相互作用力。采用地鐵車輛6節編組模擬加載，計算速度為80 km/h。最終得到輪軌垂向作用力。

將列車實際運行過程簡化為一系列隨時間移動的集中力荷載，采用節點加載方式分析高架槽形梁的結構噪聲輻射特性，每節車輛按輪對左右對稱分布共8個集中力荷載，加載時間步長為0.005 s，加載方式如圖5所示。

圖5 輪軌激振力加載方式

3 結構噪聲的影響參數分析

3.1 軌道交通槽形梁原模型聲輻射分析

將基于車橋耦合模型計算出來的輪軌激振力加載到軌道-槽形梁有限元模型上，進行軌道交通槽形梁的瞬態動力響應分析，再以軌道交通槽形梁動力響應結果作為邊界條件，采用聲學間接邊界元法進行軌道交通槽形梁結構噪聲預測分析。

為了研究距橋體中心線水平向不同距離處槽形梁的聲場分布規律，沿水平方向分別選取5個場點進行分析。圖6為高架槽形梁聲場輸出場點分布圖，場點1至場點5距地面2 m，距線路中心線的水平距離分別為0 m、5 m、10 m、20 m、25 m。

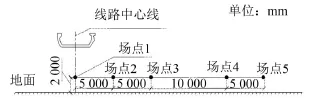
圖6 高架槽形梁聲場輸出場點分布圖

由圖7槽形梁場點線性聲壓級1/3倍頻圖可知，軌道交通槽形梁結構噪聲輻射的優勢頻段基本處在20 Hz～80 Hz，峰值頻率都出現在31.5 Hz和63 Hz附近，這主要源于橋梁振動加速度響應在31.5 Hz附近有一個峰值，而對于最大峰值頻率63 Hz，通過考察槽形梁的模態特征，發現在中心頻率63Hz附近對應有一個振動模態，固在63 Hz處出現最大峰值頻率。這與文獻[7]中實測峰值頻段具有很好的一致性。

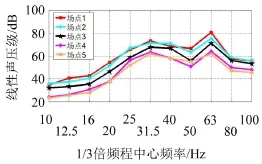
圖7 槽形梁場點線性聲壓級1/3倍頻程曲線

3.2 底板厚度對結構噪聲的影響分析

以擬建30 m標準跨徑槽形梁為標準模型，通過改變底板厚度或者改變腹板的高度，得到其他模型，結構示意圖如圖8所示。

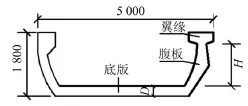
圖8 槽形梁結構截面示意圖（單位/mm）

其中板件厚度和高度滿足《混凝土結構構造手冊》的要求[12]。

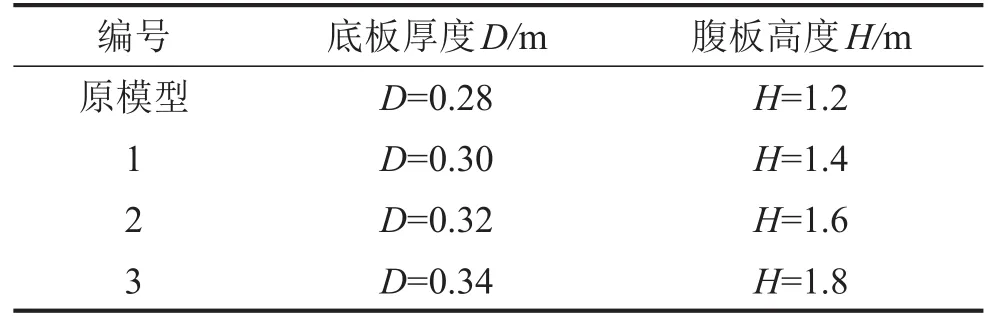
表3 槽形梁模型參數表

鑒于槽形梁結構噪聲主要集中在100 Hz以下，同時，為了避免A計權對低頻噪聲的削弱，因此選取10 Hz～100 Hz頻率范圍內的聲場點處線性聲壓級來分析結構底板厚度對槽形梁輻射噪聲的影響。圖9給出了不同聲學場點10 Hz～100 Hz頻段內線性聲壓級最大值。

由圖9可知，從槽形梁跨中正下方場點1到場點3，槽形梁壁板厚度的變化對梁體結構噪聲的控制有一定效果，隨著底板厚度的增加，結構輻射的噪聲降低，但減少量隨板厚的增加而逐漸減小，這是由于槽形梁底板直接承受列車荷載的作用，其厚度的增加，結構底板的抗彎剛度增大。

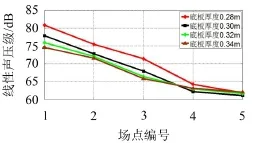
圖9 不同聲學場點線性聲壓級最大值

在距橋梁中心線20 m、25 m處的場點4、場點5，隨著底板厚度的增加，其線性聲壓級最大值降低不明顯，甚至有升高的現象，這是由于隨著底板厚度的增加，其結構質量、輻射面積增大，噪聲的輻射效率同時增大，造成了底板厚度為0.34 m時，出現場點線性聲壓級最大值升高現象，說明通過底板厚度的變化控制槽形梁結構噪聲的措施是適當的。

由圖9可以發現，槽形梁結構噪聲輻射規律較為復雜。同時，為了進一步表征在各個頻段內，槽形梁底板厚度的變化對橋梁結構噪聲輻射的影響，在分析各個場點的1/3倍頻程中心頻率處的最大線性聲壓級基礎上，利用聲壓級累計疊加原理，計算各個場點在10 Hz～100 Hz頻段內的總體線性聲壓級。

由圖10可知，底板厚度的增加對梁體正下方具有較好的降噪效果，但并非越厚越好，底板厚度增大到0.34 m時，出現了聲壓級的增大現象；在距離橋體中心線20 m～25 m的遠聲場，板厚的增加對遠聲場的輻射噪聲降低不明顯。

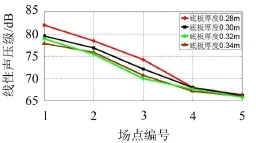
圖10 不同聲學場點總體線性聲壓級

3.3 腹板高度對結構噪聲的影響分析

圖11和圖12分別描述了槽形梁原模型與腹板加高0.6 m兩種工況下跨中截面在63 Hz峰值頻率下的二維聲場分布情況。

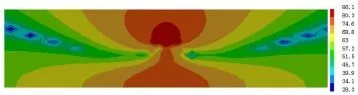
圖11 槽形梁原模型跨中斷面聲壓分布云圖（f=63 Hz，單位/dB）

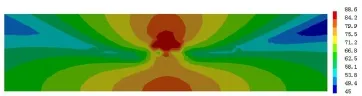
圖12 槽形梁腹板加高0.6 m后跨中斷面聲壓分布云圖（f=63 Hz，單位/dB）

由圖11可知，槽形梁在63 Hz峰值頻率下，底板的振動誘發的噪聲輻射聲壓值較高，聲能量主要集中在底板正上方和正下方區域；槽形梁結構噪聲輻射在橋面板下方衰減較慢；地面附近由于地面對聲波的反射，輻射聲壓出現放大現象；沿著橋梁底板上方45°左右方向衰減較快，圖中表現為云圖顏色變化明顯。

由圖12可知，槽形梁腹板兩側的場點聲壓在63 Hz峰值頻率下結構輻射噪聲衰減較快。與圖11對比發現，隨著槽形梁腹板高度的增加，底板正上方的結構輻射噪聲最強區域有縮小趨勢，體現了槽形梁的遮蔽效應；橋梁腹板兩側噪聲輻射衰減較快；同時，腹板高度的增加使槽形梁綜合聲場結構噪聲輻射衰減方向有所改變，圖中表現為云圖顏色變化明顯。

4 結語

基于Simpack和Ansys相結合的聯合仿真方法，建立車橋耦合系統振動分析模型以及槽形梁結構聲輻射有限元/邊界元模型。在計算列車荷載作用下槽形梁結構振動響應的基礎上，采用有限元-間接邊界元法耦合聲學分析法探討了底板厚度以及腹板高度對槽形梁結構噪聲的影響。通過數值分析得到以下結論：

（1）列車以80 km/h的速度運行在高架橋梁上時，軌道交通槽形梁結構噪聲輻射以20 Hz～80 Hz低頻為主，最大峰值都出現在63 Hz附近。

（2）高架槽形梁底板厚度的增加對梁體正下方具有較好的降噪效果，但并非越厚越好；對結構遠聲場，有一定程度的影響，但降噪效果不明顯。

（3）高架槽形梁腹板高度的增加使槽形梁綜合聲場結構噪聲輻射衰減方向有所改變；橋梁腹板兩側噪聲輻射衰減較快；橋梁底板正上方的結構輻射噪聲最強區域有縮小趨勢。

[1]劉加華，練松良.城市軌道交通振動與噪聲[J].交通運輸工程學報，2002(1)：29-33.

[2]高飛，夏禾，安寧.北京地鐵5號線高架結構的輻射噪聲分析與實驗研究[J].中國鐵道科學，2010(5)：134-139.

[3]劉林芽，許代言.腹板開孔的箱型梁結構噪聲輻射特性分析[J].振動與沖擊，2016，35(15)：204-210.

[4]謝旭，張鶴，山下幹夫，等.橋梁振動輻射低頻噪聲評估方法研究[J].土木工程學報，2008(11)：53-59.

[5]宋曉東，吳定俊，李奇.基于無限元的2.5維方法預測軌道交通混凝土橋梁低頻噪聲[J].振動工程學報，2015，28 (6)：929-936.

[6]張迅，李小珍，劉全民，等.混凝土箱梁的結構噪聲及其影響因素[J].西南交通大學學報，2013，48(3)：409-414.

[7]韓江龍，吳定俊，李奇.板厚和加肋對槽型梁結構噪聲的影響[J].振動工程學報，2012，25(5)：589-594.

[8]方小華，谷愛軍，吳建峰.軌道交通簡支箱梁橋振動傳遞特性分析[J].都市快軌交通，2013，26(3)：84-88.

[9]Bewes O G.The calculation of noise from railway bridges and viaducts[D].University of Southampton,2005.

[10]馬軍旺.城市軌道交通高架線環境景觀適應性探討[J].都市快軌交通，2015，28(6)：132-137.

[11]GB 50157-2013地鐵設計規范[S].北京：中國建設工業出版社，2013.

[12]王文棟.混凝土結構構造手冊（第四版）[M].北京：中國建筑工業出版社，2012.

Analysis for the Structure Noise of Simply Supported Trough Girders Considering Vehicle-bridge Vertical Interaction

ZENG Feng,LIU Lin-ya,WU Yu-peng,SONG Rui
（Engineering Research Center of Railway Environmental Vibration and Noise, Ministry of Education,East China Jiaotong University,Nanchang 330013,China)

The structure noise of simply-supported trough girders in urban rail transit is analyzed.The model of vehiclebridge coupling system for a 30 m reinforced concrete trough girder is built,and the corresponding finite element model and the acoustic boundary element model are established.The train’s spatial dynamics model is established by means of Simpack software,and the finite element model of the girder is established by Ansys software.Based on the combination of Simpack and Ansys codes,the wheel/rail exciting force is obtained.On the basis of calculating the vibration response of the trough girder under the action of train load,and using finite element-indirect boundary element hybrid acoustic analysis method,the influence of the bottom plate thickness and height of the web on the trough girder structure noise is discussed.The results show that increase of the thickness of the bottom plate can reduce the structure noise of the trough girder,but it does not mean that the thicker the bottom plate is,the better the noise reduction effect is.When the thickness of the bottom plate reaches a certain value,its influence on the noise reduction effect of the structure is limited.Variation of the web height can alter the direction of radiation attenuation of the bridge structure noise,and the structure noise radiation on both sides of the bridge attenuates fast.The radiation noise of the structure above the bottom plate is the strongest,but it has a tendency to decrease with the variation of the web height.The results of the analysis can provide some theoretical references for the optimal design of the rail transit trough beam structure.

vibration and wave;coupled vibration;joint simulation;structure noise;finite element;indirect boundary element

U491.91；U270.16

：A

：10.3969/j.issn.1006-1335.2016.06.026

1006-1355(2016)06-0131-05

2015-10-25

國家自然科學基金資助項目（51268014，51578238)；江西省“贛鄱英才555工程”領軍人才培養計劃資助項目

曾峰（1992-），男，湖南邵陽人，碩士研究生，主要研究方向為鐵路環境振動與噪聲。E-mail:316058254@qq.com

劉林芽（1973-），男，教授，博士，博士生導師。