拉索-磁致伸縮作動器系統(tǒng)PID控制仿真分析

王修勇，李建強，孫洪鑫，方 聰

（湖南科技大學(xué) 土木工程學(xué)院，湖南 湘潭 411201）

拉索-磁致伸縮作動器系統(tǒng)PID控制仿真分析

王修勇，李建強，孫洪鑫，方 聰

（湖南科技大學(xué) 土木工程學(xué)院，湖南 湘潭 411201）

拉索的大幅振動給斜拉橋安全運營帶來威脅，利用磁致伸縮作動器施加軸向控制力抑制拉索橫向振動是一種可行的方法。首先建立磁致伸縮作動器動力學(xué)模型，得到了該作動器力-位移傳遞函數(shù)，然后提出拉索-磁致伸縮作動器系統(tǒng)PID控制算法，根據(jù)拉索振動幅度大小通過調(diào)節(jié)PID控制參數(shù)，來施加軸向控制力，達到對拉索的控制效果。最后針對自由振動、簡諧激勵、隨機激勵三種情況用PID控制算法對拉索-磁致伸縮作動器系統(tǒng)進行了拉索控制效果仿真分析。研究表明，PID控制算法對拉索振動具有很好的控制效果。

振動與波；拉索；磁致伸縮作動器；PID控制算法；仿真

斜拉索是具有初應(yīng)力的柔性結(jié)構(gòu),在使用狀態(tài)過程中由于環(huán)境激勵(風(fēng)、雨、結(jié)構(gòu)振動、汽車荷載)的作用,會產(chǎn)生各種形式的有害振動[1-2]。典型拉索振動包括風(fēng)致渦激振動、尾流馳振、風(fēng)雨導(dǎo)致的風(fēng)雨振以及支承擾動引起的參數(shù)振動等。抑制拉索大幅振動的方法主要有設(shè)置輔助索[3]、改變拉索氣動特性[4]、安裝阻尼器[5-6]、主動與半主動控制[7-8]等。主動與半主動控制的機理是通過改變拉索阻尼及剛度進行拉索振動控制，對各種拉索振動都能起到控制效果。針對拉索主動控制，一些學(xué)者也做了大量的研究，Yamaguchi等[9]提出了通過直接施加橫向力來控制拉索振動，但在橫向施力點會產(chǎn)生彎曲應(yīng)力，可能會導(dǎo)致拉索疲勞問題；Fujino[10]、Susumpow[11]、Warnitchai[12]、Achkire[13]等通過壓電作動器在拉索錨固端施加沿拉索軸向的控制力來控制拉索的振動，并開展了試驗研究；Gattulli等[14]同樣也采用壓電作動器在拉索錨固端施加軸向控制力來控制拉索振動，提出了多點優(yōu)化控制的方法，并進行了仿真和試驗研究；周海俊、孫利民等[7]采用智能材料形狀記憶合金提供軸向控制力，對斜拉索風(fēng)雨振控制進行了仿真研究；朱保兵、李國強[15]對不同邊界條件下拉索振動進行了主動控制研究；王修勇等[8]采用磁致伸縮作動器提供軸向控制力，進行了拉索主動控制與半主動控制仿真研究。由于拉索系統(tǒng)的動力復(fù)雜性和強非線性，難以建立起精確的模型，這將影響其控制效果。PID控制算法是控制工程中應(yīng)用最為廣泛的控制算法，具有原理簡單，使用方便，適應(yīng)性強，魯棒性強等特點，因此在解決拉索振動控制問題方面具有優(yōu)勢。在磁致伸縮作動器振動控制與PID控制算法研究方面，代建波等[16]采用超磁致伸縮作動器對大跨空間結(jié)構(gòu)地震響應(yīng)主動控制進行了仿真分析；胡均平等[17]采用超磁致伸縮作動器和模糊PID控制方法對機床的振動干擾進行了主動控制研究；張?zhí)祜w等[18]在結(jié)構(gòu)振動控制過程中利用超磁致伸縮作動器來減小結(jié)構(gòu)振動，進行了PID算法研究；畢泗坤[19]對由MR阻尼器提供控制力的拉索進行了半主動神經(jīng)網(wǎng)絡(luò)PID控制研究。基于PID控制算法的優(yōu)點以及拉索控制的復(fù)雜性，研發(fā)磁致伸縮作動器，建立其動力學(xué)模型，采用磁致伸縮作動器來提供軸向控制力，提出PID拉索振動控制算法，根據(jù)拉索振動幅度大小通過調(diào)節(jié)PID控制參數(shù)，來施加軸向控制力，達到拉索控制效果，并進行仿真分析，獲得良好控制效果。

1 磁致伸縮作動器模型

超磁致伸縮材料（GMM）是一種新型功能材料，在磁場作用下具有磁致伸縮現(xiàn)象、倍頻效應(yīng)、預(yù)壓應(yīng)力特性、遲滯現(xiàn)象、高頻特性差、溫度敏感現(xiàn)象以及力-磁耦合呈非線性。根據(jù)磁致伸縮材料的特性，設(shè)計制造出一款磁致伸縮作動器，其設(shè)計參數(shù)見表1，外形見圖1，內(nèi)部結(jié)構(gòu)見圖2。磁致伸縮作動器的工作原理見圖3，磁致伸縮棒在磁場作用下能輸出位移和作用力，其力學(xué)模型如圖4所示。

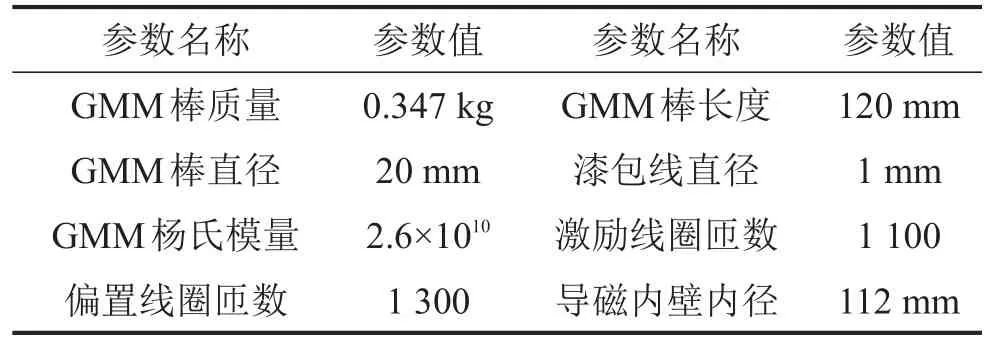
表1 超磁致伸縮作動器的部分參數(shù)表

圖1 磁致伸縮作動器外部構(gòu)造

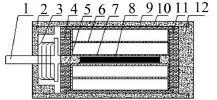
圖2 磁致伸縮作動器內(nèi)部結(jié)構(gòu)圖

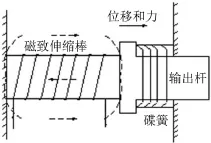
圖3 磁致伸縮作動器的工作原理圖

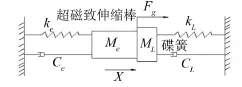
圖4 作動器力學(xué)模型

模型參數(shù)：Me為磁致伸縮棒的等效質(zhì)量；Ml為出力桿和碟簧的質(zhì)量；Ce為磁致伸縮棒的阻尼系數(shù)；Cl為碟簧的阻尼系數(shù)、Ke為磁致伸縮棒的等效剛度、Kl為碟簧剛度。x為伸縮棒伸長位移；Fg為磁致伸縮棒的輸出力

由圖4中作動器的力學(xué)模型，考慮GMM棒等效質(zhì)量和等效阻尼的影響，再由牛頓第二定律可得

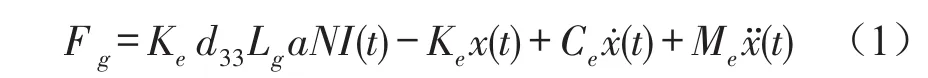
式（1）中N為螺線管線圈匝數(shù)，Lg為GMM棒的長度，d33為壓磁系數(shù)，a為磁場強度系數(shù)。

由圖4中作動器的力學(xué)模型，考慮輸出桿以及碟簧部分，則輸出桿的運動方程為

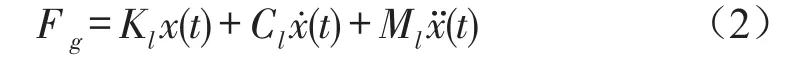
根據(jù)式（1）和式（2）得到作動器的電磁-機械耦合方程為

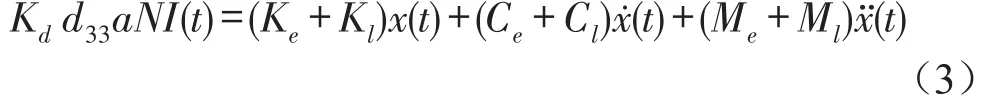
令F=Ked33LgaNI0/M，式（3）變?yōu)?/p>

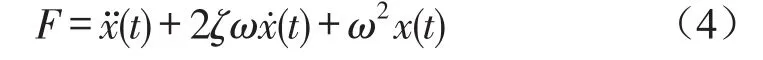
對式（4）進行拉普拉斯變化，可求得磁致伸縮作動器傳遞函數(shù)為

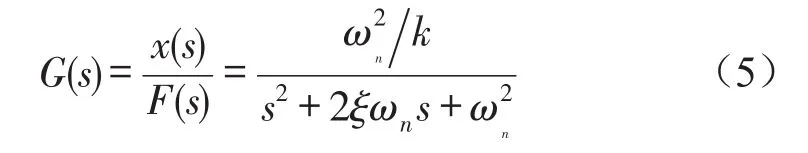
根據(jù)表1中的參數(shù)，考慮施加偏置磁場和預(yù)壓力后GMM棒材料近似符合線性特性，取代入式（5）得系統(tǒng)的固有頻率系統(tǒng)的阻尼比

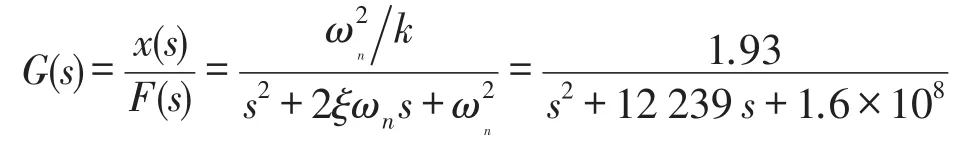
2 拉索面內(nèi)軸向主動控制方程

施加拉索軸向控制力，可以對拉索橫向振動進行控制，拉索控制系統(tǒng)力學(xué)模型如圖5所示。

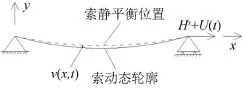
圖5 拉索軸向控制模型

設(shè)靜平衡狀態(tài)下初始索力為Hs，拉索沿軸向的主動控制力為U(t)，拉索單位長度質(zhì)量為m，不考慮拉索抗彎剛度和垂度影響，在外部激勵f(x,t)作用下其無阻尼運動方程為

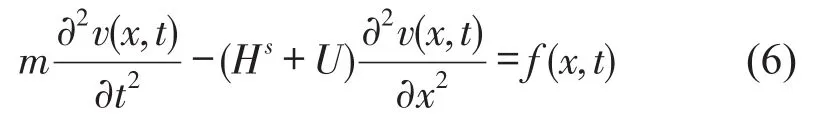
式中v(x,t)為拉索的動位移，可表示為

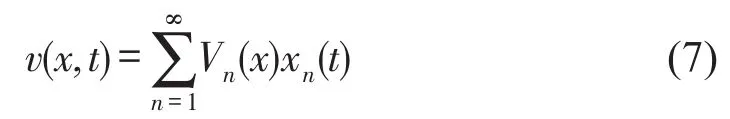
式中Vn(x)為第n階振型，xn(t)為第n階模態(tài)坐標。

將式（7）代入式（6），考慮到模態(tài)正交性可以得到n個獨立的振動方程。其振動方程的矩陣形式為

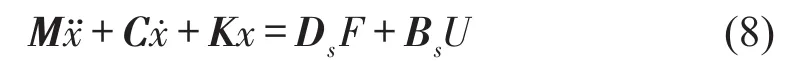
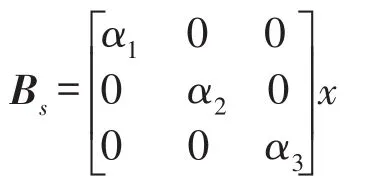
將式（8）采用狀態(tài)方程描述

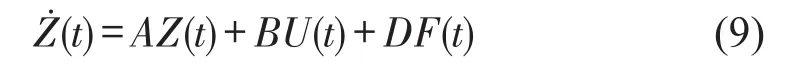
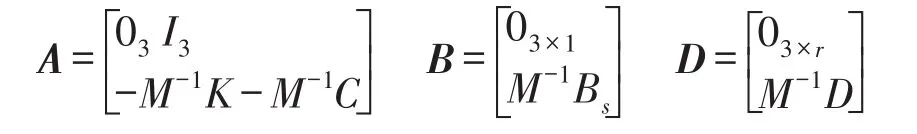
其中下標表示矩陣維數(shù)，r為激勵個數(shù)。

由于拉索系統(tǒng)狀態(tài)矩陣B跟Bs有關(guān)，對拉索系統(tǒng)狀態(tài)方程施加輸入時，B矩陣是與狀態(tài)變量有關(guān)系的，所以采用LQR算法，對拉索控制的整個過程采用分步迭代的方法可以求得每個時刻B，然后對整個時刻B求平均值，用這個值代替時刻變化的值。比較這兩種情況下拉索的減振效果，發(fā)現(xiàn)用每步變化值計算得到減振率為76.14%，采用平均值計算得到拉索減振率為75.01%，從減振效果來看，可以代替。

3 基于磁致伸縮作動器的拉索振動控制系統(tǒng)仿真

3.1 拉索PID控制仿真方法與模型拉索參數(shù)

PID(Percent-Integrate-Derivative)控制算法在工程中應(yīng)用廣泛，通過將輸入與被控對象的輸出之間的誤差作為控制器的輸入，將誤差的比例、積分和微分進行線性組合，通過調(diào)整各部分的作用大小來構(gòu)成控制量從而達到對被控結(jié)構(gòu)的控制作用。基于Simulink建立了拉索-磁致伸縮作動器系統(tǒng)PID振動控制仿真流程，分析各種激勵下的振動控制效果。

模型拉索以湖南岳陽洞庭湖大橋A10拉索為原型，按照索長縮尺20:1，建立前3階頻率基本一致的簡化拉索模型并進行仿真研究。具體參數(shù)見表2。

拉索有控條件下振動控制效率定義為

表2 模型拉索的主要參數(shù)[8]

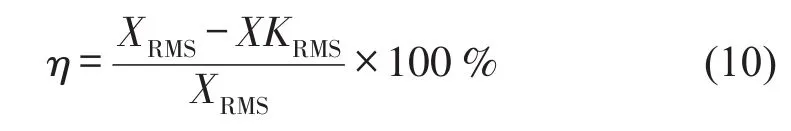
式中XKRMS為有控條件下拉索的位移RMS值，XRMS為無控條件下拉索的位移RMS值。

3.2 拉索主動控制仿真結(jié)果與分析

工況1——簡諧激勵

考慮拉索前3階模態(tài)，假定拉索結(jié)構(gòu)在l/4處作用一個最大值為6 N、RMS值大小為4.3 N的簡諧荷載。得到的拉索第1階模態(tài)位移時程曲線見圖6，第2階模態(tài)位移時程曲線見圖7，第3階模態(tài)位移時程曲線見圖8，控制力時程曲線見圖9，拉索2/5處位移時程圖見圖10，拉索1/4處位移時程圖見圖11。

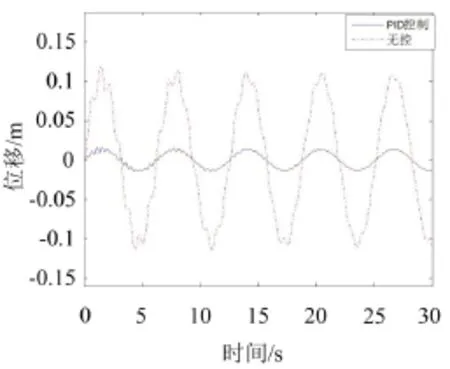
圖6 第1階模態(tài)位移時程圖

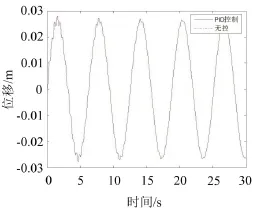
圖7 第2階模態(tài)位移曲線圖

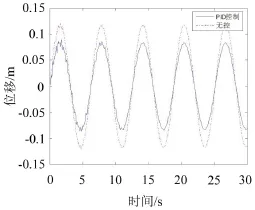
圖8 第3階模態(tài)位移曲線圖

從圖6—圖8可以看出，對于拉索第1和第3階模態(tài)，PID控制效果較好，但第2階控制效果較差。經(jīng)過模態(tài)組合，拉索在2/5和1/4處無控時RMS為0.074 8 m和0.078 3 m，PID控制時RMS為0.016 7 m和0.029 7 m。在30 s內(nèi)，拉索在2/5和1/4處進行PID控制，減振效率分別為78.7%和62.07%。

工況2——自由振動

考慮拉索前3階模態(tài)，假定拉索結(jié)構(gòu)初始模態(tài)位移為y1=0.06 m、y2=0.06 m和y3=0.06 m，初始速度為1=0 m/s、2=0 m/s和3=0 m/s。得到拉索2/5處位移時程圖見圖12，拉索1/4處位移時程圖見圖13。

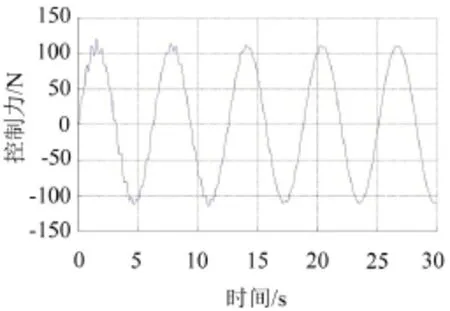
圖9 控制力時程曲線圖

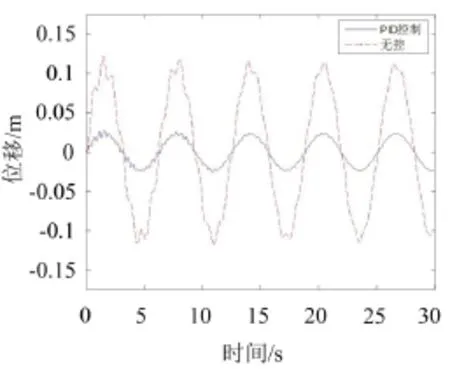
圖10 拉索2/5處時程曲線圖

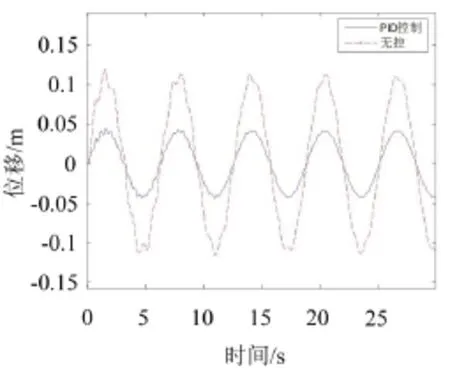
圖11 拉索1/4處時程曲線圖

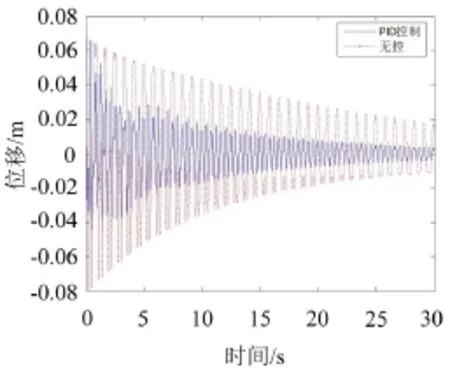
圖12 拉索2/5處位移時程曲線圖

由圖12、圖13可知，拉索在2/5和1/4處無控時RMS為0.027 8 m和0.027 5 m，PID控制時RMS為0.0126m和0.017 5 m。在30 s內(nèi)，拉索在2/5和1/4處進行PID控制，減振效率分別為54.68%和36.36%。

工況3——隨機荷載激勵

考慮拉索前3階模態(tài)，假定拉索結(jié)構(gòu)在l/4處作用一個最大值為2.186 3 N、RMS值大小為0.719 4 N的隨機荷載。得到拉索2/5處位移時程圖見圖14，拉索1/4處位移時程圖見圖15。

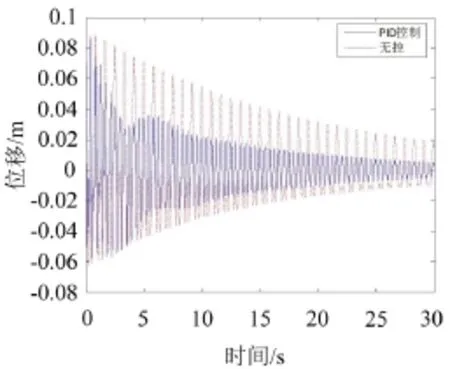
圖13 拉索1/4處位移時程曲線圖

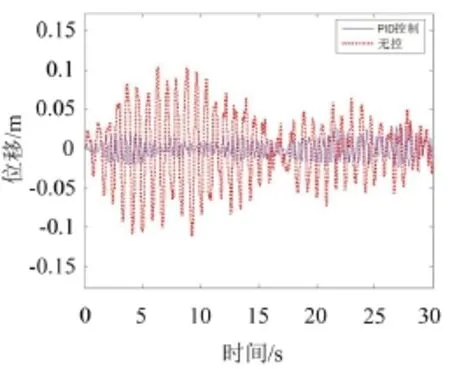
圖14 拉索2/5處位移時程曲線圖

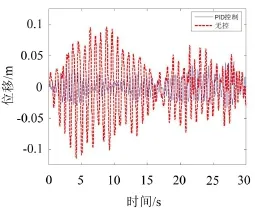
圖15 拉索1/4位移處時程曲線圖

從圖14、圖15可知，拉索在2/5和1/4處無控時RMS為0.010 1 m和0.043 1 m，PID控制時RMS為0.013 9 m和0.041 2 m。在30 s內(nèi)，拉索在2/5和1/4處進行PID控制，減振效率分別為76.57%和66.26%。

4 結(jié)語

采用磁致伸縮作動器進行拉索振動控制，推導(dǎo)出磁致伸縮作動器的力—位移傳遞函數(shù)，提出拉索-磁致伸縮作動器系統(tǒng)PID控制算法，進行前3階模態(tài)控制的拉索振動控制仿真研究。得到以下主要結(jié)論：

（1）在自由振動、簡諧激勵或隨機激勵等不同激勵作用下，PID控制都能取得良好的拉索振動控制效果。

（2）基于PID控制算法，三種不同工況情況下，第2階模態(tài)位移控制效果差，說明軸向控制力對反對稱振型控制效果差，但拉索整體控制效果良好。

[1]PACHECO B M,FUJINO Y.Keeping cables calm[J].Civil Engineering Magazine,1993,63(10):56-58.

[2]SAVOR Z,RADIC J,HRELJA G.Cable vibrations at dubrovnik bridge[J].Bridge Structures,2006,2(2):97-106.

[3]易圣濤.斜拉橋拉索防護現(xiàn)狀[J].重慶交通學(xué)院學(xué)報，2000，19(2)：11-14.

[4]陳艾榮，馬如進，王達磊.千米級斜拉橋空氣動力學(xué)問題[J].中國工程科學(xué)，2009，11(3)：31-37.

[5]XU Y L,YU Z.Non-linear vibration of cable-damper system part II:application and verification[J].Journal of Sound and Vibration,1999,225(3):465-481.

[6]王修勇，陳政清.確定斜拉索減振阻尼器優(yōu)化參數(shù)的一種方法[J].振動與沖擊，2002，21(1)：89-106.

[7]周海俊，孫利民.斜拉索風(fēng)雨激振的形狀記憶合金半主動控制數(shù)值模擬分析[J].防災(zāi)減災(zāi)工程學(xué)報，2008，28 (3)：308-312.

[8]王修勇，孟慶甲，郭雪濤，等.基于磁致伸縮作動器的拉索主動控制與多級Bang-Bang控制仿真分析[J].地震工程與工程振動，2014，34(2)：161-166.

[9]YAMAGUCHI H,DUNG N N.Active waves control of sagged-cable vibration[C].Proc.1stInt.Conf.Motion and Vibration Control,Yokohama,7-11 Sept.1992:134-139.

[10]FUJINO Y,WARNITCHAI P,PACHECO B M.Active stiffness control of cable vibration[J].Journal of Applied Mechanics,ASME,1993,60(4):948-953.

[11]SUSUMPOW T,FUJINO Y.Active control of multimodal cable vibrations by axial support motion[J].Journal of Engineering Mechanics,ASCE,1995,121(9):964-972.

[12]WARNITCHAI P,FUJINO Y,SUSUMPOW T.A nonlinear dynamic model for cables and its application to a cable structure system[J].Journal of Sound and Vibration,1995,187(4):695-712.

[13]ACHKIRE Y,PREUMONT A.Active tendon control of cable-stayed bridges[J].Earthquake Engineering and Structural Dynamics,1996,25:585-597.

[14]GATTULLI V,ALAGGIO R,POTENZA F.Analytical prediction and experimental validation for longitudinal control of cable oscillations[J].International Journal of Non-Linear Mechanics,2008,43(1):36-52.

[15]朱保兵，李國強.不同邊界條件下拉索振動的主動控制研究[J].力學(xué)季刊，2009，30(3)：461-468.

[16]代建波，王社良，趙祥.結(jié)構(gòu)地震響應(yīng)控制的優(yōu)化方法[J].噪聲與振動控制，2015，35(1)：42-47.

[17]胡均平，鄭聰，李科軍，等.精密機床的模糊PID主動隔振系統(tǒng)研究[J].噪聲與振動控制，2015，35(4)：193-197.

[18]張?zhí)祜w，汪鴻振，孫曜.超磁致伸縮作動器用于振動主動控制中的仿真研究[J].振動與沖擊，2006，25(1)：61-63.

[19]畢泗坤.拉索振動的MR阻尼器半主動神經(jīng)網(wǎng)絡(luò)PID控制應(yīng)用研究[D].濟南：山東輕工業(yè)學(xué)院，2011.

SimulationAnalysis of PID Vibration Control of Cables Using Giant MagnetostrictiveActuators

WANG Xiu-yong,LI Jian-qiang,SUN Hong-xin,FANG Cong
(School of Civil Engineering,Hunan University of Science and Technology, Xiangtan 411201,Hunan China)

Large amplitude vibration of stay cables can bring a great threat to the operation of the cable-stayed bridge. Using axial force provided by a giant magnetostrictive actuator(GMA)is a feasible method for cable vibration suppression. In this paper,the dynamic model of the GMA is established.And the actuator’s force-displacement function is obtained. Then,the PID control algorithm of the stay cable and the GMA coupling is proposed.Finally,simulation analyses of the stay cable under free vibration,harmonic excitation and random excitation are carried out.The result proves that the vibration of the cable can be controlled effectively by PID control algorithm.

vibration and wave;stay cable;giant magnetostrictive actuator;PID control algorithm;simulation

TU352

：

：10.3969/j.issn.1006-1335.2016.06.023

1006-1355(2016)06-0116-05

2016-06-08

國家重點基礎(chǔ)研究發(fā)展計劃資助項目（973計劃）(2015CB057702)；國家自然科學(xué)基金資助項目(51378203)

王修勇（1962-），男，博士，教授，湖南省新化市人，主要從事結(jié)構(gòu)振動控制研究。E-mail:xywang_cs@sina.com

李建強（1991-），男，碩士，甘肅省天水市人，主要從事結(jié)構(gòu)振動控制研究。E-mail:694191527@qq.com