有界窄帶激勵柴油機軸系扭振系統主參數共振

楊志安，卞雅媛

（1.唐山學院 唐山市結構與振動工程重點實驗室，河北 唐山 063000；2.華北理工大學 機械工程學院，河北 唐山 063000）

有界窄帶激勵柴油機軸系扭振系統主參數共振

楊志安1，卞雅媛2

（1.唐山學院 唐山市結構與振動工程重點實驗室，河北 唐山 063000；2.華北理工大學 機械工程學院，河北 唐山 063000）

研究柴油機軸系扭振強非線性系統在有界窄帶激勵下的主參數共振響應和穩定性問題。應用改進多尺度法得到在有界窄帶隨機激勵下柴油機軸系扭振系統的幅頻響應方程，導出系統的Ito隨機微分方程。通過矩法得到系統隨機均方響應的近似表達式，分析各個參數對柴油機軸系扭振系統主參數共振均方值的影響。結果表明，主參數共振穩態解穩定的充分必要條件與系統二階矩穩定的充分必要條件是一樣的；隨著阻尼值的增大，系統主參數共振振幅的均方值減小；隨著曲軸扭轉剛度的減小，系統主參數共振的均方響應曲線的斜率增大；隨著隨機擾動強度的增大，系統時間響應曲線和相圖變化微小。

振動與波；柴油機軸系扭振系統；窄帶激勵；改進多尺度法；主參數共振；均方響應

船用柴油機軸系扭轉振動是影響船舶安全運行和舒適運行的重要因素。嚴重的扭轉振動會造成曲軸、中間軸、螺旋槳軸斷裂，齒輪磨損，噪聲過大等危害，這些危害將影響船舶的安全航行。隨著大功率船用柴油機在大型船舶的應用，軸系扭振狀態也更加復雜，因此船用柴油機軸系扭振的研究變得更加重要[1]。

文獻[2]研究了柴油機扭振機理和傳動軸系扭振機理，并提出了針對船舶軸系的扭振測量方法。文獻[3]研究了柴油機軸系受氣體沖擊力與水沖擊動力作用的非線性扭轉振動問題，通過多尺度法得到了在飛輪勻速運轉條件下柴油機軸系受水沖擊動力引起的主參數共振的幅頻響應方程。文獻[4]應用拉格朗日方程，得到柴油機軸系受膨脹氣體沖擊力作用的非線性扭轉振動微分方程。根據多尺度法，得到主參數共振的幅頻響應曲線。文獻[5]研究了Duffing振子在窄帶隨機噪聲激勵下的主共振響應和穩定性問題。應用多尺度法得出了系統的阻尼項、隨機項等對系統響應的影響，文獻[6]研究環形極板機電耦合系統的強非線性問題，建立環形極板機電耦合系統的動力學方程，應用改進多尺度法求得系統的主共振的幅頻響應曲線，分析了不同的系統參數對共振的影響。

在以上柴油機軸系扭振系統的研究中，對確定激勵下的弱非線性振動問題進行了分析，但沒有考慮隨機激勵對柴油機軸系扭振強非線性系統的影響，而實際上外激勵存在相位、幅值的微小隨機變化。采用有界噪聲模型化窄帶隨機激勵特征，運用改進多尺度法分析窄帶隨機激勵作用下的主參數共振，得到系統隨機均方響應的近似表達式，分析比較其中各元素對均方值與共振區間的影響，對柴油機軸系扭振系統的設計與優化具有一定的參考價值。

1 柴油機軸系扭振系統非線性動力學方程

柴油機軸系單自由度系統由飛輪、氣缸及曲軸三部分組成，如圖1所示。

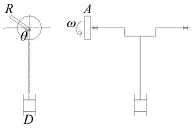
圖1 柴油機軸系簡圖

其中A為飛輪；M表示往復部分總質量，I為氣缸連桿旋轉部分總轉動慣量，ρ為阻尼，扭轉角為θ；飛輪轉動慣量為I1，曲柄半徑為R；氣缸直徑為D；飛輪的角速度為ω,角位移為θ1=ωt，曲軸角位移為θ=ωt+γ；曲軸扭轉剛度為μ；柴油機軸系扭振系統所受干擾力為膨脹氣體對活塞的沖擊力矩Ksin(nθ1+φ)，其中φ為沖擊力矩相位角[7]，K為簡諧力矩幅值，n為簡諧次數（即簡諧力矩在曲軸一轉時間里的變化周期數）；柴油機的轉速為N。

柴油機軸系模型如圖1所示，根據拉格朗日方程可以建立其非線性動力學方程[8-9]，但分析系統的主參數共振時，不考慮外激勵項影響，因此系統主參數共振的非線性動力學方程為[10]

2 主參數共振分析

應用改進的多尺度法研究V≥0且遠小于1時的情形。多尺度法已廣泛應用于確定激勵振動問題的研究中，近幾年在隨機振動問題中也有一定的應用[11-13]。故式（1）變為

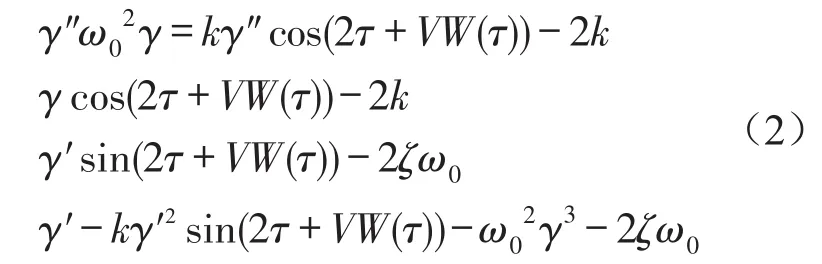
式中W(τ)為標準的Winner過程，V為隨機的擾動強度。

在式（2）中各參數激勵項和非線性項前引入非小量參數ε，方程變為

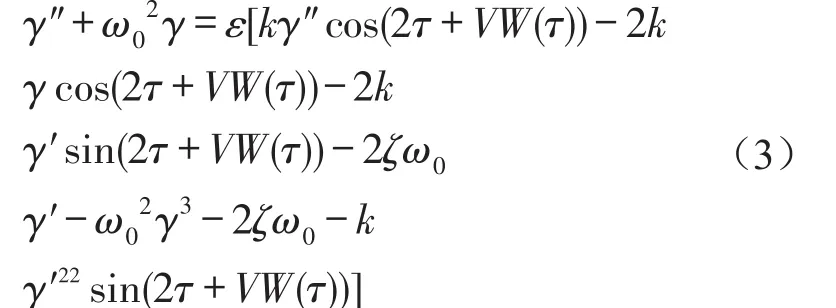
設Ω=2

令

引入參數變換

則有

把小參數α引入到多尺度方法中，設式（3）的一次近似解為

將式（6）、式（7）代入式（3）后，比較α同次冪系數，可得到消除永年項的條件，并根據歐拉公式分離實虛部可得

式（8）的精確解可以采用攝動法求得，但V很小，這里假設V=0，則式（8）變為

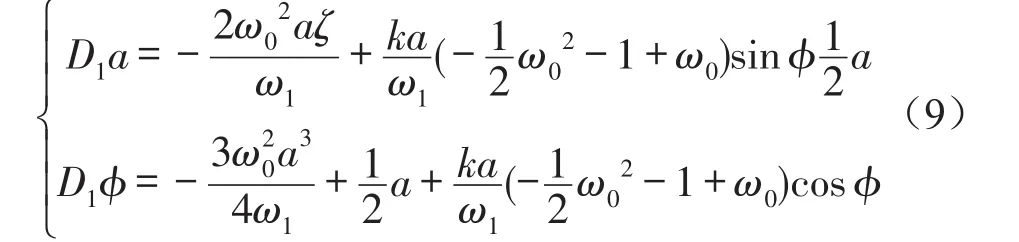
對于穩態振動a=a0，φ=φ0，有D1a=D1φ=0。可得系統表達式（9）的幅頻響應方程

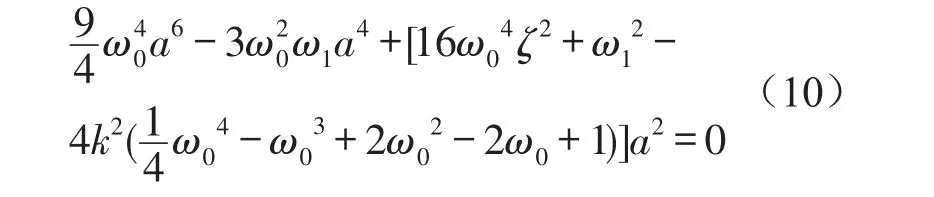
式中ω1為調諧值。

3 V≠0時穩定性條件

當V≠0時，由于V很小，可設方程式（8）的解為

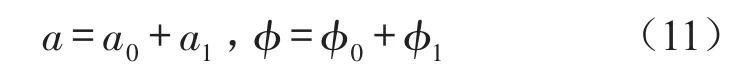
把D1a=D1φ=0代入式（9）可得a0和φ0，其中a1和φ1是攝動項，把式（11）代入式（8）中，不計關于a1和φ1的高階項，便得方程式（8）在定常解（a0，φ0）的線性方程為

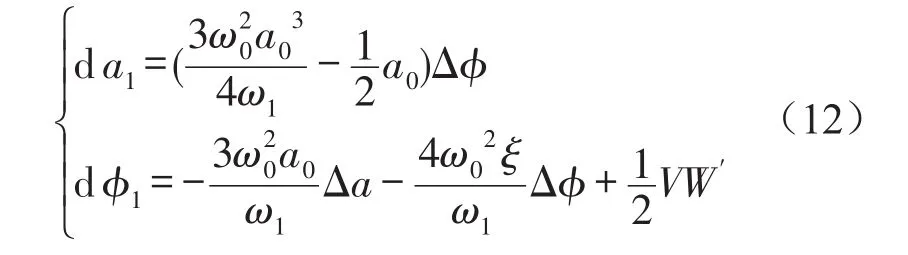
式中Δa為振幅擾動量；Δφ為相位擾動量；Wiener過程的導數W′是白噪聲的另一種表示方式，所以此方程組相當于線性系統在白噪聲外激勵下的響應問題。

依據Hurwitz定理可知[14]，該線性系統穩定的充要條件為

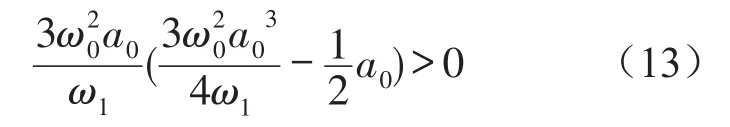
式（12）可寫成對應的Ito微分方程

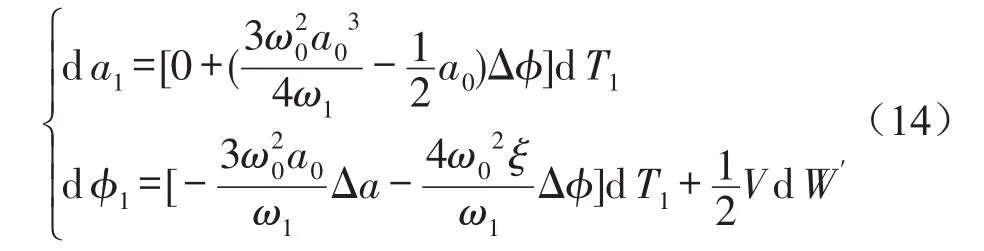
可用矩法求出式（14）的1階矩為

式（14）可寫成如下形式

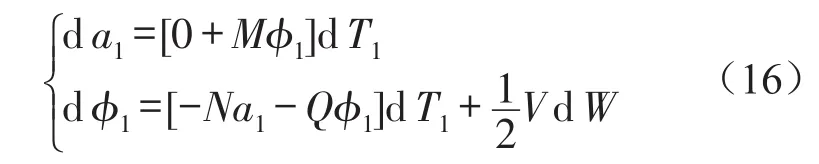
式中

以下各式中M、N和Q同上。

由Ito微分法則可得

整理式（17）得

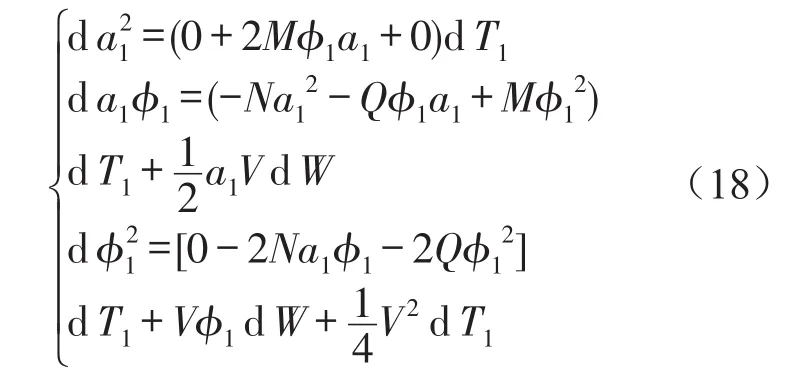
式（18）兩邊分別取期望，根據Ito微分法則可知

則式（18）可轉化為

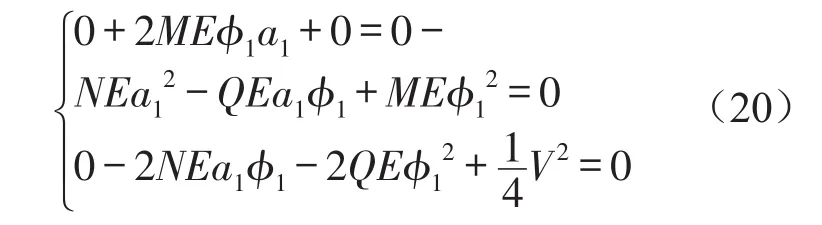
根據式（20）可知其系數矩陣為

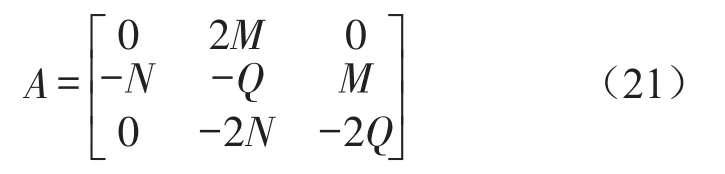
則

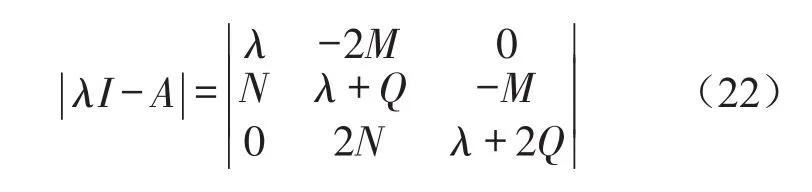
式（22）的特征方程為

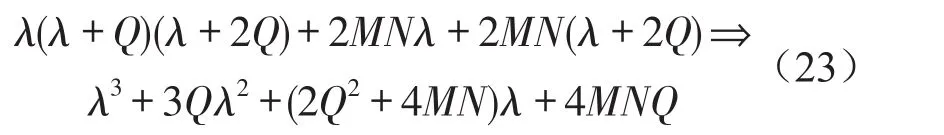
由式（23）可知

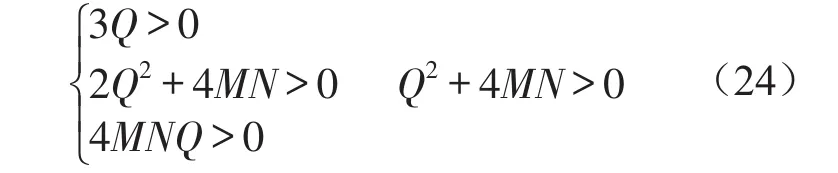
式（24）即為2階矩存在的充分必要條件，并與前面確定性系統（13）周期解的穩定性條件一致。a0的值與Ea2的值是相互對應的。

由式（20）可一次求得Ea12、，Ea1φ1、Eφ12的值

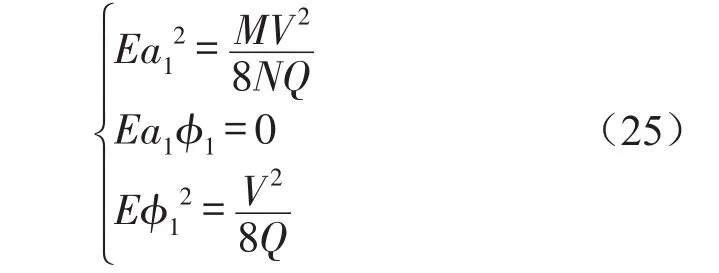
結合式（11）、式（15）和式（25）可得

4 數值模擬

S195型柴油機數值模擬采用的參數取值如下：M=1.995 kg，I=0.088 kg·m2，D=95 mm，R=57.5 mm，得出系統的響應。

圖2為V=0系統主參數共振的幅頻響應曲線，由于式（2）中的項系數相同，屬于強非線性問題，該曲線有兩個分支解。

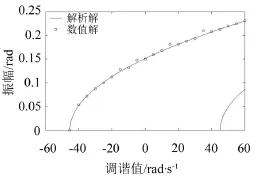
圖2 幅頻響應解析解和數值解的對比

一般龍格庫塔只能求時域信息，通過捕捉不同頻率下時域信息穩態解的振幅可以得到幅頻響應解，數值解與解析解進行對比，由圖2可得，數值解與解析解基本吻合。

圖3為柴油機軸系扭振系統主參數共振的均方響應曲線。由圖3可知，窄帶隨機激勵下主參數共振系統均方響應曲線與系統穩態解時幅頻響應曲線的拓撲結構相同，圖中粗實線部分為穩定解，細實線部分為不穩定解。

圖3 均方響應曲線

圖4為柴油機軸系扭振系統主參數共振在不同ρ值時的均方響應曲線。由圖4可知，隨著系統阻尼值的增大，系統主參數共振的均方值減小。

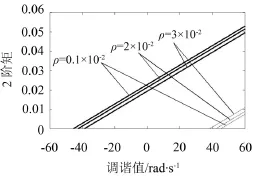
圖4 不同ρ值情況下均方響應曲線

圖5為柴油機軸系扭振系統主參數共振在不同μ值時的均方響應曲線。由圖5可知，隨著系統剛度值的減小，系統主參數共振的均方響應曲線的斜率增大。

圖5 不同μ值情況下均方響應曲線

5 主參數共振時間歷程分析

根據4階龍格-庫塔法用編寫程序得到系統表達式（3）的時間歷程曲線和相圖。

圖6為V=0時系統的時間歷程圖，由圖可知，隨著時間的增加，振動的最大位移逐漸趨于穩定。圖7為V=0時系統的相圖。

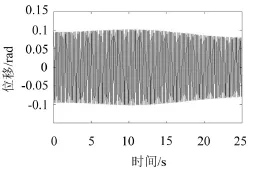
圖6 V=0時的歷程

圖8和圖9為V=0.01、V=0.1時系統主參數共振的時間響應曲線，對比圖8和圖9，可見得當V增大時柴油機軸系扭振系統的時間響應曲線變化不大。

圖10和圖11為V=0.01、V=0.1時系統主參數共振的相圖。對比圖10和圖11可得當V增大時柴油機軸系扭振系統的相圖極限環的厚度變化不大。

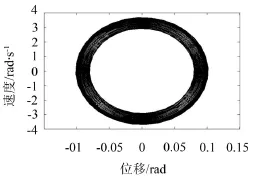
圖7 V=0時的相圖

圖8 V=0.01時的時間歷程

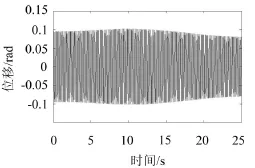
圖9 V=0.1時的時間歷程

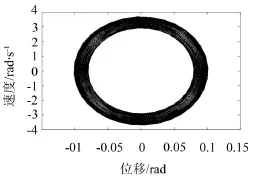
圖10 V=0.01時的相圖

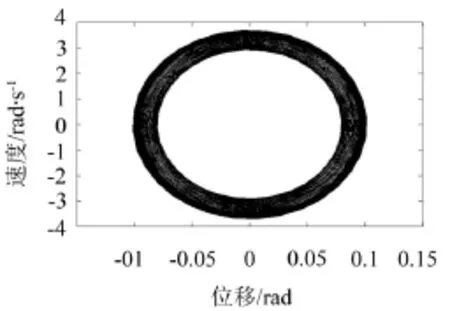
圖11 V=0.1時的相圖

6 結語

根據拉格朗日函數建立柴油機軸系扭振系統的動力學方程。應用改進多尺度法得到在有界窄帶隨機激勵下柴油機軸系扭振強非線性系統的響應，得到主參數共振的幅頻響應方程和系統均方響應的近似表達式，考慮了隨機項對響應的影響。理論分析與數值計算表明改變柴油機軸系扭振系統的參數，響應的均方值也隨之改變。結果表明，隨著阻尼值的增大，系統主參數共振振幅的均方值減小；隨著曲軸扭轉剛度的減小，系統主參數共振的均方響應曲線的斜率增大；隨著隨機擾動強度的增大，系統時間響應曲線和相圖變化不大；主參數共振穩態解穩定的充分必要條件與二階矩穩定的充分必要條件是一樣的。

[1]趙旭東.船用低速柴油機軸系扭振及其冰區特性的研究[D].大連：大連海事大學，2015.

[2]曾志龍.船舶軸系扭振應力測試技術研究[D].北京：中國艦船研究院，2014.

[3]楊志安，程欣桐.船用柴油機水沖擊動力作用軸系的主參數共振[J].工程力學，2013，30：333-337.

[4]楊志安，程欣桐.船用柴油機膨脹氣體沖擊力作用軸系的主參數共振[J].工程力學，2010，27(7)：221-225.

[5]戎海武，王向東，孟光，等.窄帶隨機噪聲作用下非線性系統的響應[J].應用數學和力學，2003，24(7)：723-729.

[6]楊志安，李熙，孟佳佳.改進多尺度法求解環形極板機電耦合強非線性系統主共振的研究[J].振動與沖擊，2015，34(9)：208-212.

[7]PASRICHA M S.Effect of damping on parametrically excited torsionalvibrationsofreciprocating engines including gas forces[J].Journal of Ship Resarch,2006, 50(2):147-150.

[8]肖能齊，周瑞平，林晞晨.含非線性部件的船舶推進軸系自由振動解析[J].噪聲與振動控制，2016，36(2)：135-138.

[9]程歐，茍向鋒.多自由度齒輪系統非線性動力學分析[J].噪聲與振動控制，2015，35(6)：31-35.

[10]程欣桐.考慮蒸汽力作用船舶柴油機軸系非線性振動研究[D].唐山：河北理工大學，2009.

[11]RONG HAI WU,XU WEI,FANG TONG.Principal Response of Duffing Oscillator to Combined Deterministic and Narrow-Band Random Parametric Excitation[J].Journal of Sound and Vibration,1998,210 (4):483-515.

[12]RONG HAI WU,MENG GUANG,FANG TONG.On the almost-sure asymptotic stability of second-order linear stochastic system[J].Journal Sound and Vibration, 2000,229(3):491-503.

[13]ZHU W Q.Stochastic jump and bifurcation of a duffing oscillatorundernarrow-bandexcitation[J].ActaMechanica Sinica,1994,01:73-81.

[14]朱位秋.隨機振動[M].北京：科學出版社，1992.

Primary Parametric Resonance of Shafting Torsional Vibration System of the Diesel Engine Subjected to Narrow-band Random Excitation

YANG Zhi-an1,BIAN Ya-yuan2
(1.Key Laboratory of Structure and Vibration Engineering of Tangshan,Tangshan College, Tangshan 063000,Hebai China; 2.College of Mechanical Engineering,North China University of Technology, Tangshan 063000,Hebai China)

The primary parameters resonance and stability problems of strong nonlinear torsional vibration of the diesel engine shafting system under narrow-band excitation are investigated.The frequency response equation of the system is obtained based on the modified multi-scale method and the corresponding Ito stochastic differential equation is derived.By means of the moment method,the approximate expression of the mean-square response of the system is obtained and the influence of the system parameters on the mean square value of the primary parametric resonance is analyzed.The results show that the sufficient and necessary conditions for the stability of primary parametric resonance are the same as those of the second order moment stability.With the increase of the damping,the mean square value of the resonant amplitude of the primary parameters of the system decreases;With the decrease of the torsional stiffness of the crankshaft,the slope of the mean square response curve of the system increases;Along with the increase of the random disturbance intensity,the time response curve and the phase diagram of the system only have small changes.

vibration and wave;shaftin torsional vibration system of diesel engineg;narrow-band random excitation; modified multi-scale method;primary parametric resonance;mean square response

0324

：ADOI編碼：10.3969/j.issn.1006-1335.2016.06.015

1006-1355(2016)06-0077-05

2016-05-05

河北省自然科學基金項目（A200900097）

楊志安（1963-），男，河北省秦皇島市人，博士，教授，碩士生導師，研究方向為機構學與機械動力學。E-mail:yangzhi_an@163.com

卞雅媛（1989-），女，河北省廊坊市人，碩士研究生，研究方向為機構學與機械動力學。E-mail:1198606508@qq.com