基于MATLAB的井下壓力計電子系統可靠性仿真

閆 建

(重慶三峽職業學院，重慶萬州 404155)

?

基于MATLAB的井下壓力計電子系統可靠性仿真

閆 建

(重慶三峽職業學院，重慶萬州 404155)

井下壓力計是油田壓裂作業過程中井下數據的重要測試與儲存裝置。針對傳統可靠性分析周期長、經濟性差的局限性，本文運用MATLAB軟件編寫電子系統仿真軟件，很好地解決了這一問題；通過仿真得到井下壓力計電子系統的仿真壽命為2877.7小時，并得到電子系統的可靠性曲線和累計失效率曲線；改變電子元器件初始失效率數據，分析得到可靠性曲線和累計失效率曲線的變化趨勢，由此推得井下壓力計電子系統可靠性的變化規律，這對于工程實踐具有重要指導意義。

井下壓力計；電子系統；可靠性；仿真

井下壓力計是油田壓裂增產最為常用的測井儀器，主要測量壓裂時井底的溫度和壓力。井下壓力計能否有效地采集數據，直接關系到對壓裂效果及開采率的評估。故井下壓力計是否能夠穩定、可靠地工作就顯得非常重要。傳統可靠性分析周期長、經濟性差，不能滿足企業的需求，隨著計算機的快速發展，數字仿真的出現創造性地解決了這一難題[1]。本文重點研究了井下壓力計電子系統的壽命和相關可靠性曲線的變化規律。

1 建立故障樹

井下壓力計電子系統失效，主要是由于單片機模塊、壓力信號采集與處理模塊、溫度信號采集與處理模塊、存儲器模塊和電池模塊故障引起。建立故障樹實際上也是對具體失效原因分析的一個總結。由于故障樹是以樹狀圖的形式來表達系統失效信息，因此它不僅能表現井下壓力計的失效事件，還能表現出各子部件之間功能上的邏輯關系。本文所建立的井下壓力計故障樹選取“井下壓力計失效”作為系統的頂事件，通過具體失效原因分析來展開故障樹，如圖1所示。

圖1中故障樹底事件對應元器件的失效特征參數都是由《GJB/Z 299C-2006》中的可靠性預計模型及失效參數計算得來[2]。具體失效率如表1所示。

2 可靠性仿真

2.1 仿真原理

步驟一，依次對故障樹最小割集所包含的底事件進行失效時間抽樣，獲得每個最小割集的失效時間；步驟二，比較最小割集的失效時間，取得它們的極小值，該極小值就是系統失效時間的一個抽樣值，這樣便完成了一次仿真；步驟三，重復步驟一、步驟二，得到系統失效時間的一個樣本，對樣本統計分析，得到系統可靠性曲線和壽命[3]。

本文所設計的井下壓力計所涉及的元器件只要有其中任何一個失效，系統都會失效，故可以知道本系統的每一個元器件都是一個最小割集。

圖1 井下壓力計電子系統故障樹模型

代碼底事件含義分布類型失效率/壽命次數X1單片機失效指數分布λ=12．01次/106小時X2電池失效指數分布λ=1．125次/106小時X3熱敏電阻失效指數分布λ=0．729次/106小時X4～X15R≤100Ω電阻失效指數分布λ=0．024次/106小時X16～X17R>100Ω電阻失效指數分布λ=0．039次/106小時X18～X22三極管失效指數分布λ=0．232次/106小時X23～X26壓敏電阻失效指數分布λ=0．648次/106小時X27～X34R≤100Ω電阻失效指數分布λ=0．024次/106小時X35～X36R>100Ω電阻失效指數分布λ=0．039次/106小時X37二極管失效指數分布λ=0．087次/106小時X38～X40三極管失效指數分布λ=0．232次/106小時X41～X48存儲器失效指數分布λ=13．22次/106小時

2.2 編寫仿真軟件

基于蒙特卡羅理論，利用MATLAB軟件編寫可靠性仿真軟件[4]。仿真軟件的算法流程如圖2所示。

具體說明如下：

第一，規定系統的最大工作時間為Tmax，將它等分成m個相等的時間間隔。每個時間間隔為ΔT，則有ΔT=Tmax/m。本文中規定Tmax=10000小時。

第二，規定仿真運行的次數N，本文仿真次數N=100000次。

第三，根據建立的故障樹模型，該故障樹有n個底事件，涉及系統的n個基本元器件。對于第i個基本元器件，其失效分布函數Fi(t)已知。

第四，前面已知第i個基本元器件的失效函數Fi(t)，其反函數就是該基本元器件的失效時間[5]。

(1)

其中，η為[0,1]區間上均勻分布的隨機數。通過該抽樣方法可以得到N次仿真系統的壽命矩陣T，該矩陣的維數為N×n，矩陣的每一行即為系統的一次仿真。再利用MATLAB提供的函數，求出每一次仿真的最小失效時間矩陣Ts，該矩陣的維數為N×1。

第五，仿真結束，對失效樣本進行統計分析，得到系統的各項可靠性指標。

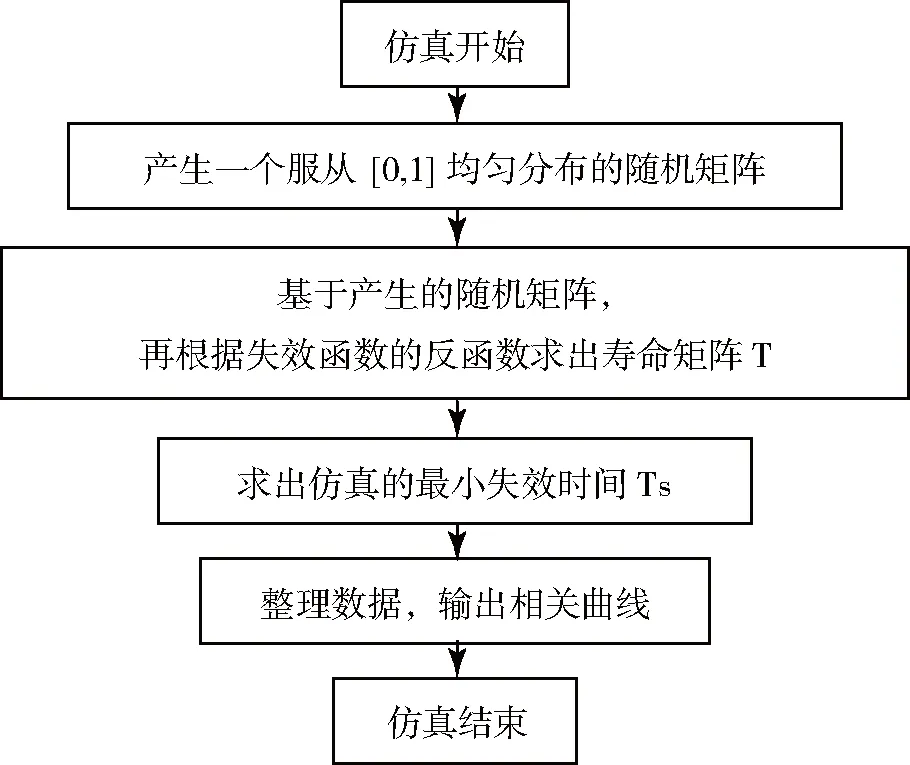
圖2 算法流程圖

3 仿真結果分析

3.1 累計失效率及變化規律

根據仿真的各項數據，再由公式(2)得到系統的累計失效率(不可靠度)曲線，如圖3所示[6]。

Fs(tr)=mr/N.

(2)

圖3 累計失效率(不可靠度)曲線

圖4 累計失效率系列曲線

在圖3中，橫軸表示仿真時間，縱軸表示累計失效率。隨著時間的增加，累計失效率不斷增大，逐漸趨近于1，與實際相符。

在圖4中，在其它元器件失效率不變的情況下，沿著箭頭方向的7條曲線分別是單片機失效率為1次/106小時，12次/106小時，22次/106小時，32次/106小時，42次/106小時，52次/106小時，62次/106小時的累計失效率系列曲線。隨著單片機失效率不斷增加，電子系統的累計失效率曲線不斷沿著箭頭的方向移動，即系統的累計失效率逐漸增大。當其它元器件失效率增加時，有著類似的規律。

3.2 可靠度及變化規律

由仿真數據，根據式(3)可得系統可靠度曲線，如圖5所示。

Rs(tr)=1-Fs(tr).

(3)

在圖5中，橫軸表示仿真時間，縱軸表示可靠度。隨著時間的增加，可靠度不斷減小，逐漸趨近于0，與實際相符。

在圖6中，在其它元器件失效率不變的情況下，沿著箭頭方向的7條曲線分別是單片機失效率為1次/106小時，12次/106小時，22次/106小時，32次/106小時，42次/106小時，52次/106小時，62次/106小時的可靠度系列曲線。隨著單片機失效率的不斷增加，電子系統的可靠度曲線不斷沿著箭頭的方向移動，即系統的可靠度逐漸減小。當其它元器件失效率增加時，有著類似的規律。

圖5 可靠度曲線

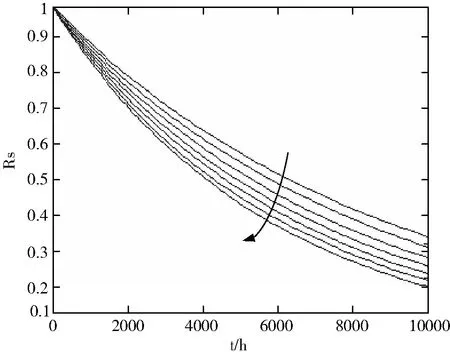
圖6 可靠度系列曲線

3.3 系統失效概率分布

由仿真數據，根據式(4)可得系統失效概率分布直方圖，如圖7所示。

(4)

圖7 系統失效概率分布直方圖

在圖7中，用直方圖表示了壓力計電子系統在壽命的不同時期的失效概率分布以及變化情況。橫坐標上每一個直方圖的跨距為100小時，縱軸是在仿真過程中失效事件分別落在不同時間區間的概率。電子壓力計的失效概率分布直方圖也是基本服從指數分布的。這也說明，電子元器件主要以指數分布的形式失效，與理論相符合。

3.4 系統壽命

根據仿真數據，再由公式(5)可以得到系統的壽命。

(5)

通過公式(5)處理得到系統平均無故障工作時間為2877.7小時左右。按壓力計下到井下后每天24小時計算，可連續工作約120天，完全滿足壓裂作業對壓力計的要求。

4 結論

首先，通過仿真得到井下壓力計電子系統的壽命大約為2877.7小時，按壓力計下到井下后，每天24小時計算，可連續工作約120天，完全滿足壓裂作業對壓力計的要求。由此也可以得出，電子元器件工藝本身能夠滿足井下壓力計的要求，而井下壓力計的失效往往是由于密封失效或者機械振動所導致。

其次，在沒有冗余設計的情況下，隨著電子元器件失效率的增加，系統累計失效率逐漸增大，系統可靠度逐漸減小，系統壽命逐漸減小。

[1]P.M.Hannah,K.L.Vekved.Precision pressure measurement: the key to accurate Fluid-Interface monitoring [C].SPE Permian Basin Oil and Gas Recovery Conference,21-23March,Midland,Texas, 2000.

[2]曾紀科,韓常英.電子設備可靠性預計手冊[M].北京:科學出版社,2006:50-70.

[3]林鳳梅.故障樹分析及仿真方法在球磨機傳動系統中的應用研究[D].保定:華北電力大學,2003.

[4]羅華飛.Matlab GUI學習手記[M].北京:北京航空航天大學出版社,2009:271-302.

[5]石彬.基于故障樹的EPS系統可靠性及失效模式仿真研究[D].杭州:浙江大學,2007.

[6]王正林,劉明.精通MATLAB7[M].北京:電子工業出版社,2006:1-224.

Reliability Simulation of Electronic Systems of Downhole Pressure Gauge Based on MATLAB

YAN Jian

(Chongqing Three Gorges Polytechnic College, Wanzhou Chongqing 404155,China)

Downhole pressure gauge is an important test and data storage devices during downhole oilfield fracturing. Aim at the long cycle and poor economic limitations of traditional reliability analysis, this paper solved the problem by writing simulation software used MATLAB.To obtain life of electronic systems of downhole pressure gauge is 2877.7 hours and associated reliability curve.To get the trend of reliability curve by changing the initial failure rate of electronic components,and to get the reliability regulation of electronic systems. It has important guiding significance for engineering practice.

downhole pressure gauge; electronic systems; reliability; simulation

2016-06-23

閆 建(1988- )，男，講師，碩士研究生，從事機電系統測試傳感理論及信息處理研究。

TE319

A

2095-7602(2016)12-0029-05