平板和靜葉表面氣流-水膜耦合流動特性的數值研究

范小軍,李亮,李森,張翔

(1.西安交通大學能源與動力工程學院,710049,西安;2.中國航發商用發動機有限責任公司,200241,上海)

?

平板和靜葉表面氣流-水膜耦合流動特性的數值研究

范小軍1,李亮1,李森2,張翔2

(1.西安交通大學能源與動力工程學院,710049,西安;2.中國航發商用發動機有限責任公司,200241,上海)

針對平板表面的空氣水膜和透平靜葉柵中的水蒸氣水膜耦合流動特性提出了分析氣流與壁面水膜耦合作用的數值方法,即氣相主流和液相水膜視為相對獨立的開口系,通過在兩相各自的控制方程中添加考慮相間動量和能量交換的源項,實現水膜和氣流的雙向耦合計算。研究表明:平板表面水膜厚度和進口水膜雷諾數近似呈1/2指數冪關系,與來流馬赫數呈反比關系,與出口背壓呈弱負指數次冪關系;水膜流速與出口背壓近似呈線性關系;水膜附加損失對水膜流量的變化較為敏感,對來流馬赫數并不敏感;透平靜葉壓力面側水膜厚度分布較為均勻,在葉頂角區的葉片表面出現水膜聚積,吸力面側水膜厚度變化較為劇烈,在葉頂和葉根角區的葉片表面出現水膜聚積。從而得出影響透平葉柵通道中水膜分布的機理是,壁面曲率通過影響相間剪切力來影響壁面水膜厚度和速度的分布,端壁上從壓力面到吸力面的二次流引起水膜向吸力面側聚積,通道渦和角渦引起的徑向壓力梯度導致葉片表面水膜沿葉高重新分布,水膜聚積對葉片表面的壓力分布和出口氣流角產生顯著影響。

氣流;水膜;耦合流動特性;數值研究

葉輪機械中航空發動機吸雨[1]、燃氣輪機濕壓縮[2]以及蒸汽透平中的水蒸氣發生非平衡凝結[3]都會形成不同尺寸的液態水滴,這些水滴在慣性力[4]和湍流擴散作用[5]下沉積在葉輪機械的葉片和端壁表面且形成水膜。如圖1所示,水膜在相間剪切力、表面張力、固體表面摩擦力以及壓力梯度的作用下運動,部分水膜在葉片尾緣破碎形成大水滴。對于壓氣機,葉片表面水膜的存在顯著改變了氣流速度和落后角的徑向分布,使得級的氣動效率降低,工作穩定裕度下降[6];對于蒸汽透平,葉片和汽缸表面水膜的運動則引起葉片型面損失的增加和葉片的水蝕[3]。

圖1 壁面水膜流動示意圖

水膜和氣流之間的耦合作用是引起葉輪機械氣動性能變化的根本原因,為了深刻認識水膜出現時葉輪機械性能變化的原因與規律,必須深入了解葉輪機械中水膜和高速氣流之間耦合作用的機理。由于葉輪機械中水膜的厚度在數十微米的量級,目前水膜特性的實驗測量還存在很大困難,因此數值計算便成為了研究這一問題的有效手段。

Kirillov將葉片簡化為平板,最早建立了平板葉片表面水膜運動的方程,計算了不同安裝角下平板葉片表面水膜的運動軌跡[7]。Williams等將Kirillov的方法推廣到真實三維葉片表面水膜軌跡的計算中,在計算方法上取得突破[8]。但是,上述兩種方法都只能給出水膜的速度和軌跡,而不能給出水膜的厚度分布。Nikolaidis等基于三維計算流體動力學(CFD)氣動計算結果發展了壓氣機葉片表面水膜特性的計算程序[1],Fendler等對于透平發展了基于子午通流計算結果的水膜特性計算程序[9],這兩種方法能夠反映葉輪機械實際三維流動條件下葉片表面水膜速度和厚度分布的更多細節,但僅考慮了氣流對水膜的作用,仍然屬于單向耦合方法。

本文發展了葉輪機械中水膜和氣流耦合作用的數值計算方法,對平板表面的空氣-水膜流動以及葉柵通道中的水蒸氣-水膜流動進行了研究。

1 數值方法

假設氣相主流與壁面的液相水膜之間無相變引起的傳質過程,僅存在相間的動量和能量交換。將氣相主流和液相水膜視為相對獨立的開口系,通過在兩相各自的控制方程中添加考慮相間動量和能量交換的源項,實現水膜和氣流的雙向耦合計算。

1.1 流動控制方程

在葉輪機械中,氣流作用下壁面的水膜厚度遠小于壁面的曲率半徑,因此可以不考慮水膜沿壁面法向的運動。這樣,水膜在葉片和端壁三維曲面表面進行二維流動,流動控制方程為

(1)

A=[h,hVf,hTf]T

B=[hVf,hVfVf,hVfTf]T

式中:h為水膜厚度;Vf為水膜速度;Tf為水膜平均溫度;s為壁面梯度算子;A為虛擬時間推進項;B為平均通量項;Sf為源項;K為內部黏性項。Sf、K表達式分別為

(2)

(3)

動量源第一項-hsPL/ρf中的PL包含了氣相壓力項Pv、法向重力項Pg和表面張力項Pσ;動量源第二項gτh代表平行于水膜流動方向τ的重力分量;第三項3τfs/2ρf代表相界面處的氣流剪切力;內部黏性項中νf為水的黏性系數。相應表達式為

PL=Pv+Ph+Pσ

Pg=-ρfh(ng)

(4)

Pσ=-σs·(sh)

式中:ρf為水的密度;g為重力加速度;n為法向矢量;σ為表面張力。

能量方程源項中,Ts為相界面上的溫度,Tw為壁面溫度。水膜內的溫度可以認為沿壁面法向線性分布,在靠近壁面的h/2區域內水膜溫度由Tw變為Tf,在靠近相界面的h/2區域內水膜溫度由Tf變為Ts。

氣相的控制方程采用Navier-Stokes方程。對于笛卡爾坐標系下的三維黏性流動有

·D=F+Sv

(5)

式中:p、ρv、U、Ev分別為氣相的壓力、密度、速度和總能;Π為應力張量;F為黏性項;Sv為氣相源項。方程(1)、(5)和狀態方程構成了求解氣流與水膜雙向耦合流動的全部控制方程。

數值求解時借助商用軟件Fluent進行,其中氣相流動控制方程(5)由軟件直接求解,源項Sv通過軟件提供的用戶接口UDF添加。水膜流動控制方程(1)通過用戶接口UDS求解。空間離散采用二階迎風格式,氣相流動求解采用k-ω湍流模型。

1.2 數值方法驗證

Hammitt在水蒸氣風洞中對平板表面的水膜厚度進行了實驗研究[10],實驗段如圖2所示。平板前緣沿垂直流動方向布置了寬度為1 mm的注水縫隙,流出注水縫隙的水在氣流剪切力作用下的平板表面形成水膜;水膜厚度由布置在平板中心線上的電導傳感器1進行測量。

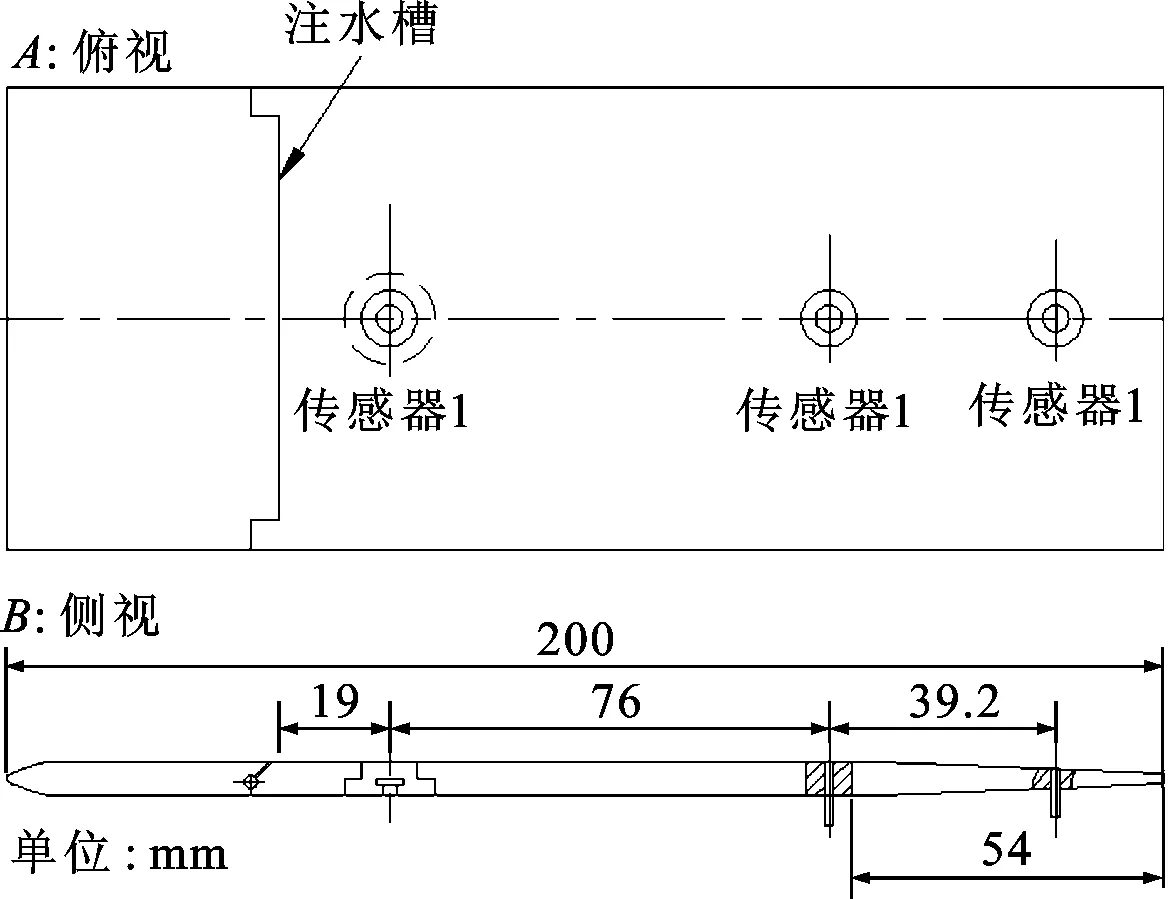
圖2 平板表面水膜實驗[10]

按照實驗段參數,建立了用于數值模擬的矩形通道模型。通道流動截面為30 mm×30 mm,軸向弦長c=100 mm,通道底面前緣設置了寬度為1 mm的注水縫隙。保持來流水蒸氣的溫度T0v=325.45 K、注水溫度T0f=325.45 K以及出口背壓P1=20 kPa不變,改變進口水蒸氣的流速和注水流量m對通道底面的水膜厚度進行了計算,并與文獻[10]中實驗數據擬合曲線進行了比較,結果如圖3所示。可以看到,本文數值計算的平板表面水膜厚度在水蒸氣流速約從50～200 m/s、水膜流量從10～70 cm3/min變化的范圍內與實驗測量結果一致。

圖3 平板表面水膜厚度分布

2 平板表面的空氣-水膜耦合流動

研究平板表面的空氣-水膜耦合流動是進一步分析復雜葉柵通道內水膜和氣流耦合流動特性的基礎。本節采用與上節相同的幾何模型,對不同來流馬赫數、出口背壓和水膜流量條件下的平板表面空氣-水膜耦合流動特性進行了研究。

2.1 氣流剪切力作用下的平板表面水膜流動特性

保持空氣進口溫度T0a=300 K,注水溫度T0f=300 K,對來流馬赫數Ma為0.1～0.6、進口水膜雷諾數Ref為33～188、出口背壓為0.05～0.25 MPa共48個工況條件下的平板水膜進行了計算。水膜雷諾數Ref定義為

Ref=ρfud/μf=Q/μf

(6)

式中:u為注水縫隙出口處液相的速度;d為注水縫隙的寬度;Q為水膜流量;μf為水的運動黏性系數。圖4給出了來流馬赫數Ma=0.4時不同水膜雷諾數下沿流向x/c(x為以進氣邊為原點的軸向坐標)水膜厚度和相間剪切力Lfs的變化。

圖4 平板表面水膜厚度和相間剪切力沿流向的分布

在注水縫隙處,由于水膜剛剛形成,其流向速度近似為0,此時相界面上的速度梯度最大,水膜厚度和相間剪切力均達到最大值;離開注水縫隙后,受氣流的剪切力作用,水膜流速增加而厚度減小,同時導致相界面上的速度梯度減小,相間剪切力隨之迅速減小;在遠離注水縫隙的下游,氣流處于充分發展的湍流區,相間剪切作用力逐漸下降并趨于穩定,因而水膜厚度緩慢增加并趨于穩定。隨著進口水膜雷諾數的增加,水膜厚度依次增加,但分布趨勢類似;相間剪切力的大小和分布基本不變。這表明相間剪切力主要受氣流馬赫數的影響,與水膜厚度基本無關。

為了分析水膜的厚度和平均速度與各影響因素之間的關系,圖5給出了x/c=0.8位置處水膜參數隨邊界條件的變化趨勢。在給定出口背壓P和水膜進口雷諾數時,水膜厚度和來流馬赫數近似呈反比關系(見圖5a),而水膜平均流速Vr與來流馬赫數呈線性關系(見圖5d)。在給定來流馬赫數和出口背壓時,水膜厚度和水膜平均流速與水膜進口雷諾數近似呈1/2指數冪關系(見圖5b、5e)。另外,

相

間剪切力與進口水膜雷諾數無關,而僅隨來流馬赫數變化(見圖5d)。在給定馬赫數和水膜雷諾數時,水膜厚度隨背壓的增加而減小,水膜速度則呈現增加的趨勢;背壓通過影響氣水分界面上的溫度來影響水膜的黏性系數μf,最終影響水膜的厚度和速度分布。

采用線性回歸方法對Ref=20～200范圍內水膜厚度與馬赫數、水膜雷諾數的關系進行了擬合,結果為

(7)

(8)

2.2 水膜對氣流總壓損失特性的影響

邊界層損失是內流損失的主要組成部分之一。當壁面存在水膜時,由于湍流邊界層的厚度遠遠大于當地水膜的厚度,所以水膜對主流的影響可以忽略,但其顯著影響邊界層內的流動。如圖6所示,當壁面存在水膜時,氣水分界面上水膜頂層受氣流的剪切力作用發生運動,同時消耗氣流的部分動能,因而可能影響氣流的總壓損失特性。

為了定量描述水膜對總壓損失特性的影響,定義有、無水膜時通道總壓損失系數比

(a)水膜厚度隨Ma的變化趨勢 (b)水膜厚度隨Ref的變化趨勢 (c)水膜厚度隨出口背壓的變化趨勢

(d)水膜平均流速隨Ma的變化趨勢 (e)水膜平均流速隨Ref的變化趨勢 (f)水膜平均流速隨出口背壓的變化趨勢圖5 x/c=0.8位置處水膜參數隨邊界條件的變化

圖6 有、無水膜時的邊界層流動

(9)

圖7 總壓損失特性隨馬赫數的變化規律

3 透平葉柵中的水蒸氣-水膜耦合流動

對某核電汽輪機末級靜葉柵中水蒸氣-水膜耦合流動進行研究。計算時采用結構化網格,經網格無關性驗證確定網格總數為230萬。邊界條件從葉柵所在的低壓透平全三維計算結果[12]中獲得。進口蒸汽流量為3.96 kg/s,總溫為337.971 K,進口湍流度為5%,出口壓力為16 618.2 Pa。葉片和上端壁表面水滴沉積形成水膜的流量分別為0.045 kg/(m2·s)和0.019 kg/(m2·s);葉片和上端壁表面水膜的初始平均厚度為45.7 μm;假設水滴撞擊壁面形成的水膜保留原始水滴速度的20%[1],則水膜的初始速度為47.62 m/s。

3.1 葉片和上端壁表面的水膜分布

圖8給出了主流水蒸氣作用下葉片表面水膜的分布。壓力面水膜厚度較為均勻,沿葉高方向大部分區域水膜厚度維持在25～35 μm范圍內;在葉頂與端壁交匯的角區,壓力面出現了帶狀的水膜聚積區,其厚度達到90 μm左右。與壓力面相比,吸力面水膜厚度的變化較為劇烈:在20%軸向弦長之前,吸力面水膜的厚度小于20 μm,且沿葉高方向基本不變,沿流動方向略有增加;在20%軸向弦長之后,水膜厚度迅速增大,并在靠近葉頂和葉根的區域形成了兩個水膜聚集區,這兩個區域水膜的厚度均達到了90 μm以上。

圖8 葉片表面水膜厚度的分布

葉片表面水膜厚度的分布與相間剪切力、水膜黏性力、表面曲率、表面張力和壁面剪切力作用下葉片表面的水膜流動行為有關。圖9給出了葉片表面的水膜流速分布。與水膜厚度分布相對應,壓力面水膜流速在80%葉高以下沿徑向基本均勻,但在80%葉高以上沿徑向出現波動。在吸力面,葉根和葉頂兩個角區水膜出現低速區,其他區域的水膜速度梯度與流向大體相向。

圖9 葉片表面水膜速度的分布

葉片表面水膜厚度和速度的上述特征與葉柵通道內的二次流動密切相關。圖10給出了葉柵通道內及尾跡區二次渦的發展過程,其中c為軸向弦長,x為以進氣邊為原點的軸向坐標。結合圖8～圖10可以看到,在吸力面與上端壁形成的角區附近,主流通道渦和角渦所誘導的徑向速度通過相間剪切力帶動葉頂區域的水膜向葉展中部遷移,形成了吸力面頂部區域的水膜分布特征。造成吸力面葉根角區以及壓力面水膜沿葉高分布特征的原因與此類似。

圖10 葉柵通道中二次渦的發展過程

圖11給出了上端壁的水膜厚度和速度的分布。圖11a中:在葉片前緣?、?處,子午型線突然擴張使得上端壁邊界層區域的氣流產生分離,形成回流區,上端壁表面的水膜在氣流的剪切作用下產生堆積;由?和?區域水膜的流線分布可以觀察到,上端壁處水膜從壓力面向吸力面遷移,這使得上端壁表面靠近吸力面的水膜不斷增厚,形成水膜的帶狀聚積。根據連續性方程,帶狀聚積區水膜流量的增大也使得此區域的水膜流速明顯增加,如圖11b所示。

(a)水膜厚度(b)水膜速度 圖11 上端壁表面水膜特性參數的分布

在上端壁靠近葉片尾緣處,來自吸力面和壓力面的主氣流以及水膜均各自交匯并相互影響。主氣流流經葉片尾緣時形成低速的尾跡區,導致上端壁圖11a中 ?區的水膜速度比較低;在尾緣下游壓力面和吸力面氣流的壓差作用下,上端壁表面尾緣下游的水膜向吸力面偏移。圖11a中 ?區和 ?區的水膜聚積是主流通道渦在尾跡區遷移引起的,如圖12所示。通道渦在葉柵出口下游截面得到擴展,并導致上端壁表面的水膜厚度重新分布。

(a)x/c=1.55 (b)x/c=1.6 (c)x/c=1.8圖12 葉柵下游二次渦的發展過程

總的來看,影響水膜分布的主要因素有3點:一是壁面曲率,它通過影響壁面壓力分布改變了主流場的速度分布,速度分布又進一步影響相間的剪切力分布,從而影響表面水膜的速度和厚度分布;二是端壁表面附近橫向二次流對水膜的遷移作用,引起端壁表面水膜向葉片吸力面側聚積;三是通道渦和角渦的影響,引起水膜沿葉高重新分布。

3.2 水膜對葉柵流場的影響

葉片和端壁表面的水膜與主流相互作用,對葉柵的氣動特性產生了影響。圖13給出了85%～95%葉高處葉片表面壓力的分布。可以看到,在吸力面靠近尾緣區域,沿相對葉高方向水膜引起的表面壓力差異越來越明顯,在95%葉高處表面壓力變化幅值達到±300 Pa,約為該截面進、出口壓降的13%。該位置對應圖8中吸力面水膜聚積的區域。可以看到,吸力面靠近葉頂區域的水膜聚積是由角區氣流的二次流引起的,而水膜的聚積又反過來對葉柵中的流動產生了影響。

圖13 85%～95%葉高處葉片表面壓力分布

水膜的存在也使得葉片的出口氣流角發生了變化。如圖14所示,與無水膜時相比,進口氣流角相同,而水膜使葉柵的出口氣流角有所增加,在約85%葉高處增加了0.6°。

圖14 進、出口氣流角沿葉高的分布

對于本文分析的透平靜葉,由于水膜引起的氣流特性變化僅存在于局部區域,因此對葉柵的氣動特性沒有實質性改變。但是,考慮到透平葉片較厚,而水膜的厚度僅在數十微米量級,因此水膜引起葉片表面壓力和出口氣流角的變化相當顯著。對于航空發動機吸雨的情況,壓氣機葉片要薄得多,水膜對葉柵氣動特性可能產生更為顯著的影響。

4 結 論

本文對平板表面和透平靜葉中氣流和水膜的耦合作用進行了研究,主要結論如下。

(1)平板表面水膜厚度與進口水膜雷諾數呈1/2指數冪關系,與來流馬赫數呈反比關系,與出口背壓呈弱負指數次冪關系。水膜平均流速隨來流馬赫數的增加線性增大,與進口水膜雷諾數呈1/2指數冪關系,并隨出口背壓的增加逐步增大,但增速逐漸降低。直通道總壓損失系數比隨來流馬赫數、水膜流量的增大而增大,水膜附加損失對水膜流量和出口背壓的變化較為敏感。

(2)葉柵通道中影響壁面水膜分布的機理為:壁面曲率通過影響相間剪切力來影響水膜的厚度和速度;端壁上從壓力面到吸力面的橫向二次流引起水膜在吸力面附近聚積;通道渦和角渦引起水膜沿葉高重新分布。葉柵通道中水膜對氣流產生影響。沿葉高水膜聚集區的葉片表面壓力分布發生顯著變化,葉柵出口氣流角增加。

[1] NIKOLAIDIS T, PILIDIS P. The effect of water ingestion on an axial flow compressor performance [J]. Journal of Aerospace Engineering, 2014, 228(3): 411-423.

[2] BHARGAVE R, MEHERHOMJI C, CHAKER C, et al. Gas turbine fogging technology: a state-of-the-art review part I Inlet evaporative fogging analytical and experimental aspects [J]. Journal of Engineering for Gas Turbines and Power, 2007, 129(2): 443-453.

[3] MOORE M J, SIEVERDING C H. Aerothermodynamic of low pressure steam turbines and condensers [M]. Carlsbad, USA: Hemisphere Publishing Corporation, 1986: 1-190.

[4] YOUNG J B, YAU K K. The inertial deposition of fog droplets on steam turbine blades [J]. ASME Journal of Turbomachinery, 1988, 110(2): 155-162.

[5] YAU K K, YOUNG J B. The deposition of fog droplets on steam turbine blades by turbulent diffusion [J]. ASME Journal of Turbomachinery, 1987, 109(3): 429-435.

[6] 劉波, 曹志鵬, 高嵩, 等. 來流含水對航空發動機風扇/壓氣機特性的影響 [J]. 航空動力學報, 2006, 20(6): 1041-1047. LIU Bo, CAO Zhipeng, GAO Song, et al. Influence of inlet water ingestion on aero-engine fan-compressor performance [J]. Journal of Aerospace Power, 2006, 20(6): 1041-1047.

[7] KIRILLOV I I, IABLONIK R M. Fundamentals of the theory of turbines operating on wet steam [M]. Washington, DC, USA: NASA, 1970: 1-36.

[8] WILLIAMS J, YOUNG J B. Movement of deposited water on turbomachinery rotor blade surfaces [J]. ASME Journal of Turbomachinery, 2007, 129(2): 394-403.

[9] FENDLER Y, DOREY J M, STANCIU M, et al. Developments for modeling of droplets deposition and liquid film flow in a throughflow code for steam turbines: GT2012-68968 [R]. New York, USA: ASME, 2012.

[10]HAMMITT F G. Liquid film and droplet stability consideration as applied to wet steam flow [J]. Forschung im Ingenieurwesen: A, 1981, 47(1): 1-14.

[11]SCHLICHTING H, GERSTEN K. Boundary-layer theory [M]. Heidelberg, Berlin: Springer-Verlag, 2003: 497-518.

[12]LI Liang, YANG Jiandao, YOU Wei, et al. Investigation of the vapour-liquid two-phase flow in the low-pressure cylinder of a 1 000 MW nuclear power steam turbine [J]. Proc IMechE: Part A Journal of Power and Energy, 2014, 228(2): 178-185.

(編輯 苗凌)

Numerical Investigation for Coupled Flow Behavior Between Gas Flow and Wall Film of Flat and Turbine Stator

FAN Xiaojun1,LI Liang1,LI Sen2,ZHANG Xiang2

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. AECC Commercial Aircraft Engine Co. Ltd., Shanghai 200241, China)

A numerical algorithm was employed to investigate the coupled flow behavior between gas flow and wall film. The air flow and wall film on a flat, and the water vapor flow and wall film in a turbine cascade were focused on. It is concluded that the film thickness is approximately proportional to the root of the inlet wall film Reynolds number, and inversely proportional to the mainstream flow Mach number. Film thickness and the outlet pressure have a weak negative exponential order relation, and the interface velocity is linearly related to the outlet pressure. The additional losses due to water film are sensitive to the change of water flow rate, but not sensitive to the flow Mach number. As for the turbine stator, the pressure surface film thickness is relative even, except that a film accumulation region appears at the tip corner region. In contrast, the suction side thickness changes obviously, and the film accumulation is observed at both the tip and root corner regions. The wall film distribution in a turbine cascade is affected by three factors. The wall curvature influences the film thickness and velocity by influencing the interphase shear force. The endwall secondary flow from the pressure side to the suction side leads to film accumulation near the suction surface. The radial pressure gradient caused by passage vortex and corner vortex results in film redistribution along the blade height. On the other hand, the film accumulation on the blade exerts a significant impact on the surface pressure and outlet flow angle.

gas flow; wall film; coupling flow behavior; numerical investigation

2016-05-23。 作者簡介:范小軍(1992—),男,碩士生;李亮(通信作者),男,副教授,博士生導師。

時間:2016-09-08

10.7652/xjtuxb201611002

TK263.3

A

0253-987X(2016)11-0007-07

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160908.1101.002.html