一種求解含圍帶阻尼成圈葉片振動響應的高效方法

邱恒斌,徐自力,劉雅琳,上官博

(1.西安交通大學機械結構強度與振動國家重點實驗室,710049,西安;2.西安建筑科技大學環境與市政工程學院,710055,西安;3.西安熱工研究院有限公司,710032,西安)

?

一種求解含圍帶阻尼成圈葉片振動響應的高效方法

邱恒斌1,徐自力1,劉雅琳2,上官博3

(1.西安交通大學機械結構強度與振動國家重點實驗室,710049,西安;2.西安建筑科技大學環境與市政工程學院,710055,西安;3.西安熱工研究院有限公司,710032,西安)

針對含圍帶阻尼成圈葉片的非線性振動響應計算時自由度多、迭代求解計算量大的問題,綜合波傳動法、高階諧波平衡法及Receptance法推導了一種求解含圍帶阻尼成圈葉片振動響應的高效方法。根據成圈葉片結構周期對稱的特點,采用波傳動法,將含圍帶阻尼成圈葉片降階為一個基本扇區進行振動分析,接觸面的非線性摩擦力可由單個扇區的位移結合干摩擦模型求得;將降階后單個扇區的時域振動微分方程由高階諧波平衡法轉化為頻域代數方程,通過葉片正則振型的正交性對頻域的振動方程進行解耦,并利用葉片局部非線性的特點對非接觸面上的線性自由度進一步縮聚,從而減少非線性迭代的規模,提高計算效率。算例結果表明:采用所提求解方法的響應計算結果與采用整體模型的結果相差小于0.33%,計算時間縮短為原來的10%,驗證了該方法的正確性、高效性,同時采用該方法研究了真實圍帶阻尼葉片的非線性振動響應。

成圈葉片;振動響應;圍帶阻尼;降階方法

為了避免透平機械發生高周疲勞,葉片系統經常采用干摩擦阻尼結構來增加阻尼以減小葉片的振動幅值[1-2]。葉片振動過程中,干摩擦阻尼結構利用接觸面之間振動產生的相互摩擦來消耗振動能量,降低振動水平。干摩擦阻尼結構的存在使葉片系統成為變剛度、變阻尼的非線性動力學系統。為了更好研究干摩擦阻尼結構葉片的振動特性,葉片系統常采用有限元模型進行分析。由于葉片系統的響應求解是一個非線性迭代過程,成圈葉片有限元模型自由度過多將導致迭代求解計算量非常大,直接求解難以實現。

本文綜合波傳動法、高階諧波平衡法及Receptance法發展了一種計算圍帶成圈葉片非線性振動響應的高效求解方法,給出了該求解方法的詳細推導過程。

1 求解方法

1.1 基于波傳動法的圍帶成圈葉片降階

當葉片靜止時相鄰葉片圍帶之間存在間隙,工作時葉片在離心力的作用下發生反向扭轉變形,這種扭轉變形使相鄰葉片圍帶相互接觸形成摩擦接觸面。葉片振動時,圍帶接觸面相互摩擦產生摩擦力消耗振動能量,減小振動幅值。當每只葉片受相同幅值、不同固定相位的氣流激勵時,相鄰葉片各點的位移幅值相同且存在一個固定相位差。在該氣流激勵下采用波傳動法,將具有循環對稱特性的成圈葉片降階成一個基本扇區的模型進行分析,相鄰基本扇區之間的耦合力通過施加周期對稱邊界條件實現,可得整圈葉片的動力特性。

單個葉盤扇區有限元模型如圖1所示,其有限元振動方程為

fb(qb(t))

(1)

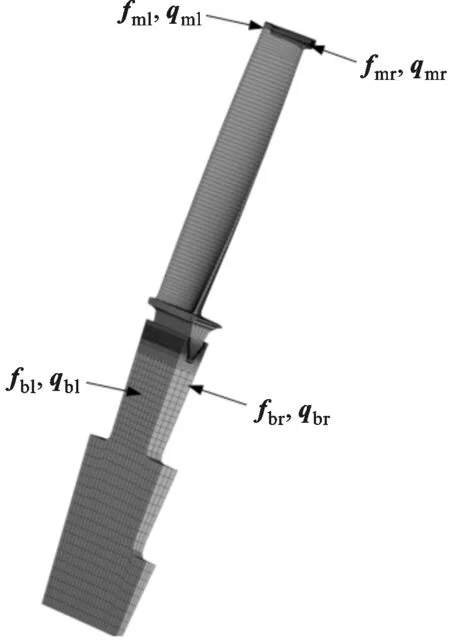
圖1 單個扇區的有限元模型

基本扇區的振動位移向量、摩擦力、周期對稱面耦合力按左右摩擦接觸面和周期界面自由度進行分塊,即

(2)

(3)

(4)

式中:qml(t)、qmr(t)為左、右接觸界面節點的位移;qbl(t)、qbr(t)為左、右周期對稱面節點的振動位移;qo(t)為基本扇區其他節點的位移;fml(t)、fmr(t)為左、右接觸面節點摩擦力;fbl(t)、fbr(t)為左、右周期對稱界面的耦合力。

根據波傳動法[7],左右周期對稱界面上節點的振動位移和耦合力的關系為

qbr(t)=e-ihφI·qbl(t)

(5)

fbr(t)=-e-ihφI·fbl(t)

(6)

式中:I為單位矩陣;h為激勵的階數;φ=2π/N為相鄰扇區之間的振動相位角;N為葉片數。

由式(5),可對基本扇區的振動位移q(t)進行縮減處理,即

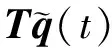
(7)

將式(7)代入式(1),并做變換,則基本扇區的振動方程變為

(8)

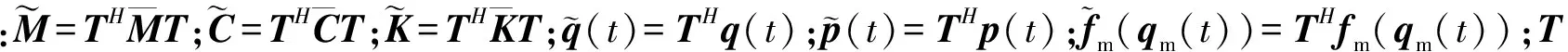
因此,通過波傳動法施加周期邊界條件,在變換過程中左周期對稱界面上的自由度減小,且消去了未知周期對稱界面上的耦合力。

根據周期對稱結構的特點,對于第j、j+1個葉盤扇區,摩擦接觸面上的振動位移關系為

qj+1(t)=qj(t+δt)=e-ihφqj(t)

(9)

第j個葉片左接觸面和第j-1個葉片右接觸面的相對位移及第j個葉片右接觸面和第j+1個葉片左接觸面的相對位移為

(10)

(11)

左右接觸面上的相對位移存在關系

(12)

接觸點對的非線性干摩擦力由相鄰葉片接觸面間的相對位移結合三維干摩擦微滑移模型[10]確定。同時,由于接觸面振動位移是周期性的,故接觸面的相對位移和干摩擦力也是周期性的。

1.2 振動響應的求解

諧波平衡法是求解非線性問題有效、快速的方法。葉片振動時接觸面會有黏滯、滑移、分離的運動狀態,分離時非線性項中的高次諧波對振動影響很大,對一次諧波平衡法的計算結果產生較大誤差[2],因此本文采用高階諧波平衡法求解振動方程。

當干摩擦阻尼葉盤系統受到周期性氣流激勵作用時,假設其振動響應與界面約束力均呈現周期性變化,可將葉盤系統的振動響應、氣流激振力和干摩擦力展開成傅里葉級數

(13)

(14)

(15)

式中:h為諧波階數;H為諧波平衡法中考慮的最大諧波數;ω為氣流激振力的基頻;Qh、Ph和Fmh分別為振動響應、激振力和接觸面摩擦力的第h階諧波的系數。

將式(13)～(15)代入式(8),可得非線性代數方程組

(16)

式(16)在頻域內計算葉片的響應時,僅通過單個扇區的位移信息計算接觸面的摩擦力,通過反復迭代計算得到系統的穩態響應。

盡管采用波傳動法對成圈葉片進行了降階,但由于葉片結構復雜,單只葉片有限元模型中通常有上萬個節點,因此方程個數非常多,迭代求解很耗時,需要進一步降階。本文將采用Receptance法做降階處理,以便高效快速地求解葉片系統的非線性振動響應。Receptance法利用葉片正則振型的正交性對葉盤系統的振動方程進行解耦,然后利用葉盤系統接觸界面非線性自由度遠小于總體自由度的特性,只需要迭代求解葉盤系統接觸界面上非線性自由度的振動響應,其余自由度上的振動響應可直接求解,從而可顯著提高計算效率。

根據Receptance法,式(16)可寫為

(17)

(18)

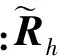
一般情況下,系統的前幾階振型對振動響應貢獻較大,因此在計算過程中忽略系統的高階振型,只考慮前幾階振型,式(18)可改寫為

(19)

式中:M為計算過程振型的最高階數。

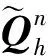
(20)

(21)

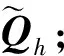
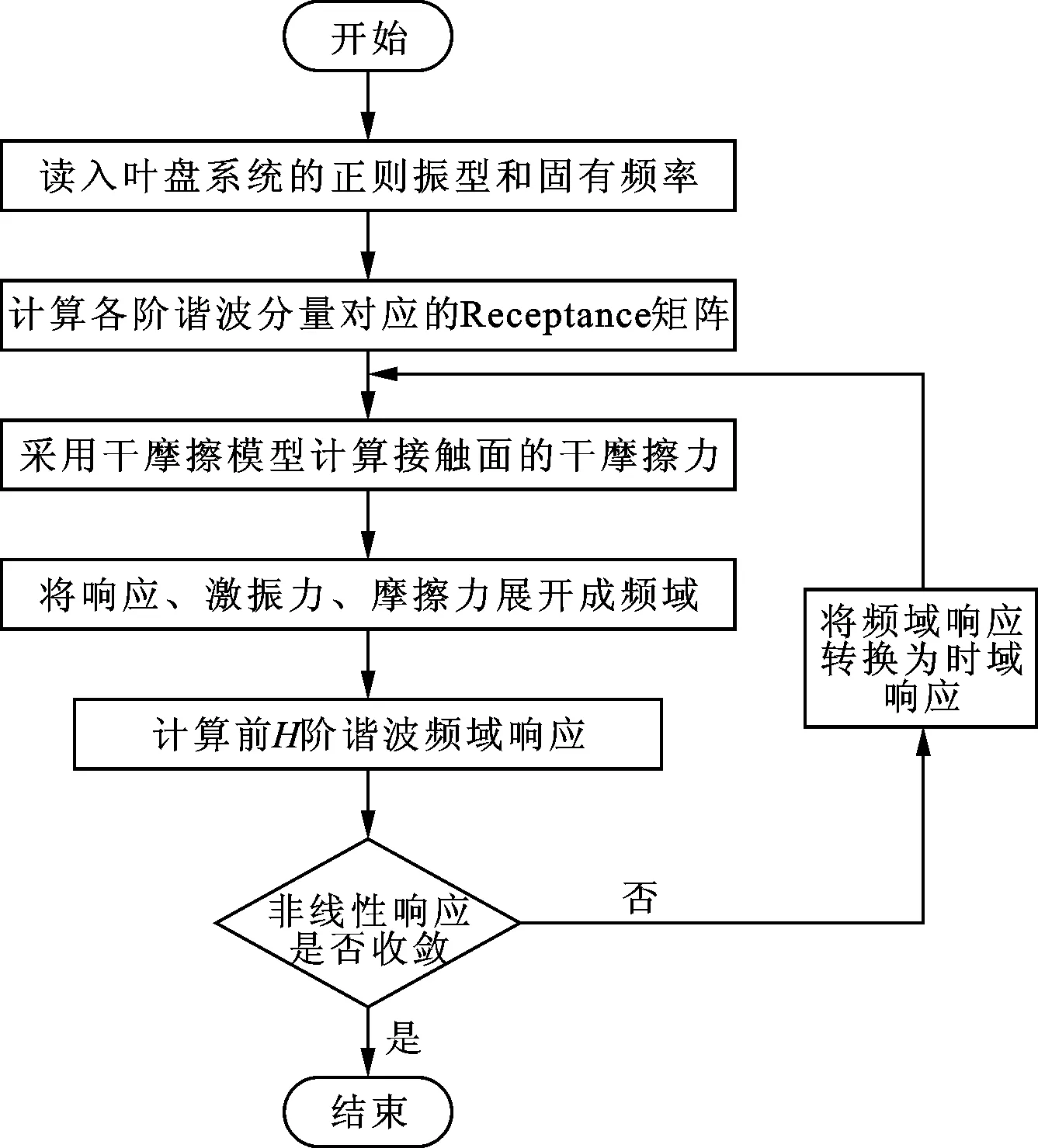
圖2 計算摩擦接觸面自由度振動響應的流程圖

2 數值算例分析

2.1 計算方法的驗證

為了驗證本文方法的準確性和高效性,本文采用該降階方法計算某簡化圍帶成圈葉片的非線性振動響應,并與整體模型的直接計算結果進行比較。

簡化的圍帶葉片扇區和成圈葉片整體結構的有限元模型如圖3所示。葉片采用六面體八節點單元劃分,成圈葉片由30個葉片組成,單個扇區包含3 240個節點,整體結構包含91 320個節點。材料參數為:密度ρ=7 800 kg/m3,彈性模量E=200 GPa,泊松比υ=0.3。

(a)單個扇區 (b)整體結構圖3 簡化的葉片模型

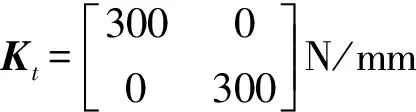
在葉片系統第一階固有頻率附近,取葉頂某一點的x、y、z方向的總位移,采用降階方法和整體模型的計算結果如圖4所示。

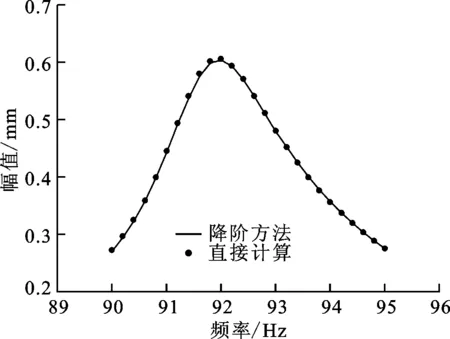
圖4 降階方法和直接計算結果

由圖4可看出,采用降階方法和整體模型計算得到的結果吻合得很好,最大相對誤差位于共振點附近,直接計算的響應結果為0.607mm,降階方法計算的結果為0.605mm,兩者相差0.33%,計算時間僅為原來的10%。計算結果表明了本文降階方法的正確性和高效性。

2.2 真實圍帶葉片分析

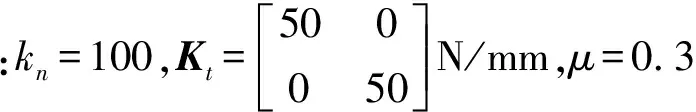
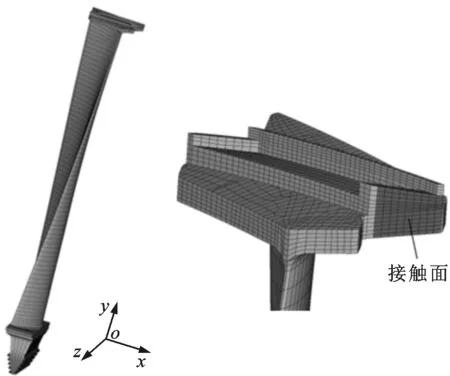
圖5 真實圍帶葉片有限元模型

圍帶葉片在安裝時存在一定的初始間隙,機組啟動時,葉片在扭轉恢復力的作用下初始間隙會逐漸減小,使圍帶之間形成摩擦接觸面,并影響接觸面的初始正壓力,不同的初始間隙對應不同的初始正壓力。本文計算中初始正壓力的取值是根據扭轉恢復后圍帶平均接觸應力和平均接觸面積計算得到的,本文通過計算圍帶葉片在不同初始正壓力的振動響應,分析初始安裝條件對圍帶葉片減振效果的影響,不同初始正壓力下葉片系統的幅頻響應曲線如圖6所示。

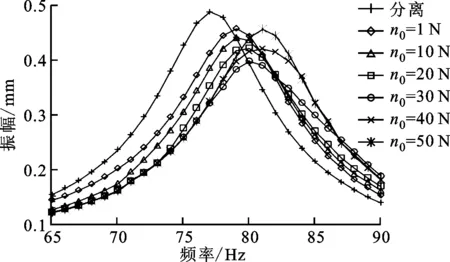
圖6 不同初始正壓力的幅頻響應曲線

由圖6可看出,圍帶葉片的響應沒有出現多值、跳躍等典型的非線性特征,這是因為實際葉片設計時初始正壓力比較大,在振動過程表現出的是弱非線性行為。共振幅值與初始正壓力的關系和共振頻率與初始正壓力的關系如圖7、8所示。

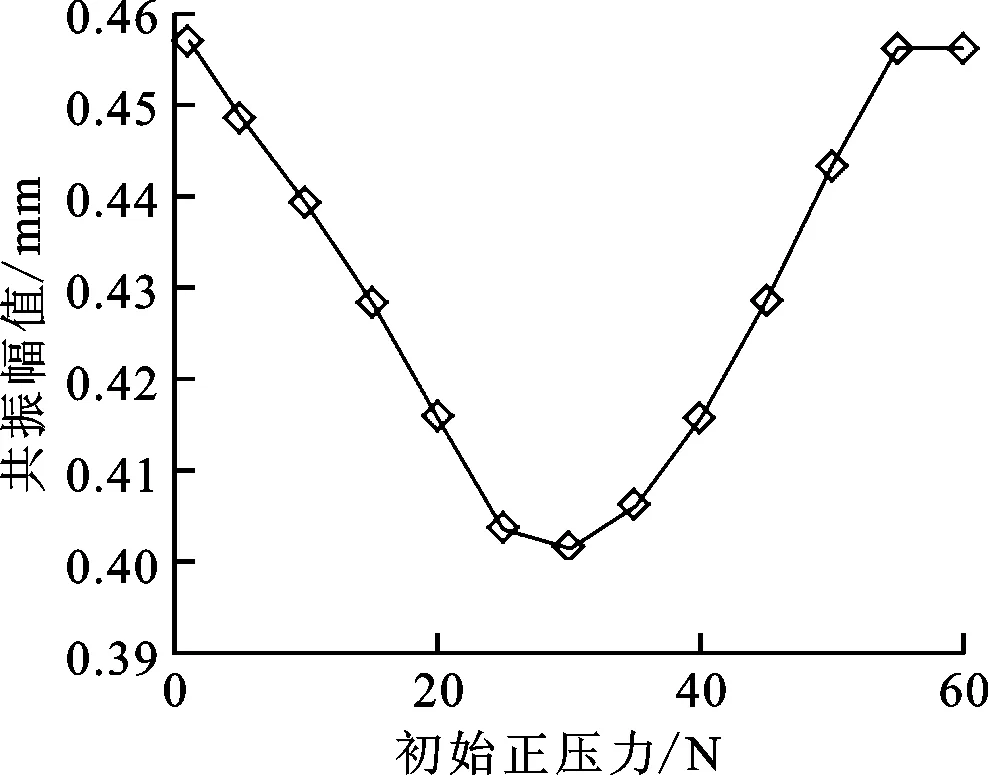
圖7 共振幅值與初始正壓力的關系

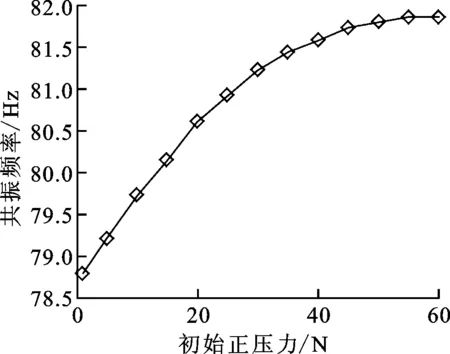
圖8 共振頻率與初始正壓力的關系

由圖7、8可看出,當接觸面存在初始正壓力時,隨著初始正壓力的增加,葉片共振峰值先減小后增大,最后趨于穩定,存在一個最優的初始正壓力使葉片的共振幅值最小;共振頻率隨著正壓力的增加而增加,最終趨于兩接觸面為接觸剛度連接時葉片的固有頻率。這是因為當圍帶接觸面間的初始正壓力較小時,圍帶間振動產生的摩擦力較小,此時摩擦力耗能小;隨著初始正壓力的增大,圍帶間的摩擦力逐漸增大,減振效果變好;當接觸面初始正壓力大到一定程度后,圍帶間難以產生相對運動,摩擦力耗能減小,減振效果變差。共振頻率不斷增大是因為初始正壓力的增加使相鄰圍帶間的相互約束逐漸變大。

3 結 論

本文綜合波傳動法、高階諧波平衡法及Receptance法推導了一種計算圍帶成圈葉片的非線性振動響應的高效求解方法。該方法利用葉片系統的周期對稱性,采用波傳動法將成圈葉片降階為一個基本扇區進行分析,使求解規模大幅度降低。該方法考慮了高次諧波的影響,能夠求解復雜周期激勵下葉片系統的非線性響應。通過葉片模態的正交性對葉盤系統的振動方程進行解耦,并利用葉片系統局部非線性的特點對非接觸界面上的線性自由度進一步縮聚,從而減少了非線性迭代的規模,提高了計算效率。

采用本文求解方法得到的計算結果與采用整體模型的結果進行比較,結果驗證了該方法的正確性與高效性。采用該方法預測了某真實圍帶葉片的振動響應,研究了初始正壓力對圍帶葉片減振效果的影響,結果表明存在一個最優的初始正壓力使葉片共振幅值最小,圍帶接觸面間的初始正壓力可通過調整葉片安裝時的圍帶間隙來實現。

[1] 谷偉偉, 徐自力. 干摩擦阻尼葉片的界面約束力描述及振動響應求解 [J]. 振動工程學報, 2012, 25(1): 64-67. GU Weiwei, XU Zili. Description of constraint force for dry friction and prediction of vibration responses on damped blade [J]. Journal of Vibration Engineering, 2012, 25(1): 64-67.

[2] 史亞杰, 單穎春, 朱梓根. 帶凸肩葉片非線性振動響應分析 [J]. 航空動力學報, 2009, 24(5): 1158-1165. SHI Yajie, SHAN Yingchun, ZHU Zigen. Analysis of nonlinear response of shrouded blades system [J]. Journal of Aerospace Power, 2009, 24(5): 1158-1165.

[3] PANNING L, SEXTRO W, POPP K. Optimization of the contact geometry between turbine blades and underplatform dampers with respect to friction damping [C] ∥Proceedings of ASME Turbo Expo 2010: Power for Land, Sea and Air. New York, USA: ASME, 2002: 991-1007.

[4] KURAN B, ?ZGüVEN H N. A modal superposition method for non-linear structures [J]. Journal of Sound and Vibration, 1996, 189(3): 315-339.

[6] PETROV E P. A method for use of cyclic symmetry properties in analysis of nonlinear multiharmonic vibrations of bladed disks [J]. ASME Journal of Turbomachinery, 2004, 126(1): 175-183.

[7] THOMAS D L. Dynamics of rotationally periodic structures [J]. International Journal for Numerical Methods in Engineering, 1979, 14(1): 81-102.

[8] 謝永慧, 張荻. 汽輪機阻尼圍帶長葉片振動特性研究 [J]. 中國電機工程學報, 2005, 25(18): 96-90. XIE Yonghui, ZHANG Di. Numerical model for vibration characteristic of steam turbine blade with damped shroud [J]. Proceedings of the CSEE, 2005, 25(18): 96-90.

[9] 秦飛, 張曉峰, 白潔, 等. 循環對稱結構動應力計算的一種工程處理方法 [J]. 北京工業大學學報, 2006, 32(s1): 64-67. QIN Fei, ZHANG Xiaofeng, BAI Jie, et al. A new approach of dynamic stress analysis for cyclic symmetry structures [J]. Journal of Beijing University of Technology, 2006, 32(s1): 64-67.

[10]GU W W, XU Z L. 3D numerical friction contact model and its application on nonlinear vibration of damping blade [C] ∥Proceedings of ASME Turbo Expo 2010: Power for Land, Sea and Air. New York, USA: ASME, 2010: 809-817.

(編輯 趙煒 苗凌)

An Efficient Method for Solving Vibration Response of Continuous Covered Blades with Damped Shroud

QIU Hengbin,XU Zili,LIU Yalin,SHANG GUAN Bo

(1. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China; 2. Institute of Environmental and Municipal Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China; 3. Xi’an Thermal Power Research Institute Co. Ltd., Xi’an 710032, China)

An efficient solution method based on wave propagation method, multi-harmonic balance method and Receptance method was developed to solve the problem with overlarge degrees of freedom and computational complexity in calculating the nonlinear vibration response of continuous covered blades with damped shroud. According to the cyclic symmetry property of blade, the vibration analysis of a whole blade can be reduced to one of its basic sector using wave propagation method and the nonlinear friction force can be solved from the displacement of the basic sector and friction contact model; the differential equations in time domain of the reduced basic sector can be transformed into algebraic equations in frequency domain by multi-harmonic balance method. The orthogonality of normalized modes is used to decouple the vibration equation of blade in frequency domain and the local nonlinear characteristics of the blade system are used to condense the linear DOFs in non-contact interfaces. So that the scale of nonlinear iteration can be effectively reduced and the computation efficiency is improved. The results showed that the relative error obtained with the developed method was 0.33% and the calculation time was reduced to 10%, which verifies the accuracy and efficiency of the proposed method. The nonlinear vibration response of a real shrouded blade was investigated by this method.

whole blade; vibration response; shroud damper; order-reducing method

2016-04-07。 作者簡介:邱恒斌(1991—),男,碩士生;徐自力(通信作者),男,教授。 基金項目:國家自然科學基金資助項目(51275385)。

時間:2016-09-14

10.7652/xjtuxb201611001

TK263.3

A

0253-987X(2016)11-0001-06

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160914.1805.008.html