求解多目標柔性作業車間調度問題的兩階段混合Pareto蟻群算法

趙博選,高建民,陳琨

(西安交通大學機械工程學院,710049,西安)

?

求解多目標柔性作業車間調度問題的兩階段混合Pareto蟻群算法

趙博選,高建民,陳琨

(西安交通大學機械工程學院,710049,西安)

針對多目標柔性作業車間調度問題(FJSP)分解得到的作業分派、排序子問題仍是多目標優化問題的情況,提出了一種求解該問題的分層Pareto優化框架,并采用該框架構建了兩階段混合Pareto蟻群算法的求解算法,其中兩個Pareto蟻群系統分別求解多目標作業分派、排序問題。結合GT算法、排產規則評估和過濾第一階段的分派方案,將具有較好評估全局解的分派方案作為分派階段的精英檔案,并輸入給排序蟻群系統獲取其非支配調度解,進而獲取問題全局非支配解。子問題算法混合了各目標相關的鄰域搜索策略,與Pareto蟻群算法結合,以期提高解的質量。通過求解帶有平均工件加權延遲時間指標的多個FJSP基準算例,驗證了算法的有效性。計算結果表明,該分層Pareto優化框架對原問題進行分層分解,有利于降低原問題的復雜性,相比多數文獻,算法能夠獲得各基準算例Pareto非支配解,從而為分解求解復雜多目標調度優化問題提供了一種途徑。

多目標柔性作業車間調度;分層Pareto優化;兩階段Pareto蟻群算法;鄰域搜索

柔性作業車間調度問題(FJSP)是傳統作業車間調度問題的擴展。在柔性作業車間調度問題中,每道工序的加工設備是不確定的。工件可以在多個可選擇設備上加工,采用不同加工設備所需加工時間不同,且工件可能重復訪問同一設備,設備不確定性和可重復訪問性增加了FJSP調度優化的復雜性,使FJSP成為更加復雜的NP-hard問題。FJSP包含作業分派(OA)與排序(OS)兩部分內容,其求解方法可分為集成求解和分層求解,集成求解同時考慮OA與OS的優化[1-4],分層求解根據兩子問題的繼承性分階段優化,進而得到問題全局解,降低了問題復雜性[5-7]。

多目標FJSP求解方法分為加權和優化及Pareto優化兩類。加權和優化采用已知權重將多目標優化轉化為單目標優化[6-8],Pareto優化基于Pareto最優的思想獲取問題解空間多樣化、近優性的非支配前沿[9-10]。加權和優化可在各目標權重已知的情況快速得到問題部分解,但大多數車間生產內外部環境動態變化,Pareto優化為生產管理者提供數量較多的調度方案以供決策。

按照問題分解求解的思想,原問題被分解之后,子問題圍繞與之相關的目標子集優化。例如,多目標FJSP分解之后的OA子問題根據問題本身性質,其目標子集包含總負荷與負荷均衡度等相關指標,而OS子問題目標子集包含完工周期與交付性相關指標,故多目標FJSP分解之后得到兩個多目標優化子問題。當分層求解方法面對兩階段均屬于多目標優化問題時,除構建子問題求解算法外,如何選取前者解集進入后者求解算法是該問題的關鍵。分層加權和求解方法可采用加權和方式對前者結果進行評估,選擇最優結果進入后者,但分層Pareto求解方法卻不能簡單將前者非支配解集提交給后者求解算法。

本文結合分層求解和Pareto優化方法,研究求解多目標FJSP的分層Pareto求解方法,構建兩階段混合Pareto蟻群算法求解柔性作業車間調度問題。Pareto蟻群算法混合各目標相關的鄰域搜索算法,實現二者協同進化。

1 FJSP描述

記J={Ji,1≤i≤n}為調度工件集合,工件序號為i;每個工件Ji包含ni道工序,工序順序預先確定,工件Ji的第j道工序可以表示為Oij;工件具有不同的權重系數ωi和交貨期di。記M={Mk,1≤k≤m}為加工設備集合,設備序號為k;可以加工工序Oij的設備集合為Mij?M,工序Oij在Mk上加工,不可中斷,且加工時間為tijk。

要求為每個工件的工序選擇合適的加工設備并確定各設備上的工序加工順序及開始加工時間,同時滿足各工件的加工工藝等約束條件,實現多個調度性能指標最優。

考慮最大完工時間最小、總負荷最小、最大設備負荷最小和平均工件加權延遲時間最小4種性能指標,即

(1)

(2)

(3)

(4)

決策變量

(5)

(6)

約束條件

(7)

?1≤i≤n, 1≤j≤ni, 1≤i′≤n, 1≤j′≤n,

(8)

(9)

(10)

2 一種兩階段Pareto優化算法框架

由于設備的非等效性、工藝的多樣性以及設備可重入性,FJSP分解之后的OA與OS子問題兩者解空間的非支配性不具備繼承性,即OA子問題的非支配前沿分派解經過OS子問題優化后不一定是OS子問題的非支配前沿調度解,且OS子問題的非支配前沿調度解不一定是由OA子問題的非支配前沿分派解得來,所以不能簡單保留OA子問題的非支配前沿解作為第1階段的優化結果。分層求解方法需要對前者子問題的求解結果進行評估和優選,一方面盡可能過濾較差分派解進入第2階段,另一方面不能丟失問題最優解對應的分派解。采用啟發式規則排產算法快速構建分派方案的優秀調度解,得到分派解的全局目標值參與評估和優選,最終選擇評估后具有較優全局目標值的分派解作為第1階段的優化結果。

通過大量仿真實驗提出分層Pareto優化算法框架前,總結2個改進措施:①子問題1優化一定次數后,使其較優解處于較穩定時才進行評估和優選,有利于降低評估與優選操作運行次數,根據非支配關系,子問題1的非支配解集一定是問題全局解(所有目標集合)的非支配解集;②評估和優選之后的較優解暫時保留在第1階段精英檔案中,每次評估和優選之后更新該精英檔案,等第1階段優化完畢后,將該精英檔案輸出給第2階段進行搜索。這樣可大量過濾算法運行過程中的較差分派解,且將兩子問題之間的嵌套關系改成并列關系,有利于減少算法運行時間。求解多目標FJSP的分層Pareto優化算法框架如圖1所示。

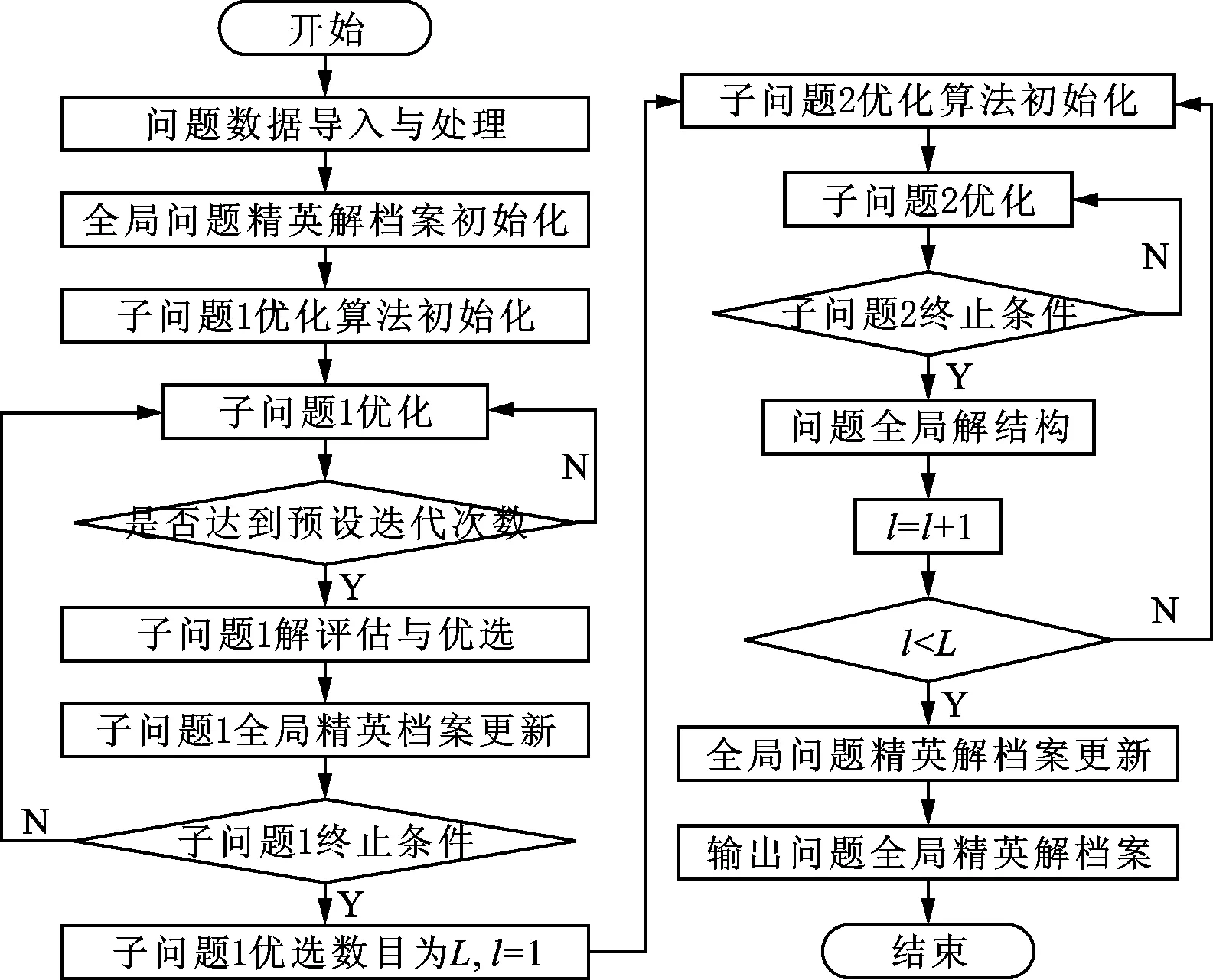
圖1 分層Pareto優化算法框架

3 兩階段混合Pareto蟻群算法

3.1 FJSP析取圖描述

為了應用蟻群算法,FJSP問題用析取圖表示為D=(O,A,B),其中O為節點集合,A為連接弧集合,B為析取弧集合。開始節點OS和結束節點OE分別用于連接各工件的首尾工序;有向弧表示各工件的工藝路線,連接具有順序約束的工序節點;析取弧表示不同工件之間可能工序的順序關系,以待確定;同一工序的不同可選設備節點之間不存在析取弧。與JSSP問題不同的是,該析取圖將可選設備添加在工序節點中,且不是所有的節點都要被遍歷,調度結果只是所有節點的部分連接圖。同一工序的設備節點具有互斥關系,當某工序節點的加工設備確定,該工序的其他設備節點即被舍棄。每個節點被表述為(Oi,j,Mk),表示工件的第j道工序在設備k上加工,4個工件的析取圖描述如圖2所示。多目標蟻群算法會得到多個加工路徑,這些加工路徑對應的解在解空間具有非支配性。

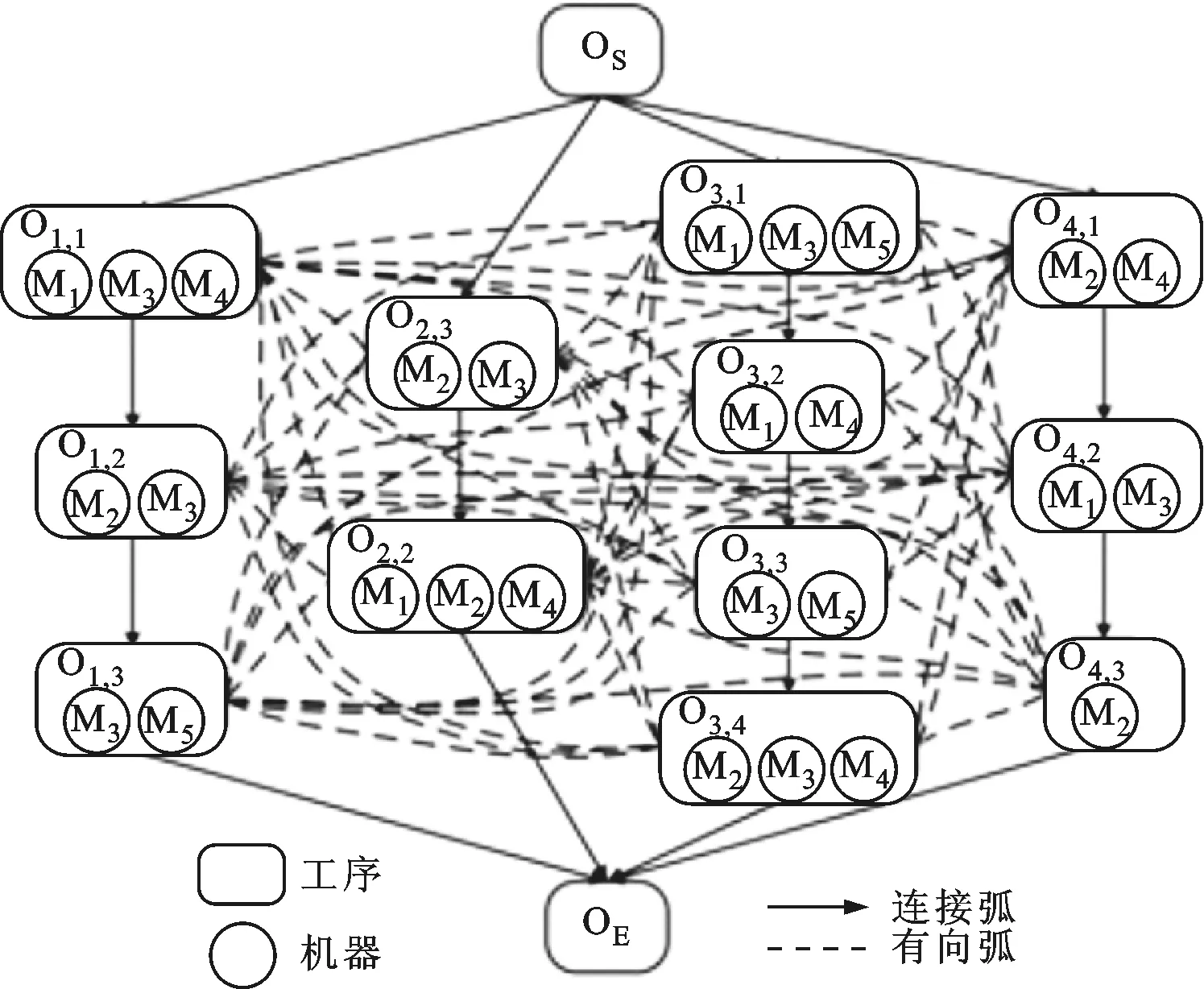
圖2 FJSP問題析取圖描述示例

3.2 兩階段混合Pareto蟻群系統構建

詳細的Pareto蟻群算法關鍵操作可參考文獻[11-12]。OA蟻群系統根據信息素與啟發式信息確定各工序操作的加工設備,每只螞蟻遍歷路徑前隨機排列所有工序,并保證工藝可行性,如圖3所示。

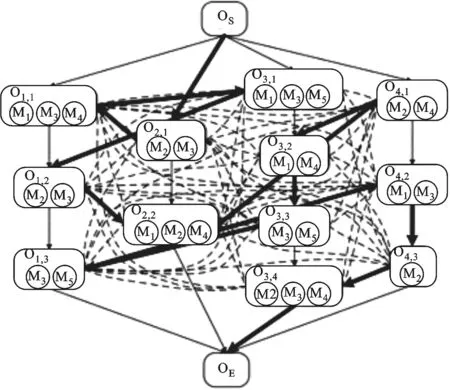
圖3 父代蟻群系統搜索示例

給定x為工序總數,y為設備總數,信息素矩陣構建為[τv,k]x×y,工序設備節點總負荷相關啟發式信息為其加工時間的倒數,工序設備節點負荷偏差相關啟發式信息為該設備已分配負荷的倒數。為使分母不為0,預先給每個設備預設合適的已分配負荷初始值。

圖5 基于關鍵路徑及公共關鍵塊的完工周期相關鄰域搜索操作示意圖

如圖4所示,OS蟻群系統通過遍歷所有工序操作節點來構建分派方案調度解,考慮到優化目標的正則性,本文結合GT算法[10]來縮小搜索范圍,減少算法搜索時間。具體流程為:①添加各工件首工序至可選工序任務集合,并計算集合中各工序操作最早可能開工與完工時間;②找出任務集合中工序操作最早可能完工時間和分派設備;③找出任務集合中分派在設備上最早可能開工時間小于完工時間的工序操作,形成沖突工序操作集合;④根據蟻群啟發式策略從操作集合中選擇一個工序安排,從任務集合中剔除該工序,如果該工序不是工件末工序,添加其下一工序操作至任務集合;⑤更新任務集合中受影響工序操作最早可能開工與完工時間,如果任務集合為空,停止,否則返回至流程②。

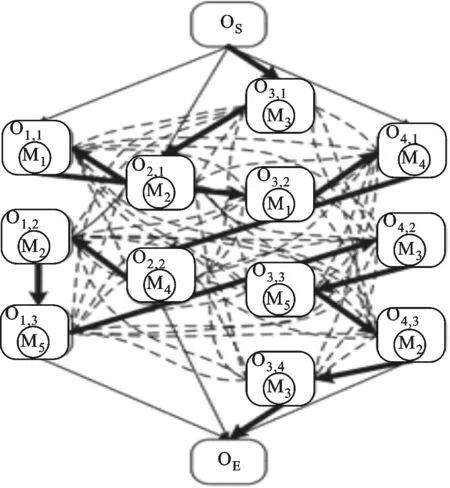
圖4 OS蟻群系統搜索示例

完工周期相關啟發式信息為該弧段后工序任務加工時間的倒數;交付性相關啟發式信息為該弧段后工序任務分解交付期的倒數。計算各工件工序操作的分解交付期,即

(11)

3.3 鄰域搜索策略

單目標優化問題中,當鄰域搜索解較優時代替初始解,而在多目標優化問題中,若鄰域搜索得到的解與原先解比較具有非支配性時,將該鄰域搜索解保存于緩沖池中。當所有鄰域搜索執行完畢后,從緩沖池取出非支配解,更新原始檔案。由于各目標的互斥性,本文提出與各目標相關的鄰域搜索策略,每次鄰域搜索以期某個目標相比之前更優,鄰域搜索策略如下。

(1)總負荷目標相關的鄰域搜索。找到分派工序數目最多的設備,隨機選擇該設備上某一工序,改派至其他較小加工時間可選設備上。

(2)最大設備負荷目標相關的鄰域搜索。按照已分派負荷對設備排序,隨機選擇最大負荷設備上工序操作分派在其他較小負荷可選設備上。

(3)完工周期目標相關的鄰域搜索。要想縮短完工周期,鄰域搜索只有通過移動關鍵路徑上的工序才可能減少最大完工時間,而當調度方案含有多條關鍵路徑時,只有基于公共關鍵塊的鄰域結構才會有助于縮短完工周期。本文基于公共關鍵塊采用以下鄰域結構:塊首工序插入到塊內工序之后;塊尾工序插入到塊內工序之前;塊內工序插入到塊首之前;塊內工序插入到塊內之后;塊首或塊尾兩工序交換。圖5歸納了基于關鍵路徑及公共關鍵塊的完工周期相關鄰域搜索策略所包含的操作。

(4)加權延遲時間相關鄰域搜索。文獻[4]介紹了一種交換式交付期相關鄰域搜索策略,先比較工件完工時間與交貨期,將其分為提前類和延遲類,逐個設備尋找相鄰工序滿足前工序屬于提前類、后工序屬于延遲類的兩相鄰工序,然后交換它們。

3.4 兩階段混合Pareto蟻群算法流程

在OA、OS Pareto蟻群系統中,每次迭代得到的所有螞蟻解經歷了新信息素矩陣和隨機權重的引導,新的螞蟻解對檔案的補充增加了檔案解的多樣性,而鄰域搜索可進一步提高解的質量。在OS蟻群系統中對精英檔案EA_OS進行鄰域搜索,而在OA蟻群系統中對所有螞蟻新解和精英檔案EA_OA進行鄰域搜索,用所有新解更新EA_OA和最優新分派解檔案Best_OA_New,Best_OA_New為多次迭代之后需要評估的分派解檔案。

本文采用算法迭代達到預定最大次數、非支配解集不再變化達到預定次數兩種算法為終止條件,算法詳細流程如圖6、7所示。

圖6 OA蟻群系統算法流程

3.5 OA分派解評估與優選

本文結合GT算法與多種排產規則為分派解構建可行調度方案,評估完工周期與平均加權延遲時間指標。排產規則包括隨機選擇規則,最早完工時間優先,最早操作分解交貨期優先,最多工作量剩余優先,最多操作數目剩余優先。按照事先設計好的概率分配,選取排產規則確定GT算法中沖突工序順序,得到該分派方案的調度解參與評估,當出現多種可選狀況時采用隨機選擇規則輔助選擇。對各個新分派解按照以上方法構建多個可行調度解(本文設定為30),與分派解子目標集聯合,并添加至分派解全局精英檔案gEA_OA,根據支配關系從gEA_OA中保留一定數量較優分派方案,實現gEA_OA檔案更新,在該檔案中一個分派解可能對應多個非支配全局精英解。

4 算例分析

為證實算法的有效性,本文應用該算法求解了帶有平均加權延遲時間指標的多組基準算例,分別為Kacem8×8算例、10×7算例、10×10算例和15×10算例,工件交付期信息如表1所示,其中時間為無量綱單位時間。算法參數:前3個算例螞蟻數目P=20,螞蟻信息素初值τ0=1;15×10算例螞蟻數目P=30,τ0=0.1,揮發系數ξ=0.1,全局釋放系數ρ=0.1,信息素權重因子α=1,啟發性知識權重因子β=1,偽隨機概率q0=0.6。仿真實驗表明,該參數組合能使兩階段Pareto蟻群算法在禁用鄰域搜索操作時得到較好質量的問題解集。

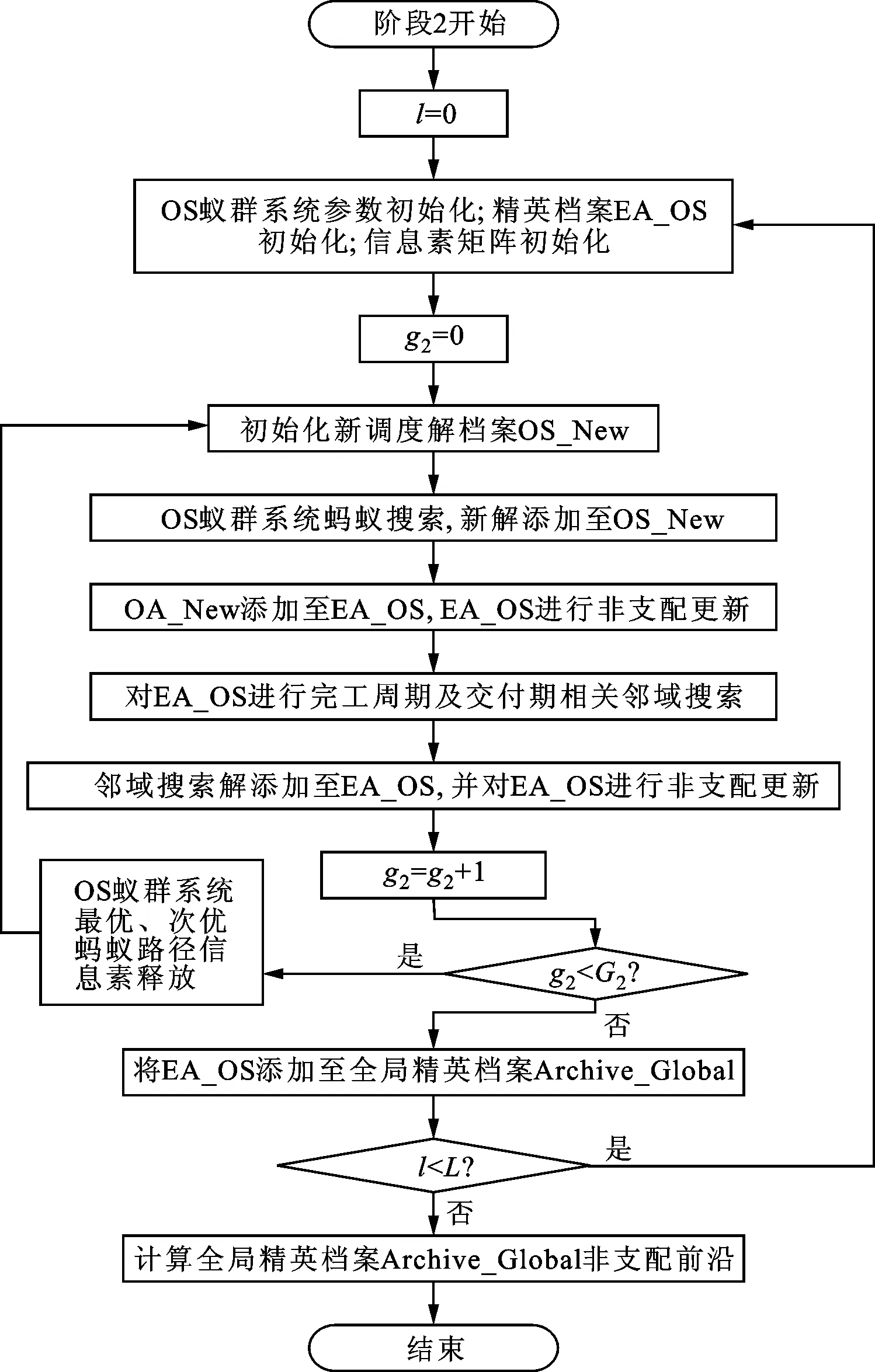
圖7 OS蟻群系統算法

分派階段的全局精英檔案gEA_OA的規模會影響算法整體運行時間。根據試驗數據,問題Pareto非支配前沿對應的分派解主要屬于分派解全局精英檔案gEA_OA的前幾個非支配等級,說明了評估和優選的有效性,根據該特征、結合問題規模,可控制該檔案的規模。本文前3個算例設置的gEA_OA檔案規模為30,15×10算例設置的gEA_OA檔案規模為40。按照以上設置,將算法運行10次,對各算例的運行時間(均值/方差)分別為152/28.3,162/23.7,168/31.2,445/34.8 s。編程語言為Matlab2010,運行環境為CPU i3-2120,主頻為-3.30～3.30 GHz,內存為4 GB。表2給出了附加平均工件加權延遲時間指標的Pareto最優解,粗體字符表示從文獻[3-4,6-10]獲取的Pareto非支配解。

5 結 論

多目標問題分解得到的子問題往往也是多目標優化問題,本文嘗試求解多目標FJSP的兩階段Pareto優化方法,構建了兩階段混合Pareto蟻群算法,Pareto蟻群系統分別求解多目標作業分派和排序問題。評估操作快速對分派解進行評估,并保留具有較好評估全局解的分派方案作為分派問題的精英檔案,將精英檔案輸入給排序蟻群系統以獲取非支配調度解,最終獲取問題全局非支配前沿。子問題算法混合了與各目標相關的鄰域搜索策略,以提高問題解的質量。通過求解多個基準算例,算法可以獲取現有文獻各算例給出的非支配解,從而驗證了該求解方法的有效性。本文為多目標優化問題的分層Pareto優化方法提供了一種途徑,未來將繼續改進算法,并嘗試應用該算法求解實際調度問題。

表1 工件交付期

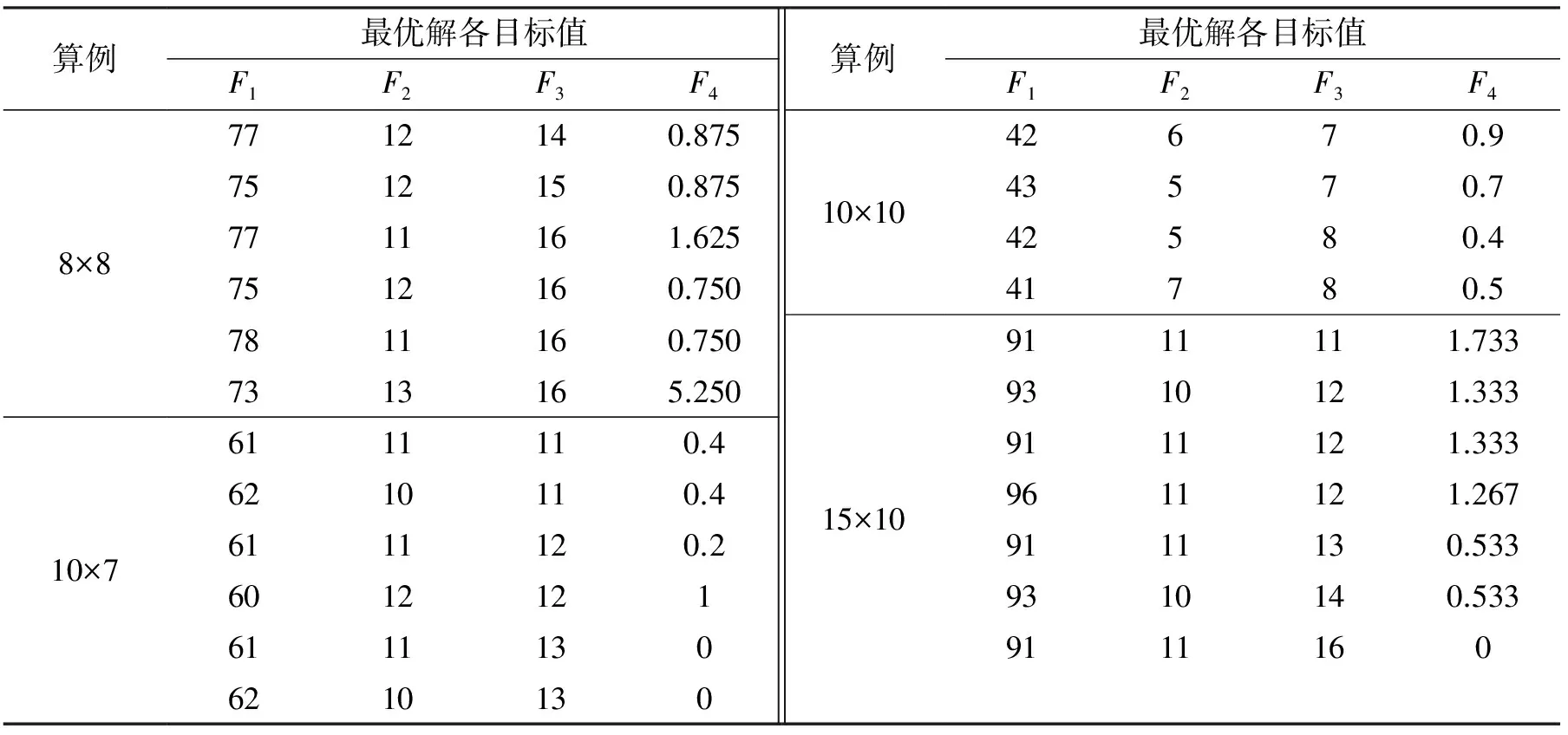
表2 附加平均工件加權延遲時間的部分Pareto最優解

[1] 莫建麟, 吳喆. 基于混合遺傳禁忌的多目標柔性作業車間調度 [J]. 重慶師范大學學報(自然科學版), 2013, 30(2): 87-91. MO Jianlin, WU Zhe. Multi-objective flexible job shop scheduling based on hybrid genetic & tabu algorithm [J]. Journal of Chongqing Normal University (Natural Science), 2013, 30(2): 87-91.

[2] 張超勇, 董星, 王曉娟, 等. 基于改進非支配排序遺傳算法的多目標柔性作業車間調度 [J]. 機械工程學報, 2010, 46(11): 156-164. ZHANG Chaoyong, DONG Xing, WANG Xiaojuan, et al. Improved NSGA-II for the multi-objective flexible job-shop scheduling problem [J]. Journal of Mechanical Engineering, 2010, 46(11): 156-164.

[3] MOSLEHI G, MAHNAM M. A Pareto approach to multi-objective flexible job-shop scheduling problem using particle swarm optimization and local search [J]. International Journal of Production Economics, 2011, 129(1): 14-22.

[4] GAO K Z, SUGANTHAN P N, PAN Q K. Pareto-based grouping discrete harmony search algorithm for multi-objective flexible job shop scheduling [J]. Information Sciences, 2014, 289(1): 76-79.

[5] 張潔, 張朋, 劉國寶. 基于兩階段蟻群算法的帶非等效并行機的作業車間調度 [J]. 機械工程學報, 2013, 49(6): 136-144. ZHANG Jie, ZHANG Peng, LIU Guobao. Two-stage ant colony algorithm based job shop scheduling with unrelated parallel machines [J]. Journal of Mechanical Engineering, 2013, 49(6): 136-144.

[6] XING Lining, CHEN Yingwu. An efficient search method for multi-objective flexible job shop scheduling problems [J]. Journal of Intelligent Manufacturing, 2009, 20(3): 283-293.

[7] XING Lining, CHEN Yingwu. Multi-objective flexible job shop schedule: design and evaluation by simulation modeling [J]. Applied Soft Computing, 2009, 9(1): 362-376.

[8] XIA Weijun, WU Zhiming. An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems [J]. Computers & Industrial Engineering, 2005, 48(2): 409-425.

[9] LI Junqing, PAN Q, LIANG Y C. An effective hybrid tabu search algorithm for multi-objective flexible job-shop scheduling problems [J]. Computers & Industrial Engineering, 2010, 59(4): 647-662.

[10]CHIANG T C, LIN H J. A simple and effective evolutionary algorithm for multi-objective flexible job shop scheduling [J]. International Journal of Production Economics, 2013, 141(1): 87-98.

[11]GARCIA-MARTINEZ C, CORDON O, HERRERA F. A taxonomy and an empirical analysis of multiple objective ant colony optimization algorithms for the bi-criteria TSP [J]. European Journal of Operational Research, 2007, 180(1): 116-148.

[12]DOERNER K, GUTJAHR W J. Pareto ant colony optimization: a meta-heuristic approach to multi-objective portfolio selection [J]. Annals of Operations Research, 2004, 131(1): 79-99.

[本刊相關文獻鏈接]

劉岳鐳,馮祖仁,任曉棟.具有惡化效應的雙代理單機最優調度算法.2016,50(6):9-14.[doi:10.7652/xjtuxb201606002]

陳鵬飛,李昕怡,齊勇,等.單步啟發式策略的備份虛擬機復用策略.2016,50(1):100-107.[doi:10.7652/xjtuxb201601 016]

楊鵬飛,王泉.片上網絡異構多核系統任務調度與映射.2015,49(6):72-76.[doi:10.7652/xjtuxb201506012]

王麗霞,曲樺,趙季紅,等.軟件定義網絡中應用二值粒子群優化的控制器部署策略.2015,49(6):67-71.[doi:10.7652/xjtuxb201506011]

周光輝,苗發祥,李彥廣.數控加工中心任務與刀具集成調度模型及改進自適應遺傳算法.2014,48(12):1-7.[doi:10.7652/xjtuxb201412001]

邵成成,王錫凡,王秀麗,等.主動配電系統與主網的有功協調.2014,48(11):58-63.[doi:10.7652/xjtuxb201411010]

李彬,宋立明,李軍,等.長葉片透平級多學科多目標優化設計.2014,48(1):1-6.[doi:10.7652/xjtuxb201401001]

(編輯 趙煒 杜秀杰)

Two-Stage Hybrid Pareto Ant Colony Algorithm for Multi-Objective Flexible Job Shop Scheduling

ZHAO Boxuan,GAO Jianmin,CHEN Kun

(School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Multi-objective flexible job shop scheduling can be divided into two sub-problems, namely job assignment and sorting, which are often multi-objective optimization problems. Aiming at this situation, this paper presents a layered Pareto optimization frame for multi-objective flexible job shop problem and proposes a two-stage hybrid Pareto ant colony algorithm for multi-objective operation assignment (OA) and operation sequencing (OS) sub-problems. Embedding multiple scheduling rules in GT algorithm is used to evaluate and filter the assignment solutions. The global optimal non-dominated front of the original problem is obtained by scheduling optimization as the elite archive of assignments. Each Pareto ant colony algorithm is combined with the neighborhood search strategies related to different objectives. The co-evolutionary can obtain high-quality solutions to multi-objective FJSP. Finally, by solving four benchmark instances considering minimizing the mean weighted tardiness time, the effectiveness of the method is testified. The simulation results show that the layered Pareto optimization frame helps to reduce complexity of the problem, and compared with other literatures, the proposed algorithm can obtain the Pareto non-dominant solutions of each instance, providing a new way for solving complex multi-objective scheduling problems.

multi-objective flexible job shop scheduling; layered Pareto optimization; two-stage Pareto ant colony algorithm; neighborhood search

2015-11-23。 作者簡介:趙博選(1986—),男,博士生;高建民(通信作者),男,教授,博士生導師。 基金項目:國家科技重大專項資助項目(2012ZX04010-071)。

時間:2016-05-24

10.7652/xjtuxb201607022

F406.2

A

0253-987X(2016)07-0145-07

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160524.1204.002.html