一種基于神經網絡的中制導改進算法

魏倩,蔡遠利

(西安交通大學電子與信息工程學院,710049,西安)

?

一種基于神經網絡的中制導改進算法

魏倩,蔡遠利

(西安交通大學電子與信息工程學院,710049,西安)

針對地球扁率影響下的大氣層外導彈中段制導問題,提出了基于BP神經網絡的模型預測改進算法,并且創新使用軌道偏差解析解來構造訓練樣本集。首先,利用極點變換方法把彈體受到的J2項攝動引力優化分解為與運動軌跡相關的擾動函數;然后,采用偏差狀態空間的轉移矩陣,建立起導彈在J2項攝動作用下的軌道偏差公式;最后,利用偏差公式構造取值廣泛的訓練樣本集并訓練BP神經網絡,從而建立起關于虛擬目標信息的預測模型,計算出中段制導控制所需的增益速度矢量。該模型的優點是利用極點變換和狀態轉移矩陣直接求解J2項攝動偏差,避免了進行大規模的數值積分運算;神經網絡擁有強大的學習能力,保證了預測模型的全面性及精確性;BP神經網絡可以預先離線訓練、學習,大大縮短了計算時間。與傳統Lambert迭代補償修正方法相比,改進型BP神經網絡補償算法可以同時滿足實時計算速度及計算精度的雙重要求,具有較強的實際工程意義。

極點變換;攝動偏差;J2項攝動;BP神經網絡

在大氣層外的遠距離導彈攻防作戰中,彈體的飛行過程分為主動助推段、中段制導段和末制導段。中段制導段是指飛行器在主動段到達關機點后,末段制導開始之前,飛行器進行較長時間的無控滑行過程。在整個中段制導段,飛行器僅采用脈沖推力等方式進行少數幾次飛行狀態修正。因此,整個中段制導階段可以抽象為固定時間的Lambert制導問題,經典方法求解法有傳統高斯解法、普適變量法、Battin-Vaughan算法等[1-5],若考慮地球扁率所產生的J2項引力攝動(引力場函數僅包含2階帶諧項),這些方法會產生較大的軌道偏差。

現階段對于J2攝動下的Lambert制導問題的研究,主要為引力差修正法和補償Lambert制導法[6-11]。引力差修正法是在中段制導過程中,分階段對于引力差所產生的軌道偏差進行彈道修正,其優點是制導精度對于飛行狀態參數的魯棒性較好,缺點是引力差的計算進行了大量的近似處理,且修正過程持續整個中制導階段。補償Lambert制導法是在經典Lambert制導基礎上,補償修正J2引力攝動對飛行彈道的影響,是一種簡單、實用的制導方法。但是,現有的補償制導法在計算精度和運行時間兩方面難以取得平衡,限制了上述方法在實際工程中的應用。

本文提出了基于BP神經網絡的模型預測制導算法,并使用偏差解析解來構造取值廣泛的訓練樣本集,這可大大縮短計算時間,滿足實時在線計算的要求。

1 改進Lambert制導問題描述

在研究Lambert制導時,通常假設飛行器可以瞬間獲得轉移軌道所需要的速度增益矢量,不涉及脈沖推力控制問題。

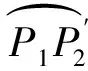
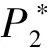
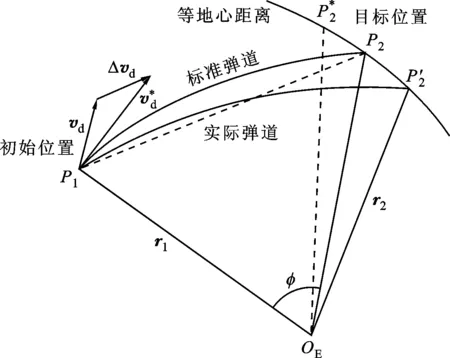
圖1 經典Lambert制導下目標點P2與虛擬目標點

2 軌道偏差解析解

2.1 J2項引力攝動的分解

彈體受到的J2項引力函數可表示為[1]

(1)

式中:r為地心距;φ為地心緯度;ae=6 378 137;J=1.082 6×10-3。

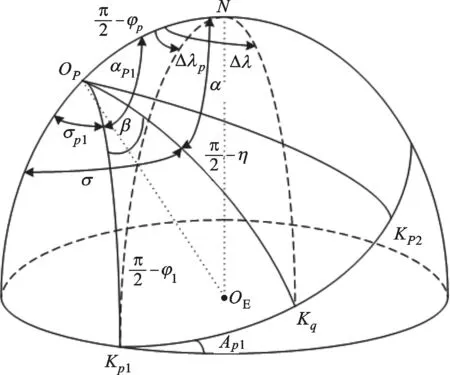
圖2 極點變換的幾何關系

關于極點Op(λp,φp)可由初始點P1位置信息得到,即

(2)

因此,標準橢圓軌道上任意點Q(λ,φ),變換出的新坐標(η,σ)關系式為

(3)

J2項引力攝動的加速度,關于導彈軌跡運動的分量表示為

(4)

其中

(5)

2.2 軌道偏差解析解

為避免直接求解微分方程帶來的困難,本文采用偏差狀態的轉移矩陣直接解算出軌道偏差的解析解。

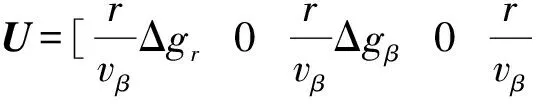
(6)

當考慮到實際軌道與標準橢圓軌道同為地心距r時,軌道狀體參數的偏差稱為等地心距偏差。設等地心距偏差構成的狀態向量為

(7)

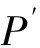
(8)

其中

(9)

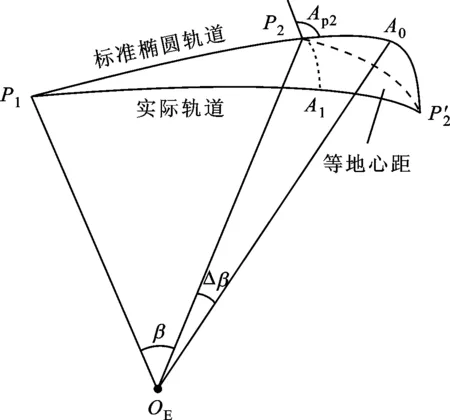
圖3 等地心距偏差與等地心角偏差的關系

因此,Yr的攝動偏差方程表示為

(10)

由于J2項引力擾動,導彈的軌道偏差可分解為東向和北向兩個方向

(11)

式中:Ap2為目標點P2的方位角。

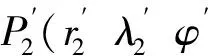
(12)

3 改進型Lambert制導算法

3.1 虛擬目標點預測模型

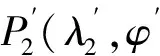
考慮到Lambert制導問題對于預測精度的要求,引入多隱含層來提高網絡預測精度。通過對比分析,采用網絡結構為3-9-9-3的4層BP神經網絡滿足模型的預測精度。

使用BP神經網絡建模時,訓練樣本的選取十分重要。訓練樣本滿足2個條件:①樣本數量要足夠多,能夠反映出關系的復雜程度;②樣本需要具有代表性,盡可能包含各種特征模式。

在大氣層外導彈的取值范圍內以任務目標點P2為中心選取采樣數據,構成采樣矩陣Ti,j,k(λTi,φTj,tTk),滿足條件

(13)

式中:Δλ、Δφ、Δt為小量的采樣間隔;i=0,±1,±2,…,±nλ,j=0,±1,±2,…,±nφ,k=0,±1,±2,…,±nt,nλ、nφ和nt分別決定在λ、φ和tF上采樣規模的大小。

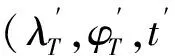
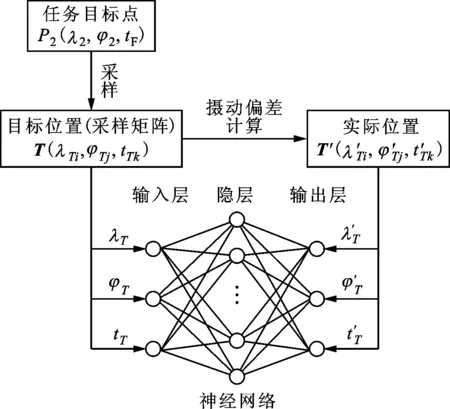
圖4 神經網絡訓練原理圖

因為Δλ、Δφ取值較小,采樣樣本集中分布在目標點周圍一定的范圍內,此樣本集減小了J2項引力攝動對位置、飛行時間等的復雜影響,使得樣本的輸出信息也在小范圍內變化,小范圍變化的各種因素使得映射關系接近于線性關系。同時,此采樣集兼顧考慮了時間、空間等因素不同數量級變化對于飛行軌道偏差的實際影響。

3.2 制導方法流程

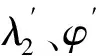
4 算法驗證與分析

假設遠距離飛行的導彈只受到J2項引力攝動作用的影響,且不進行導彈末段制導修正,通過仿真實驗對以上改進型Lambert制導算法的正確性、可靠性和精度進行驗證。

4.1 仿真算例分析

取導彈關機點P1在地心東經緯度為0°、北緯經度為10°、高度為1 200 km處,用2個具體算例來對比分析。在算例1中,假設導彈的任務目標信息為(46.2°,7°,1 150 s)。在考慮到J2項引力攝動下,導彈的無修正落點為(46.260 4°,7.006 5°,1 148 s),落點誤差6 754 m。通過BP神經網絡預測出虛擬目標點(46.139 7°,6.993 6°,1 151.6 s),BP改進算法的修正效果良好,修正落點誤差僅為7.6 m。在算例2中,假設導彈的任務目標為(35°,17°,800 s)。在考慮到J2項引力攝動下,導彈的無修正落點為(34.959°,16.985°,796.6 s),落點誤差為4 844 m。通過BP神經網絡預測出虛擬目標點(35.040 8°,17.015 3°,803.3 s),修正落點誤差僅為2.972 m。

通過對2個算例數據對比可看出:在J2項引力攝動的影響下,導彈的位置偏差為104m,并且偏差隨著飛行時間的延長、飛行距離的增長而不斷變大;改進型算法利用BP神經網絡預測出虛擬目標點,可很好修正J2項引力攝動引起的軌道位置偏差。

根據BP神經網絡訓練樣本的選取規則,算例1中,將任務目標點的信息(46.2°,7°,1 150 s)作為BP神經網絡的訓練樣本的采樣中心點,nλ=10、nφ=10、nt=5、Δλ=0.57°、Δφ=0.57°、Δt=20 s,采樣樣本個數為4 851,隨機抽取4 751個樣本作為訓練樣本,剩余的100個樣本作為測試數據。

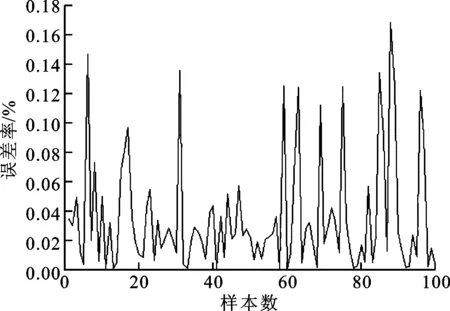
圖5 算例1的測試誤差率

利用算例1中的訓練數據對預先訓練完成的BP神經網絡(BPnet)進行第2次更新訓練,迭代次數為100,均方誤差為10-6。由于BPnet網絡經過預先訓練過程,二次訓練的迭代次數為3,訓練誤差為9.37×10-7,運行時間為1.3 s,測試樣本數據的誤差為9.6×10-6,測試誤差率如圖5所示。對于算例2進行相同的神經網絡訓練,得到二次訓練的迭代次數為1,訓練誤差為8.6×10-7,運行時間為1.64s,測試樣本誤差為8.5×10-6,測試數據的測試誤差率如圖6所示。對于BPnet網絡的二次更新訓練,使得靜態BP神經網絡能夠滿足不同任務目標點的相關要求,并且在同一任務目標點周圍一定區域中,BP神經網絡具有較好的預測能力。

通過2個算例的仿真計算可看出,本文討論的基于BP神經網絡的改進型Lambert制導算法,可很好修正J2項攝動產生的軌道偏差,實現精確的飛行制導。

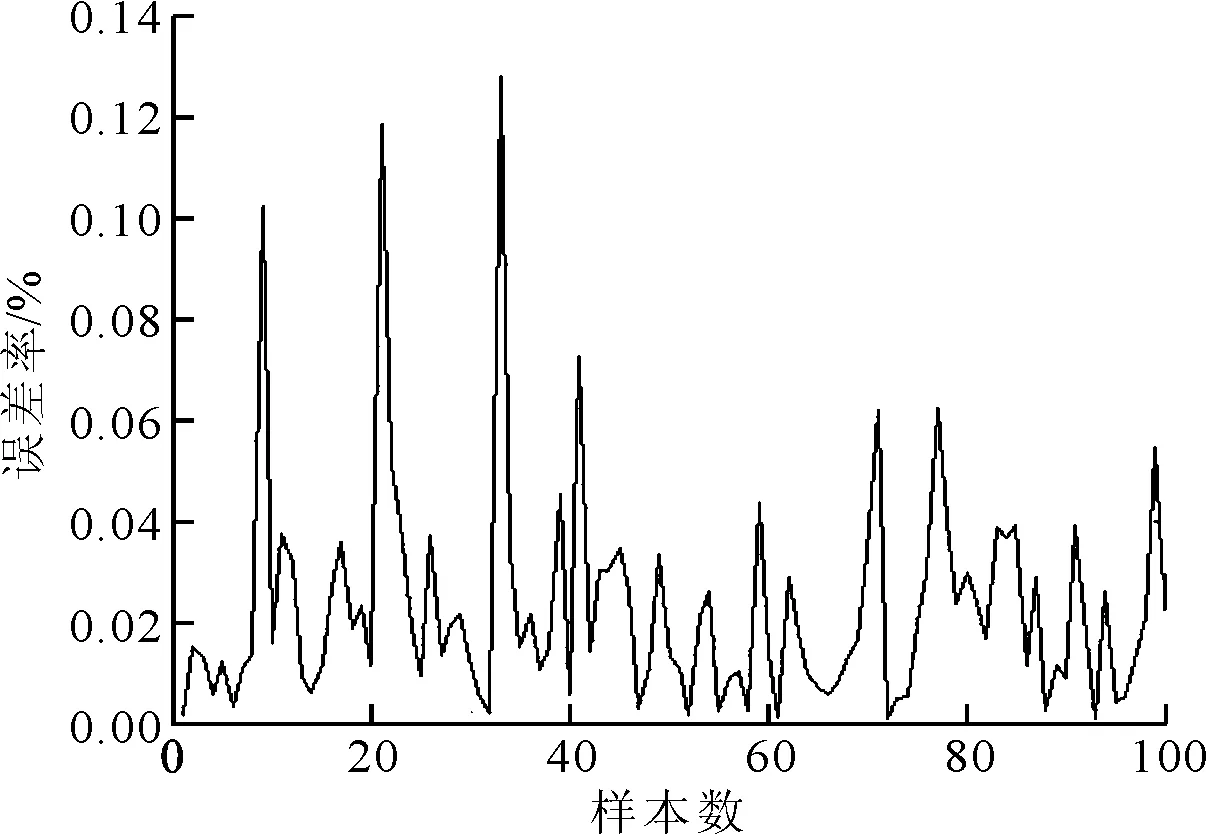
圖6 算例2的測試誤差率

4.2 算法對比與分析

忽略關機點測量誤差,且不進行末制導修正,在相同的運算環境下分別用BP神經網絡改進法及經典虛擬目標補償修正法進行對比仿真分析。不同算法的仿真精度、計算結果以及所耗費的運行時間如表1所示。

表1 不同算法的仿真效果對比

經典的虛擬目標點補償法[1]采用數值積分,整個飛行仿真周期為50 s,計算出位置偏差并進行迭代修正,次數一般不小于3,數值積分所耗費的時間相當可觀,并且軌道積分的路徑差別也影響計算精度。改進型算法使用BP神經網絡建立目標點與實際位置之間的映射關系,從而可精準預測出虛擬目標點信息。

仿真對比實驗結果表明,BP神經網絡改進型Lambert制導策略在計算精度相當的情況下,具有運算量小、方法簡便、易于工程實現等優點。

5 結 論

考慮J2項攝動影響的Lambert問題是一個典型的多變量非線性問題,常規方法不能滿足計算時間和運算精度的雙重要求。本文利用偏差解析解構造出基于BP神經網絡的預測模型,并計算得到補償制導的控制參數,其最主要的優點是:利用狀態轉移矩陣直接求解J2項攝動引起的軌道偏差,避免了進行大規模的數值積分運算;神經網絡的強大學習能力,保證了預測模型的全面性以及精確性;BP神經網絡的離線訓練、學習,大大縮短了計算時間。此改進型制導算法可同時滿足實時計算效率及計算精度的雙重要求,具有較大的實際工程意義。

[1] BATTIN R H. Introduction to the mathematics and methods of astrodynamics [M]. Reston, VA, USA: AIAA, 1999: 325-417.

[2] AHN J, lEE S. Lambert algorithm using analytic gradients [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(6): 1751-1761.

[3] AHN J, BANG J, LEE S. Acceleration of zero-revolution Lambert’s algorithms using table-based initialization [J]. Journal of Guidance, Control, and Dynamics, 2015, 38(2): 335-342.

[4] ZHANG Gang, CAO Xibin, ZHOU Di. Two-impulse cotangent rendezvous between coplanar elliptic and hyperbolic orbits [J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 965-969.

[5] WAILLIEZ S E. On Lambert’s problem and the elliptic time of flight equation: a simple semi-analytical inversion method [J]. Advances in Space Research, 2014, 53(5): 890-898.

[6] 高海燕, 蔡遠利. 高超聲速飛行器的滑模預測控制方法 [J]. 西安交通大學學報, 2014, 48(1): 67-72. GAO Haiyan, CAI Yuanli. Sliding mode predictive control for hypersonic vehicle [J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 67-72.

[7] 徐明, 譚田, 李志武, 等. Lambert轉移中途修正的全局概率最優策略 [J]. 北京航空航天大學學報, 2012, 38(5): 574-578. XU Ming, TAN Tian, LI Zhiwu, et al. Optimal correction strategy during Lambert transfer from view of probability [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5): 574-578.

[8] 胡正東, 郭才發, 曹淵, 等. 軌道轟炸飛行器過渡段軌道設計與制導 [J]. 固體火箭技術, 2009, 32(5): 473-479. HU Zhengdong, GUO Caifa, CAO Yuan, et al. Transition trajectory planning and guidance for orbital bombing vehicle [J]. Journal of Solid Rocket Technology, 2009, 32(5): 473-479.

[9] 柴華, 仲明, 梁彥剛. 采用狀態轉移矩陣的攔截中段制導方法 [J]. 國防科技大學學報, 2015, 37(4): 137-142. CHAI Hua, ZHONG Ming, LIANG Yangang. Midcourse guidance of interception using state transition matrix [J]. Journal of National University of Defense Technology, 2015, 37(4): 137-142.

[10]鄭偉, 湯國建. 擾動引力場中彈道導彈飛行力學 [M]. 北京: 國防工業出版社, 2009: 32-45.

[11]YAMADA K, KIMURA M. New state transition matrix for formation flying inJ2-perturbed elliptic orbits [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 536-547.

[12]鄧一兵, 胡偉, 高峰, 等. 遺傳神經網絡在載人飛船環控決策系統中的應用研究 [J]. 西安交通大學學報, 2010, 44(7): 64-69. DENG Yibing, HU Wei, GAO Feng, et al. Application of genetic neural network to decision support system for environmental control and life support system [J]. Journal of Xi’an Jiaotong University, 2010, 44(7): 64-69.

[本刊相關文獻鏈接]

張小棟,郭晉,李睿,等.表情驅動下腦電信號的建模仿真及分類識別.2016,50(6):1-8.[doi:10.7652/xjtuxb201606001]

姜濤,黃偉,王安麟.多路閥閥芯節流槽拓撲結構組合的神經網絡模型.2016,50(6):36-41.[doi:10.7652/xjtuxb201606 006]

宋青松,田正鑫,孫文磊,等.用于孤立數字語音識別的一種組合降維方法.2016,50(6):42-46.[doi:10.7652/xjtuxb2016 06007]

陳江城,張小棟.人體下肢行走關節連續運動表面肌電解碼方法.2016,50(6):61-67.[doi:10.7652/xjtuxb201606010]

陳斌,胡平舸,屈丹.子空間域相關特征變換與融合的語音識別方法.2016,50(4):60-67.[doi:10.7652/xjtuxb201604010]

王安麟,孟慶華,曹巖,等.液力變矩器的葉片數神經網絡模型.2015,49(7):11-16.[doi:10.7652/xjtuxb201507003]

馬忠麗,文杰,梁秀梅,等.無人艇視覺系統多類水面目標特征提取與識別.2014,48(8):60-66.[doi:10.7652/xjtuxb2014 08011]

侯雨伸,王秀麗.氣象過程信息挖掘與輸電線路覆冰預測.2014,48(6):43-49.[doi:10.7652/xjtuxb201406008]

王萬召,王杰.采用限定記憶極限學習機的過熱汽溫逆建模研究.2014,48(2):32-37.[doi:10.7652/xjtuxb201402006]

馮斌,梅雪松,楊軍,等.數控機床摩擦誤差自適應補償方法研究.2013,47(11):65-69.[doi:10.7652/xjtuxb201311012]

(編輯 趙煒)

A Modified Algorithm on the Midcourse Guidance Based on BP Neural Network

WEI Qian,CAI Yuanli

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Aiming at solving the midcourse guidance problem of exo-atmosphere missile under the influence of earth’s oblateness perturbation, a prediction model for missile guidance was proposed based on BP neural network. This method provides a new training sample set constructed by the analytical formula of trajectory deviation. First, by using the pole transform method, the missile’sJ2perturbed gravity is decomposed into the disturbing function related to its flight trajectory. Then, with the state space matrix method, the analytic solution of trajectory deviation with theJ2perturbation is calculated. Finally, using trajectory deviation function to construct a wide range of training sample set, the BP neural network of prediction model is established. The neural network can forecast the virtual target point information, so as to calculate the vector of gained velocity for midcourse guidance control. Using the modified algorithm, the trajectory deviation ofJ2perturbation can be directly solved by pole transform and state transition matrix, avoiding large-scale numerical calculation. The BP neural network has powerful learning and training ability, ensuring the comprehensiveness and accuracy of the prediction model and saving calculation time by the off-line training and learning before the simulation tests. In comparison with traditional correction method of Lambert guidance, this modified algorithm can satisfy the requirements on both efficiency and accuracy of real-time computation, being of practical engineering significance.

pole transform; perturbation deviation;J2perturbations; BP neural network

2015-12-04。 作者簡介:魏倩(1984—),女,博士生;蔡遠利(通信作者),男,教授,博士生導師。 基金項目:國家自然科學基金資助項目(61308120,61463029)。

10.7652/xjtuxb201607019

V448.2

A

0253-987X(2016)07-0125-06