機場應急投送能力評估模型的構建

夏軍劍，夏愛生，劉俊峰，張新巍

(軍事交通學院 基礎部，天津 300161)

?

● 基礎科學與技術 Basic Science & Technology

機場應急投送能力評估模型的構建

夏軍劍，夏愛生，劉俊峰，張新巍

(軍事交通學院 基礎部，天津 300161)

針對機場應急投送能力評估問題，采用多類顧客閉合排隊網絡建立性能評價模型，對平均值分析算法提出具體處理方法，使之適應多類飛機型號、多種運輸任務的需求，并運用模型進行了理論計算。通過將計算結果與蒙特卡洛仿真結果對比分析表明，建立的模型反映了真實系統的性能變化趨勢；通過模型分析，可以發現系統的瓶頸資源，預測系統某個服務中心服務臺數量的變化對整個系統的影響程度。

投送能力評估；MVA算法；閉排隊網絡；蒙特卡洛仿真；出動架次率

航空運輸是戰略投送的主要手段，加強航空運輸能力是戰略投送能力建設的重要部分。機場是航空運輸系統中的重要基礎設施，是連接航空運輸和其他運輸方式的橋梁和紐帶，是運輸網絡的重要節點。隨著航空運量的快速增長，對機場的運輸能力也提出了更高的要求。機場設施建設需要占用大量資金，因而對整個空運系統進行分析和優化，有助于機場進行科學管理，優化設施配置，降低建設成本，改善運輸質量，提高運輸效率，避免資源浪費。

對于航空運輸能力，架次率是衡量其能力的一個重要指標[1]。常用的出動架次率的計算方法有類比法、解析法和仿真法。仿真法能精確分析，國內外研究成果比較多[2-4]，但仿真模型適應性差，建模復雜，計算耗時。孫蛟等[5]提出了基于時間分割思想的工程計算方法，建立了出動架次率計算模型，但只計算了單架飛機的時間指標。飛機從機場起飛至回到機場，可以認為是一個封閉的系統，出動回收的流程中任一環節都可看成顧客到達服務然后離開的過程，可以運用閉排隊網絡的成熟理論進行建模與分析。通常利用均值(如平均服務時間、平均到達速率)來參數化排隊模型，利用均值分析法(mean value analysis，MVA)求解[6]。Dietz等[7]提出將Fork-Join閉排隊網絡的MVA法應用于飛機架次率的建模分析上，獲得了飛機出動架次率的解析結果。夏國清等[8]提出一種共享服務器的MVA法，并用于飛機出動能力的研究中。本文提出將多種顧客源的時間參數均值化的方法，結合閉排隊網絡模型，得到整個系統的性能參數，用于分析機場的應急投送能力，最后通過仿真模型進行對比和驗證。

1 機場應急空中輸送系統分析

機場應急投送系統是戰略投送系統重要的子系統，其作業流程可分為5部分：飛行前準備、飛行與飛行后檢查、預防性維修、修復性維修、物資裝備裝卸載(人員登離機)和加油。其中，在充分利用飛機的裝載能力的情況下，某型號的飛機裝卸時間和加油時間幾乎是固定的。

整個應急投送系統作業流程如圖1所示。整個過程可以將運輸機看作客戶，各種活動為運輸機接受的服務，基本符合閉排隊網絡的條件，即客戶只在網絡內部轉移，且沒有外部客戶到達，可以建立機場應急投送系統的閉排隊網絡模型。

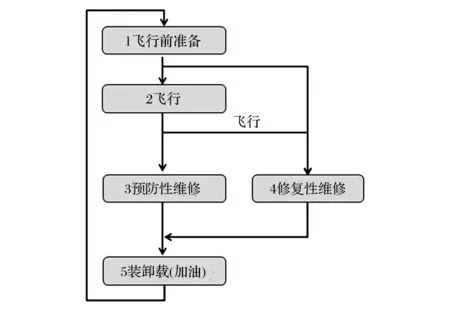
圖1 機場應急投送系統作業流程

為了表達方便，定義飛行前準備、飛行、預防性維修、修復性維修、裝卸載(加油)分別用節點1—5表示。由于運輸機型號不同、服役時間不同、運輸任務不同，因此整個機場應急投送系統可以認為具有K類顧客，每類顧客具有Nk(k= 1,2,…,K)個客戶，有M個服務中心的閉排隊網絡模型。第k(k= 1,2,…,K)類顧客的每架運輸機在第i服務中心完成服務后，以一定概率pkij轉移到服務中心j，可以用矩陣Pk(k= 1,2,…,K)描述。在整個系統中，架次率可用單位內“飛行位”的吞吐量表示。飛機在各服務中心轉移并接受服務，本文假定各服務中心服務時間都服從負指數分布。服務中心服務器的數量為同時接受服務的飛機數量，反映各節點的服務能力。

2 機場應急空中輸送系統保障能力計算方法

對于閉排隊網絡求解的常規方法是平均值分析方法[9]。本文的顧客種類呈現多樣化，因此，服務節點的服務時間不能用同一分布表示。本文提出對服務時間平均值的計算方法進行近似處理而得到近似平均值分析法來求解閉排隊網絡模型。

2.1 狀態轉移矩陣和服務時間平均值計算方法

對任意服務中心i*，第k類顧客平均每到達服務中心i*一次，相應到達服務中心i的次數滿足方程[6]：

(1)

式中：Pk為第k(k= 1,2,…,K)類顧客的狀態轉移矩陣；vk為一向量。

為計算第k類顧客執行一次飛行任務的平均周轉時間，設定i*=2，令vk2=1，則得到飛機在服務中心i的吞吐量與“飛行”狀態吞吐量之比vk=[vk1，vk2,…，vkM]。

于是，第k類顧客執行一次飛行任務平均周轉周期為

(2)

式中tki為第k類顧客在節點i的平均服務時間。

第k類顧客飛行架次率rk為

(3)

第k類顧客在第i個服務中心占有比例ηki為

(4)

第i個服務中心等效平均服務時間ti為

(5)

系統內的顧客數量N為

(6)

k類顧客平均的等效狀態轉移矩陣的項為

(7)

通過以上處理方法，我們最終得到一個有N個顧客、M個服務中心、狀態轉移矩陣為P=[pij]、第i個服務中心服務時間為ti的閉排隊網絡模型。

2.2 MVA算法

到達定理(arrival theorem)是MVA算法的理論基礎。它證明了在一個封閉的網絡中，如果有N個客戶，一個剛到達節點的客戶看到的到達此節點的客戶數量的分布，為該系統中少一個客戶(N-1)時的此節點的客戶數量的分布。由到達定理可得

μi(n)Pi(n|N)=λi(N)Pi(n-1|N-1)

(8)

式中：Pi(n|N)為在網絡中有N個客戶的情況下，第i個服務臺有n個客戶的概率；λi(N)為在網絡中有N個客戶時，客戶到達第i個服務臺的速度(由于穩定狀態下客戶到達的速度等于離去的速度，所以也可以稱λi(N)為吞吐量)；μi(N)為第i個服務臺有n個客戶時的服務速度：

(9)

式中ti為第i個服務中心的服務時間。

客戶在第i個服務中心的停留時間為

(10)

根據式(3)可以得到，客戶在整個網絡中的循環周期是客戶兩次經過同一個服務中心的平均時間。顯然，不同的服務中心對應循環周期是不一定相同的。為便于討論，將循環周期定義為客戶兩次到達服務中心2的平均時間間隔：

(11)

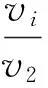
令V=(v1，v2，…,vM)，設v2=1，則V=VP，因為路徑轉移矩陣P是不可約的，所以V有唯一解。

根據客戶在閉排隊網絡的循環周期，可以計算網絡中有N個客戶時各個服務中心吞吐量：

(12)

根據Little定理可得，第i個服務中心總的客戶數量Qi(N)和正在接受服務的客戶數量Qs,i(N)為

Qi(N)=Ri(N)λi(N)

(13)

Qs,i(N)=tiλi(N)

(14)

第i個服務中心的服務器利用率即為正在接受服務的客戶數量與服務器數量比值：

Ui(N)=Qs,i(N)/ri

(15)

對式(8)稍加變動即可得到式(16)，從而可以計算出客戶分布Pi(n|N)：

Pi(n|N)=λi(N)Pi(n-1|N-1)/μi(n)

(16)

(17)

以上方程揭示了排隊網絡中有N個客戶和N-1個客戶時的概率分布關系。若知N-1個客戶時的概率分布，就可以推算出有N個客戶時的概率分布。對于任何排隊網絡都有N=1時，Pi(0|N-1)=1和Qi(N-1)=0，由此經過迭代運算，可求得閉排隊網絡中有任意客戶時的分布。

2.3 多類顧客分布情況和吞吐量計算

由公式(4)、(13)，可以得到第k類顧客在第i個服務中心總客戶數量Qki(N)：

Qki(N)=Qi(N)ηki

(18)

由公式(4)、(12)，可以得到第k類顧客在第i個服務中心總吞吐量λki(N)：

λki(N)=λi(N)ηki

(19)

3 實例分析

以3種類型的飛機執行多種運輸任務為例，劃分顧客種類，給出了各服務中心的平均服務時間、已配置的服務臺數目。假定服務時間都服從負指數分布(見表1)。飛機到達飛行前準備和飛行兩個服務中心不需要等待，能立刻被處理，所以服務器的數目設為無窮。其他服務中心都配備了有限數目的服務器。

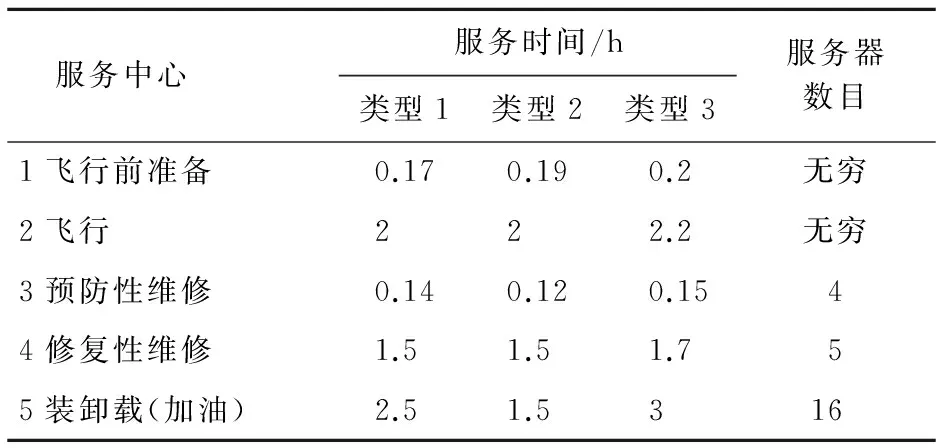
表1 出動回收過程相關參數

3類飛機的狀態轉移概率矩陣為

由公式(1)—(7)計算可得平均周轉時間：T1=5．176 1 h、T2=4．187 9 h、T3=5．973 3 h。

飛機數量N=50，各服務中心平均服務時間和顧客在服務中心占有比率見表2。

由表2可以看出，雖然總的飛機數相同，但不同類型的顧客有不同的周轉時間，所以周轉時間長的實際占有比例要偏小，周轉時間短的實際占有比例偏大。

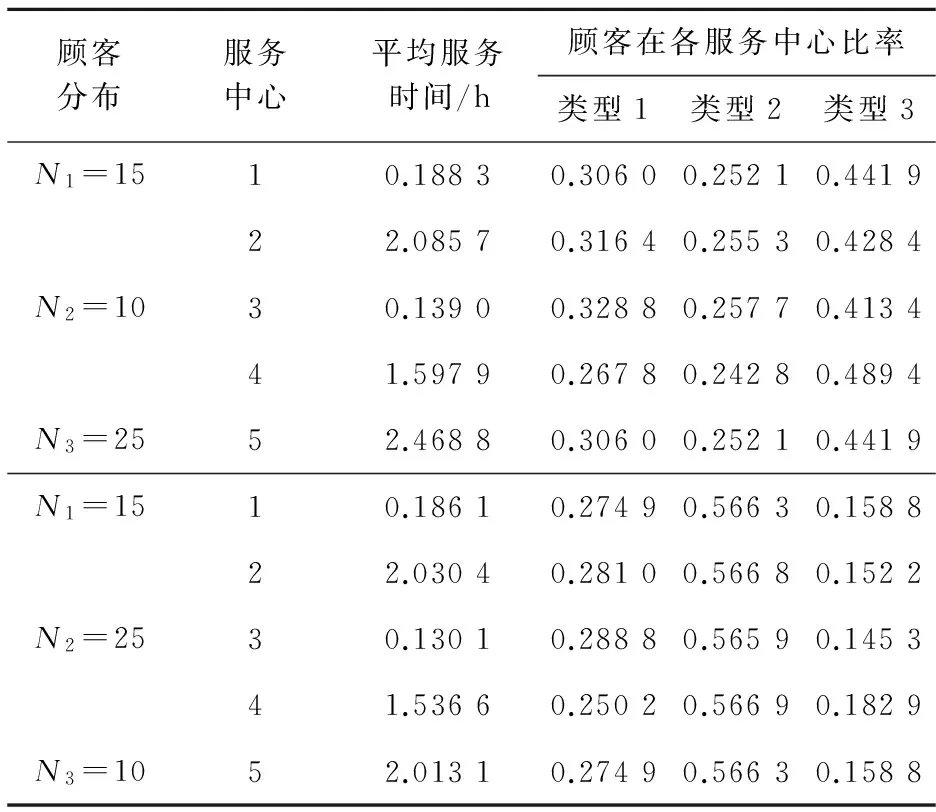
表2 顧客在各服務中心比率計算結果

對于平均狀態轉移概率矩陣，當N1=15、N2=10、N3=25時：

當N1=15、N2=25、N3=10時：

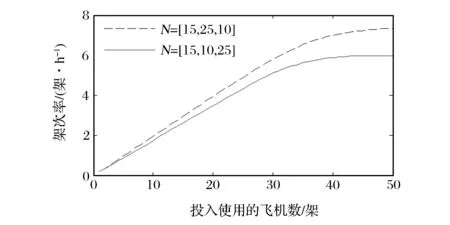
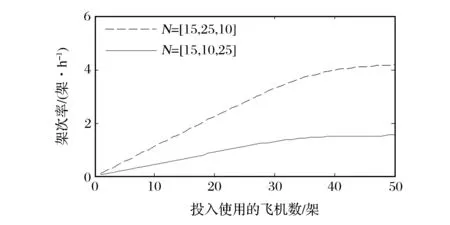
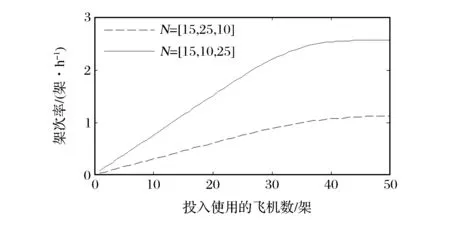
使用MVA算法后得到架次率如圖2所示，雖然飛機總數一致，但由于類型比重不同，所以總體的架次率是不一致的。當三者比重為15∶10∶25時，N<30時呈線性上升趨勢，N>40時，趨勢平緩；當三者比重為15∶25∶10時，N<35時呈線性上升趨勢，N>45時，趨勢平緩。說明不同類型的顧客對資源的需求是不一樣的，周轉時間短的顧客占用資源少，可以得到更多的出動架次率，周轉時間長的顧客占用資源多，出動架次要少。不管是哪一種比率，當架次率增加趨于平緩時，單純增加飛機數量已經不能提高飛機的出動能力。服務中心利用率如圖3所示，可以看出飛機出動的瓶頸在裝卸載(加油)環節，隨著飛機數量的增加，裝卸載(加油)環節首先達到100%，所以制約架次率的關鍵因素是裝卸載(加油)環節。

(a)3種類型飛機

(b)類型1飛機

(c)類型2飛機

(d)類型3飛機

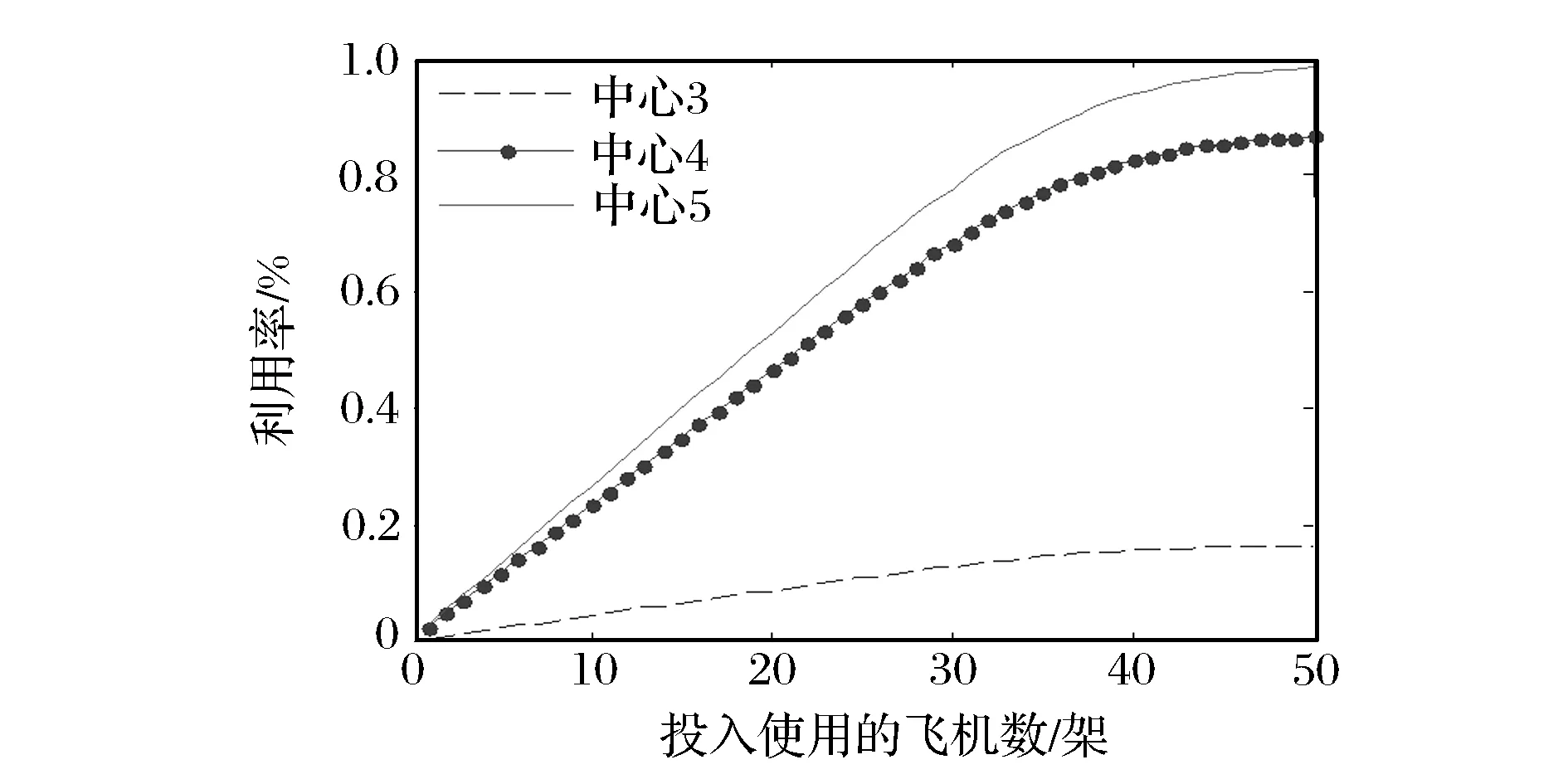
(a)N=[15，25，10]時

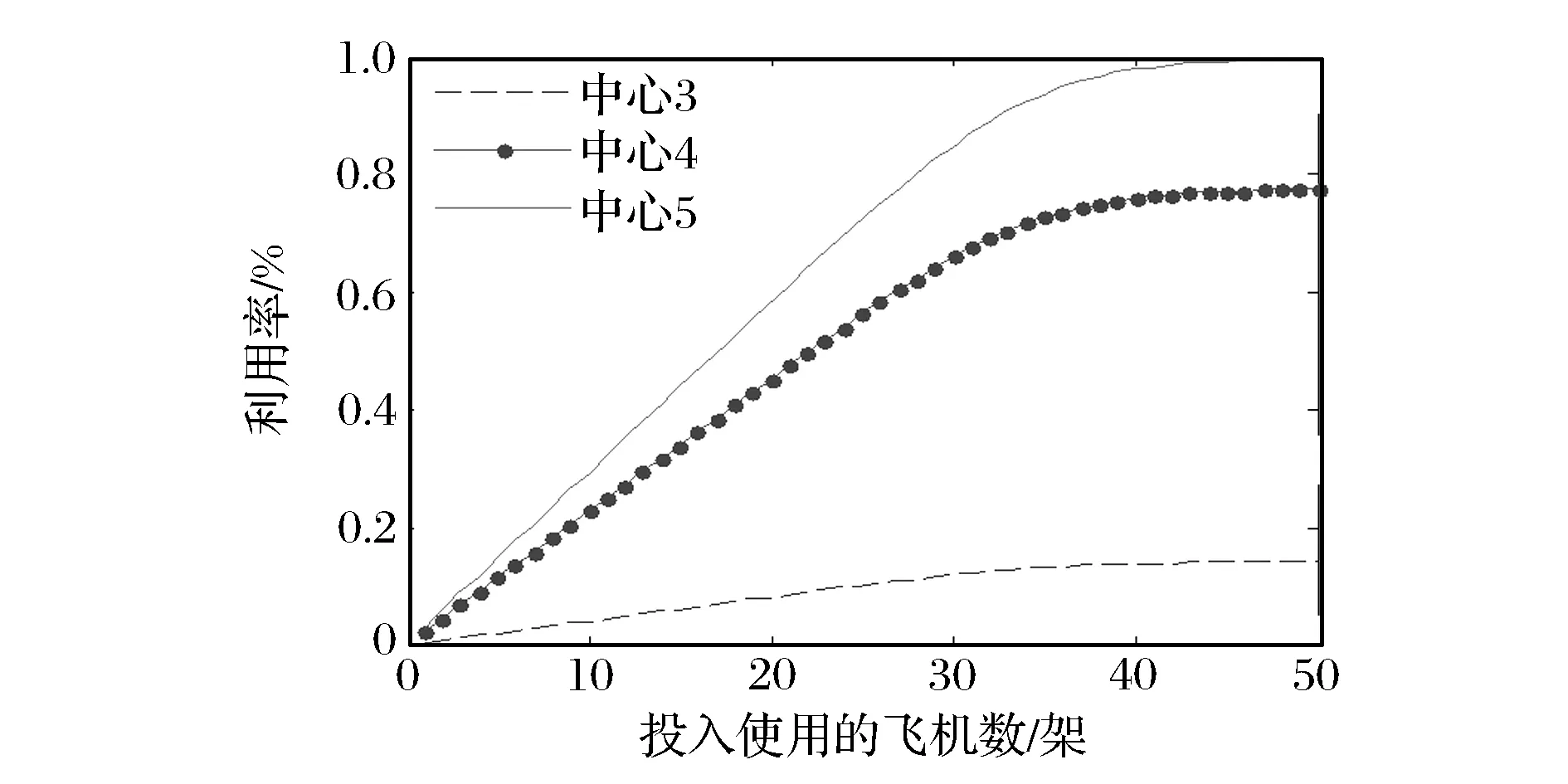
(b)N=[15，10，25]時

由公式(18)、(19)可求出各種類型顧客實際的吞吐量和在各服務中心的顧客數(見表3、4)。

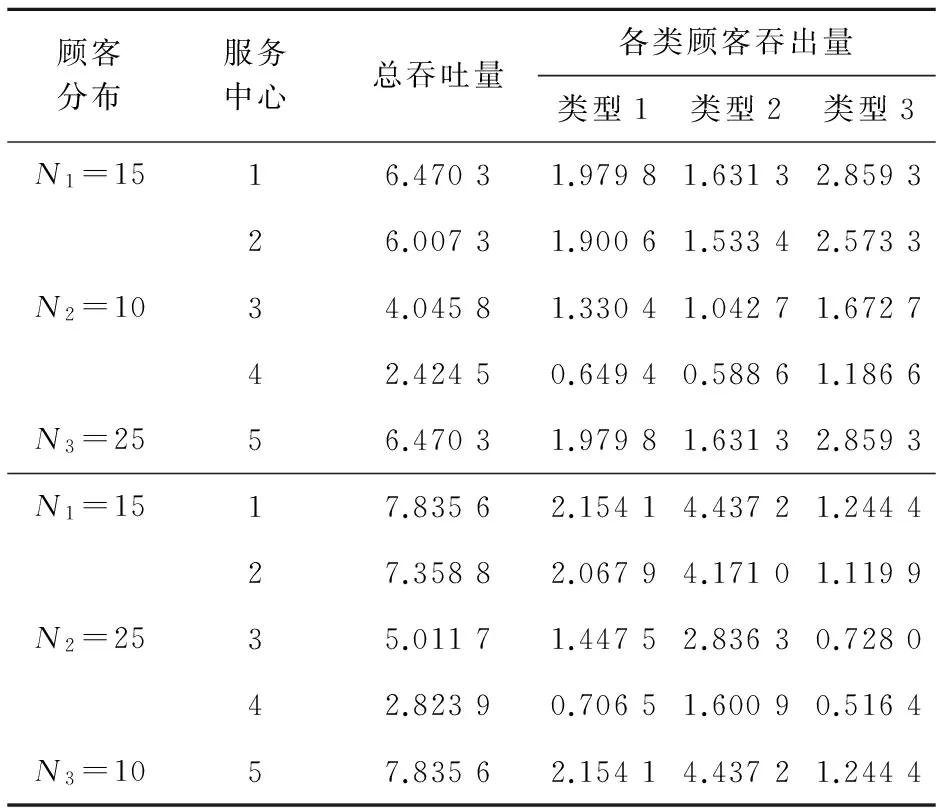
表3 吞吐量數據

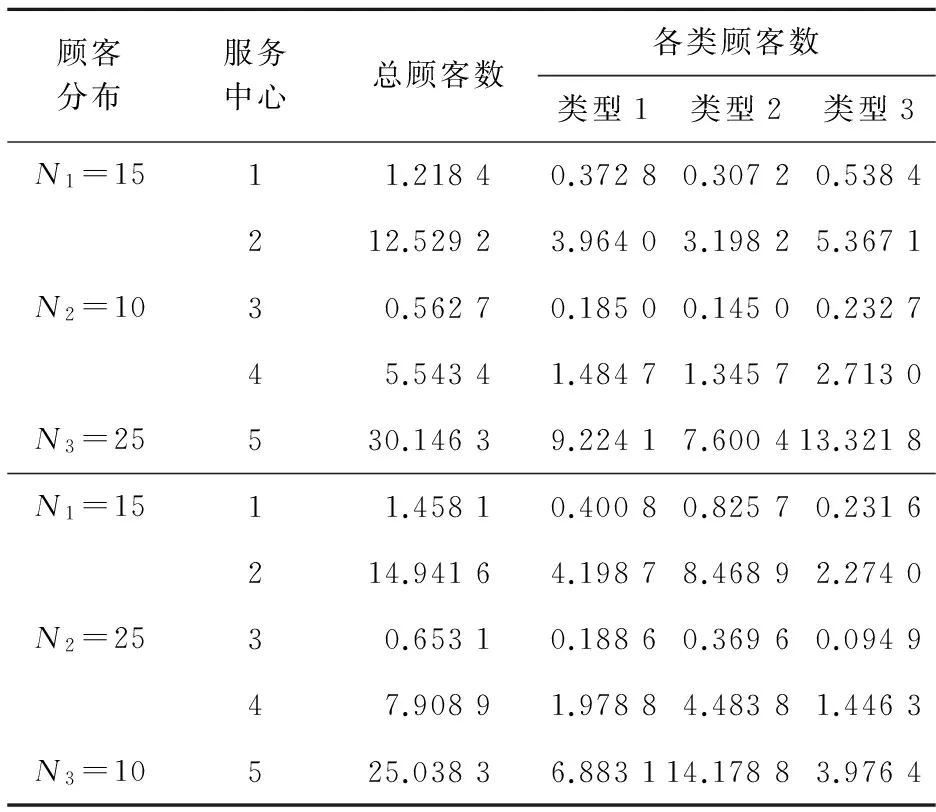
表4 各服務中心顧客數

為了對所建模型的性能指標進行驗證，基于模特卡羅方法建立了多顧客閉排隊網絡系統的仿真模型，仿真時間5×103h，按N= 30、N= 50兩種情況為例進行模擬。表5為本文建立的解析方法和仿真結果的對比數據，從表5各服務中心吞吐量和利用率的數據可以看出本文的解析模型能正確地對機場的性能進行評價。

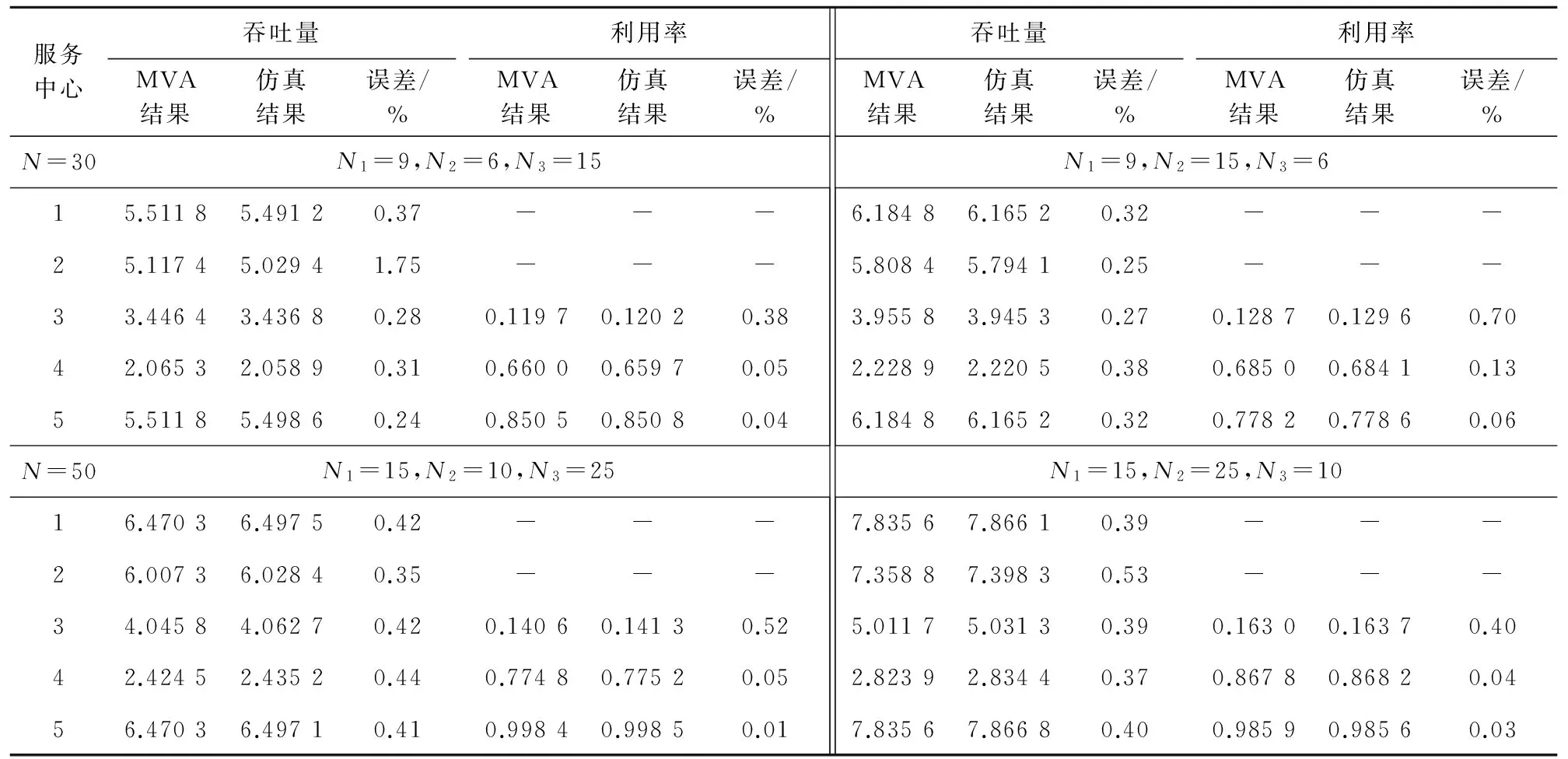
表5 MVA算法和仿真的服務中心吞吐量和利用率對比結果

4 結 語

對于機場應急投送能力問題，基于閉排隊理論建立解析模型。該模型充分考慮了不同類型飛機執行不同運輸任務的情況，對所給參數進行了平均值處理，利用MVA算法求出飛機出動架次率，為應急投送提供參考。通過模型的結果與仿真結果的對比，說明所建解析模型是合理的，可以在投送任務開始前有效地對機場的實際投送能力進行評價，實現對人員、物資、裝備的合理調配，為決策者制訂決策方案提供理論支持。

[1] 國防科工委綜合計劃部．裝備綜合保障通用要求:GJB 1999—3872[S].北京:國防科工委軍用標準化中心,1999:15.

[2] HARRIS J W. The Sortie Generation Rate Model[C]//Proceedings of the 2002 Winter Simulation Conference, 2002:864-868.

[3] PATTINGGILL K B.An analysis of the efficacy of the logistics composite model in estimating maintenance manpower productive capacity[D].Dayton: American Air Force Institute of Technology,2003:13-45.

[4] 方紹強,衛克,陳偉鵬.基于ARENA的戰場飛行保障過程建模與仿真[J].系統仿真學報,2008, 20(3):746-750.

[5] 孫蛟,趙彬,辛文逵.軍用飛機出動架次率工程計算方法[J].空軍裝備研究,2009,3(6):30-33.

[6] REISER M,LAVENBERG S S.Mean-value analysis of closed Multichain queueing networks[J].Journal of the ACM,1980,27(2):313-322.

[7] DIETZ D C,JERKINS R C.Analysis of aircraft sortie with the use of a fork-join queueing network mode[J].Naval Logistics Research,1997,2(44):153-164.

[8] 夏國清,陳紅召,王元慧.基于閉排隊網絡的飛機出動架次率分析[J].系統工程學報,2011,26(5): 686-693.

[9] GUO L W, AU O C, MA M Y, et al. A novel analytic quantization-distortion model for hybrid video coding [J].IEEE Transcations on Circuits and Systems for Video Technology,2009,19(5):627-641.

(編輯：張峰)

Construction of Airport Emergency Projection Ability Evaluation Model

XIA Junjian, XIA Aisheng, LIU Junfeng, ZHANG Xinwei

(General Courses Department, Military Transportation University, Tianjin 300161, China)

Considering the problem of airport emergency projection ability evaluation, the paper constructs a performance evaluation model with multi-customer closed queuing network (MCQN) and proposes specific method to treat mean value analysis (MVA) adapting to various planes and many kinds of transportation tasks, and makes theoretical calculation with this model. The comparative analysis of the calculation result and Monte Carlo simulation shows that the model reflects the performance trend of the real system, and we can find the bottleneck resource of the system and predict the influence degree of service desks’ quantity change on overall system through model analysis.

projection ability evaluation; MVA algorithm; closed queuing network; Monte Carlo simulation; sortie generation rate

2015-09-15；

2015-10-22． 作者簡介： 夏軍劍(1978—)，男，碩士，講師．

10．16807/j.cnki.12-1372/e.2016.03.017

V352

A

1674-2192(2016)03- 0075- 06