GdKP方程的最優系統和群不變解

李婷，沃維豐

(寧波大學數學系，浙江 寧波 315211)

GdKP方程的最優系統和群不變解

李婷，沃維豐

(寧波大學數學系，浙江 寧波 315211)

利用經典李群方法對GdKP方程進行Lie對稱分析，求得該方程的Lie對稱代數，及其相應的約化方程和最優系統.更進一步，作者求出了dKP方程的部分群不變解.該方法在物理中有廣泛的應用.

GdKP方程；李群方法；對稱約化；最優系統

1 引言

孤子理論的產生和發展蘊藏著一系列求解偏微分方程精確解的方法，如反散射方法、Darboux變換、Backlund變換、Lie對稱分析等等.目前，尋求非線性微分方程相似約化解的最基本有效的方法有[1]：Lie、Ovsinnio、Venikov等提出的經典李群法，Bluman和Olver等推廣的非經典李群法[23]，Clarkson和Kruskal提出的CK直接法[4]等.前兩種方法主要是基于群論，后一種方法是基于代數角度來約化方程.

本文主要考慮GdKP方程[57]

其中，f是關于u的任意函數.一方面，給出方程(1)的Lie對稱代數和約化方程，算出該5維生成元的一個最優系統[2]；另一方面，根據GdKP方程的最優系統和李代數，得到dKP方程

的部分群不變解.

2 GdKP方程的對稱和約化方程

一般地，k階微分方程F(x，u，?u，?2u，···，?ku)=0在由生成元

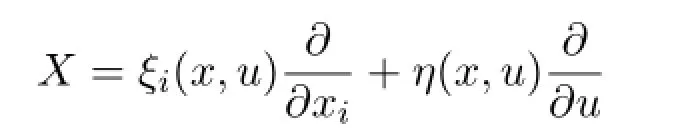
生成的群變換下是不變的，當且僅當

當F(x，u，?u，?2u，···，?ku)=0時.

設方程(1.1)滿足的點李對稱的無窮小生成元為

向量場(3)的二階延拓pr(2)X對方程(1)應用李群方法，要求它的解集S={u|△=0}在該向量場所產生的對稱群的作用下是不變的，則必須滿足下列條件：

方程(4)對任意的x，t，u，ux，ut，uxt和uxx都成立，因此通過提x，t，u，ux，ut，uxt和uxx以及他們乘積的系數，得到關于ξi(i=1，···，4)的超定方程組.求解該方程組，最后得到方程(1)的李對稱為

其中，ci(i=1，···，5)是任意常數.因此，方程(1)的對稱群的向量場為

一個微分方程的對稱群就是將方程的解仍變換為該方程的解的變換群.因此，若得到了方程的對稱群或者 Lie對稱代數，便可以用來求方程的其它解，即群不變解.取定無窮小Xi(i=1，···，5)之后，我們來求解特征方程

以得到相似變量和向量場約化形式.然后，將它們代入原方程(1)中，便可以得到相應的對稱約化方程.

2.1 X1對應的約化方程及其李對稱分析

X1對應的積分特征方程(7)為通過求解此方程，可得相似不變量和向量場約化形式u=U(ξ，η).將它們代入方程(1)并化簡，求得U(ξ，η)滿足一個2維約化方程

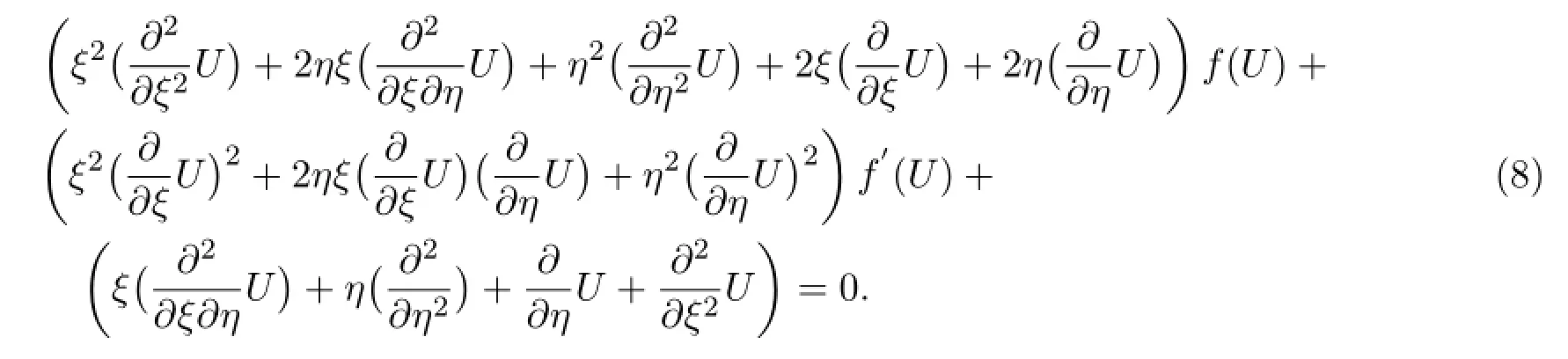
利用經典李群方法，對方程 (8)繼續進行李對稱分析，求得：方程 (8)滿足的點李對稱的無窮小生成元 v=(ξ2-2η)?ξ+ξη?η，相似不變量和向量場約化形式U(ξ，η)=F(τ)，方程就能約化成F(τ)滿足的一個常微分方程.

2.2 X2對應的約化方程及其李對稱分析

對于X2，求解方程(7)解得相似不變量是t和ξ=y2-4tx，和向量場約化形式u=U(t，ξ).將它們代入方程(1)，求得U(t，ξ)滿足一個2維約化方程

對方程 (9)繼續進行李對稱分析，求得：方程 (9)滿足的點李對稱的無窮小生成元v=c1t?t+(2c1ξ+c2t)?ξ(其中，c1和c2為任意常數)，相似不變量和向量場約化形式分別是：將它們代入方程(9)中，求得F(τ)滿足

其中，f是關于F的函數，F是關于τ的函數.

2.3 X3對應的約化方程及其李對稱分析

求解特征方程(7)給出：相似不變量x和t，和u=U(x，t).將它們代入方程(1)約化可得2維偏微分方程：

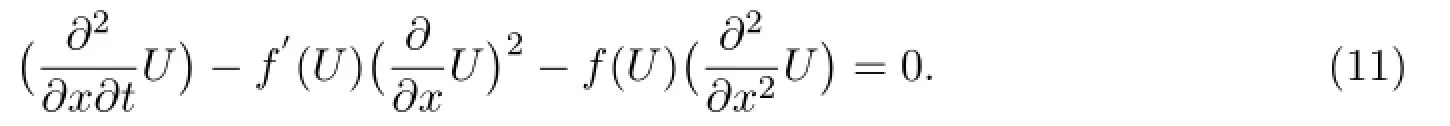
對方程(11)繼續進行李對稱分析，求得：方程(11)的對稱群的向量場為

(c1～c3為任意常數)，相似不變量向量場約化形式為 U(x，t)=F(τ).特別地，若對每一個關于ci的無窮小生成元求約化方程，可求得下列結果(見表 2.1，其中f=f(F)).

表2.1 方程(11)的約化方程

2.4 X4對應的約化方程及其李對稱分析

求解特征方程(7)得到相似不變量是x和y，和向量場約化形式u=U(x，y)，其中U(x，y)滿足一個2維約化方程：

對方程(12)繼續進行李對稱分析，求得：方程(12)的對稱群的向量場是

表2.2 方程(12)的約化方程

2.5 X5對應的約化方程及其李對稱分析

積分特征方程(7)解得相似不變量是y和t，向量場約化形式u=U(y，t).將它們代入方程(1)可以得到

進一步地，解得U(y，t)=yg1(t)+g2(t)，其中g1(t)，g2(t)均是關于t的任意函數.

3 GdKP方程的最優系統

方程(1)的無窮小對稱的李代數由(6)式生成，根據最優系統理論[816]，表3.1列出了李代數(6)的交換關系，其中表值(i，j)表示換位子[Xi，Xj].

伴隨作用由李級數給出，其中[Xi，Xj]為李代數的換位子，?為參數.表3.2給出了李代數(6)的伴隨作用，其中表值(i.j)為

表3.1 代數(6)的交換關系

表3.2 代數(6)的伴隨表示

定理3.1 代數(6)的一維優化系統由向量場

4 dKP方程的部分精確解

當GdKP方程(1)中f(u)=u時，方程(1)便化為常見的dKP方程(2).現在，利用定理3.1 GdKP方程的最優系統和李群方法，我們來求解dKP方程(2)的群不變解.要注意的是，不是所有群都能求出群不變解，群不變解的存在性準則參看文獻[17].在這里，直接列出方程(2)的部分群不變解：

[1]樓森岳，唐曉燕.非線性數學物理方法[M].北京：科學出版社，2006.

[2]Bluman G W，Kumei S.Symmetries and Differential Equations[M].New York：Springer，1989.

[3]Olver P.Applications of Lie Groups to Differential Equations[M].2nd ed.New York：Springer，1993.

[4]Clakson P A，Kruskal M D.New similarity reductions of the Boussinesq equations[J].J.Math.Phys.，1989，30：2201.

[5]Konopelchenko B，Martinez Alonso L，Ragnisco O.The-?-approach for the dispersionless KP hierarchy [J].J.Phys.A：Math.Gen.，2001，34：10209-10217.

[6]Kadomtsev B B，Petviashvili V I.On the stability of solitary waves in weakly dispersive media[J].Sov. Phys.Dokl.，1970，15：539-41.

[7]Ablowitz M J，Clarkson P A.Solitons，Nonlinear Evolution Equations and Inverse Scattering(London Math. Society Lecture Note Series vol 194)[M].Cambridge：Cambridge University Press，1991.

[8]Ramirez J，Romero J L，Tracina R.Some new solutions for the Derrida-Lebowitz-Speer-Spohnequation[J]. Com.Nonl.Sci.Num.Simu.，2013，18：2388-2397.

[9]Hu X R，Chen Y.Two-dimensional symmetry reduction of(2+1)-dimensional nonlinear Klein-Gordon equation[J].Appl.Math.Comp.，2009，215：1141-1145.

[10]Chou K S，Li G X.A note on optimal systems for the heat equation[J].J.Math.Anal.Appl.，2001，261：741-751.

[11]Chou K S，Qu C Z.Optimal systems and group classification of(1+1)-dimensional heat equation[J].Acta. Appl.Math.，2004，83：257-287.

[12]Qu C Z，Huang Q.Symmetry reductions and exact solutions of the affine heat equation[J].J.Math.Anal. Appl.，2008，346：521-530.

[13]Coggeshall S V，Meyer-ter-Vehn J.Group-invariant solutions and optimal systems for multidimensional hydrodynamics[J].J.Math.Phys.，1992，33：585-3601.

[14]Abdulwahhab M A.Optimal system and exact solutions for the generalized system of 2-dimensional Burgers equations with infinite Reynolds number[J].Com.Nonl.Sci.Num.Simu.，2015，20：98-112.

[15]Hu X R，Li Y Q，Chen Y.The construction of two-dimensional optimal systems for the invariant solutions [J].arXiv，2014，1411：3798v1.

[16]Qu C Z.Symmetries and solutions to the thin film equations[J].J.Math.Anal.Appl.，2006，317：381-397.

[17]Ovsiannikov L V.Group Analysis of Differential Equations[M].New York：Academic Press，1982.

Optimal system and group-invariant solutions for the GdKP equation

Li Ting，Wo Weifeng
(Department of Mathematics，Ningbo University，Ningbo 315211，China)

In this paper，the symmetries，similarity reductions and optimal system for the GdKP equation are studied by the classical Lie symmetry method.Furthermore，some group-invariant solutions for the dKP equation are obtained.

GdKP equation，Lie group method，similarity reductions，optimal system

O178

A

1008-5513(2016)03-0324-07

10.3969/j.issn.1008-5513.2016.03.011

2016-01-12.

國家自然科學基金(11201249)；浙江省自然基金(LY16A010002)；寧波大學科研基金(XKL14D2040).

李婷(1989-)，碩士生，研究方向：偏微分方程.

沃維豐(1981-)，博士，講師，研究方向：偏微分方程.

2010 MSC:58F07，81R25