成組不等徑直槽絲錐的優化設計及有限元分析

王曉煜，張洋 ，李榮華 ，周穎

(大連交通大學 機械工程學院，遼寧 大連 116021)*

?

成組不等徑直槽絲錐的優化設計及有限元分析

王曉煜，張洋 ，李榮華 ，周穎

(大連交通大學 機械工程學院，遼寧 大連 116021)*

對使用1 1/4-7UNC成組等徑直槽絲錐加工高硬金屬材料時會出現攻絲扭矩大，易扭斷并且加工螺紋精度低等問題.為解決這一工藝難題，在對成組絲錐攻絲受力與扭矩分析的基礎上，決定對其進行不等徑設計.以減小攻絲扭矩和提高加工螺紋精度為目標，對其幾何參數進行了優化設計.建立兩組絲錐三維實體模型，然后進行有限元分析.將兩組絲錐分析出來的結果進行對比，可以看出優化后成組不等徑直槽絲錐結構合理.并且加工出來的螺紋表面質量，精度和使用壽命均有所提高.

高硬金屬材料；成組不等徑直槽絲錐；有限元分析

0 引言

在高硬金屬材料的攻絲過程中，為減少絲錐刀齒負荷，往往采用成組絲錐攻絲，通過合理的分配切削負荷，完成攻絲加工過程[1].在使用大螺距成組等徑直槽絲錐加工高硬金屬材料時，由于材料硬度高，粗、中錐切削錐角小，切削部分長，切削厚度小，使切削變形增大，攻絲扭矩增大，絲錐易扭斷導致所加工螺紋精度低甚至工件報廢.所以在使用成組絲錐攻絲時，攻絲扭矩要小，并且每支絲錐的切削負荷要合理分配.攻絲過程中一定要注意攻絲扭矩的大小，攻絲扭矩過大會導致絲錐刀齒的斷齒或扭斷；并且在高扭矩的狀態下，會使切削溫度升高，而導致絲錐刀齒的磨損和降低絲錐的使用壽命[2].本文針對1 1/4-7UNC成組等徑直槽絲錐攻絲高硬金屬材料過程中出現攻絲扭矩大，加工螺紋精度低等問題，對其進行不等徑設計，并對其幾何參數進行優化設計.然后進行三維實體建模，通過有限元法來證明優化后絲錐的合理性.

1 成組等徑絲錐和成組不等徑絲錐

成組等徑絲錐是指每支絲錐的大徑、中徑和小徑的尺寸相同，區別僅在于切削錐角不一樣[3].粗錐錐角最小，中錐次之，精錐最大.由于采用等徑設計，每一支絲錐中徑尺寸相同，粗錐和精錐之間無區別.因此，被加工螺紋的表面質量較差，其切削圖形如圖1所示.

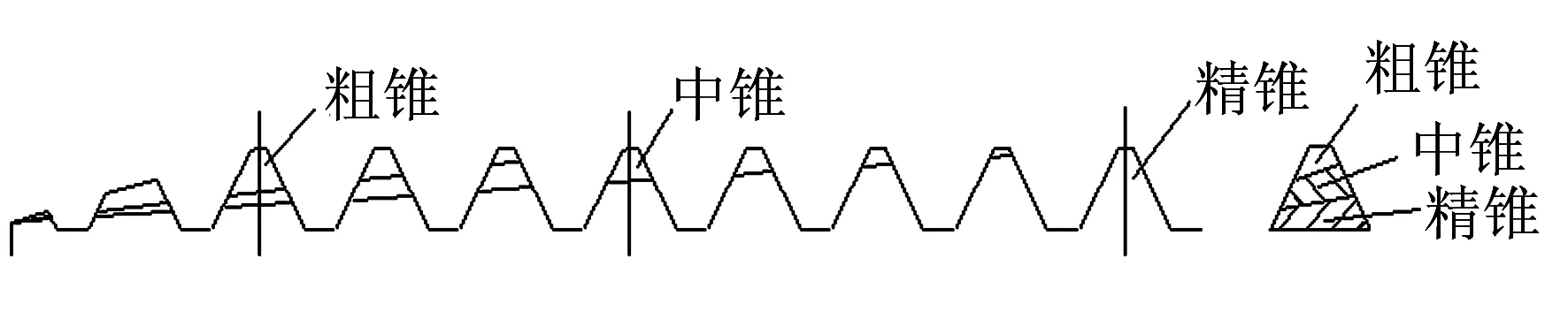
圖1 成組等徑絲錐切削圖

成組不等徑絲錐是指每支絲錐的大徑、中徑和小徑的尺寸各不相同.這種絲錐在切削時，齒頂、齒側均具一定的吃刀量，并且每支絲錐對螺紋的齒廓都具有修正的作用，不會出現重復加工造成工件表面的刮傷，所以加工螺紋表面質量好.由于切削負荷分配合理，所以絲錐的使用壽命有所提高，其切削圖形如圖2所示.

圖2 成組不等徑絲錐切削圖

2 成組絲錐攻絲受力和扭矩分析

成組絲錐每支絲錐的受力形式是一樣的，將絲錐劃分為無數個單元，以絲錐的第i個刀齒作為研究對象，按刀齒與工件間的相互作用關系.切削刃上的總切削力Fi，可以分解為主切削力分力Fc、徑向力分力Fp和軸向力分力Ff.在刀齒兩側后刀面以及主后刀面上存在著刀面與工件之間的相互擠壓產生的正壓力Ni及摩擦力Ri[4]，如圖3所示.

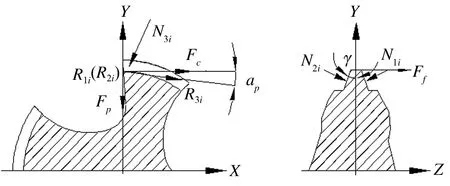
圖3 絲錐的受力狀態

絲錐攻絲扭矩一般的經驗公式表示為[5]：

式中，M為攻絲扭矩，C為被加工的材料的系數，do為絲錐大徑，P為螺距，Z為絲錐容屑槽的槽數，kr為絲錐錐角.

從攻絲扭矩公式中可以看出，在螺距和絲錐容屑槽的槽數確定后，攻絲扭矩與所加工材料、絲錐大徑和錐角有關.由于1 1/4-7UNC成組等徑直槽絲錐每支絲錐的大徑相同，而粗、中錐錐角小，切削錐長，所以攻絲扭矩大，易扭斷.而采用不等徑設計每支絲錐的大徑不同，所以可以考慮將其設計為成組不等徑直槽絲錐.以減小攻絲扭矩為目標，將每支絲錐的幾何參數進行優化設計，通過合理的分配切削負荷，從而延長絲錐的使用壽命，提高加工螺紋表面的粗糙度和精度.

3 成組不等徑直槽絲錐的優化設計

3.1 優化設計方案

成組不等徑直槽絲錐優化設計的方案是將粗、中絲錐采用等中徑設計，而每支絲錐的大徑依次增大.將精錐的中徑和大徑尺寸設計為所加工螺紋的要求.這樣，由于粗、中絲錐的大徑都有所減小，并且絲錐切削部分做短，切削錐角增大，切屑變厚，單位面積切削力減小.這樣即可以減小攻絲扭矩，又可以避免切屑過薄，造成切削刃在硬化層上摩擦而加速絲錐磨損.在切削負荷分配合理的情況下，精錐保留有一定的吃刀量，可以保證加

工螺紋精度和表面粗糙度.

3.2 成組不等徑直槽絲錐的設計

3.2.1 確定每支絲錐的負荷分配比例

在成組不等徑絲錐中，粗錐要完成攻絲過程中大部分金屬的切除，而精錐的切除量較小.所以，從絲錐的使用壽命和切削量上去考慮，以便確定每支絲錐切削負荷的分配.在成組絲錐中，當粗錐切削負荷小于40%時，粗錐切出的齒槽過淺而導致后續絲錐無法正常的導入加工，容易發生亂扣的現象.因此，粗錐的切削負荷都要按大于40%來設計.當精錐切削負荷小于8%時，精錐對粗、中錐所加工螺紋無修正作用，這將影響螺紋成品精度[6].通過上述分析，確定在絲錐的設計時采用粗錐切削面積占全部牙型面的60%，中錐占30%，精錐占10%.

3.2.2 計算每支絲錐的大徑、中徑

精錐螺紋大徑、中徑按GB968-2007《公制、美制和英制螺紋標準手冊》確定，精錐大徑為dI=31.85 mm，精錐中徑為d2I=29.47 mm.

粗錐和中錐的大徑按下式計算(dIII、dII分別為粗錐大徑和中錐大徑)：

dIII=dI-0.325P=30.67mm

dII=dI-0.108P=31.45mm

粗錐和中錐的中徑計算(d2III、d2II分別為粗錐中徑和中錐中徑)：

d2III=d2II=d2I-0.271P=28.49 mm

3.2.3 確定每支絲錐切削部分長度

由于粗錐要完成攻絲過程中大部分金屬的切除，為避免粗錐發生崩刃或者扭斷，粗錐的切削部分長度要盡可能長一些.精錐的切削量較小，為防止因切屑過薄而造成切削刃的摩損致使絲錐的加速磨損，所以精錐的切削長度盡可能短.綜合考慮后確定：粗錐切削長度取7P，中錐切削長度取4P，精錐切削長度取2P.

3.2.4 各支絲錐的錐角計算

切削部分長度L、螺紋計算高度為H與錐角φ的關系為：

經計算粗錐φ1=4.5°，中錐φ2=7.9°，精錐φ3=10.5°.

經過以上計算，得到優化后成組不等徑直槽絲錐參數，如表1所示.

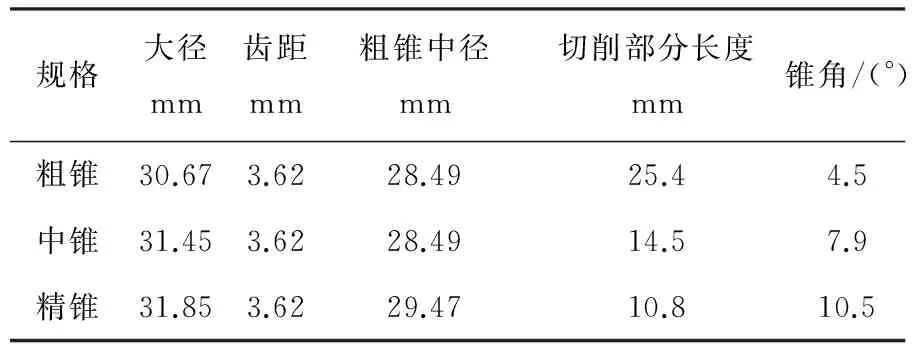
表1 優化后成組不等徑直槽絲錐參數

原成組等徑直槽絲錐參數如表2所示.

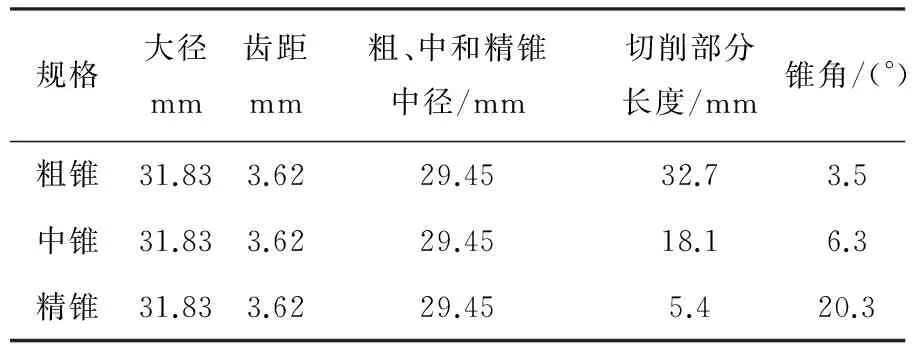
表2 原成組等徑直槽絲錐參數

3.3 優化后成組不等徑直槽絲錐與原成組等徑直槽絲錐扭矩大小對比

通過前面兩組絲錐的參數和扭矩計算公式可以算出每支絲錐扭矩的大小(扭矩單位為N·m)，經過計算，優化后成組不等徑直槽絲錐粗(212.2<246.4)、中絲錐的扭矩比原成組等徑直槽絲錐小(191.1<219.5).只有精錐扭矩稍大(182.8>173.7)，但是扭矩較小，不影響加工.所以，以上的優化設計是合理的.

4 優化后成組不等徑直槽絲錐的有限元分析

由于采用傳統設計方法無法對兩組絲錐的強度及應力應變進行精確的分析.因此，本文采用有限元法對其進行分析.由于在攻絲的過程中只有切削部分與校準部分參與切削，所以在進行絲錐的有限元分析時可以忽略絲錐柄部的影響[7].邊界條件包括模型的約束和載荷.由于在攻絲過程中所有自由度均被約束，固在模型方柄四周全部加上固定約束[8].絲錐的工作部分由切削部分和校準部分兩部分組成，切削部分磨出錐角以使切削負荷分配到幾個切削齒上.而校準部分有完整的齒形主要起引導絲錐軸向運動的作用.所以在絲錐切削部分的每個切削齒上施加所受的主切削力、軸向力和徑向力載荷，模擬絲錐切削時每齒的受力情況.由于每支絲錐所施加力的情況相同，所以只展示優化后成組不等徑直槽絲錐精錐荷施加情況,如圖4所示.

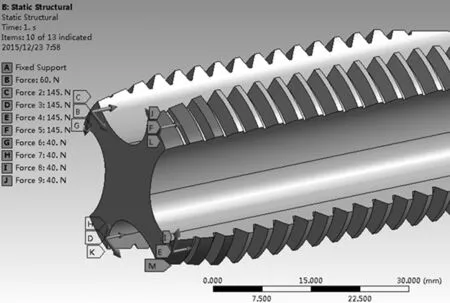
圖4 優化后成組不等徑直槽絲錐精錐載荷施加情況

對兩組絲錐進行有限元分析，可以得到兩組絲錐最大應力(應力單位為MPa)和最大應變值(應變單位為mm)的大小.經過分析，優化后成組不等徑直槽絲錐粗(10.16<12.43)、中(15.39<20.19)、精(19.67<28.67)三只絲錐的最大應力均比原成組等徑直槽絲錐要小. 優化后成組不等徑直槽絲錐粗(0.011<0.015)、中(0.027<0.06)、精(0.037<0.043)三只絲錐的最大應變也均比原成組等徑直槽絲錐小.

以上分析是將切削力合理的分配到齒面上所得到的，由于機械應力是造成絲錐損壞的主要原因，所以通過有限元方法可以驗證絲錐能否達到攻絲的要求和分析兩組絲錐實際的應力和應變分布情況.從上面的分析可以看出兩組絲錐的最大應力值均小于絲錐材料250 MPa的許用應力值.由于兩組絲錐的最大應變都非常小，所以我們只對兩組絲錐的應力進行分析.

從圖5(a)、(c)、(e)中可知，原成組等徑直槽絲錐粗、中錐的最大應力都集中在容屑槽上，最大應力值分別為12.43 MPa和20.19 MPa.原成組等徑直槽絲精錐的最大應力點在第二個切削齒處，為28.67 MPa.從圖5(b)、(d)、(f)中可知優化后成組不等徑直槽絲錐錐頭、中錐的最大應力都集中在容屑槽上，最大應力值分別為10.16 MPa和15.39MPa.優化后成組不等徑直槽絲錐精錐的最大應力點在第三個切削齒處，為19.67 MPa.

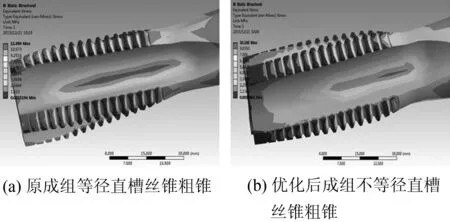
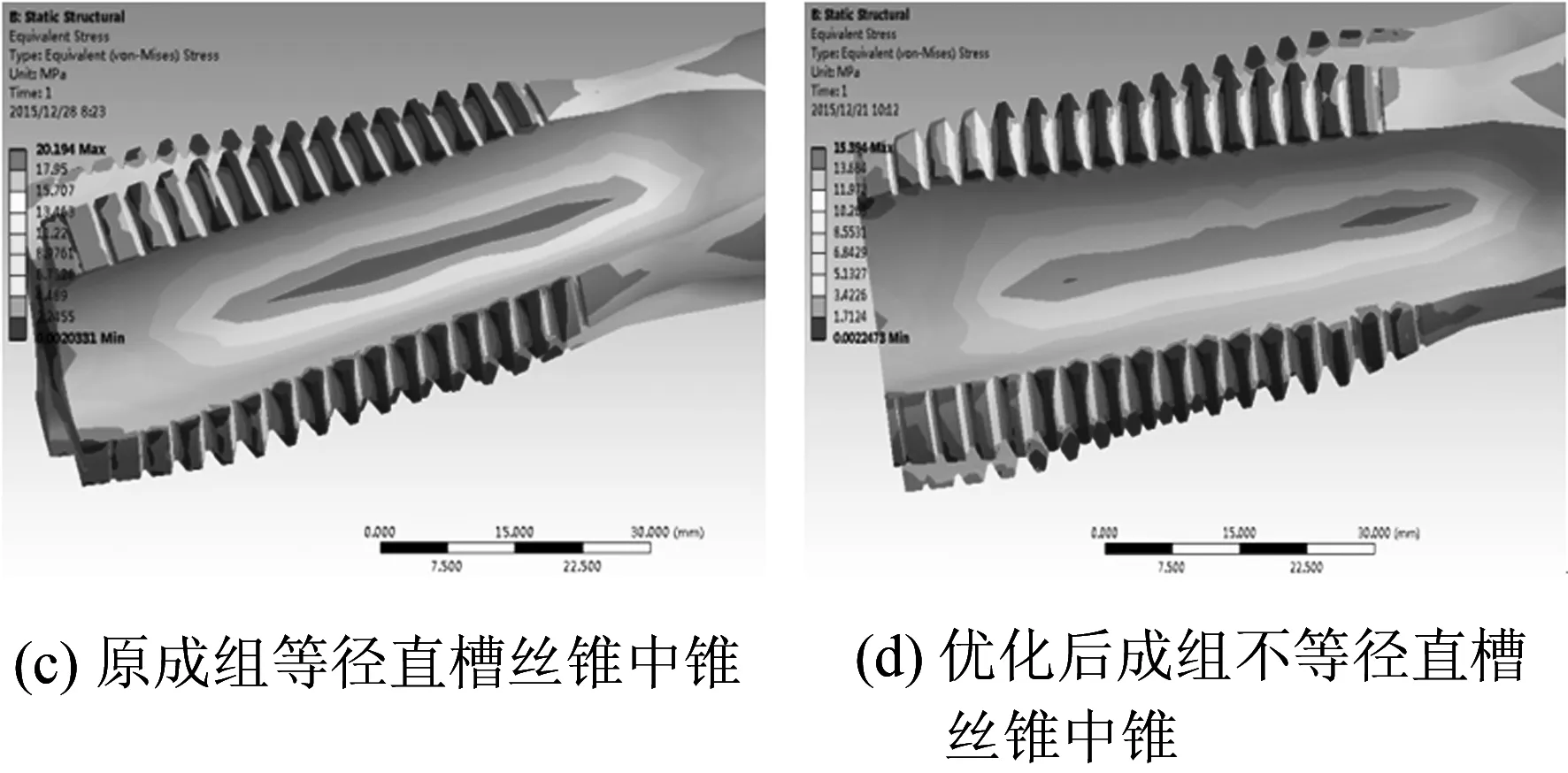
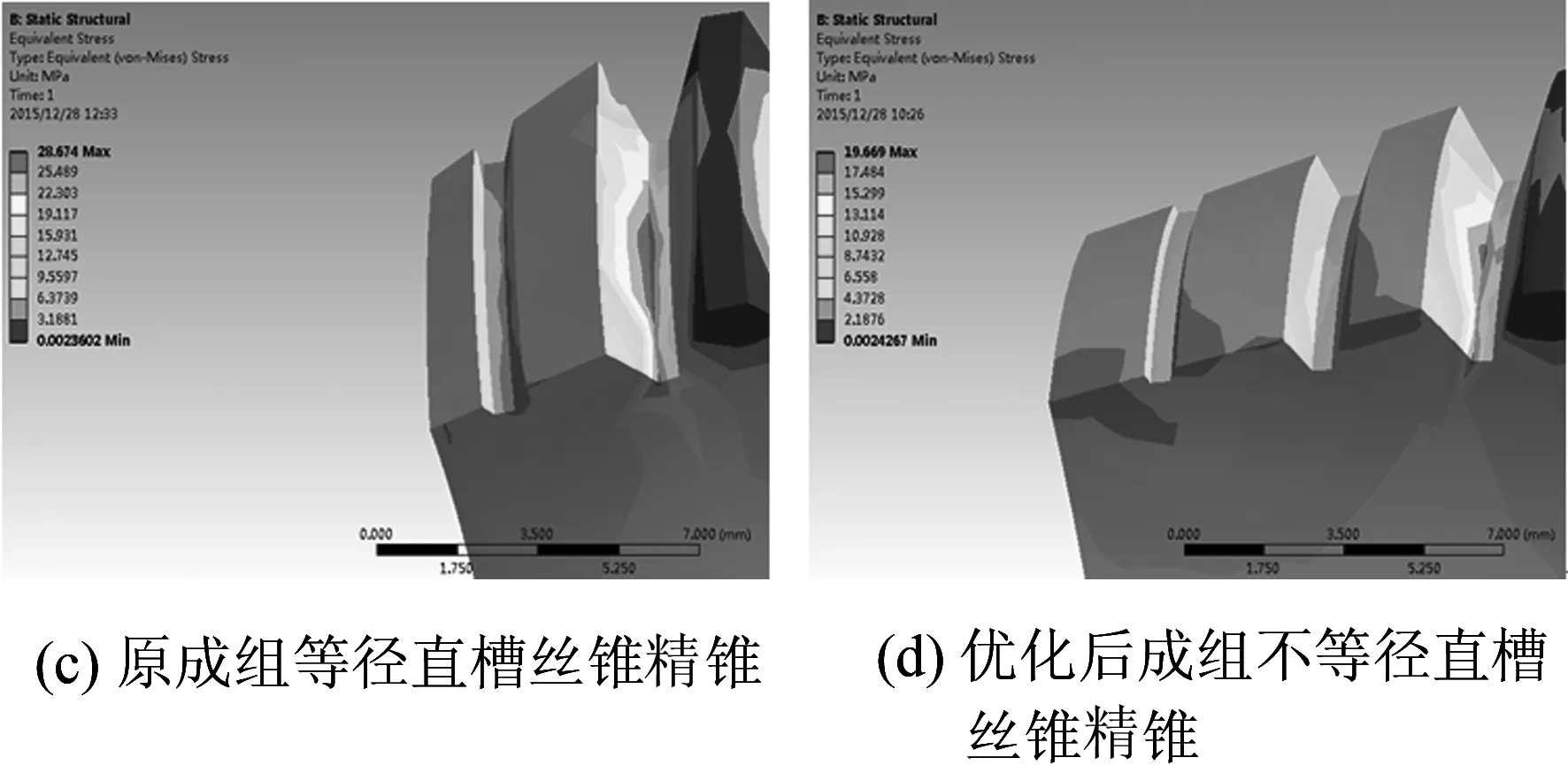
圖5 不等徑絲直槽絲錐應力云圖

原成組等徑直槽絲錐粗、中錐的最大應力都集中在容屑槽上，并且云圖所對應的色塊面積大.這是因為粗、中錐的攻絲扭矩大，絲錐容易在中間部位發生扭斷.而優化后成組不等徑直槽絲錐粗、中絲錐的最大應力也分布在容屑槽上，但應力分布均勻，云圖所對應的色塊面積較小，這就說明粗、中錐的切削負荷分配合理，扭矩較小.原成組等徑直槽絲錐精錐在切削齒上應力分布不均勻，有應力集中現象，并且應力較大.而優化后成組不等徑直槽絲錐精錐在切削齒上應力分布均勻，應力較小.應力集中是導致刀齒損壞變形的主要原因.因此，優化后成組不等徑直槽絲錐精錐滿足攻絲時的強度要求.

5 結論

通過對1 1/4-7UNC成組不等徑直槽絲錐幾何參數進行合理的優化設計，并對絲錐有限元模型進行合理的施加載荷，通過有限元軟件進行靜力分析來驗證絲錐的合理性，這種方法是切實可行的.從仿真結果中可以看出優化后成組不等徑直槽絲錐的應力的大小及其分布情況十分合理，并且加工出的螺紋表面粗糙度好，精度高，使用壽命長.

[1]程龍.典型難加工材料用修正齒絲錐槽形參數專用化研究[D]. 哈爾濱：哈爾濱工業大學，2010.

[2]韓榮第，楊榮福，李秀英.鈦合金攻絲扭矩和切削溫度的研究[J].哈爾濱工業大學學報，1985(A6)：146-153.

[3]楊鐘祺.成組不等徑絲錐設計的新方法[J].工具技術，1999(7):18-20.

[4]姚建平.整體硬質合金螺旋槽絲錐的結構分析[D].成都：西華大學，2010.

[5]金劍.大螺距螺旋槽絲錐的優化設計及有限元分析[D]. 柳州：廣西工學院，2012.

[6]徐有倉.裝配式成組不等徑內容屑絲錐的設計[J].工具技術，2010(12)：75-77.

[7]韓榮第，宋孝宗.螺旋槽絲錐的有限元分析及其結構設計[J].工具技術，2007(41)：41-43.

[8]韓榮第，桂剛.基于有限元的內容屑絲錐結構設計[J].工具技術，2006(40)：25-27.

Design Optimization and Finite Element Analysis of Unequal Serial Straight Slot Taps

WANG Xiaoyu, ZHANG Yang, LI Ronghua, ZHOU Ying

(School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116021,China)

It is hard to perform tapping processing steps using universal serial taps owing to high strength and toughness of hard metal materials. The article aims to problems such as big torque, easy to break and low accuracy of machined thread when processing hard metal materials using 1 1/4-7UNC. In order to solve the technical problem, unequal-diameter structure is designed based on force and torque analysis of serial tap tapping. To reduce the tapping torque and improve processing accuracy, the geometric parameters are better designed, and a three-dimensional model of two taps is established. The finite element analysis of the model shows that the optimized tap structure is more reasonable. Besides, the surface, accuracy and service life of the thread machined by the optimized taps are better.

hard metallic materials; unequal serial straight slot taps; finite element analysis

1673- 9590(2016)06- 0072- 04

2016-05-10

王曉煜(1979-),男，副教授，博士，從事機械電子工程的教學的研究E- mail:99925010@qq.com.

A