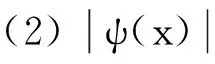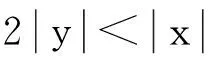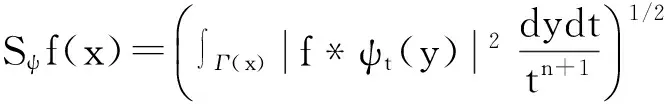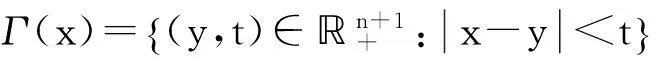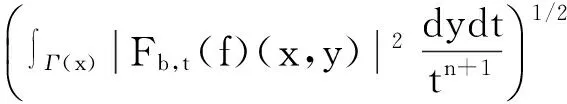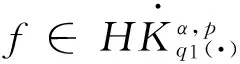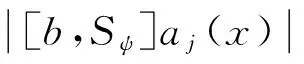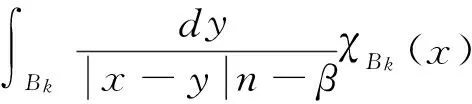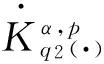Littlewood-Paley算子交換子的Lipschitz估計
王洪彬,武怡宏(淄博師范高等專科學(xué)校, 山東 淄博 255130)
?
Littlewood-Paley算子交換子的Lipschitz估計
王洪彬,武怡宏(淄博師范高等專科學(xué)校, 山東 淄博 255130)
本文應(yīng)用變指標(biāo)Herz型Hardy空間上的原子分解定理, 證明了由Littlewood-Paley算子和Lipschitz函數(shù)生成的交換子在變指標(biāo)Herz型Hardy空間上的有界性.
Littlewood-Paley算子;交換子;Herz型Hardy空間;變指標(biāo);Lipschitz估計
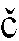
一、預(yù)備知識和記號
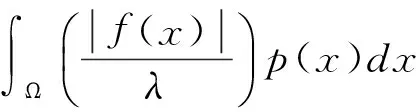
賦予如下Luxemburg-Nakano范數(shù)
‖f‖Lp(?)(Ω)=
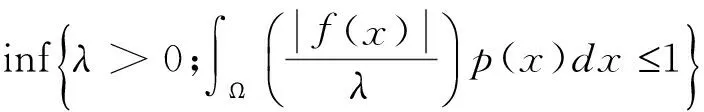
則Lp(?)(Ω)是Banach空間, 稱之為變指標(biāo)Lebesgue空間, 或者可以簡單地看作是變指標(biāo)Lp空間, 因為它們推廣了標(biāo)準(zhǔn)的Lp空間: 如果p(x)=p是常數(shù), 那么Lp(?)(Ω)與Lp(Ω)是等距同構(gòu)的. 變指標(biāo)Lp空間是Musielak-Orlicz空間的一種特殊情形.
Lipβ(n)=
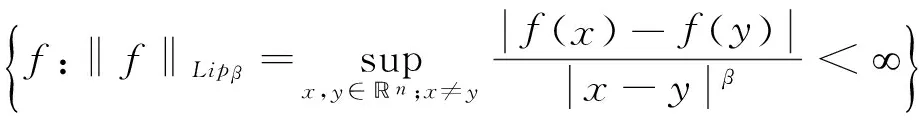
定義 1.1[5]令α∈, 0 在此基礎(chǔ)上我們給出變指標(biāo)Herz型Hardy空間的定義及其原子分解特征. 用S(n)表示n上的Schwartz空間, 它是由無窮可微且在無窮遠處迅速遞減的函數(shù)所構(gòu)成的,S'(n)表示S(n)的對偶空間. 令GNf(x)為f(x)的grand極大函數(shù), 其定義為 定義 1.2[7]令α∈, 0 定義 1.3[7]令nδ2α<, q(·)∈Ρ(n)且非負整數(shù)s≥[α-nδ2]. (2) ‖a‖Lq(·)(n). (1)' 對某個r≥1有suppa?B(0,r). 引理 1.1[7]令nδ2α<, 0 其中下確界是對f的所有上述分解而取的. 其中下確界是對f的所有上述分解而取的. 在主要結(jié)論的證明中,我們還需要下面的幾個引理. 引理 1.2[1]令p(·)∈Ρ(n). 若f∈Lp(·)(n)且g∈Lp'(·)(n), 則fg在n上可積并且 其中rp=1+1/p--1/p+. 上述不等式被稱為廣義H?lder不等式. 引理 1.3[5]令p(·)∈Β(n). 則存在正常數(shù)C使得對所有n中的球B和所有可測子集S?B, 都有 其中δ1,δ2是常數(shù)且滿足0<δ1,δ2<1(注意在整篇論文中δ1, δ2都同引理1.3中的一樣). 引理 1.4[5]設(shè)p(·)∈Β(n). 則存在常數(shù)C>0使得對所有n中的球B, 都有 給定ε>0和函數(shù)ψ滿足下面三個條件: (1)∫nψ(x)dx=0, 定義Littlewood-Paley算子為 且ψt(x)=t-nψ(x/t),t>0. 令b∈Lipβ(n), 由Littlewood-Paley算子和b生成的交換子[b,Sψ]定義為 [b,Sψ]f(x)= 其中Fb,t(f)(x,y)= ∫nψt(y-z)f(z)(b(x)-b(z))dz. 下面我們給出交換子[b,Sψ]在變指標(biāo)Herz型Hardy空間中的有界性. 定理 令b∈Lipβ(n), 0 因此, 我們得 =:I1+I2. (1) 我們首先估計I1. 由aj的消失矩條件和廣義H?lder不等式, 我們得 所以由Iβ的(Lq1(?)(n),Lq2(?)(n))有界性, 上式以及引理1.2-1.4, 我們有 ‖[b,Sψ](aj)χk‖Lq2(·)(n)C2jε+kβ-k(n+ε)‖aj‖Lq1(·)(n)‖χBj‖Lq1'(·)(n)‖χk‖Lq2(·)(n) (2) I1= (3) I1 (4) 現(xiàn)在我們來估計I2. 類似于I1, 我們可得 ‖[b,Sψ](aj)χk‖Lq2(·)(n)C2j(β-n)‖aj‖Lq1(·)(n)‖χBj‖Lq1'(·)(n)‖χk‖Lq2(·)(n) I2= (5) I2 (6) 結(jié)合(1)和(3)-(6), 我們有 因此, 定理得證. [1]Kovácik O, Rákosník J. On spaces Lp(x)and Wk,p(x)[J]. Czechoslovak Math J, 1991, 116(41): 592-618. [2]Diening L, Harjulehto P, H?st? P, et al. Lebesgue and Sobolev spaces with variableExponents[M]. Heidelberg: Springer, Lecture Notes in Math, vol. 2017, 2011. [3]Diening L, Riesz potential and Sobolev embeddings of generalized Lebesgue and Soblev spacesLp(?)and Wk, p(?)[J]. Math Nachr, 2004, 268(1), 31-43. [4]Xu J S, Variable Besov and Triebel-Lizorkin spaces[J]. Ann Acad Sci Fenn Math, 2008, 33, 511-522. [5]Izuki M, Boundedness of sublinear operators on Herz spaces with variable exponent and application to wavelet characterization[J]. Anal Math, 2010, 36(1), 33-50. [6]Nakai E, Sawano Y, Hardy spaces with variable exponents and generalized Campanato spaces[J]. J Funct Anal, 2012, 262(9), 3665-3748. [7]Wang H B, Liu Z Z, The Herz-type Hardy spaces with variable exponent and their applications[J]. Taiwanese J Math, 2012, 16(4), 1363-1389. [8]Wang H B, Liu Z Z, The wavelet characterization of Herz-type Hardy spaces with variable exponent[J]. Ann Funct Anal, 2012, 3(1): 128-141. [9]Wang H B, Liu Z Z, Some characterizations of Herz-type Hardy spaces with variable exponent[J]. Ann Funct Anal, 2015, 6(2), 224-243. [10]Wang H B, Liu Z Z, Local Herz-type Hardy spaces with variable exponent[J]. Banach J Math Anal, 2015, 9(4), 359-378. [11]王洪彬, 變指標(biāo)Herz型Hardy空間上的Marcinkiewicz積分[J]. 山東理工大學(xué)學(xué)報(自然科學(xué)版), 2015, 29(4), 16-20. [12]王洪彬, 變指標(biāo)Herz型Hardy空間上的齊性分?jǐn)?shù)次積分[J]. 魯東大學(xué)學(xué)報(自然科學(xué)版), 2015, 31(2), 107-111. [13]王洪彬, 武怡宏, 變指標(biāo)Herz型Hardy空間上的Littlewood-Paley算子[J]. 淄博師專學(xué)報, 2015, (2), 71-74. (責(zé)任編輯:胡安波) By using the atomic decomposition characterizations of Herz-type Hardy spaces with variable exponent, some boundedness of the commutators generated by Littlewood-Paley operators and Lipschitz functions on the Herz-type Hardy spaces with variable exponent is obtained. Littlewood-Paley operator;commutator;Herz-type Hardy space;variable exponent;Lipschitz estimate 2015-11-05 王洪彬(1981-)男,博士,山東淄博人,淄博師范高等專科學(xué)校數(shù)理系教師,主要從事調(diào)和分析方向研究;武怡宏(1986-)女,碩士,山東濰坊人,淄博師范高等專科學(xué)校招生就業(yè)處教師,主要從事英語教育研究。 O174.2 A (2016)02-0045-04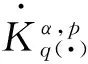
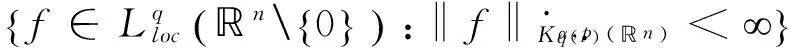
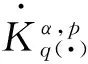
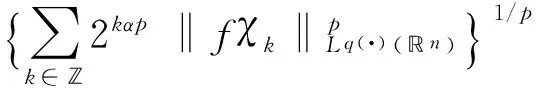
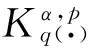
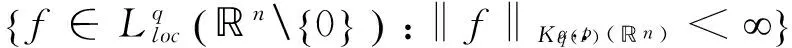
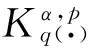
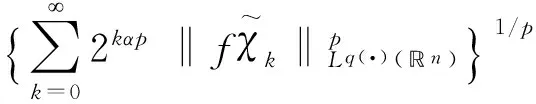
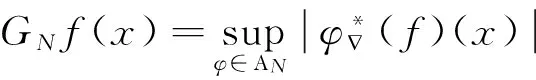

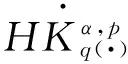
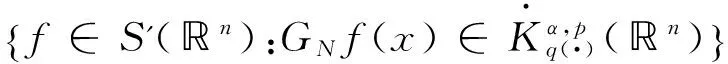
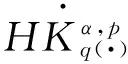
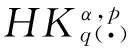
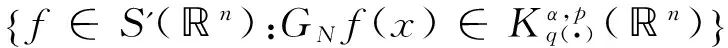
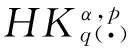
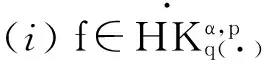
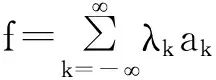
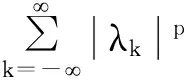
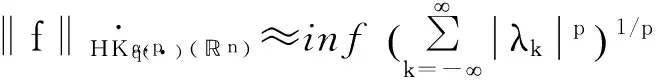
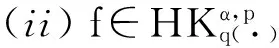
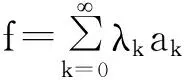
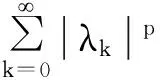
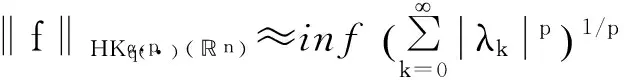
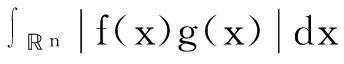
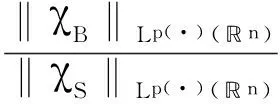
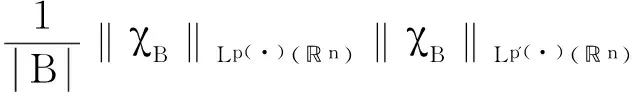
二、主要結(jié)論及證明