基于變步長梯形算法GM(1,1)模型背景值的優化

肖利哲，王學娟

（哈爾濱理工大學 管理學院，哈爾濱 150040）

基于變步長梯形算法GM(1,1)模型背景值的優化

肖利哲，王學娟

（哈爾濱理工大學 管理學院，哈爾濱 150040）

文章從GM(1,1)建模機理及背景值形成過程出發，分析出對于具有明顯指數規律的一次累加生成序列，GM(1,1)有時會出現預測誤差較大的情況，并得出背景值的構造方法是造成這種誤差的重要原因之一。利用拉格朗日插值函數和變步長梯形算法對背景值進行優化，通過對變步長梯形算法中步長大小的變化，形成了一種新的背景值構造方法，可使由背景值構成的誤差降低。

GM(1,1)模型；背景值；變步長梯形算法

0 引言

灰色系統是研究少數據、貧信息等不確定性問題的理論，灰色預測是灰色系統理論的主要研究內容之一，廣泛應用于多個領域，而GM(1,1)模型是灰色預測的核心內容[1]，長期以來受到很多學者關注，但在研究過程中發現該模型有時會出現預測精確度不高的問題，因此對該問題做了很多研究。譚冠軍[2]初步分析了GM(1,1)模型背景值構造所產生的誤差，并給出新的構造方法。王鐘羨，張怡等[3，4]根據GM(1,1)模型的指數特性，通過在定區間上求積分，給出了背景值的一個計算公式，在一定程度上提高了模型的預測精度。楊華龍等人[5]應用自動尋優定權方法，根據原始數據的模擬值與真實值之間的最小離差平方和來確定最終權重，但計算過程較為繁瑣。李俊峰，戴文戰[6]利用Newton-Cotes公式計算背景值，但n較大時，高次插值將出現Range現象，造成較大誤差。唐萬梅，向長合[7]則基于二次插值來構造背景值，該方法避免了Range現象，但預測精度難以保證。

根據以上學者的研究，本文從一次累加生成序列的指數規律角度出發，利用拉格朗日插值函數以及變步長梯形算法，對背景值進行優化，使GM(1,1)模型不僅適用于指數規律較弱的數據序列，也適用于指數規律較強數據序列。

1 GM(1,1)建模機理及誤差分析

1.1 GM(1,1)建模機理

GM(1,1)建模過程是將無規律的原始數據通過累加生成得到具有灰指數規律的數據序列，利用一階線性微分方程的指數解形式來擬合x(1)() t進行建模，將得到的數據進行累減還原，再進行預測。定義1:設原始數據則一次累加生成序列為，簡稱1-AGO，其中

由于分析的數據是離散的，為求解參數a、b，將該一階線性微分方程以定積分形式離散化，即：

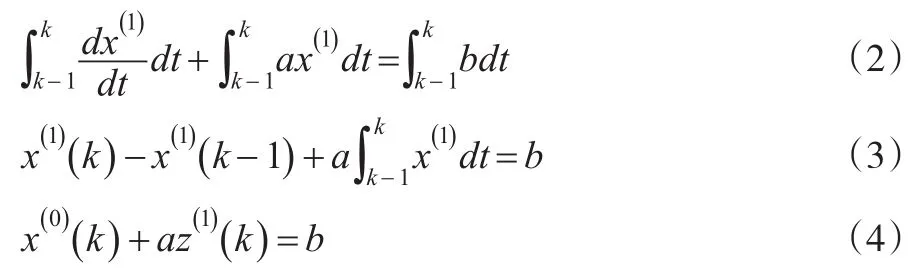
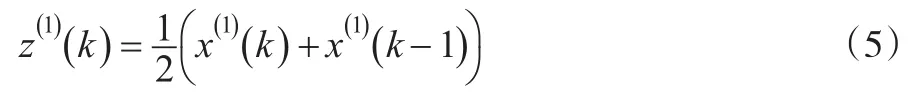
根據其離散形式，從積分幾何角度出發，求解GM(1,1)模型背景值就是求解該定積分的過程。

定理2：設x(0)，x(1)如定義1所示，若令Y和B分別為下式：

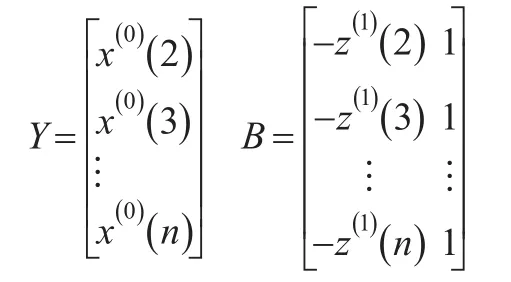
則GM(1,1)模型的最小二乘估計參數列為：

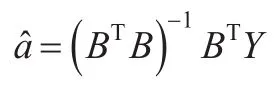
以x(o)(1)為初始值計算GM(1,1)的時間響應序列為：

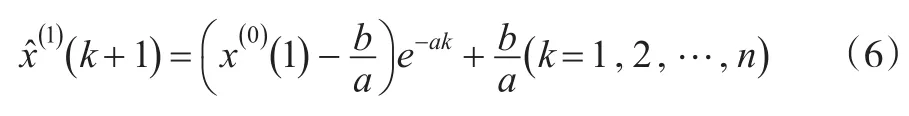
其一次累減還原值為：

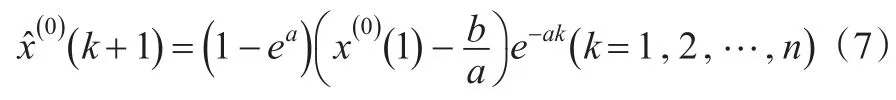
從以上的求解過程可以看出，參數a、b是影響GM(1, 1)模型預測精度的直接影響因素，而背景值z(1)(k)的構成方式又決定a、b的取值。因此科學合理的構造背景值，將有效提高模型的預測精度。

1.2 GM(1,1)模型誤差分析

2 GM(1,1)模型背景值的優化

2.1 背景值優化方法構建

根據以上誤差來源分析，針對1-AGO指數規律較強的數據序列，從背景值形成的積分幾何意義出發，在積分區間[k -1，k]上插入適當的點，此處采用拉格朗日函數進行插值，近似得到x(1)(t)在插值點處函數值。并結合變步長梯形算法，通過選取合適的步長，即在對每個積分區間進行m等分時，選取合適的m值，用m個小梯形面積之和來近似代替曲邊梯形面積。以小區間向下凹為例說明，如圖1所示。

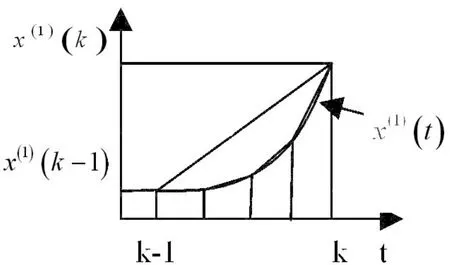
圖1 面積逼近示意圖

若函數 y=f(x)在[a ，b]上有定義，m+1個節點a=x0＜…＜xm=b處的值已知，則Lm(xj)=yj(j=0，1，…，m)。

則稱此m+1個多項式l0(x)，l1(x)，…，lm(x)為節點x0＜…＜xm的m次插值基函數。可得m次插值基函數為：

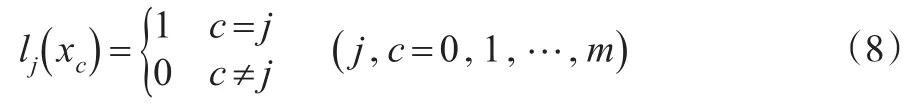
因此滿足式⑻的插值多項式Lm(x)可表示為：

式⑼稱為拉格朗日插值函數，簡稱Lm。

定義3：設將[ ] a，b分為m等分，共有m+1個節點，如果將求積區間再二分一次，則分點增至2m+1個，而每個子區間[ ] xd，xd+1經過二分只增加一個分點，即xd+1)，其中xd=a+ih;i=0，1，…，m;使用復化梯形公式求得該子區間上的積分值為：

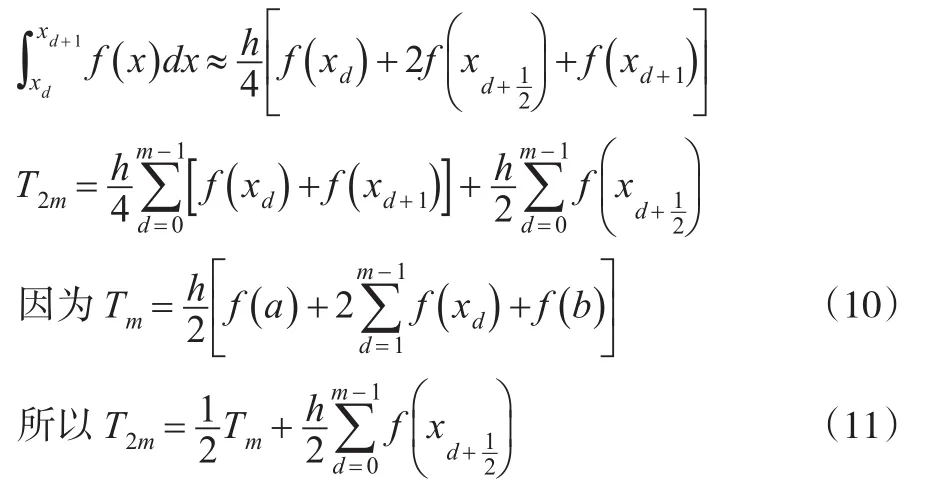
式（11）給出了Tm與T2m之間的遞推關系，方便計算機編程，減少了計算量，由此可見變步長梯形算法為復化梯形公式的逐次分半算法，下面討論如何確定等分數m。

本文通過m計算背景值 z(1)(k )，以z(1)(k)確定a、b以得到擬合函數由與x(0)(k)計算相對誤差ε(k)及平均相對誤差。m在變化過程中使z(1)(k)、ε(k)、ˉ依次變化，最終使在變化過程中達到最小，選擇此時m。

根據1-AGO波動性，由這些點擬合的Lm呈現凹凸變化的趨勢，如圖2所示。在對小區間進行等距劃分并插值時，不能使每個小區間上的m個小梯形面積之和都更接近定積分值，相應的利用重構的z(1)(k)建模預測，不能使每個ε(k)都降低，進而使εˉ隨ε(k)變化程度而改變。

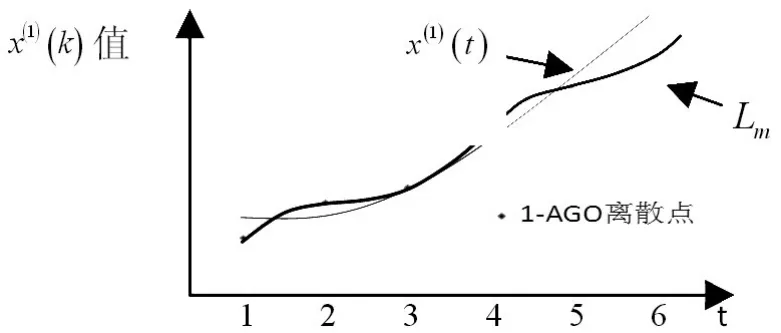
圖2 曲線擬合圖

②若且選擇m=m1時計算背景值。

③若則繼續增大m，直至某個m值，設為m*，若繼續增大m，則ˉ增大。以m*計算背景值。

當原始數據為非波動性數據序列且1-AGO指數規律越明顯時，則Lm整體向下凹或向上凸，可使Lm與x(1)(t)變化趨勢更接近，則εˉ可降低的空間就越大。

下面以實證部分數據說明z(1)(k)、ε(k)、ˉ之間變化關系。

如表1所示，隨m增大z(1)(k)均在減小，相應的ε(2)增大，ε(3)，ε(6)減小，ε(4)，ε(5)先減小后增大，且ˉ逐漸減小，當m=8時ˉ達到最小，以此m對應的z(1)(k)計算參數a、b。

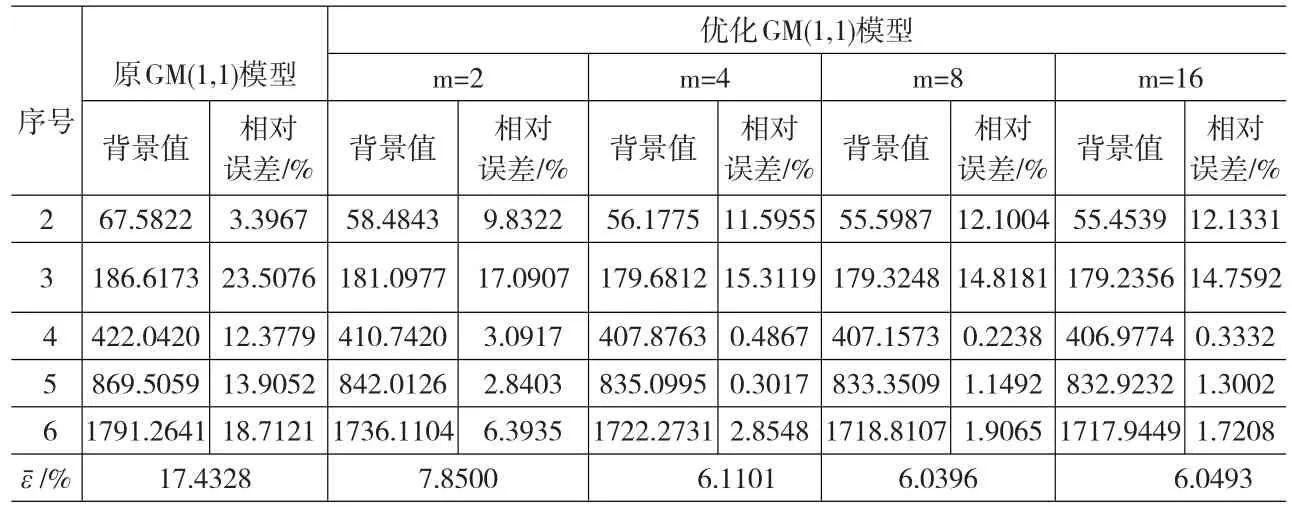
表1 背景值與相對誤差及平均相對誤差變化對照

2.2 基于優化背景值的GM(1,1)模型的改進

⑴計算ρ(k)與σ(k)分析指數規律，并利用軟件計算原模型平均相對誤差設定初始值m1，由Lm函數計算區間[k ，k+1]上m1等分點處的函數值。

⑵根據變步長梯形算法，由m1值及插值點處的函數值計算背景值。

⑶根據定理2計算參數a、b的值，并根據式⑺求得原始數據的模擬值。

⑷計算模擬值的相對誤差ε1(k)及整體平均相對誤差

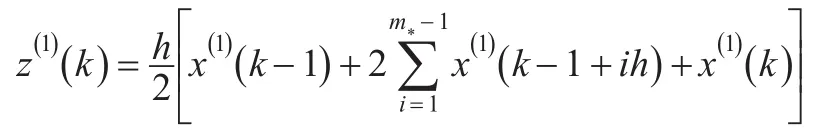
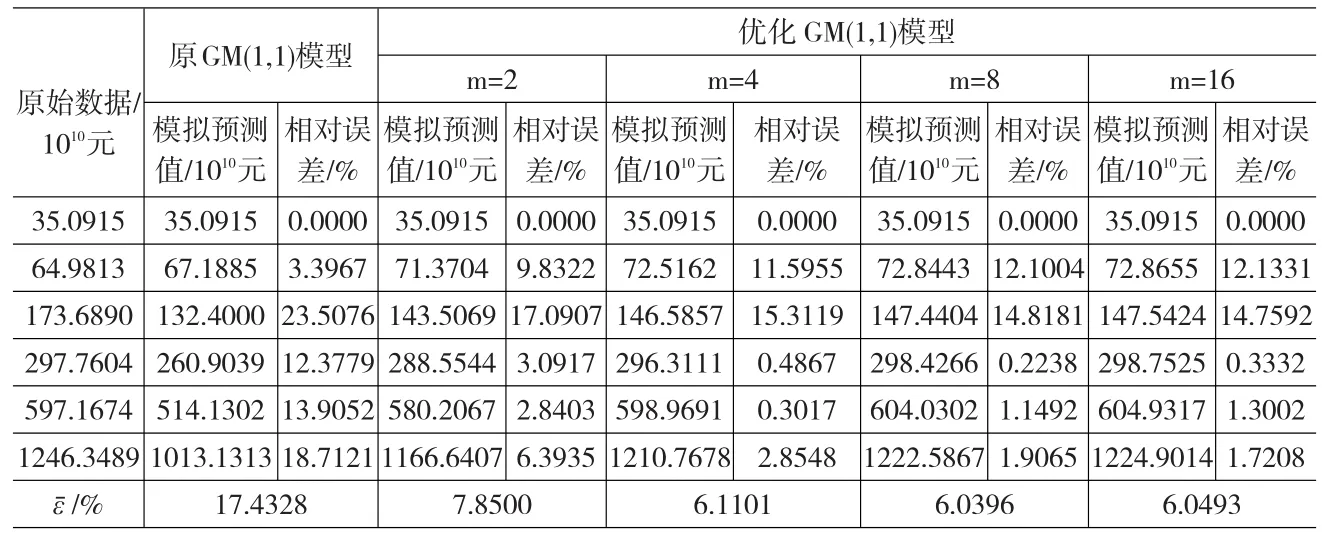
表2 原模型與優化模型工業總產值模擬預測比較

3 實例分析

本文以上海市六五至十一五期間工業總產值作為基本數據說明模型改進情況，原始數據見表2所示。

⑴分別計算ρ(k )與σ(1)(k)的值，得出其1-AGO具有較強的指數規律。并計算原模型平均相對誤差，見表2。

⑵令初值m=2，插入一個點，并以區間[1 ，2]為例計算插值及背景值，其他區間類似。給出Lm函數：

L6(x)=0.1406x5+4.4821x4-51.1969x3+236.5319x2-357.8253x+202.9591

⑶計算背景值

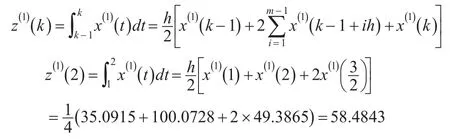
同理計算z(1)(k)，k=3，4，5，6時的值，見表1。將得到的背景值帶入到GM(1,1)模型，得到m=2時模擬預測值，并分別取m=4、8、16,計算不同m值時的背景值，并代入GM (1,1)模型計算模擬值，與原模型進行比較，見表2。

如表2所示，當m取8時模型的平均相對誤差最小，選擇m*=8時的背景值計算a、b，并利用式⑺進行預測。

GM(1,1)模型有三種檢驗方法：殘差檢驗、關聯度檢驗以及均方差比檢驗，本文采用均方差比檢驗方法，如下:

設原始數據序列x(0)及殘差序列的均值和方差分別為：

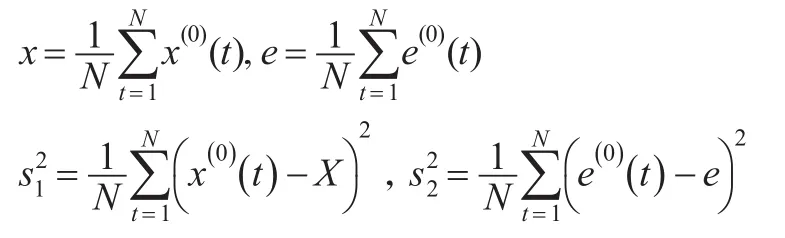
模型的精度由P和c共同描述，一般分為四個等級，一級：0.95≤p，c≤0.35；二級：0.80≤p＜0.95，0.3＜c≤0.5；三級：0.70≤p＜0.80，0.5＜c≤0.65；四級：P＜0.70，0.65＜c。對模型的精度進行檢驗，經過計算得到 p=1，c=0.01。該模擬預測的精度屬于一級，精度較高。

4 總結

本文針對一次累加生成指數規律明顯的數據序列，利用拉格朗日插值函數以及變步長梯形算法，提出了新的背景值構造方法。在變步長梯形算法中，隨著步長的變化，也就是等分數m取值的不同，預測結果的平均相對誤差會隨之變化。變化過程中會有一個m*使平均相對誤差達到最小或其差值小于某一特定值，以m*計算模型背景值。若m*=0則使用原模型，若m*＞0表示優化了GM(1,1)模型，提高了模型的預測精度。通常，當1-AGO指數規律越明顯時，m*應越大，隨指數規律的減弱m*變小，當m*=0時，即使用原模型。根據重構背景值的GM(1,1)模型，利用上海市六五至十一五期間工業生產總值進行模擬預測，證明該優化模型可以提高指數規律較強的1-AGO的預測精度，并具有一定的理論意義與應用價值。

[1]劉思峰，黨耀國.灰色系統理論及其應用[M].北京：科學出版社，2010.

[2]譚冠軍.GM(1,1)模型的背景值構造方法和應用(Ⅰ)[J].系統工程理論與實踐，2000，(4).

[3]王鐘羨，吳春篤.GM(1,1)改進模型及其應用[J].數學的實踐與認識，2003，33(9).

[4]張怡,魏勇,熊常偉.灰色模型GM(1,1)的一種新優化方法[J].系統工程理論與實踐，2007，(4).

[5]楊華龍，劉金霞，鄭斌.灰色預測GM(1,1)模型的改進及應用[J].數學的實踐與認識，2011，41(23).

[6]李俊峰，戴文戰.基于插值和Newton-Cores公式的GM(1,1)模型的背景值構造新方法與應用[J].系統工程理論與實踐，2004，(10).

[7]唐萬梅，向長合.基于二次插值的GM(1,1)模型預測方法的改進[J].中國管理科學，2006，14(6).

（責任編輯/易永生）

N941.5

A

1002-6487（2016）23-0008-04

黑龍江省高教綜合改革試點專項課題資助（JG2013010288）

肖利哲（1961—），男，黑龍江哈爾濱人，碩士，教授，研究方向：統計學、人力資源。

王學娟（1989—），女，河北廊坊人，碩士研究生，研究方向：人力資源管理。