GNSS+SINS組合導航地固系高度阻尼算法
丁磊香,許厚澤,王 勇,柴 華,蔡小波
(1. 河南城建學院,河南 平頂山 467036; 2. 中國科學院測量與地球物理研究所大地測量學與地球動力學國家重點實驗室,湖北 武漢 430077)
?
GNSS+SINS組合導航地固系高度阻尼算法
丁磊香1,2,許厚澤2,王 勇2,柴 華2,蔡小波2
(1. 河南城建學院,河南 平頂山 467036; 2. 中國科學院測量與地球物理研究所大地測量學與地球動力學國家重點實驗室,湖北 武漢 430077)
GNSS+SINS組合導航在地固系中計算有諸多優點,但GNSS信號缺失時的高度阻尼比較復雜。本文從空間直角坐標系與大地坐標系的關系出發,結合地固系捷聯慣導的導航方程,提出了一種地固系高度阻尼算法。經仿真測試證明,應用此算法在地固系高度阻尼,可以達到與導航系相同的效果,證明了算法的有效性。
地固系;GNSS+SINS組合導航;高度阻尼;導航系
相比導航系,全球衛星導航系統+捷聯慣導系統(GNSS+SINS)組合導航在地固系(ECEF)中計算,編排效率提高約40%,Kalman濾波效率提高約10%,在地固系中的計算比導航系計算綜合效率提高約30%[1-2]。另外,在GNSS+SINS組合導航中,GNSS的數據處理是在地固系進行的,選取地固系作為SINS的計算坐標系無需GNSS導航結果的轉換[3],地固系特別適合于GNSS+SINS組合應用領域[2]。針對SINS在地固系中的計算,文獻[4—5]作了有益的研究。
但GNSS+SINS組合導航在地固系計算同樣存在不足,相比導航系,高度阻尼復雜。當GNSS信號較好時,是不需要高度阻尼的,但當信號被遮擋時間較長時,高度通道是發散的,此時需要高度阻尼。相比導航系中的僅在高度通道增加阻尼的處理,由于慣導高度通道發散將影響到地固系的3個坐標值,地固系的阻尼算法將更為復雜。針對此問題,本文從空間直角坐標系與大地坐標系的關系出發,結合地固系捷聯慣導的導航方程,提出一種地固系高度阻尼算法。經仿真測試證明,應用此算法在地固系高度阻尼,可以達到與導航系相同的效果,證明算法的有效性。
一、導航方程
1. 坐標系定義
1) 地固系(e系):原點在地球質心,x軸指向格林尼治平均子午圈,y軸與x、z軸正交,z軸平行于地球自轉軸。
2) 當地水平坐標系又稱導航系(n系):原點在載體中心,x軸沿卯酉圈指向東,y軸沿子午圈指向北,z軸橢球外法線指向天頂。
3) 載體系(b系):原點在載體中心,x軸指向載體的右方,y軸指向載體的前方,z軸指向載體上方。
2. 地固系導航方程
捷聯慣導系統在不同的坐標系有不同的導航方程,由于GNSS+SINS組合導航在地固系計算中有諸多優點,GNSS+SINS組合導航通常在地固系中計算,在此直接給出地固系導航方程[3]
(1)
式中,r、v、C分別為位置、速度與轉換矩陣,上下標的含義同文獻[2]。
依據導航方程可以求出速度和位置
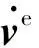
(2)
re(t+Δt)=re(t)+(ve(t+Δt)+ve(t))Δt/2
(3)
二、空間直角坐標系與大地坐標系的相互轉換
由大地坐標系向直角坐標系轉換有嚴密的計算公式,在此直接給出
(4)
式中,B、L、H分別為大地緯度、大地經度與大地高;N、e分別為參考橢球卯酉圈曲率半徑與第一偏心率;(xe,ye,ze)為地固系直角坐標。
由直角坐標轉換經緯度有許多不同解法[6-10],一般分為3類:封閉解法、迭代法、近似算法,工程應用一般使用近似算法。本文推薦使用文獻[9]的近似算法,該計算方法既簡單,又有很高的計算精度,緯度的計算精度優于10-12(10-7角秒)[11],可以滿足需求,詳細的計算公式如下
(5)
式中,a為參考橢球的長半軸;b為橢球的短半軸;e′為橢球的第二偏心率;其余符號含義與式(4)相同。
三、地固系高度阻尼算法
在導航系高度阻尼比較容易實現,直接引入慣性指示高度Hn與外部觀測高度Ha之間差值(Ha-Hn)的負反饋,即用外部觀測高度代替慣性指示高度。
要想實現地固系高度阻尼,首先需要把高度從地固系3個直角坐標解耦分離,具體做法是根據式(5)把地固系直角坐標轉換為大地坐標,記為(Bn,Ln,Hn),得到GNSS+SINS導航高度與導航經緯度,當GNSS信號被遮擋時,導航高度也稱為慣性指示高度;然后借鑒導航系的高度阻尼方法,直接用外部觀測高度代替慣性指示高度,得到阻尼后的大地坐標(Bn,Ln,Ha);最后把大地坐標轉換為地固系直角坐標,完成高度阻尼。阻尼后的地固系直角坐標可寫為
(6)
關于外部觀測高度的選擇,如果有引入其他系統提供高度信息(氣壓高度或無線電高度信息等),直接應用即可。但GNSS+SINS組合導航通常沒有此類信息,因此可以借鑒純慣導對高度阻尼的做法,在GNSS信號缺失時,把外部觀測高度設為常值,這個常值可為GNSS信號較好時確定的高度值。
四、仿真驗證
為了驗證算法的有效性,對該算法進行了仿真,并與導航系高度阻尼結果進行比較,用來驗證算法的有效性。仿真條件如下:陀螺零漂0.01°/h,加表零偏10-4g(g為重力加速度),載體沿赤道以10 m/s勻速直線運動,比較地固系與導航系24 h的高度阻尼下的導航位置誤差,結果如圖1、圖2所示。

圖1 地固系高度阻尼下的經緯度誤差
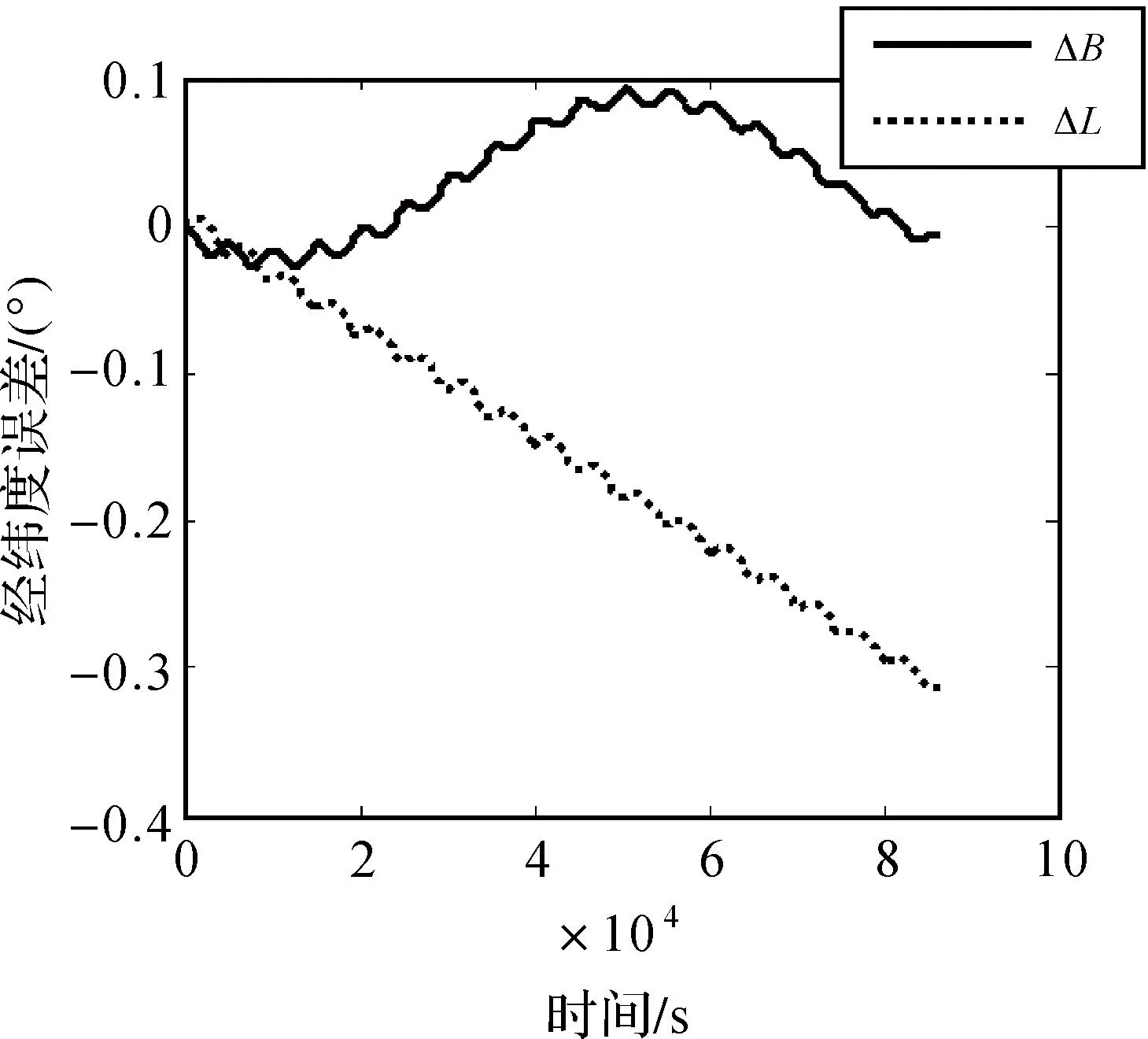
圖2 導航系高度阻尼下的經緯度誤差
比較圖1與圖2可以看出,地固系與導航系的經緯度誤差幾乎相同,其差異可以忽略;經緯度誤差呈現明顯的舒拉震蕩,緯度誤差存在24 h震蕩的趨勢,經度誤差存在無界增長的趨勢,誤差趨勢和導航系相同,證明地固系的高度阻尼算法是有效的。
五、結束語
針對GNSS+SINS組合導航GNSS信號缺失時間較長時的高度阻尼,本文從空間直角坐標系與大地坐標系的關系出發,結合地固系捷聯慣導的導航方程,提出了一種地固系高度阻尼算法,并與導航系進行了比較。結果表明,阻尼后的位置誤差完全相同,證明了算法的有效性。
[1] WEI M, SCHWARZ K P. A Strapdown Inertial Algorithm Using an Earth-fixed Cartesian Frame[J]. Navigation, 1990, 37(2): 153-167.
[2] 董緒榮, 張守信, 華仲春. GPS/INS組合導航定位及其應用[M]. 長沙:國防科技大學出版社, 1998:78-120.
[3] 柴艷菊. 挖掘信息提高GPS/INS導航精度和理論與方法研究[D]. 武漢: 中國科學院測量與地球物理研究所, 2008:16-18.
[4] 柴華, 王勇, 許大欣, 等. 地固系下四元數和卡爾曼濾波方法的慣導初始精對準研究[J]. 武漢大學學報(信息科學版), 2012, 37(1):68-72.
[5] 張秋昭, 張書畢, 王堅, 等. 露天礦卡車低成本GPS/INS組合導航系統動態對準模型[J]. 煤炭學報, 2013, 38(8):1362-1367.
[6] TURNER J D. A Non-iterative and Non-singular Perturbation Solution for Transforming Cartesian to Geodetic Coordinates[J].Journal of Geodesy,2009,83(2):139-145.
[7] JONES G C. New Solutions for the Geodetic Coordinate Transformation[J]. Journal of Geodesy, 2002, 76(8): 437-446.
[8] VERMEILLE H. Computing Geodetic Coordinates from Geocentric Coordinates[J]. Journal of Geodesy, 2004, 78(1/2): 94-95.
[9] BOWRING B R. The Accuracy of Geodetic Latitude and Height Equations[J]. Survey Review, 1985, 28(218): 202-206.
[10] 桑金. 空間大地直角坐標與大地坐標反算的非迭代法[J]. 測繪通報, 2000(5): 37,39.
[11] 黃謨濤, 翟國君, 管錚, 等. 空間直角坐標和大地坐標的轉換[J]. 解放軍測繪學院學報, 1998, 15(3): 164-168.
Altitude-damping Algorithm of GNSS+SINS Integrated Navigation under ECEF Frame
DING Leixiang,XU Houze,WANG Yong,CHAI Hua,CAI Xiaobo
2016-01-29;
2016-07-01
國家自然科學基金(41274084;41074001;41374086)
丁磊香(1982—),男,博士,研究方向為GNSS+INS組合導航理論及應用。E-mail: dingleixiang@163.com
丁磊香,許厚澤,王勇,等.GNSS+SINS組合導航地固系高度阻尼算法[J].測繪通報,2016(11):12-14.
10.13474/j.cnki.11-2246.2016.0354.
P228
B
0494-0911(2016)11-0012-03

