云南省測繪成果向2000國家大地坐標系轉換的方法

周峻松，李石華,，李文華，彭雙云

(1. 云南省基礎地理信息中心，云南 昆明 650034； 2. 云南師范大學旅游與地理科學學院，云南 昆明 650500)

?

云南省測繪成果向2000國家大地坐標系轉換的方法

周峻松1，李石華1,2，李文華1，彭雙云2

(1. 云南省基礎地理信息中心，云南 昆明 650034； 2. 云南師范大學旅游與地理科學學院，云南 昆明 650500)

以國家測繪地理信息局對2000國家大地坐標系(CGCS2000)推廣使用的要求為指導，根據坐標系建立的原理，結合云南省現有測繪成果實際，利用布爾莎七參數模型和柵格模型法，開展了云南省省級基礎測繪成果由1954北京坐標系、1980西安坐標系向2000國家大地坐標系轉換方法研究。結果表明：①兩種方法的殘差中誤差均在其反轉時的殘余誤差范圍內，證明了七參數法和柵格模型法是可靠的；②從對兩種方法的檢驗結果來看，模型法比柵格法的改算點位殘差小；③柵格模型改正法可用于高精度要求的坐標改算，而七參數法可用于對精度要求不高或需要保持舊成果整體精度的坐標轉換。

1954北京坐標系；1980西安坐標系；2000國家大地坐標系；坐標轉換；布爾莎模型；柵格模型

此前，關于啟用2000國家大地坐標系(CGCS2000)的提議已獲國務院批準，國家測繪地理信息局規定：自2008年7月1日啟用CGCS2000，并用8～10年的時間完成現行國家大地坐標系向CGCS2000的過渡和轉換。國家測繪地理信息局提供了CGCS2000的技術參數，并對新舊坐標系的轉換和使用作出了說明。由于1980西安坐標系已采用20多年，大量的測繪成果都采用的是1980西安坐標系，甚至是1954北京坐標系[1]，因此面臨著大量的坐標轉換問題。眾多學者就其轉換方法開展了深入研究與試驗[2-5]，其研究思路與方法可為后續研究提供借鑒與參考。

根據國家測繪地理信息局《關于加快2000國家大地坐標系推廣使用的通知》(國測國發〔2013〕11號)的要求，尚未開展此項工作的省份，應盡快完成各自省份地理信息成果的梳理、省級成果轉換，推動市縣級成果轉換。為此，云南省測繪地理信息局將該項工作作為2014年度基礎測繪任務之一，由云南省基礎地理信息中心承擔并完成“云南省基礎測繪成果2000國家大地坐標系轉換”任務。本文分析了現有坐標系轉換方法，在調研其他省份的工作經驗與充分分析相關文獻研究結論的基礎上，結合本省基礎測繪成果和地域實際，有必要就省級測繪成果坐標系轉換方法展開研究，以期為1954北京坐標系、1980西安坐標系向CGCS2000轉換方法提供案例。

一、資料利用與轉換方法

1. 資料利用

本研究中充分利用了國家、省級、地方現有的測繪成果。具體包括：

1) 云南省內的天文大地網與高精度GPS2000網聯合平差地面網點CGCS2000成果2168個點，但經過與現有的舊成果進行人工比對、檢核和甄別，預選2100個點作為公共已知點使用。

2) 為改善已知點的圖形分布結構、提高轉換精度，從西安大地數據處理中心補充收集到省外周邊428個點CGCS2000坐標系成果、省內68個點1980西安坐標系與1954北京坐標系的成果。經過與現有的成果比對，將343個點(省內68個點、省外275個點)作為預選公共已知點使用。

3) 似大地水準面精化成果(CGCS2000坐標系)，獲取高程異常值，將正常高換算為CGCS2000坐標系大地高。

4) 利用《1980西安大地坐標系統成果圖集》，采集其中的1954北京坐標系、1980西安坐標系高程異常圖等值線，用于高程異常值空間分布的內插，獲取高程異常值。

5) 國家測繪地理信息局提供的“1980西安坐標系到CGCS2000坐標系空間格網改正量”，主要用于結果比較及檢驗。

6) 云南省1980西安坐標系、2000國家大地坐標系兩套成果的GPS B級點31個點、GPS C級點1311個點，作為結果的檢驗。

7) 以似大地水準面精化工作時聯測轉換的成果40個點作為結果檢驗。

8) 利用少量國家Ⅱ等點的控制成果。聯測了安寧、玉溪交接區域的高魯山Ⅱ、雞背山Ⅱ、大黑山(二)Ⅱ，對送鬼山ⅢⅡ進行了聯測檢驗工作。

2. 轉換方法

利用布爾莎模型系統轉換后，在已知點上還有殘留誤差，且各已知點的模型誤差表現出明顯的區域差異性。而這種區域差異性期望用一種二維空間場模型來描述，常用的場模型有6種(如圖1所示)。

圖1 二維空間場模型

這些場模型的核心是利用已知點進行空間插值。空間內插可分為幾何方法、統計方法、空間統計方法、函數方法、隨機模擬方法、物理模型模擬方法和綜合方法[6]。其中幾何方法主要是基于“地理學第一定律”的基本假設[7]，即鄰近的區域比距離遠的區域更相似。最常用的幾何方法有泰森多邊形(最近距離法)和反距離加權方法。反距離加權法是最常用的空間內插方法之一，認為與未采樣點距離最近的若干個點對未采樣點值的貢獻最大，其貢獻與距離成反比可表示為

(1)

式中，Z為待插值的柵格點；Zi為第i個已知點的改正值；di為擬合點到第i個已知點的大圓距離；n為用于擬合插值的已知點的數目。

用該方法計算出每一個點空間分布的模型殘差改正值，最后形成兩個二維分量上的改正量柵格集，在本研究中將其定義為柵格改正法。

移動擬合法的計算模型中，其定權用的是空間直線距離d，而在實際操作時用的是地理坐標，其計算的距離與空間直線距離有一定差異。但由于其作用范圍只是附近的點，比較地理坐標距離計算的權值與空間直線距離計算的權值發現，其權值的比重基本一致，而計算工作量得到大大簡化，故用地理坐標代替計算。

二、計算過程與結果分析

1. 布爾莎模型七參數解算

在求解七參數時，先將大地坐標轉換到空間直角坐標系下，再求解七參數，流程如圖2所示。

圖2 計算流程

(1) 大地坐標與空間直角坐標系之間的轉換

大地坐標(B、L、H)轉換為空間直角坐標(X、Y、Z)的公式為

(2)

空間直角坐標(X、Y、Z)轉換為大地坐標(B、L、H)的公式為

(3)

式(3)用迭代法計算。

(2) 七參數轉換

七參數轉換模型采用布爾莎模型，它在兩空間直角坐標系之間存在嚴密的轉換關系，其形式非常簡單，物理意義也非常明晰，即

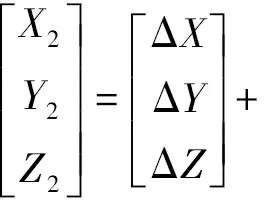
(4)

式中，(X1，Y1，Z1)為原坐標系下三維坐標；(X2，Y2，Z2)為新坐標系下三維坐標；ΔX、ΔY、ΔZ、εX、εY、εZ、m為7個參數。

通過這樣的過程改進，不但計算結果更為精確，7個參數的物理含義也很明晰。

(3) 轉換步驟

1) 利用GPS C級點計算的1980西安坐標系/1954北京坐標系→CGCS2000坐標系的參數，將參與1980西安坐標系/1954北京坐標系天文大地網聯合平差的地面網點概略改算到2000國家大地坐標，然后根據點名、點位(B，L)，對照CGCS2000系成果查找重合點。以此為基礎，利用新舊成果的正常高信息，檢查正常高是否發生大的變化，以此來確認該標石是否發生變動，進一步甄選重合點。

2) 將重合點坐標換算為大地坐標及空間直角坐標。

3) 使用篩選出的全部重合點求取轉換參數(三維轉換)，再利用該轉換參數回代，求得已知點的坐標，計算已知點的殘差。

4) 分析殘差值大于2～3倍殘差中誤差的點的可靠性，檢查點位和成果的正確性，重新確定重合點。

5) 再重復步驟3)和4)，直到回代殘差到一定范圍內為止，最終確定參與求解參數的已知點。

根據上述步驟，可計算出1980西安坐標系/1954北京坐標系→CGCS2000坐標系的參數(見表1)。

表1 七參數及中誤差統計

2. 柵格法改正模型

(1) 改算步驟

①甄選已知點，剔出與周圍互差較大的異常點；②確定柵格改正量的空間格網大小；③根據已知點分布及空間插值特點，劃定柵格改正量的有效范圍；④計算經度B、緯度L兩個分量的柵格改正量；⑤結果檢驗。

(2) 改算過程

1) 根據已知點改正量，利用TIN計算已知點構成的每一個三角區的變化梯度，得出已知點經度、緯度改正量的差分值，在不影響使用精度的前提下確定格網大小。其中，緯度的殘差梯度最大值0.002 45°、經度的殘差梯度最大值0.003 72°，對應到平面距離上，每1000 m分別對應64.9、42.8 mm。

2) 經反復試算得出，改正量的格網大小為100 m時，在改正量變化最大的區域，由規則格網存儲引起的誤差：在X方向<6.49 mm、在Y方向<4.28 mm。因此，本省改正量的格網大小定為100 m左右(實際執行為3″)。

3)雖然收集了云南省周邊一定緩沖區域的已知點成果，但云南地處邊境，國外部分沒有可用的已知點。并且采用的IDW方法要對已知點的殘差改正量進行空間插值，該方法具有一定外推特性，若外推距離遠，則精度低。結合現有已知點及本省1∶1萬地形圖生產的需要，確定了柵格改正量的有效值范圍。

(3) 柵格改正量的計算

利用布爾莎模型系統轉換后，在已知點上還有殘留誤差，可對這些殘差再次進行改正。利用式(2)計算各柵格點的殘差改正量，再利用模型計算系統改正量，兩者疊加(系統+殘差)形成最后成果。

3. 精度評定

模型坐標轉換的精度是通過求取轉換參數的重合點的殘差來體現的。坐標轉換精度估計依據以下公式計算

1) 殘差V=重合點轉換坐標-重合點已知坐標。

2) 空間坐標X與平面坐標x的殘差中誤差為

(5)

3) 空間坐標Y與平面坐標y的殘差中誤差為

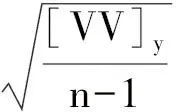
(6)

4) 空間坐標Z與大地高H的殘差中誤差為

(7)

(8)

此外，對轉換成果還采用了外業聯測檢測和與GPSC級點成果進行對比檢驗的方式開展了精度檢核工作。

(1) 七參數模型計算精度評價

此次驗證工作，使用的點共有2443個，其中已知點1222個、檢驗點1221個。為驗證“模型殘差(已知點殘差中誤差)”評定指標的可靠性，將篩選出一半的重合點用作已知點計算模型參數，而另一半重合點用作檢驗點進行改算精度檢驗。七參數模型的誤差見表2。最后，再與全部作為已知點的模型殘差作比較(見表3)。

表2 七參數模型誤差統計

表3 模型殘差與檢驗中誤差的比較 m

從表3可以看出，1222個點與2443個點的模型殘差與1221個點的檢驗中誤差基本相當。再從檢驗中誤差的大小、空間分布(圖略)上看，兩者也基本一致。

依據式(6)—式(8)可計算出，1980西安坐標系到CGCS2000改算模型殘差：RMS dS=0.283 69 m，dS<0.3 m的占73.33%，最小值為0.012 002 m，最大值為0.88 m，在貢山縣境內(麻紀娃Ⅱ)；1954北京坐標系到CGCS2000改算的模型殘差：RMS dS=0.718 46 m，dS<0.5 m的占61.2%，最小值為0.011 4 m，最大值為3.124 m，在貢山縣境內(卡瓦嘿Ⅱ)。轉換模型殘差區間統計見表4。

從表4中可以看出，1980西安坐標系到CGCS2000改算模型殘差和1954北京坐標系到CGCS2000改算的模型殘差差異較大，各點位差值范圍的統計比例差異明顯。1980西安坐標系到CGCS2000改算模型殘差的點位誤差差值范圍集中在[0～0.15]、[0.15～0.3]，占73.33%；而1954北京坐標系到CGCS2000改算模型殘差的點位誤差差值范圍集中在[0.3～0.5]、[0.5～0.883 6]，占63.67%。

表4 轉換模型殘差區間統計

(2) 柵格模型計算精度評價

按照常理，改正量在空間分布上不應有大的突變；另外，按照計算改正量公式(式(2))的特點，在已知點上應有殘差為0的特性。

① 圖面檢驗

對1980西安坐標系到CGSC2000的經度(dL)、緯度(dB)，分別用色彩表示(圖略)，色彩過渡均勻，沒有突變現象。

對1954北京坐標系到CGCS2000的經度(dL)、緯度(dB)，分別用色彩表示(圖略)，除西北角色彩稍有不均勻外，其余色彩過渡均勻，沒有突變現象。

② 已知點殘差檢驗

1980西安坐標系已知點殘差檢驗，對在有效范圍內的2374個已知點，讀取柵格改正量、轉換到CGCS2000后，與國家新成果比較，差異均為0，說明1980西安坐標系柵格改正量正確。

1954北京坐標系已知點殘差檢驗，對在有效范圍內的2369個已知點，讀取柵格改正量、轉換為CGSC2000后，與國家新成果比較，差異均為0，說明1954北京坐標系柵格改正量正確。

對1980西安坐標系轉換為CGCS2000檢驗：柵格法計算2392個已知點的平面位置殘差，結果均為0；對1954北京坐標系轉換為CGCS2000檢驗：計算2369個已知點的平面位置殘差，結果均為0。說明柵格法坐標改正量計算正確。

(3) 其他檢驗

利用國家測繪地理信息局提供的云南省1311個1980西安坐標系、CGCS2000的GPS C級點兩套成果，通過篩選128個重合點，利用布爾莎七參數坐標轉換模型解算CGCS2000成果。經檢驗，模型法轉換平面位置殘差中誤差為0.110 m；柵格法轉換平面位置殘差中誤差為0.287 m。

三、結 論

本文根據云南省基礎測繪成果坐標轉換的工作需求，基于坐標系建立的原理，對其轉換方法進行討論與分析，并對結果進行驗證，結論與建議如下：

1) 利用七參數方法和基于七參數的柵格模型改正方法對云南省的基礎測繪成果數據進行CGCS2000大地坐標改算，從概算精度的評價結果來看，兩種方法是可靠的，均可使用。

2) 從兩種方法的檢驗結果來看，模型法比柵格法的改算點位殘差要小，但這不能說明模型法的結果更好，只能說明模型法與國家測繪地理信息局的轉換法方法更接近。柵格改正法可用于高精度要求的坐標改算。對精度要求不高或需要保持舊成果整體精度的場合，只需利用七參數方法進行改正即可。

3) 在高等級控制點較稀少的地區，可酌情考慮選用三、四等控制點成果作為已知點，以保證圖形結構。

4) 由于空間坐標轉換需要用到大地高，而GPS測量可直接獲取大地高，CGCS2000的新成果就直接提供了大地高。但1954北京坐標系、1980西安坐標系不是真三維空間的坐標，其提供的正常高成果是通過水準、三角高程測量得出的，與坐標成果是相互獨立的，大地高需要間接推算獲取。王文利等的研究結果表明[8]，重合點的大地高誤差對布爾莎參數模型轉換的平面結果影響較小，大地高誤差在10 m以內時，基本不影響轉換的平面結果。而轉換點的大地高誤差對布爾莎七參數模型轉換的平面結果影響非常小。轉換點大地高誤差≤100 m時，可用正常高代替大地高進行轉換，且轉換結果不受影響。因此，在本次研究中，1954北京坐標系、1980西安坐標系的高程異常值可通過《1980西安大地坐標系統成果圖集》獲取，且精度不受影響。

5) DEM、DOM數據由于生產單位提交的原始數據部分缺少坐標信息，沒有頭文件或頭文件格式不對的均轉換失敗，須補充頭文件，手工將頭文件里的坐標值加改正量平移。

6) 靠近中央子午線的圖幅，DLG數據中的部分要素難以獲取改正量，需重新設置帶號進行轉換。

[1] 鐘業勛,童新華,王龍波.從1980西安坐標系到2000國家大地坐標系的坐標變換[J].海洋測繪,2010,30(1):1-3.

[2] 過家春,趙秀俠,吳艷蘭.空間直角坐標與大地坐標轉換的拉格朗日反演方法[J].測繪學報,2014,43(10):998-1004.

[3] 王海棟,柴洪洲,宋國大. 大地坐標系換代對海圖的影響分析[J].測繪通報,2009(1):6-9.

[4] 曾安敏. 基于擬合推估的1980西安坐標系到2000國家坐標系的變換[J].大地測量與地球動力學，2008,28(5):125-128.

[5] 呂志平,魏子卿,李軍,等. 我國CGCS2000高精度坐標轉換格網模型的建立[J]. 測繪學報,2013,42(6):797-791.

[6] 李新,程國棟,盧玲.空間內插方法比較[J].地球科學進展,2000,15(3):260-265.

[7] 李小文,曹春香,常超一.地理學第一定律與時空鄰近度的提出[J].自然雜志,2007(2):69-71.

[8] 王文利,郭春喜,程傳錄.大地高誤差對Bursa七參數平面轉換精度的影響[J].測繪科學,2011,36(5):37-38.

Study on Coordinate System Conversion Methods from BJ54，XA80 to CGCS2000 of Surveying and Mapping Archives in Yunnan Province

ZHOU Junsong，LI Shihua，LI Wenhua，PENG Shuangyun

2016-07-19

國家自然科學基金(41561086)；國家測繪地理信息局地理國情監測示范項目(測國土函〔2014〕35號)

周峻松(1968—)，男，高級工程師，主要從事地圖制圖、遙感與地理信息工程和應用項目管理等工作。E-mail: 78121467@qq.com

李石華。E-mail：lsh8010@163.com

周峻松，李石華，李文華，等.云南省測繪成果向2000國家大地坐標系轉換的方法[J].測繪通報，2016(11)：80-84.

10.13474/j.cnki.11-2246.2016.0371.

P258

B

0494-0911(2016)11-0080-05