基于灰色層次分析法-BP神經網絡的數據鏈系統效能評估*

陳 強,陳長興,陳 婷,程蒙江川

(1 空軍工程大學理學院,西安 710051;2 西安郵電大學,西安 710051)

?

基于灰色層次分析法-BP神經網絡的數據鏈系統效能評估*

陳 強1,陳長興1,陳 婷2,程蒙江川1

(1 空軍工程大學理學院,西安 710051;2 西安郵電大學,西安 710051)

為進一步提高效能評估的可信性及智能化水平,提出了一種基于灰色AHP理論的數據鏈系統BP神經網絡效能評估模型。從數據鏈系統性能結構出發,針對數據鏈信息優勢的特點,建立了數據鏈系統作戰效能評估指標體系。通過專家組依據標準打分的方式,采用AHP確定指標的權重向量,考慮借助灰色理論白化指標,最后與不同灰類分效能值聚合生成綜合效能評價值從而建立了效能輸出模型。構造三層BP神經網絡模型,以專家的知識與經驗作為輸入,以灰色AHP綜合效能評價值作為輸出訓練網絡。最后通過實例驗證,由于該模型運用BP神經網絡非線性擬合的優勢繼承并有效聚合了專家的知識與經驗,結果與專家評定一致,從而論證了模型的有效性及可靠性,為數據鏈系統效能評估提供了智能化的算子,在數據鏈的發展和應用中發揮重要作用。

數據鏈系統;指標體系;灰色系統理論;層次分析法;BP神經網絡

0 引言

數據鏈系統是指一種能夠按照統一的數據格式和約定的通信協議,通過有線或者無線信道(以無線信道為主)對格式化信息進行實時、可靠、安全、保密傳輸的數據通信與處理系統[1]。數據鏈系統的應用,使獨立的作戰單元相互“鉸鏈”、“耦合”,各作戰單元彼此構成一個數據通信網絡,同時還可以對接收到的各種有效信息(本作戰單元的傳感器信息及目標威脅信息以及從其他作戰單元接收的信息)進行(融合)處理,在一定程度上實現大量信息共享、高效實時的戰場指揮、實時精確的武器協同、態勢共享等功能[1-2]。數據鏈系統在現代信息化條件下的戰場上扮演了愈發重要的角色,是現代信息戰爭的“倍增器”,

因此研究數據鏈系統的效能評估將對數據鏈裝備的發展和應用起到極大的推進作用。

灰色系統理論實現了不確定性系統在信息貧乏條件下由“灰”生成“白”,從而很好的提高系統指標量化的準確性和可信度。而層次分析法通過定量分析與定性分析相結合的方式解決了層級之間、指標之間權重問題。二者的結合為效能評估提供了新思路,同時克服了專家主觀性及最大限度的利用專家的評判結果,使評估結果更為準確和可信。

現有文獻中,大多集中在利用評估理論和方法支撐指標到效能的數據對應關系,造成評估過程繁瑣結果缺乏可信性。在文獻[3]倚靠BP(back propagation)神經網絡的非線性擬合能力很好的解決了評估指標到效能值的映射問題,但網絡訓練以“灰色”貧樣本的專家打分值作為輸出值其結果顯然缺乏可信度和準確性。文獻[4]從系統內部權重因子耦合出發,引用經典理論分層分析法(analytic hierarchy process,AHP)來構造BP神經網絡訓練樣本,有一定的借鑒意義。文獻[5]吸收灰色系統理論指標評判“漂白”的優點,評價值具有一定的可信性和準確性。文獻[6]聚合灰色理論的“漂白”功效及AHP的權重耦合特性,具有理論借鑒意義,但文中過程較為復雜,亟待在繼承專家經驗和知識的基礎上簡化指標到效能的映射過程。

文中在灰色層析分析法的基礎上利用BP神經網絡的非線性擬合能力,以白化的專家評判值作為輸入,以灰色AHP評估結果作為輸出,從而合理的繼承了專家的知識與經驗,為數據鏈系統評估提供了算子化的思路。

1 基本思路

1)建立系統指標體系H遞階層次結構;

2)利用層次分析法確定指標權重ω及ωi,再運用灰色系統理論白化指標向量進而求解最大限度地包含專家水平與經驗的評判值;

3)構建BP神經網絡評估模型結構;

4)選取經過白化的專家評分輸入樣本及灰色AHP評估結果輸出樣本,訓練網絡直至滿足精度。

具體流程如圖1所示。

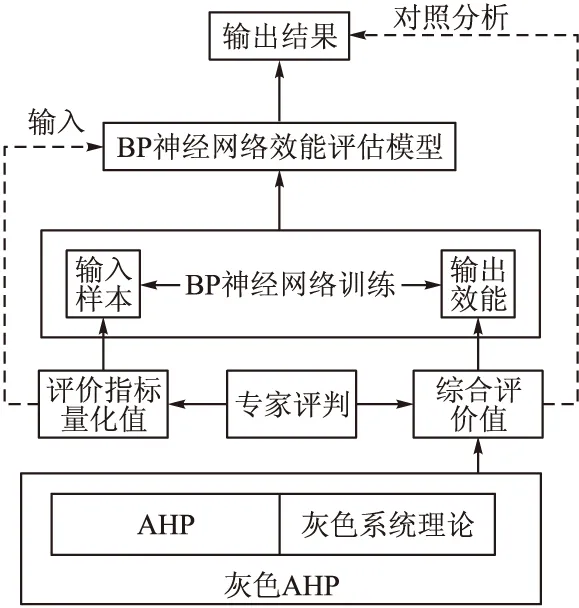
圖1 灰色AHP-BP神經網絡評估模型

2 數據鏈系統作戰效能評估指標體系

數據鏈系統作戰效能評估指標體系的構建必須遵循系統性原則、可比性原則、定性和定量相結合原則、獨立性原則、層次性原則和客觀性原則,同時又要考慮到影響數據鏈系統作戰能力影響因素比較多的特點[5]。在分析數據鏈系統功能、結構和特點的基礎上,根據數據鏈信息傳遞的實時性、信息處理的可靠性、安全保密及交互戰術信息的要求,文中從信息處理能力、信息傳輸能力、網絡管理能力、信息安全防護能力、可用性及可信性六個方面來分析數據鏈系統的效能,建立了如圖2所示的數據鏈系統作戰效能評估指標體系[6]。

圖2 數據鏈系統效能評估指標體系

3 灰色AHP模型的建立

3.1 評價指標權重的確定

依據層次分析法的基本原理,在已構建的指標體系的基礎上,選取相關領域專家參照1-9標度針對各層元素關于準則層的重要性進行兩兩比較從而形成判斷矩陣。這里采用和積法來計算生成的判斷矩陣A的最大特征值λmax及特征向量ωi,即為指標層評價指標hij的相對權重并同樣記為ωi,其中一級指標相對權重記為W,具體運算步驟如下:

1)將矩陣A中元素按列分別歸一化,即求得:

(1)

2)將歸一化矩陣按行分別相加,即:

(2)

3)將wij按列歸一化即得權重向量,即:

(3)

4)計算矩陣A的最大特征根,記為:

(4)

表1 系統效能H1的判斷矩陣及權重向量ω1

3.2 構造評價指標樣本矩陣

將指標評分等級劃分為4類,分別對應優、良、中、差4個評分標準,對應分值分別為4、3、2、1分,考慮到評判過程中出現的模糊類別,細化增加了3個中間等級標準,賦值分別為3.5、2.5、1.5分。

依據以上評分標準,遴選了n位專家分別對某型數據鏈系統各評價指標評判打分,制作了如表1所示的按遞階層次結構給出的評分表,依據指標優劣分別在發放的評分表中給出對應分值。

綜合n位專家的評分結果得到某型數據鏈系統的評估樣本矩陣:

其中:i=4,j=25,hijl表示第l位專家對指標hij的評分值。

3.3 確定評估灰類

評估灰類涉及的3個重要屬性分別是評估灰類的等級數、灰類的灰數及灰類的白化權函數[6],三者的確定是關鍵。根據指標評分等級標準設定4個評估灰類,即e=1,2,3,4,分別對應優、良、中、差4個等級,相應的白化權函數依次為:

1)第一灰類“優”(e=1),灰數設定為?∈[4,+∞),其對應的白化權函數為f1,如圖3所示;

2)第二灰類“良”(e=2),灰數設定為?∈[0,3,6),其對應的白化權函數為f2,如圖4所示;

3)第三灰類“中”(e=3),灰數設定為?∈[0,2,4),其對應的白化權函數為f3,如圖5所示;

4)第四灰類“差”(e=4),灰數設定為?∈[4,∞),其對應的白化權函數為f4,如圖6所示。

圖3 第一灰類

圖4 第二灰類

圖5 第三灰類

圖6 第四灰類

3.4 計算灰色評價權重及構造灰色評價矩陣

對于數據鏈系統指標Hi對應的二級指標層評價指標hij,將n位專家評判打分值依次代入e(e=1,2,3,4)灰類相應的白化權函數得e灰類灰色評估系數,記為xije,總評估系數記為xij,具體數學表達式為:

則e灰類的灰色評價權系數為:

rije=Qije/Qij

由以上關系,容易得出數據鏈系統底層指標hij對于4個等級灰類的灰色評價矩陣Ri為:

3.5 計算數據鏈系統作戰效能的綜合評估值

1)將灰色評估權矩陣Ri與數據鏈系統評價指標Hi對應二級指標hij的相對權重結合,得到綜合效能評估值,記為Di,即:

2)由評價指標Hi的綜合評估效能值Di聚合得到系統一級指標H總的灰色評估矩陣R。

據此可以求出數據鏈系統總的灰色評估結果D為:

D=ωT·R=[d1,d2,…,d5]

3)將四灰類依據等級標準賦予不同的分效能值,其組成的分效能向量設定為C=[9,7,5,3],以此對總的灰色評估矩陣進行歸一化處理,得到數據鏈系統作戰效能評估值E為:

E=D·CT=[d1,d2,…,d5]·[9,7,5,3]T

數據鏈系統綜合評估效能值即為所求。

依據上述理論及計算方法,考慮各指標等級劃分及對應量化賦值不同,可將綜合評價值按標準劃分為4個檔次。當專家對指標Hij一致評定為4分時,得到的綜合評價值為E=8.200;評定一致為3.5分時E=7.638 3;評定一致為3分時E=7.222;評定一致為2.5分時E=6.886 8;評定一致為2分時E=6.538 3;評定一致為1分時E=4.840。從而根據綜合評價值區間等級分類如表2所示。

表2 5個分類等級評估值區間

4 灰色AHP-BP神經網絡評估模型的實現

BP神經網絡的非線性逼近能力對于解決數據鏈系統效能評估問題提供了一個新的思路[4,6],為系統效能評估設計了算子化的模型。文中采用典型的三層BP神經網絡模型,即包含輸入層、隱含層及輸出層[3]。具體結構如圖7所示。其中輸入層神經元節

圖7 BP神經網絡結構示意圖

其中隱含層激活函數f設置為S型函數:

4.1 選取訓練樣本

訓練樣本的選取對網絡的性能至關重要,關系著效能評估的可信性和準確性。文中從這兩點出發,選取10位專家分別依次對各指標評判打分,抽取灰色層次分析法白化指標作為輸入值,灰色層次分析法評估值作為輸出值作為原始訓練樣本。具體數據如表3所示(由于篇幅限制僅截取部分樣本值)。

表3 專家評判打分及綜合評估值

4.2 網絡訓練及仿真學習

將上述樣本值用于對網絡進行訓練,直到滿足設定的精度要求才結束。部分網絡性能參數設置如下:

net.trainParam.epochs=7 000;

%設置網絡訓練次數

net.trainParam.show=100;

%設置顯示間隔的訓練次數

net.trainParam.mc=0.09;

%設置附加動量常數

net.trainParam.goal=1e-50;

%設置允許誤差范圍

net.trainParam.lr=0.15;

%設置網絡學習速率

網絡訓練的誤差曲線如圖8所示,當學習到100次時訓練結束,表明網絡已經滿足了誤差精度要求,此時BP神經網絡已建立了從專家評價到系統效能等級評價的映射。

為了驗證BP神經網絡評估模型的準確性及實用性,以某型數據鏈系統為例,以專家依據等級評價作為輸入送到訓練好的網絡中,輸出結果與專家總體評價進行對比分析。結果如表4所示。顯然從表4中容易得到神經網絡輸出值與專家總體評價吻合,同時結合灰色層次分析法結果進行對照分析結論一致,從上述結果可以得出BP神經網絡數據鏈系統評估模型結構合理,結果比較理想,可以用于數據鏈系統的效能評估,進一步為數據鏈系統的應用提供了理論參考及智能化的評估,具有一定的應用價值,也為評估方法和理論開辟了一個新的方向和創新點。

表4 仿真結果對照分析表

圖8 誤差曲線圖

5 結束語

針對數據鏈性能特點及信息優勢建立數據鏈系統效能評估指標體系,并采用基于灰色AHP-BP神經網絡的評估方法。首先構建灰色AHP模型建立從專家評判值到效能評價值的輸出模型,以此采集網絡輸入輸出樣本,接下來采用BP神經網絡非線性擬合能力把體現專家知識與經驗的等級評分值映射到系統效能,最后通過實例分析結果理想可靠,為評估理論指明了一個新的方向。文中也只是在貧樣本環境下訓練網絡,下一步將結合其他優化算法進行探索研究,考慮擬和能力更強的優化算法在大樣本訓練條件下評估的準確性。

[1] 潘寒盡, 張德和, 邱學軍. 基于模糊灰色理論的數據鏈系統作戰效能評估 [J]. 現代防御技術, 2001, 39(4): 60-64.

[2] 呂娜. 數據鏈理論與系統 [M]. 電子工業出版社, 2011: 36-40.

[3] 周燕, 陳烺中, 李為民. 基于BP神經網絡的彈炮結合系統作戰效能評估 [J]. 系統工程與電子技術, 2005, 27(1): 84-86.

[4] 陳佳昀, 武斌, 唐唐. AHP和BP神經網絡在通信效能評估中的應用 [J]. 現代電子技術, 2009, 25(7): 65-67.

[5] 潘寒盡, 張德和, 邱學軍. 基于模糊灰色理論的數據鏈系統作戰效能評估 [J]. 現代防御技術, 2011, 39(4): 60-64.

[6] 陳士濤, 張志峰, 歸建洲. 基于灰色理論的電子維修車保障效能綜合評估 [J]. 系統工程與電子技術, 2009, 31(4): 994-996.

[7] 李志猛, 徐培德, 冉承新. 武器系統效能評估理論及應用 [M]. 北京: 國防工業出版社, 2013: 50-56.

[8] 王銳, 張安, 史兆偉. 基于冪指數法和AHP的先進戰斗機效能評估 [J]. 火力與指揮控制, 2008, 33(11): 73-76.

[9] 孫繼銀, 付光遠. 戰術數據鏈技術與系統 [M]. 北京: 國防工業出版社, 2009: 80-95.

[10] 韓曉明, 張金哲, 張君. 基于指數法的航空裝備對比優勢評估模型 [J]. 系統工程與電子技術, 2009, 31(6): 1409-1414.

[11] 軒永波, 黃長強, 王勇. 基于灰色層次分析法的空間武器作戰效能評估 [J]. 空軍工程大學學報, 2011, 12(2): 32-37.

[12] LEE B R, JUNG E K, CHOE S. Link-16 simulator design over jamming environments and Link-16 performance analysis with or without time synchronization [J]. Telecom Reviewm, 2013, 23(2): 261-275.

Efficiency Evaluation of Data Link System Based on Gray AHP-BP Neural Network

CHEN Qiang1,CHEN Changxing1,CHEN Ting2,CHENG Mengjiangchuan1

(1 Science College, Air Force Engineering University, Xi’an 710051, China;2 Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

In order to improve the level of credibility and intelligence of efficiency evaluation, a BP neural network effectiveness evaluation frame of data link system on the basis of gray AHP theory was proposed. Considering performance and structure of data link system, according to the characteristics of advantage of data link information, the operational effectiveness assessment index system of data link was established. Through expert marking by standard, using AHP to determine the weight vectors of index, considering to use the albino indicators index of gray theory aggregate with different gray class efficiency value to generate comprehensive efficiency evaluation so that the output efficiency model was established. A three-layer BP neural network model was structured with the expert’s knowledge and experience as input, and the grey AHP comprehensive efficiency evaluation value as the output of the training network. Finally, the experiment validated that the result was consistent with the expert evaluation. Since the model uses the advantage of nonlinear fitting inheritance of BP neural network and aggregates the expert’s knowledge and experience effectively, therefore, it demonstrates validity and reliability of the model and provides intelligent operator for the data link system effectiveness evaluation. The model plays an important role in development and application of the data link.

data link system; index system; gray system model; analytic hierarchy process; BP neural network

2015-07-10

陜西省自然科學基礎研究項目(2014JM8344)資助

陳強(1989-),男,江西南昌人,碩士研究生,研究方向:數據鏈系統效能評估及影響分析。

TN919

A