抗野值卡爾曼濾波在火箭彈落點估計中的應用*
閆小龍,陳國光,楊 東
(1 中北大學,太原 030051;2 豫西工業集團有限公司,河南南陽 473000)
?
抗野值卡爾曼濾波在火箭彈落點估計中的應用*
閆小龍1,陳國光1,楊 東2
(1 中北大學,太原 030051;2 豫西工業集團有限公司,河南南陽 473000)
為了實現火箭彈精確打擊,根據飛行彈道參數對彈道進行修正。應用文中提出的雙氣動參數辨識算法,去除出現在信號初始階段的野值,降低對后續卡爾曼濾波的影響。隨后利用基于新息判斷野值的卡爾曼濾波器,結合質點彈道模型,建立了卡爾曼濾波彈道模型,對一段飛行參數進行野值的去除與濾波,并對火箭彈落點進行外推。結果表明,該方法可以將量測數據中的野值有效去除。落點估計可知,外推時間的推后可以增加預估的精度。
火箭彈彈道修正;卡爾曼濾波;雙氣動參數辨識;野值;落點估計
0 引言
隨著對火箭彈的射擊精度要求的不斷提高,修正火箭彈逐步被廣泛的應用。其工作原理是根據火箭彈的飛行觀測數據(如雷達數據、GPS數據等)對火箭彈飛行狀態進行最優估計并預測落點,并將預測落點與擬擊中目標進行比較,計算出偏差,根據偏差的大小對火箭彈進行修正。
文中針對使用三坐標雷達對火箭彈飛行軌跡觀測,在觀測過程中由于雷達探測有較大的誤差,就使得在對火箭彈進行落點估計時使用的數據有較大的影響。這就要求對彈道數據進行濾波,濾除雷達信號中的隨機噪聲。但是在雷達實際探測中不但會有隨機噪聲,而且還會有較少但是與實際數值偏差較大的噪聲,這些偏差較大的噪聲稱為“野值”,在濾波過程中這些野值會對濾波算法有較大的影響,嚴重影響處理結果精度。在此前提條件下文中提出一種帶有野值剔除的卡爾曼濾波算法,提高了對火箭彈落點估計的準確度[1]。
1 火箭彈外彈道濾波、外推模型
在得到雷達量測數據后,要根據彈道模型對實測彈道進行濾波處理,并外推落點[2],之后及時的反饋偏差數據,隨之火箭彈的執行機構進行彈道修正。由于修正火箭彈需要及時的解算進行落點估計,所以在同時要求解算速度與解算精度的前提下,選擇計算速度較快的質點彈道模型。
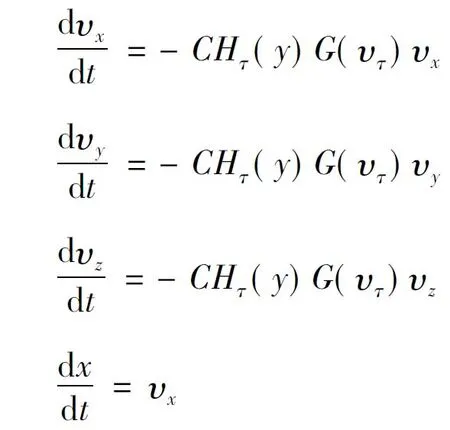
(1)
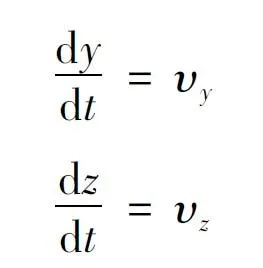
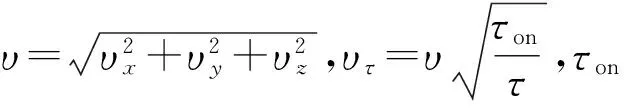
取x1、x2、x3、x4、x5、x6作為卡爾曼濾波的狀態變量,即(x1,x2,x3,x4,x5,x6)T=(vx,vy,vz,x,y,z)T。則有系統狀態方程:
(2)
式中W(k)是均值為零的隨機噪聲。
2 濾波量測方程
三坐標雷達的測量值,即斜距r,方位角β和高低角ε。可得雷達測量值與地面坐標系的關系:
(3)
式中,(x0,y0,z0)為雷達天線中心在地面坐標系中的坐標。
坐標雷達的測量陣列為Z=[r,β,ε]。Vk為雷達測量噪聲,假定為零均值的高斯白噪聲,則離散形式的量測噪聲方差矩陣為:
(4)
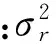
在火箭彈發射過程中,雷達坐標系并不正好處于炮位坐標系,則需要坐標系之間的轉換,轉換關系為:
式中:εx、εy、εz為三維空間直角坐標變換的3個旋轉角,R1(εx)、R2(εy)、R3(εz)分別為與它相對應的旋轉矩陣。
則可得量測方程為:
(6)
3 卡爾曼濾波
卡爾曼濾波方程組分為兩大部分,第一部分為卡爾曼濾波方程,這一部分負責向前推算軌跡狀態;第二部分為卡爾曼濾波器的增益矩陣遞推算式,這一部分用于反饋先驗估計,并對預測進行修正。離散系統的卡爾曼最優估計基本公式為[3]:
最優預測估計方程:
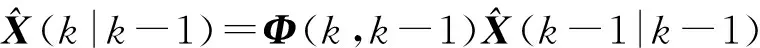
(7)
最優濾波估計方程:
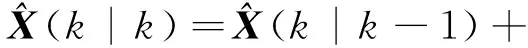

(8)
最優濾波增益矩陣方程:
K(k)=P(k|k-1)HT(k)·
[H(k)P(k|k-1)HT(k)+Rk]-1
(9)
最優預測估計誤差方差陣方程:
P(k|k-1)=Φ[k,k-1]P(k-1|k-1)·
ΦT(k,k-1)+Γ(k|k-1)Qk-1ΓT(k|k-1)
(10)
最優濾波估計誤差方差陣方程:
P(k|k)=K(k)RkKT(k)+
[I-K(k)H(k)]P(k|k-1)[I-K(k)H(k)]T
(11)
t0時刻的狀態向量X(0)的統計特性E{X(0)}及P(0)都已知道,那么,為了得到無偏估計,應取值:
4 野值的判別與處理
由于在實際情況中,量測信號要經過傳輸系統、數據采集轉換系統等環節,才能把數字形式的目標信號送卡爾曼濾波,這樣不但會帶有大量的隨機噪聲,而且有可能受到外界無規律的干擾而產生一些與真實數據相差較大的野值,這些野值的存在使得在進行卡爾曼濾波時對濾波結果有較大的影響[4]。
令:
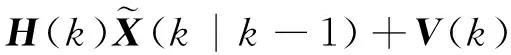
(12)
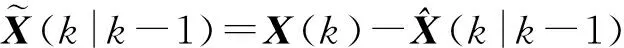
H(k)P(k|k-1)HT(k)+R(k)
(13)
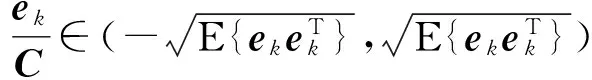
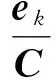
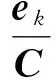
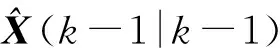

(14)
根據式(14)對此n點進行拋物線擬合,并計算殘差δ1~δn。
當δi>C時,認為該點為野值點,并去除;
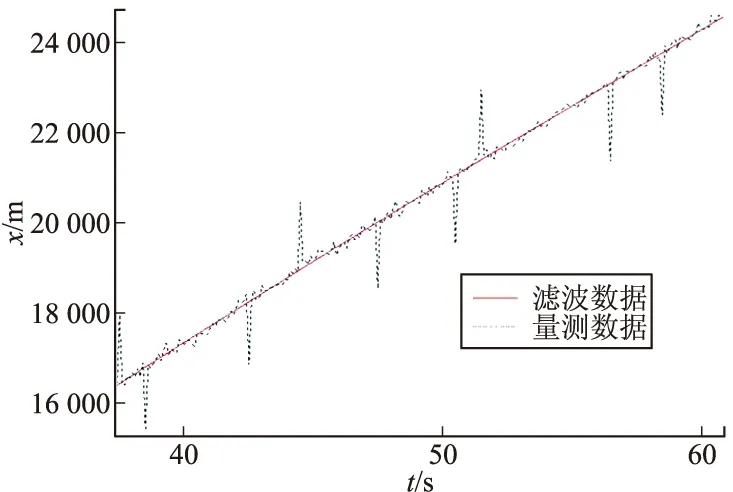
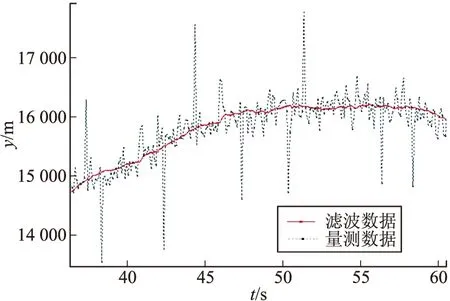
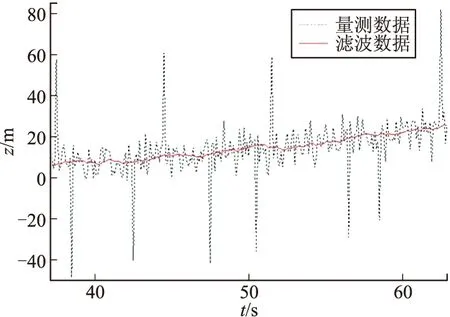
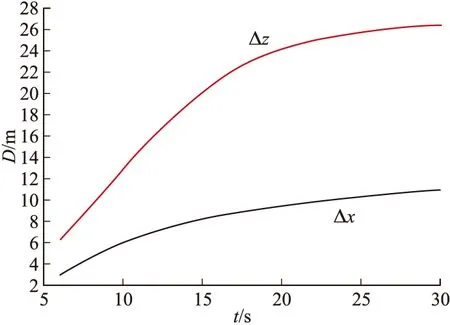
當δi 為了檢驗該濾波器的實際濾波效果,需要對其進行數值仿真計算。文中以某型火箭彈為例進行仿真,采用5D彈道模型計算生成彈道數據,然后加入均值為零的高斯白噪聲引入雷達噪聲,加入不定周期的較大誤差作為引入的雷達測量野值,形成三坐標雷達量測數據[5]。用帶野值處理卡爾曼濾波器對雷達測得的數據進行野值的判別、處理、濾波,并用質點外彈道方程外推彈道,預估落點(x,z),模擬彈丸發射2.5 s后雷達開始跟蹤量測目標,采樣間隔為0.1 s。在模擬雷達量測數據至40 s左右,開始對彈道數據進行濾波處理,持續監控20 s左右至60 s時停止濾波處理。圖1~圖3為野值去除以及濾波處理結果。 圖4為帶去野值功能的卡爾曼濾波后原數據的差,結果表明濾波后的差值收斂很快,經過20 s后趨于穩定。圖5為不帶去野值功能的卡爾曼濾波后原數據的差,結果表明濾波后的差值在經過40 s后才趨于穩定,且差值較有去野值功能的卡爾曼濾波要大很多。當野值去除以及濾波工作結束后取60 s時的濾波數據結果,并輸入質點彈道方程對火箭彈落點(x,z)進行估計。并最終與生成的彈道進行對比,得出落點估計的差值。圖6為x方向上預估落點與原彈道差值,圖7為z方向上預估落點與原彈道差值。 圖1 x方向數據處理 圖2 y方向數據處理 圖3 z方向上的數據處理 圖4 去野值濾波坐標軸方向上的濾波后原數據差 圖8為外推彈道落點坐標誤差與外推開始距擊中目標時長的關系,由圖可以看出隨著外推時間的不斷提前,其外推的精準度逐步降低。但是在提前到一定的時間后,精度降低的速度逐步放緩而趨于穩定。因此合適的選取外推開始時間可以有效的增加落點預測的精度,但是一再的推遲外推時間,降低了落點估計的意義。 圖5 不去野值濾波坐標軸方向上的濾波后原數據差 圖6 x軸外推落點與原彈道差 圖7 z軸外推落點與原彈道差 圖8 外推開始時刻距落地時刻的時長與落點估計精度的關系 文中針對三坐標雷達量測的火箭彈彈道數據,通過可以去除量測數據中野值的卡爾曼濾波器濾除雷達測量信號中的隨機噪聲,根據濾波結束時的彈道數據輸入外推質點彈道方程,得到估計落點,為火箭彈的修正提供了有效數據。用生成彈道數據進行數據仿真結果表明,在有野值存在且雷達的隨機噪聲幅值很大的情況下,經過該濾波器濾波后可以獲得較為接近真實值的彈道數據。在外推過程中,隨著外推時間的不斷推后,外推的精度會不斷的提高。 [1] 俞濟祥. 卡爾曼濾波及其在慣性導航中的應用 [M]. 北京: 航空專業教材編審組, 1984: 101-102. [2] 王志賢. 最優狀態估計與系統辨識 [M]. 西安: 西北工業大學出版社, 2004: 76. [3] 高寧, 周躍慶, 楊曄, 等. 抗野值自適應卡爾曼濾波方法的研究 [J]. 中國慣性技術學報, 2003, 11(3): 25-28. [4] 張遠, 陳勇, 吳昊. 彈道導彈落點預報方法研究 [J]. 導彈與航天運載技術, 2014(3): 5-10. [5] 李廣軍, 李忠, 崔繼仁. 新型抗野值的Kalman濾波器研究 [J]. 計算機應用與軟件, 2013, 30(1): 136-138. Application of Kalman Filter Restraining Outliers in Estimation of Rockets Impact Point YAN Xiaolong1,CHEN Guoguang1,YANG Dong2 (1 North University of China, Taiyuan 030051, China; 2 Yuxi Industries Group Co. Ltd, Henan Nanyang 473000, China) Precise rocket strike, requires trajectory correction according to trajectory parameters. In this paper, double aerodynamic parameter identification algorithm was used to remove appears in initial phase of signal outliers, reduce impact on subsequent Kalman filter. Intermediate outlier measurement information was used to judge based on prediction error of the Kalman filter combined with particle trajectory model for construction of the Kalman filter trajectory model. The Kalman filter trajectory model was used to remove and filter outliers of a section of flight parameters, and extrapolate the rockets impact point. The simulation results show that, the filter can remove and filter the outliers in radar measurement data effectively. We can know that prediction accuracy can increase by postponing extrapolation. rocket trajectory correction; Kalman filter; double aerodynamic parameter identification; outliers; impact point estimation 2015-05-13 閆小龍(1988-),男,山西太原人,碩士研究生,研究方向:智能彈藥。 TJ765 A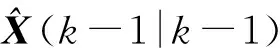
5 計算仿真
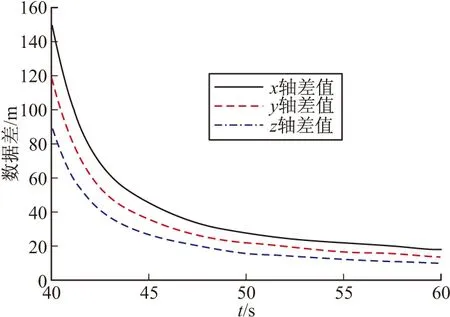
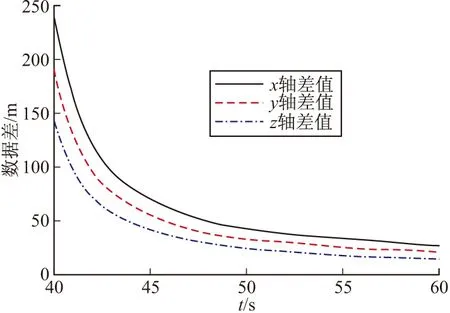
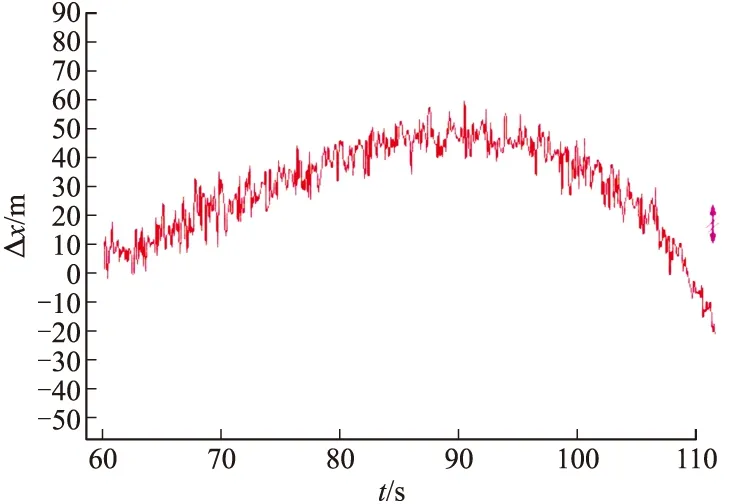
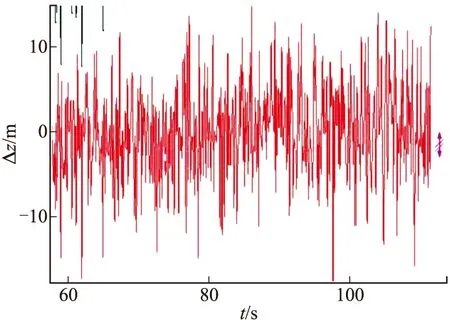
6 總結

