單渦旋場(chǎng)激光傳輸特性研究

許凌飛,畢 鵬,周志超,任天榮

(上海機(jī)電工程研究所,上海201109)

?

單渦旋場(chǎng)激光傳輸特性研究

許凌飛,畢 鵬,周志超,任天榮

(上海機(jī)電工程研究所,上海201109)

對(duì)單渦旋場(chǎng)激光傳輸特性進(jìn)行了研究。用積分方程形式將整個(gè)流場(chǎng)分解成體元，每個(gè)體元中的折射率分布不均勻，用麥克斯韋積分方程替代微分方程求解整個(gè)流場(chǎng)的光場(chǎng)分布，給出了氣動(dòng)渦流折射率場(chǎng)的計(jì)算模型。當(dāng)流場(chǎng)只存在一個(gè)理想渦流且渦流的折射率場(chǎng)有近似的解析形式時(shí)，基于非均勻介質(zhì)散射理論，用Rytov散射近似，由積分方程計(jì)算觀測(cè)平面上光場(chǎng)所受的流場(chǎng)擾動(dòng)。討論了不同激光傳輸距離下流場(chǎng)擾動(dòng)時(shí)的光場(chǎng)空間強(qiáng)度分布。結(jié)果發(fā)現(xiàn)：隨著激光傳輸距離的增加，光強(qiáng)急劇下降，中心位置光強(qiáng)與無(wú)流場(chǎng)擾動(dòng)時(shí)自由空間高斯光束傳輸中心位置光強(qiáng)相近，但在兩側(cè)會(huì)形成一個(gè)暗環(huán)，使激光光場(chǎng)的空間強(qiáng)度分布發(fā)生改變，導(dǎo)致激光脈沖光束出現(xiàn)形變。研究說(shuō)明了用積分方程描述氣動(dòng)光學(xué)效應(yīng)的可行性，為精確計(jì)算復(fù)雜渦結(jié)構(gòu)流場(chǎng)提供了一種新思路。

激光傳輸； 麥克斯韋積分方程； 氣動(dòng)光學(xué)效應(yīng)； 高斯渦旋； 折射率； 空間強(qiáng)度； 流場(chǎng)擾動(dòng)； 傳輸距離

0 引言

飛行器在大氣層中高速飛行時(shí)，其外結(jié)構(gòu)的氣動(dòng)外形與空氣發(fā)生強(qiáng)烈的相互作用，尤其是頭部、舵面和翼周?chē)臍怏w流場(chǎng)密度分布會(huì)發(fā)生很大變化，而氣體的光學(xué)折射性與氣體流場(chǎng)密度密切相關(guān)，因此超聲速飛行常伴有明顯的氣動(dòng)光學(xué)現(xiàn)象[1]。氣動(dòng)光學(xué)主要研究光束與其傳輸路徑上氣體流體介質(zhì)的相互作用而導(dǎo)致光波的速度、方向，以及相位的變化[2-3]。對(duì)理想氣體，湍流和密度的變化是光波的上述參量發(fā)生改變的主要原因，具體可描述為：當(dāng)一束準(zhǔn)直光束穿過(guò)湍流場(chǎng)時(shí)，因折射率的變化而導(dǎo)致其平面波前發(fā)生時(shí)域中的畸變[4]。傳統(tǒng)氣動(dòng)光學(xué)處理時(shí)，在一定的微小領(lǐng)域內(nèi)將折射率視作為均勻的，對(duì)每個(gè)微元應(yīng)用麥克斯韋方程組，獲得光場(chǎng)的空間分布[5]。因在氣動(dòng)效應(yīng)較大的區(qū)域內(nèi)，折射率的不均勻性在空間尺度上變得更小，故在數(shù)值解算時(shí)尺度的選取變得尤為苛刻，可能會(huì)導(dǎo)致對(duì)某些流場(chǎng)的計(jì)算誤差增大。

1952年，LIEPMANN就指出了氣動(dòng)光學(xué)傳輸效應(yīng)的研究應(yīng)是畸變波前與湍流渦動(dòng)力學(xué)特性間的關(guān)系。因此，可壓縮渦問(wèn)題的求解為單渦的氣動(dòng)光學(xué)理論研究提供了基礎(chǔ)。基于一種二維軸對(duì)稱(chēng)的弱可壓縮渦模型，馬小亮等采用幾何光學(xué)方法，研究了單個(gè)渦和光波陣面的相互干擾[6]。單渦模型的研究可向更復(fù)雜的湍流場(chǎng)進(jìn)行推廣。TROLINGER提出了一種基于湍流渦球模型的隨機(jī)屏方法，在流場(chǎng)中隨機(jī)布置不同尺度和密度的渦球模擬瞬態(tài)渦結(jié)構(gòu)引起的密度不均勻分布[7]。在此基礎(chǔ)上，史可天等根據(jù)渦球所在位置的密度脈動(dòng)統(tǒng)計(jì)特性確定渦球與周?chē)黧w的密度差異以及渦球直徑，提高了原有計(jì)算方法的精度，但采用的仍是幾何光學(xué)的方法[8]。房建成等基于小波的分辨特性對(duì)流場(chǎng)的渦結(jié)構(gòu)進(jìn)行識(shí)別，分別采用光線(xiàn)追跡法和統(tǒng)計(jì)光學(xué)法建立大尺度和小尺度渦結(jié)構(gòu)的傳輸模型[9]。綜上，目前的氣動(dòng)光學(xué)研究領(lǐng)域中，主要采取的方式是依靠數(shù)值計(jì)算光場(chǎng)的光程差對(duì)氣動(dòng)光學(xué)效應(yīng)進(jìn)行分析和驗(yàn)證，其要點(diǎn)是基于對(duì)流場(chǎng)離散化后，認(rèn)為離散后的網(wǎng)格尺度遠(yuǎn)大于波長(zhǎng)尺度量級(jí)，從而對(duì)每個(gè)網(wǎng)格內(nèi)的流場(chǎng)來(lái)說(shuō)，其實(shí)質(zhì)是一個(gè)均勻的流場(chǎng)，無(wú)需考慮光場(chǎng)的波前散射效應(yīng)。隨著流場(chǎng)計(jì)算的精細(xì)化，網(wǎng)格可被分割地越來(lái)越密，甚至逼近于一個(gè)波長(zhǎng)尺度，另外激光的相干度很高，波前受到的不均勻特性影響更明顯。在此情況下，現(xiàn)有的氣動(dòng)光學(xué)模型很難準(zhǔn)確描述。本文對(duì)單渦旋場(chǎng)激光傳輸特性進(jìn)行了研究，利用積分方程形式，將整個(gè)流場(chǎng)分解成多個(gè)體元，每個(gè)體元中的折射率分布不均勻，用麥克斯韋積分方程替代微分方程以求解整個(gè)流場(chǎng)的光場(chǎng)分布。

1 激光非均勻介質(zhì)散射理論

1.1 氣動(dòng)渦流折射率

旋渦是一群繞公共中心旋轉(zhuǎn)的流體微團(tuán)，它是氣流運(yùn)動(dòng)的基本元素，常見(jiàn)于飛行器繞流及大氣湍流。當(dāng)流動(dòng)馬赫數(shù)(當(dāng)?shù)亓鲃?dòng)速度與聲速之比)大于0.3時(shí)，須考慮氣體的可壓縮性。在可壓縮流動(dòng)中，氣體的熱力學(xué)參數(shù)(如壓力、溫度和密度)隨時(shí)間和空間會(huì)發(fā)生變化。根據(jù)Gladstone-Dale定律，氣體折射率是密度的函數(shù)。計(jì)算可壓縮流動(dòng)中密度場(chǎng)，可得氣體的折射率場(chǎng)，有

n=1+KGDρ.

(1)

式中：n為折射率；KGD為氣體常數(shù)；ρ為氣體密度。

假設(shè)一沿軸向拉伸的軸對(duì)稱(chēng)可壓縮旋渦(即有限長(zhǎng)圓柱)，長(zhǎng)度為L(zhǎng)，半徑為r，由于速度旋度和壓縮性影響，其橫截面密度沿徑向存在梯度。根據(jù)可壓縮旋渦的理論研究，考慮單個(gè)渦場(chǎng)，即散射體是由一個(gè)軸向拉伸柱狀旋渦組成，沿軸向折射率假設(shè)不變，渦旋場(chǎng)橫截面折射率呈現(xiàn)中間低兩邊高的高斯分布趨勢(shì)，兩邊的折射率趨近于來(lái)流折射率，其密度沿徑向可近似視作高斯分布[10]。則有

n=1-αexp(-s2/W2).

(2)

式中：α為折射率系數(shù)；s為在某流場(chǎng)平面上的半徑；W為渦旋場(chǎng)內(nèi)核半徑。由式(2)，可得

n1=n-1=αexp-s2/W2.

1.2 非均勻介質(zhì)散射理論

當(dāng)光場(chǎng)經(jīng)過(guò)上述非均勻的折射率場(chǎng)時(shí)，會(huì)產(chǎn)生散射，對(duì)光場(chǎng)的空間分布不再滿(mǎn)足霍姆海茲波動(dòng)方程[11]。非均勻場(chǎng)中，光場(chǎng)波動(dòng)方程可表示為

2U+k2(n(x,y,z))2U=0.

(3)

式中：U為光場(chǎng)復(fù)振幅；k為波數(shù)，且k=2π/λ；n為折射率。此處：λ為波長(zhǎng)。

變換式(3)，可得

2U+k2(n0)2U=

k2(n0)2-(n(x,y,z))2U.

(4)

式中：n0為自由空間中的折射率，取n0=1。

考慮整個(gè)折射率場(chǎng)分布處處不均勻，計(jì)算式(3)時(shí)采用積分方程，并用玻恩一階散射近似計(jì)算。玻恩一階散射近似中，認(rèn)為在遠(yuǎn)場(chǎng)的散射場(chǎng)可近似等于入射場(chǎng)U(i)與一階散射微擾U(s)的相干疊加，即

U(r,L)=U(i)(r,L)+U(s)(r,L).

(5)

將式(5)代入式(4)，對(duì)入射場(chǎng)，復(fù)振幅滿(mǎn)足全空間的霍姆海茲方程，且散射場(chǎng)場(chǎng)強(qiáng)遠(yuǎn)小于入射場(chǎng)，則有

[2+k2(n0)2]U(s)=k2[(n0)2-

(n(x,y,z))2]U(i).

(6)

因折射率場(chǎng)變換非常小，故式(4)中的折射率場(chǎng)可近似寫(xiě)成

(n0)2-(n(x,y,z))2≈

2n0[n0-n(x,y,z)].

(7)

將式(6)轉(zhuǎn)換成積分形式，構(gòu)造格林函數(shù)，則

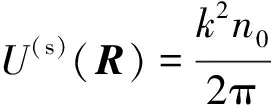
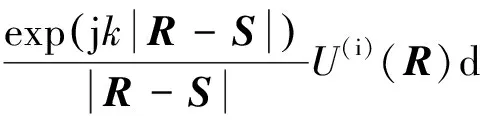
(8)

式中：R=[r z′]=[x′ y′ z′]；S=[s z]=[x y z]。

當(dāng)光場(chǎng)入射至散射體時(shí)，發(fā)生散射如圖1所示。圖中：光場(chǎng)進(jìn)入一個(gè)非均勻介質(zhì)的散射體時(shí)，散射體上一點(diǎn)經(jīng)散射后衍射至觀察平面上一點(diǎn)。

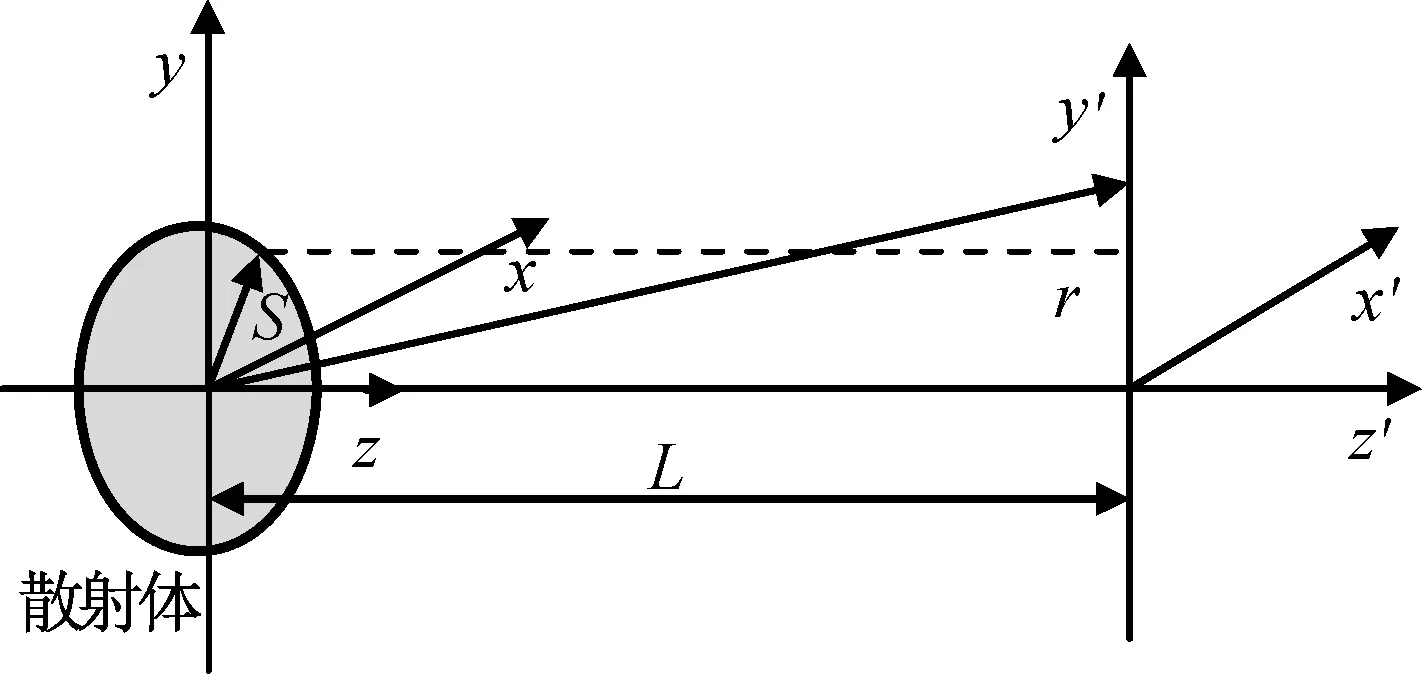
圖1 散射示意Fig.1 Scatter on plane

將式(8)轉(zhuǎn)為柱坐標(biāo)系，當(dāng)光場(chǎng)傳輸路徑遠(yuǎn)大于散射體半徑時(shí)近似有

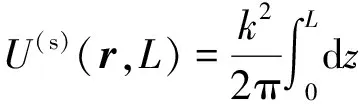
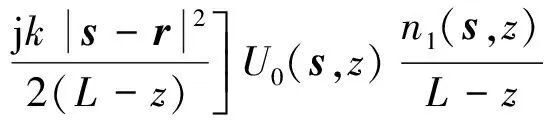
(9)

式中：

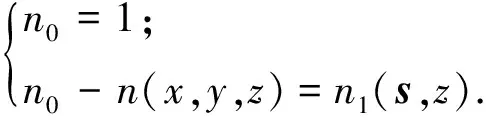
(10)

當(dāng)光場(chǎng)傳輸路徑遠(yuǎn)大于散射體范圍時(shí)，有

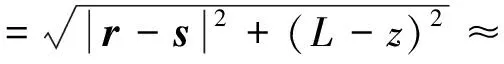
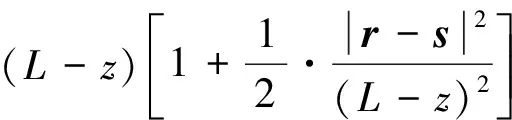
(11)

將式(11)代入式(9)，可得散射場(chǎng)分布為

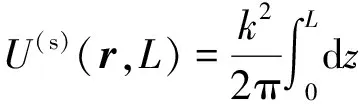
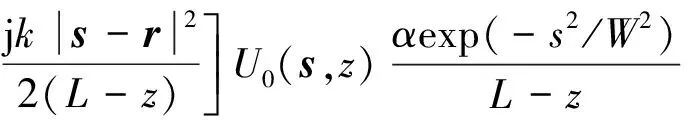
高職英語(yǔ)的職業(yè)教育目標(biāo)是“以服務(wù)為宗旨，以就業(yè)為導(dǎo)向”，體現(xiàn)以人為本，以學(xué)生為中心，注重培養(yǎng)學(xué)生的語(yǔ)言應(yīng)用能力，特別是聽(tīng)說(shuō)能力，同時(shí)培養(yǎng)高職學(xué)生綜合素質(zhì)，提升職業(yè)可持續(xù)發(fā)展能力。以此目標(biāo)，我們貫穿“1+X”的教學(xué)理念，實(shí)施“基礎(chǔ)英語(yǔ)+行業(yè)英語(yǔ)”的課程結(jié)構(gòu)體系和“分級(jí)教學(xué)”的立體教學(xué)體系。

(12)

式中：U0為光場(chǎng)在自由空間中傳播的復(fù)振幅。

玻恩一階散射近似在非常近距離的散射場(chǎng)計(jì)算中有良好的近似，但對(duì)距離較遠(yuǎn)的光傳輸特性，散射場(chǎng)將會(huì)發(fā)散[12]。因此，本文用Rytov散射近似。總光場(chǎng)可表示為

U(r,L)=U0(r,L)exp[ψ(r,L)]=

U0(r,L)[1+Φ1(r,L)].

(13)

式中：ψ(r,L)為光場(chǎng)調(diào)制函數(shù)。對(duì)一階Rytov散射近似，有

ψ(r,L)=ln[1+Φ1(r,L)]≈Φ1(r,L).

(14)

根據(jù)式(13)，一階玻恩散射近似后有

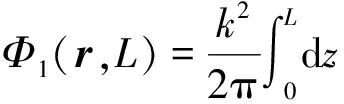
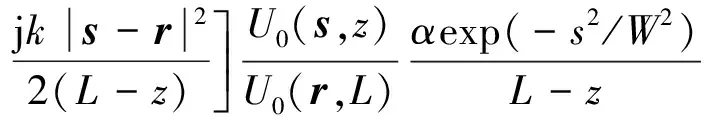
(15)

在自由空間中，基模激光傳輸方程可表示為

U0(r,L)=

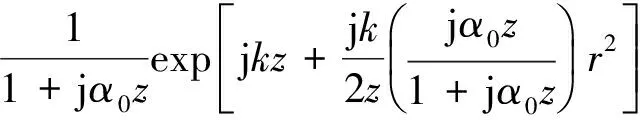
(16)

將式(16)代入式(15)，可得

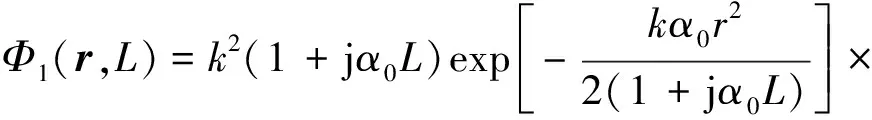
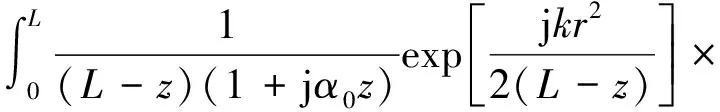
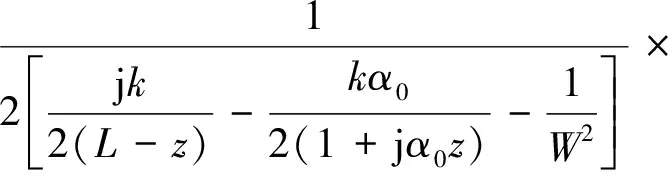
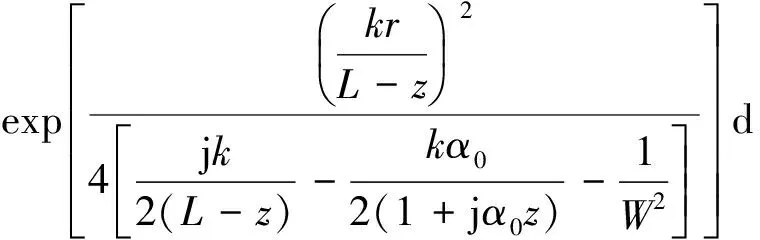
(17)

2 仿真與分析

設(shè)流場(chǎng)形成的高斯渦旋半寬度W=10 mm，激光光束腰束寬度W0=3 mm，激光在出瞳位置處被準(zhǔn)直，即在z=0平面上激光曲率半徑F0=∞，激光分別經(jīng)過(guò)傳輸距離0.1，0.5，1.0，2.0，3.0，4.0，5.0，10.0 m后，有無(wú)流場(chǎng)擾動(dòng)的仿真結(jié)果分別如圖2～9所示。

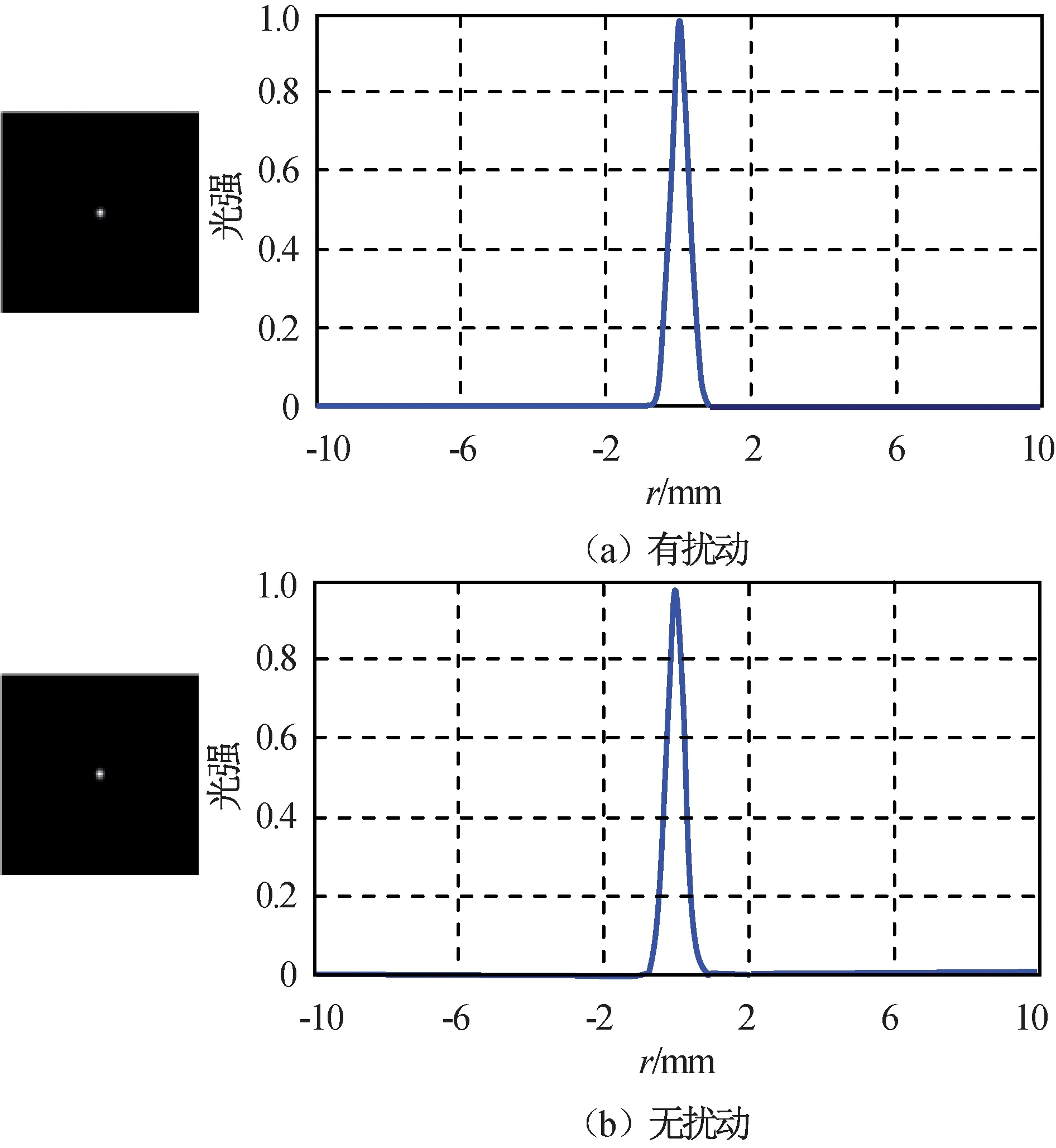
圖2 距離0.1 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.2 Spatial intensity distribution of laser light field under distance 0.1 m

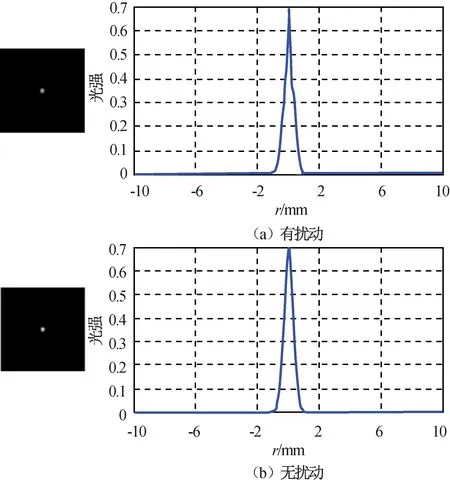
圖3 距離0.5 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.3 Spatial intensity distribution of laser light field under distance 0.5 m

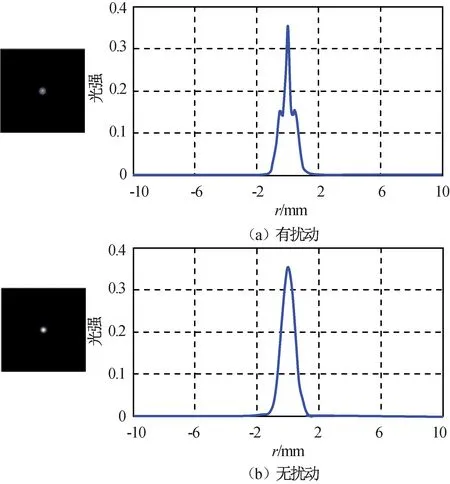
圖4 距離1.0 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.4 Spatial intensity distribution of laser light field under distance 1.0 m

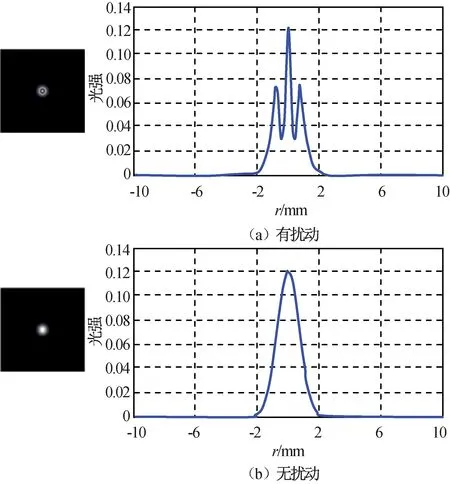
圖5 距離2.0 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.5 Spatial intensity distribution of laser light field under distance 2.0 m

圖6 距離3.0 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.6 Spatial intensity distribution of laser light field under distance 3.0 m

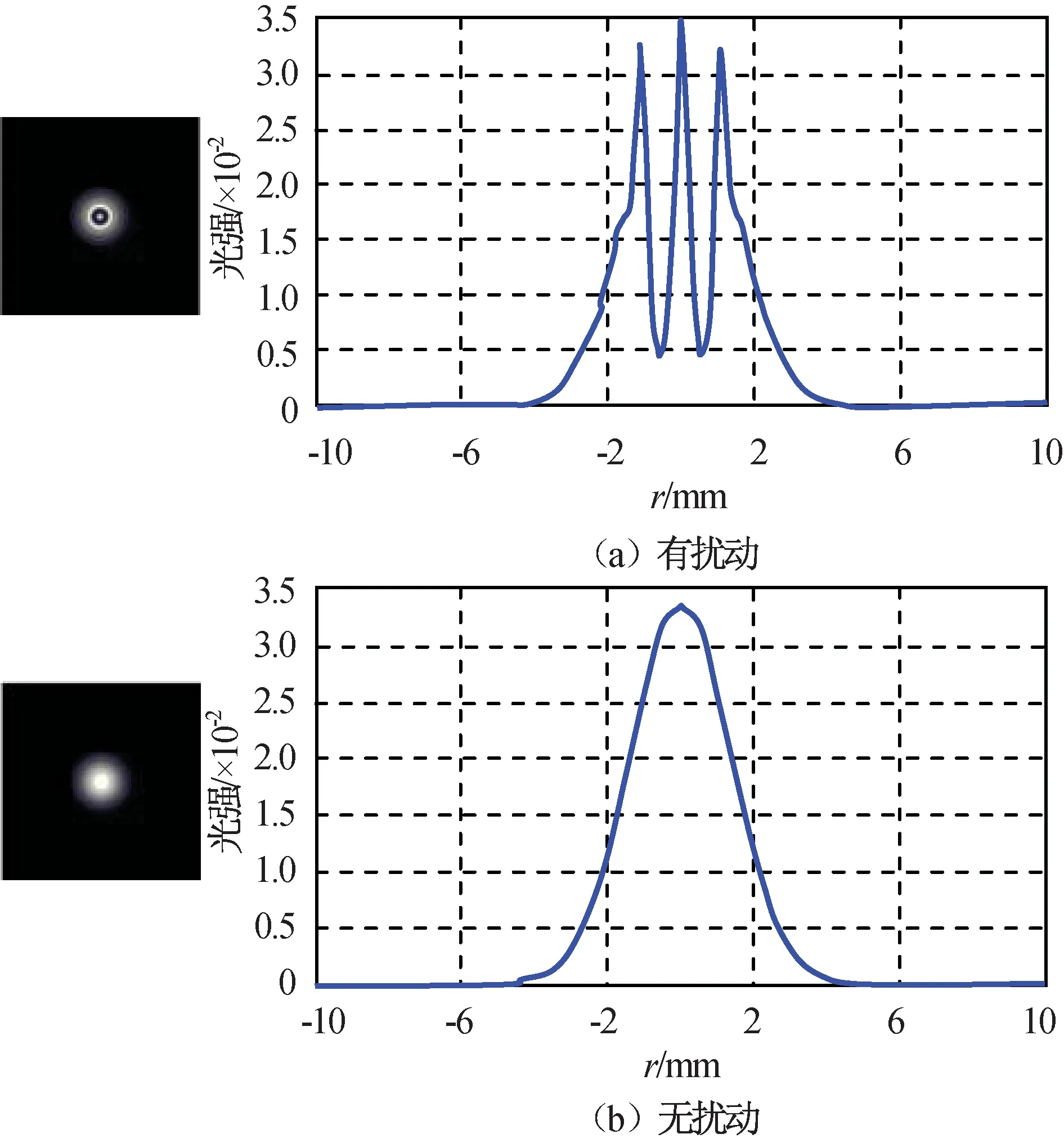
圖7 距離4.0 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.7 Spatial intensity distribution of laser light field under distance 4.0 m

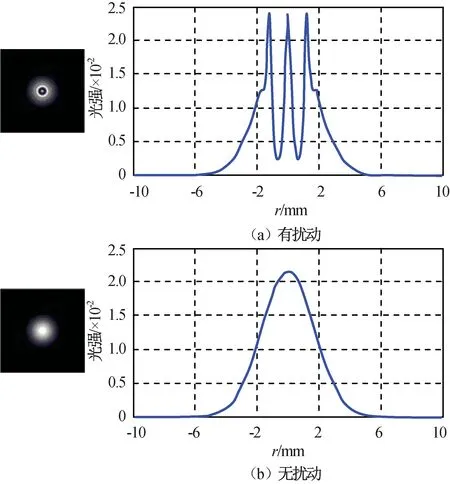
圖8 距離5.0 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.8 Spatial intensity distribution of laser light field under distance 5.0 m

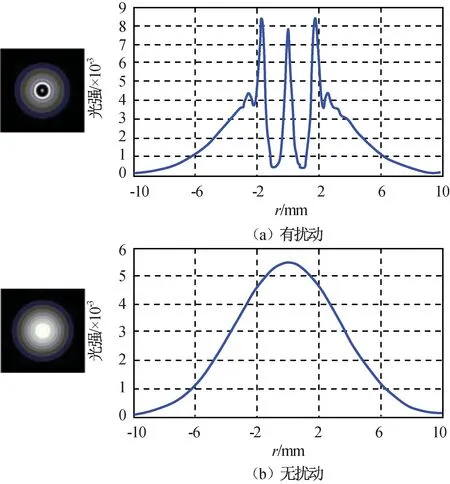
圖9 距離10.0 m時(shí)激光光場(chǎng)空間強(qiáng)度分布Fig.9 Spatial intensity distribution of laser light field under distance 10.0 m

由仿真結(jié)果可知：隨著激光傳輸距離的增加，激光光場(chǎng)的空間光強(qiáng)分布受到氣動(dòng)流場(chǎng)的調(diào)制，在中心光場(chǎng)1.0 mm處，光強(qiáng)急劇下降；有流場(chǎng)擾動(dòng)時(shí)，中心位置光強(qiáng)度與自由空間高斯光束傳輸中心位置光強(qiáng)相近，但在兩側(cè)會(huì)形成一個(gè)暗環(huán)，使激光光場(chǎng)的空間強(qiáng)度分布發(fā)生改變，導(dǎo)致激光脈沖光束出現(xiàn)形變。

3 結(jié)束語(yǔ)

本文針對(duì)單結(jié)構(gòu)渦旋，基于激光光束的傳輸過(guò)程，利用了玻恩散射積分方程構(gòu)建光場(chǎng)傳輸模型，由仿真結(jié)果可得以下結(jié)論：由于渦旋發(fā)展的周期性，估計(jì)其光學(xué)性質(zhì)在時(shí)間上有一定的周期性，可根據(jù)渦旋變化時(shí)域中的解析式推導(dǎo)光學(xué)性質(zhì)的時(shí)間變化。光場(chǎng)強(qiáng)度分布將產(chǎn)生極大的畸變，其演變過(guò)程是向中心高頻振蕩展開(kāi)的形式發(fā)展，導(dǎo)致光強(qiáng)的空間分布出現(xiàn)暗圈。由于單結(jié)構(gòu)渦旋是一種近似的替代，與真實(shí)的渦旋情況有差異，且在空間上是一種連續(xù)分布，不是一種周期性的分布。對(duì)流體仿真來(lái)說(shuō)，后續(xù)研究需模擬出一個(gè)渦旋發(fā)展周期內(nèi)數(shù)個(gè)典型流體場(chǎng)的特征，類(lèi)似于研究大氣湍流中光學(xué)，可更深入地研究光學(xué)性質(zhì)，如相干度、偏振態(tài)及偏振度的變化，以及光束的展寬、光斑的偏離和閃爍現(xiàn)象。

[1] Al Ma-ni, MENG Wang, MOIN P. Tatistical description of the free-space propagation of highly aberrated optical beams[J]. Optical Society of America, 2006(11): 3027-3035.

[2] TRUMAN C R. The influence of turbulent structure on optical phase distortion through turbulent shear flows[R]. AIAA, 92-2817, 1992.

[3] VILLARS F, WEISSKOPF V F. The scattering of electromagnetic waves by turbulent atomospheric fluctuations[J]. Physical Review, 1954(4): 232-240.[4] COLONIUS T, LEE S K, MOIN P. The free compressible viscous vortex[J]. Fluid Mech, 1991, 230: 45-73.

[5] TROMEUR E, GARNIER E, SAGAUT P. Large-eddy simulation of aero-optical effects in aspatially developing turbulent boundary layer[J]. Journal of Turbulence, 2006(1): 1-8.

[6] 馬小亮, 楊國(guó)偉, 申義慶. 可壓縮渦中的激光傳播[J]. 計(jì)算物理, 2008, 25(5): 602-606.

[7] TROLINGER J D, ROSE W C. Technique for simulation and evaluation aero-optical effects in optical systems[R]. AIAA, 2005-4654, 2005.

[8] 史可天, 馬漢東. 基于渦球模型的湍流氣動(dòng)光學(xué)效應(yīng)預(yù)測(cè)方法[J]. 紅外與激光工程， 2012, 41(6): 1401-1404.

[9] 房建成, 楊照華, 吳琳. 基于渦結(jié)構(gòu)的氣動(dòng)光學(xué)傳輸效應(yīng)研究[J]. 紅外與激光工程, 2006, 35(S1): 372-379.

[10] CICCHIELLO J M, JUMPER E J. Far-field optical degradation due to near-field transmission through a turbulent heat jet[J]. Optical Society of America, 1997(8): 6411-6452.

[11] BORN M, WOLF E. Principles of optic[M]. London: Cambridge, 1999.

[12] ANDREW L C. Laser propagation in the random media[M]. San Francisco: SPIE, 2005.

Research on Laser Transmission Characteristic with Single Vortex

XU Ling-fei, BI Peng, ZHOU Zhi-chao, REN Tian-rong

(Shanghai Electromechanical Engineering Institute, Shanghai 201109, China)

The laser transmission characteristic with single vortex was studied in this paper. The whole flow field was broken down into several individual units and the refractive index of each unit was uneven. The Maxwell integral equation was used to replace differential equation to solve the flow field of the optical field distribution. The computation model of the refractive index of pneumatics vortex was given out. When there was only one ideal vortex flow field and eddy current of refractive index had approximate analytic form, the integral equation was used to calculate the flow filed disturbance by Rytov scatter approximate based on scattering theory of non-uniform medum scattering tueory. The spatial intensity distribution of light field within disturbance under various laser transmission distance was discussed. It was found that the light intensity would decrease greatly as the distance increasing, and the light intensity at centre was similar to the one of free spatial Gauss beam transmission at centre without disturbance but a dark ring would be formed at both sides which could make spatial light distribution of laser field changed and result in deformation of laser pulse beam. The study demonstrated that the integral equation was used to describe pneumatic optical effect was feasible, and it provided a new way for the precise calculation of complex vortex field structure.

Laser transmission; Maxwell integral equation; Pneumatic optical effect; Gauss vortex; Refractive index; Spatial intensity; Flow field disturbance; Transmission distance

1006-1630(2016)04-0010-06

2016-02-15；

2016-03-16

上海市揚(yáng)帆計(jì)劃資助(15YF1405600)

許凌飛(1984—)，男，博士，高級(jí)工程師，主要從事戰(zhàn)術(shù)導(dǎo)彈紅外制導(dǎo)設(shè)計(jì)。

TN241

A

10.19328/j.cnki.1006-1630.2016.04.002