運用質心系解決兩體碰撞問題

蔡支坤 王笑君

(華南師范大學物理與電信工程學院 廣東 廣州 510006)

?

運用質心系解決兩體碰撞問題

蔡支坤 王笑君

(華南師范大學物理與電信工程學院 廣東 廣州 510006)

將以質心坐標系為橋梁解決兩體碰撞問題.先推導出兩物體碰撞前的速度在質心系中的表達，然后推導出兩物體碰撞后速度在質心系中的表達，最后運用相對性原理計算出兩物體碰撞后速度在一般慣性參考系中的表達，從而建立起了兩物體碰撞后速度與碰撞前速度的直接聯系.

質心系 兩體碰撞 慣性系

1 研究的背景

兩體碰撞是物理教學和理論研究中常見的一類問題，是研究運動的物體相互作用的最簡單模型，也是質點運動學中非常重要的內容.對此問題，傳統的解法是對兩個物體碰撞前后的動量和能量進行分析，列出方程進行計算，原則上可以解出最后結果，但是此方法因為涉及到二元二次方程，計算過程顯得繁瑣，且容易出錯.本文另辟蹊徑，以質心坐標系為橋梁，并結合坐標圖像，建立起兩物體碰撞后的速度與碰撞前速度的聯系，并將最后的計算結論推廣到一般的情形中.較之于傳統的解法，此種方法避免了復雜的計算，在熟悉了推導過程后，可以直接將最后的計算結果運用到所有的一維碰撞過程中.

2 質點組和質心系

對于單個質點的受力和運動情況的研究，相信讀者已經比較熟悉，而對于存在相互作用的多個質點的運動情形，情況看起來要復雜一些，為此，我們引入質點組的概念，把由許多(有限或無限)相互聯系著的質點所組成的力學體系叫做質點組.

在對整個質點組運用動力學基本定理時，我們發現：在質點組中恒存在一特殊點，它的運動很容易被確定.如果以這個特殊點作為參考點，又常能使問題簡化，我們把這個特殊點叫做質點組的質量中心，簡稱質心C.

現說明這個特殊點的位置是如何定出的[1].

假定有n個質點，它們的質量是m1,m2,…,mn,位于P1,P2,…,Pn諸點，這些點相對某一指定的參考點O的位矢是r1,r2,…,rn，則質心C對同一點O的位矢rC滿足以下關系

此即為質心C相對于參考點O的位矢，以質心C為原點建立的坐標系稱為質心坐標系，簡稱質心系KCM.

3 兩物體碰撞前在質心系中的速度

兩個質點組成最簡單的質點組，如圖1所示，以O為坐標原點的慣性參考系稱K系，設質點1和2碰撞前在K系的位矢分別為r10，r20，相對位矢為

r0=r10-r20

進而可以得到質點1和2碰撞前在K系中的速度分別為

圖1

引入相對速度的概念，在K系中兩質點碰前的相對速度為

點C為質點1和2的質心，則質心C應在兩質點的連線上，根據質心位矢的定義，質心C相對于K系的位矢為

則質心C相對K系的速度vC為

結合相對運動的相關知識以及上面的坐標圖像，可以建立兩質點的位矢和速度矢量在K系和質心系KCM之間的聯系.

位矢之間的關系為

上邊兩式同時對時間進行求導，可以得到速度之間的關系如下

將上邊兩式相減得到

(1)

由此我們可以看到，兩質點在K系中的相對速度與兩質點在質心系KCM中的相對速度相等，也就是說，兩質點之間的相對速度與參考系無關.

下面來計算一下兩質點在質心系KCM中的總動量

(2)

從上述結果我們可以看出兩質點在質心系KCM的總動量為零，不難證明，對于多個質點組成的質點組的情況，該結論仍然成立，因此我們經常將質心系又叫做零動量系或者動量中心系[3].

結合上述相對速度式(1)和總動量為零的式(2)，可以得到質點1和2在質心系KCM的速度為

因此，結合坐標圖像和相對運動的知識，我們就得到了質點1和2碰前在質心系KCM中的表達式.

4 兩物體碰撞后在質心系中的速度

本文主要討論比較常見的對心碰撞，在對心碰撞中，兩質點具有相對于質心的點對稱性，那么兩質點在碰撞前后所有速度方向都沿兩質點連線方向，據此，我們可以作出碰撞之后的坐標圖像.

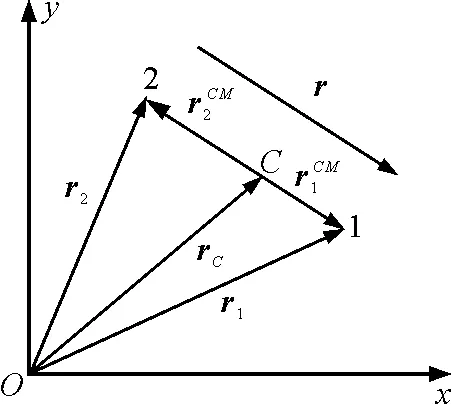
圖2

如圖2所示，碰撞后與碰撞前相比，質點1和2關于質心C點對稱，此時，質點1和2在K系中的位矢分別為r1，r2，速度分別為

兩質點之間的相對位矢為

相對速度為

容易證明，兩質點碰撞之后在質心系KCM中的總動量也為零，因此兩質點碰后的計算與兩質點碰前的計算類似，可以得到質點1和2碰撞后在質心系KCM中的速度分別為

因此，根據對心碰撞的點對稱性以及結合圖像可以快速地得出兩質點碰后在質心系KCM中的表達式.

5 兩物體碰撞前后速度的聯系

在任何短暫的碰撞過程中，物體之間的內力遠遠大于外力，因而總可認為，碰撞過程中系統的總動量是守恒的，因此可以得到

m1v10+m2v20=m1v1+m2v2

所以，碰撞前后質心C在K系中的速度相等

即碰撞前后質點組的質心速度保持不變.

牛頓總結了各種碰撞實驗的結果，引進了恢復系數e的概念[2]，它定義為

根據點對稱性，在質心系KCM中，碰撞前的相對速度和碰撞后的相對速度方向彼此相反，因此有u=-eu0；利用此式，我們可以建立碰撞前后質點組相對于質心系的速度關系如下

因為碰撞前后，質心C的速度vC保持不變，所以根據伽利略相對性原理，碰撞后質點1和2在K系中的速度分別為

再將相對速度的表達式代入上式，就可以得出兩質點碰撞后質點的速度與碰撞前速度的關系

我們來看看該結論在兩類常見碰撞情況中的運用.

(1)完全彈性碰撞，e=1

m1v10+m2v20=m1v1+m2v2

聯立上述兩式或直接將e=1代入，可以得到碰后兩質點的速度為

(2)完全非彈性碰撞，e=0

v1-v2=0

m1v10+m2v20=m1v1+m2v2

聯立上述兩式或直接將e=0代入，可以得到碰后兩質點的速度為

6 小結

行文至此，本文利用質心坐標系和坐標圖像法解決了一般的對心碰撞問題.上述推導過程看似復雜，其實非常有規律可循，一步一步推導下來非常嚴謹.再結合質點的位矢坐標圖像，不僅可以幫助檢驗計算的結果，還有助于理解相關的計算結果，避免死記硬背.運用質心系的優越性就在于其對稱性，質點組相對于質心系的總動量為零，以質心系為橋梁，可以很好地建立兩物體在碰撞前后速度的關系，簡化計算.希望本文能為廣大師生解決兩體碰撞問題提供一些幫助.

1 周衍柏.理論力學教程.北京：高等教育出版社,2009. 84～852 趙凱華，羅蔚茵. 新概念物理教程:力學.北京：高等教育出版社,2004. 127～130

3 馮奇勝.質心參照系中兩體碰撞問題的研究.物理通報，2001(6)：14～15

2015-10-13)