內生性回收率與信用風險度量研究
吳建華,王新軍,張 穎
(1.濟南大學數學科學院, 山東 濟南 250022; 2.山東大學經濟學院, 山東 濟南 250100)
?
內生性回收率與信用風險度量研究
吳建華1,王新軍2,張 穎1
(1.濟南大學數學科學院, 山東 濟南 250022; 2.山東大學經濟學院, 山東 濟南 250100)
在信用風險模型中,外生性回收率的設定會忽略回收率對損失分布尾部的影響,而且會導致潛在的模型風險。本文將因子擴散過程引入結構信用風險模型,獲得了回收率和違約概率之間的內在關系,利用Monte Carlo模擬方法數值分析了預期回收率對違約概率和資產價值波動率的依賴性,結果表明預期回收率與違約率之間具有很強的負相關關系,而且這種相關關系會受到債務人資產價值波動率的正向影響。在內生性回收率下,推導了信用損失的概率分布,計算了信用風險的Credit-VaR和ETF指標。最后利用市場數據檢驗了內生回收率信用風險模型的有效性,結果表明該模型可以很好的描述歷史違約率和回收率的變化過程。
內生性回收率;因子擴散過程;信用風險度量;數值模擬;實證檢驗
1 引言
對金融機構、金融監管和債權人來說,信用風險度量一直是最為核心的內容。尤其是對于結構化信用衍生產品的定價和信用評級,信用風險的度量更是一個基本的前提條件。然而,目前大多數現代信用風險度量模型主要是圍繞違約概率展開,對于違約回收率的研究相對較少,從技術層面來看,違約概率的建模比較容易處理,而回收率的建模需要考慮更多的影響因素,比如借款人的信用質量、債項的特征(債務工具優先級)、抵押品質量、行業分類、宏觀經濟因素等的影響。在信用風險管理中,違約回收率用來描述違約發生時債權人資產回收的程度。在商業銀行內部評級高級法中,預期損失與非預期損失的計算以及對信貸業務的風險調整度量都需要估計回收率風險。同樣,在信用衍生產品和結構化信用產品的定價計算中,也必須對標的資產回收率進行估計。
縱觀信用風險度量模型的研究,主要以回收率的外生假設為主。從結構化模型來看,雖然Merton[1]在第一次提出結構化信用風險模型時,就指出違約概率和回收率均由到期時企業的市場價值決定,但是Merton對于市場價值如何影響回收率的機制并沒有做進一步的說明。而且,在Black和Cox[2]將Merton模型推廣到首達時模型時,回收率不再設定為由企業市場價值決定,而是被獨立的模型化的,它被定義為未償付債務價值的固定比率,而且與違約概率相互獨立。之后的研究基本上是以外生性回收率作為前提,只是具體假設有所差異,比如Jokivuolle和Peura[3]的研究中假設外生的抵押品的價值是決定回收率的唯一隨機因素。Giesecke[4]的研究中回收率則直接被假設為常數,Asvanunt 和Staal[5-6]的研究中回收率是由一個簡約化的方法決定的。總之,絕大多數結構化模型中,無論回收率被直接假設為常數,還是決定于某些因素,都是以回收率的外生性為特征的。
從信用風險度量的另一個路徑——簡約化模型來看,回收率則徹底被外生化。Jarrow和Turnbull[7]首次建立了一個離散形式的簡約化模型,隨后在Jarrow等[8]、Duffie和Singleton[9]的研究基礎上發展形成了簡約化信用風險模型,在所有的簡約化模型中,只有在為了計算信用損失分布和進行資產定價的時候,才考慮回收率的問題。簡約化模型對回收率的處理方式可以概括為三種:等價回收率、市值比例回收率和面值比例回收率。Jarrow和Turnbull[1]假設當違約發生時,債權人可以獲得固定比例的等價面值無違約風險的零息債券。Duffie和Singleton[9]假設回收部分的價值與債券違約前的市場價值保持一個恒定的比率。Houweling和Vorst[10]將回收率看做違約債券面值的一部分。違約發生時,債權人可獲得基于面值的恒定比率的現金償還。這三種方法各具特點:等價回收率的形式更適合適用于公司債券;市值比例回收率的假定符合互換合約的結構且易于拓展。面值比例回收率可以簡化模型在計算方面的復雜性。
另外,從信用風險的應用模型來看,四大現代信用風險度量應用模型Credit Metrics、KMV、Credit Portfolio View和Credit Risk Plus中的違約回收率通常被看作是外生的常數或隨機變量,而且回收率和違約概率被看作兩個獨立變量。關于外生性回收率分布的假設,Frye[11]建立了回收率的正態分布模型,Pykhtin[12]提出對數正態分布模型,Andersen和Sidenius[13]討論了正態模型、log正態模型、probit正態模型和logit-正態模型進行了對比研究。黃大海[14]對四種經典的應用模型的回收率情況進行了總結,說明了Credit Metrics、KMV和Credit Portfolio View中的回收率通常假定服從單峰Beta分布,與違約概率互不相關,Credit Risk+模型中的回收率則被假設為常數。王國棟和詹原瑞[15],汪飛星和姚磊[16]則進一步建立了回收率的雙峰Beta分布密度模型。陳暮紫等[17]利用廣義Beta回歸對影響不良貸款回收率的因素進行了實證分析,給回收率的實證研究提供了一個很好的計量經濟學分析框架。
關于回收率和違約概率之間的相關性關系實證研究方面存在一定的爭議。對于債券來說,Carty等[18]、Frye[19],Bakshi等[20],Hu和Perraudin[21],Cantor等[22],Carey和Gordy[23]以及Altman等[24]的研究發現對于企業債券來說,回收率與違約概率之間存在負相關關系。對于貸款來說,由于抵押品的存在,只要抵押品的價值相對穩定,即使由于外在經濟環境的影響導致違約概率上升,貸款的回收率也可能不會下降。但是Hamilton[25],Hu Yen-ting 等[26]通過實際的數據研究顯示,當總的貸款違約概率較高時,回收率與違約概率之間還是存在一定的負相關性。 對于信用衍生產品來說,Hull和White[27]研究表明,衍生品CDO和CDS的隱含回收率與PD之間都存在顯著的負相關關系。Das和Hanouna[28]利用 CDS價差數據進行了實證分析,發現隱含回收率和PD呈負相關關系,尤其在PD很高時,這種負相關性更加明顯。
綜上所述,在信用風險度量模型中,有關回收率的研究主要集中于回收率的影響因素、回收率的分布模型、回收率與違約率的相關性等方面。目前的研究主要包括兩個方面的不足,一是回收率的外生性假設。絕大多數信用風險模型普遍假設回收率與違約概率相互獨立,實證研究表明這會嚴重低估實際的巨額損失。而且這種主觀的假設會導致潛在的模型設定風險;二是回收率分布的假設,多數模型假設回收率服從貝塔分布。但是實證研究顯示,基于貝塔分布的信用VaR估計的誤差有增大的趨勢。
然而,無論是從經濟學直覺還是從金融實踐來看,違約資產的回收率都不應該是外生的,事實上,如果某項資產在違約之后具有較低的回收率,那么這就意味著該項資產必然具有較高的違約率,反之,較高的回收率必然意味著債務人的以及債項的信用質量較高,在正常的經濟環境下,不會輕易的發生違約。實際上,從大量關于回收率的實證研究來看,違約概率和回收率之間不是相互獨立的。
從上面這些文獻可知,無論是債券、貸款還是信用衍生品,回收率和違約概率之間都存在明顯的負相關關系。但是以上這些文獻只是說明了回收率和違約概率之間的負相關關系,并沒有具體說明這種負相關關系之間的內在機理。為此,需要考慮如何將回收率進行內生化分析。目前關于這方面的研究還較少,僅有的文獻有,Guo Xin等[29]提出在傳統簡約模型的框架中加入一個反映回收率的隨機過程。模型中公司違約過程、回收率過程和風險債務定價的定量化都是基于公司的資產價值。Chava等[30]提出,在簡約模型中假設違約概率和回收率同時依賴于單一的公共因子,從而保留了違約和回收率之間的負相關,但是該模型的缺點是待估參數過多,而且有些參數從經濟學的角度難以解釋。不過,以上這兩篇文章對于回收率內生化的研究,主要是在簡約模型框架內進行的,對于結構模型框架內的回收率內生化機理的研究還是個空白。
Merton曾提出違約概率和回收率均由到期時企業的市場價值決定。但是Merton對于市場價值如何影響回收率的機制并沒有做進一步的說明。本文在結構模型框架內,研究了多資產內生性回收率的機理,在假設信用資產服從因子擴散過程的假設下,推導了回收率和違約概率之間的內在函數關系,該函數關系僅僅依賴于一個參數,我們稱之為內生回收率。內生回收率在保持違約率同回收率之間的負相關關系的前提下,避免了外生性回收率假設所存在的潛在的模型風險。在內生回收率框架內,推出了信用損失的概率分布,計算了兩個重要的信用風險度量指標C-VaR和ETF。利用Monte Carlo模擬數值分析,檢驗了內生回收率的有效性。最后,利用Moody公司的部分數據,檢驗了本文模型的有效性。
2 回收率的內生性分析
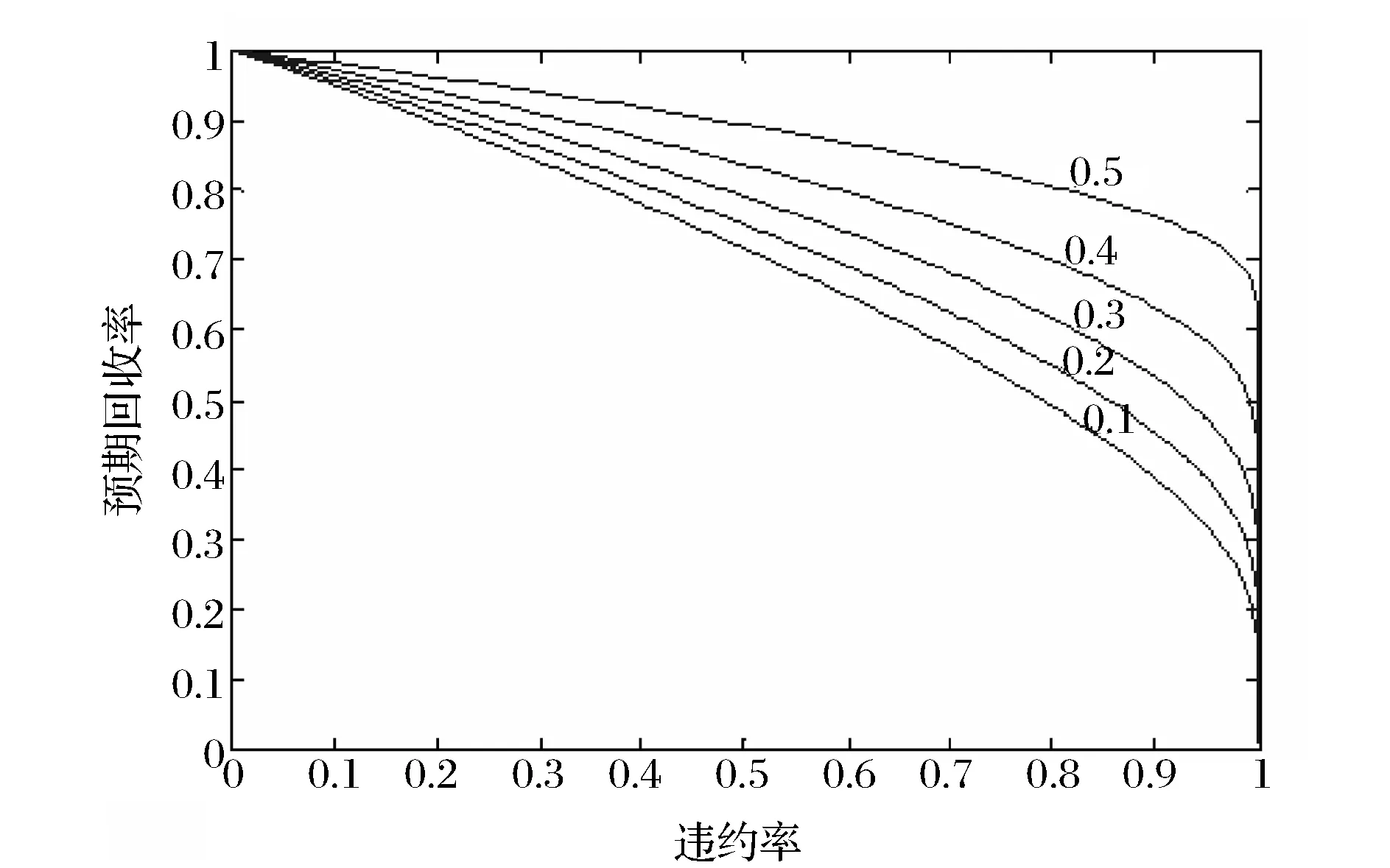
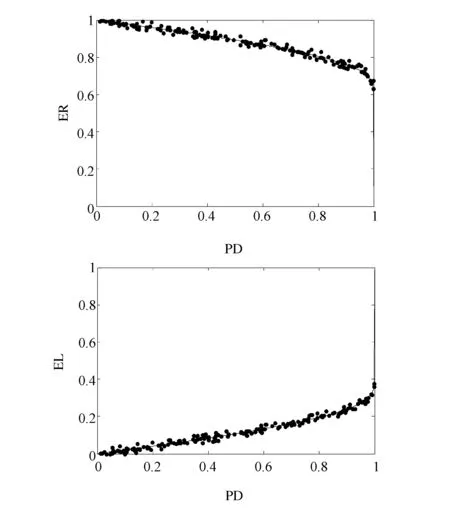
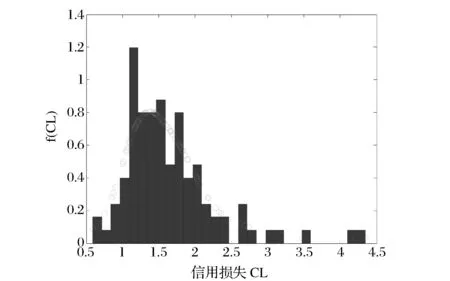
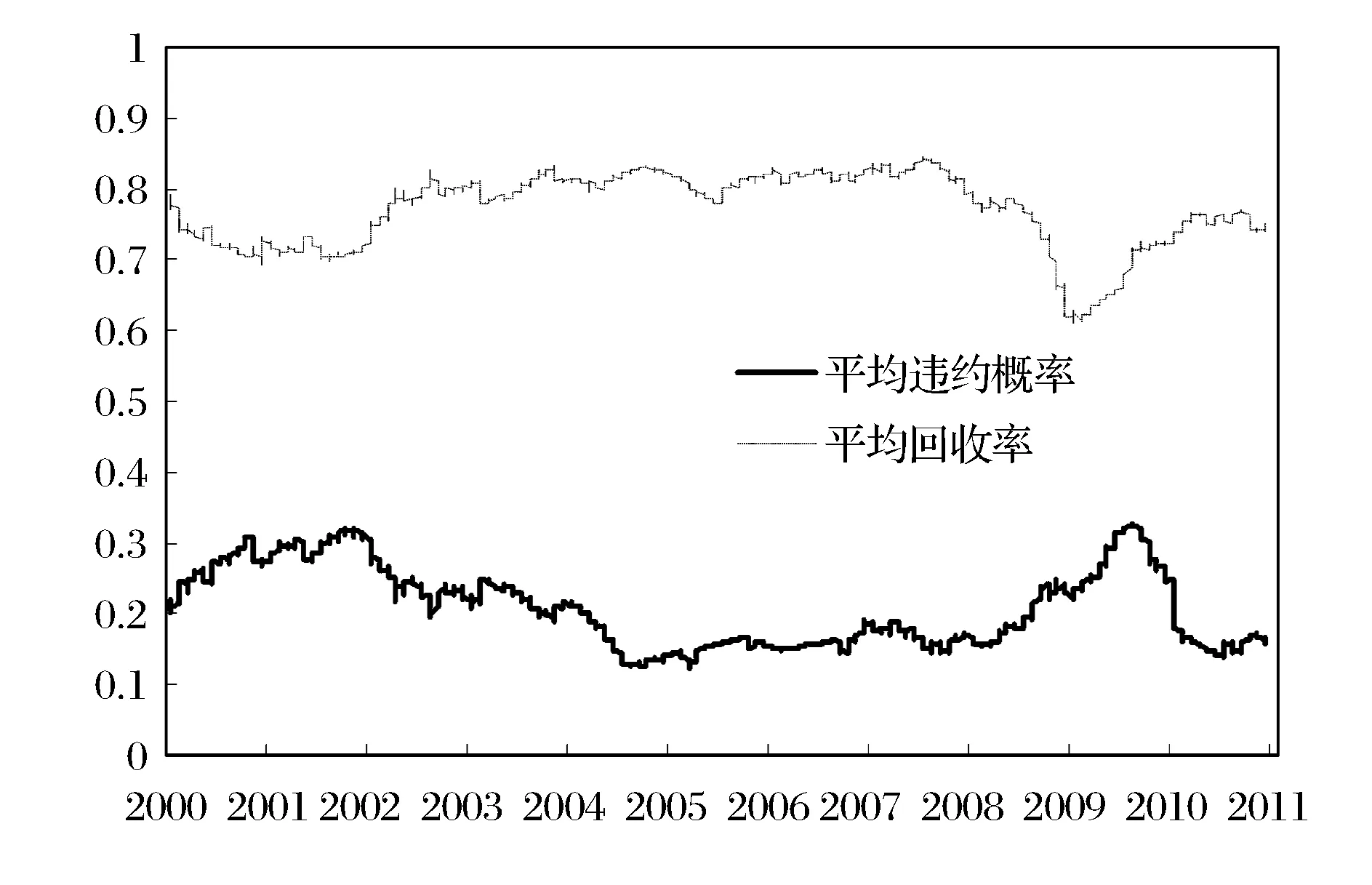
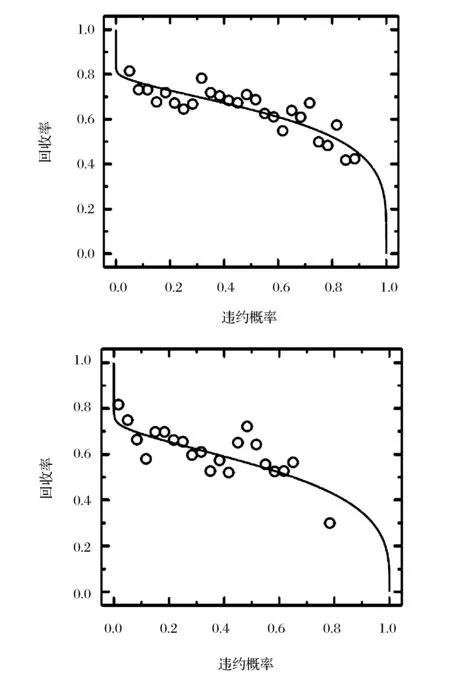
考慮具有K個企業的債務組合,企業k(k=1,…,K)的市場價值為Vk。出于分析的簡化,假設企業資產結構由所有權益和負債組成,企業k發行一種特定的零息債券,該債券的面值為Fk=F,持有期為T。假設企業資產市值的初始值為Vk(0)=V(0)。當企業資產價值在T時刻低于面值,即Vk (1) 令fVk(v)表示在到期日T,企業k的市場價值Vk的概率密度函數。那么違約概率為: (2) 預期回收率為: (3) 由(2)(3)式可知,違約率和回收率都是由T時刻企業的資產價值Vk決定的。從(3)可以看出,預期回收率E(Rk)受到違約率PD,k的直接影響,同現有的大多數信用風險模型中兩者是獨立的假設相比,違約率和回收率之間的這種函數關系更貼近實際情況,我們稱之為內生性回收率。值得一提的是,本文突出了回收率的“內生”特征,這一點從式子(1)和(3)中可以清楚的看到,無論是回收率Rk還是預期回收率E(Rk)都是資產價值Vk的函數,這是同已有的外生性回收率的設定本質不同的地方,而三種常見的外生性回收率:等價回收率、市值比例回收率和面值比例回收率的設定都是在債權債務契約簽訂之前就外生設定的,而與債務契約簽訂之后的資產的價值是沒有任何關系的。 3.1 企業價值的因子擴散模型 在經典的結構模型中,通常假設企業的市場價值V(t)服從下面的擴散過程: dV(t)=V(t)μdt+V(t)σdZ (4) 其中μ為漂移項,σ為波動項,dZk服從標準布朗運動。但是,這種經典設定沒有說明造成市場價值波動的原因。從經濟學常識我們可知,影響市場價值波動的原因無非來源于兩個方面,一是系統性的宏觀經濟環境的改變;二是非系統性的個別企業內部經營管理的微觀層面的變動。因此,在擴散過程中引入公共的宏觀經濟因子和企業自身的特殊因子,可以更好的刻畫企業價值的變化。另外,在信用資產組合中,不同企業之間的相關性也會影響到整個資產組合價值的變動,表現為企業之間的違約相關性,通過因子模型可以方便的描述不同企業之間的交互作用,這種相關性的描述在經典的Merton模型中沒有給出。 假設企業k(k=1,…,K)的市場價值Vk是由公共的宏觀經濟因子M和個別企業的特殊因子Zk所決定的,即: (5) 其中M和Zk均服從標準正態分布,Zk,k=1,…,K之間相互獨立,每一個Zk與M也相互獨立。c∈[-1,1]為常數,這意味著,任何兩個企業之間的具有相同的相關結構。這樣,我們就可以假設企業k的市場價值Vk(t)在t時刻的變動過程服從下面的隨機微分方程: (6) 上式描述了一個具有線性相關特征的因子擴散過程,μ為漂移項,σ為波動項和c為相關系數。dM和dZk分別表示市場的波動性和企業k的波動性,都服從標準維納過程。顯然,由(6)式可知,不同的宏觀經濟變量M和企業的特殊狀況Zk的實際值,會形成不同的市場價值Vk的概率密度函數fVk(v),從而根據(2)(3)我們可以計算得到不同的違約概率PD,k和預期回收率E(Rk)。 3.2 內生回收率的理論分析 把債券的期限T等分為N段,Δt=T/N為離散時間的增量,這樣我們就可以得到(6)式的離散形式,對任意的t∈[0,T]: (7) 其中η和εk均為標準正態分布,分別表示來自市場方面的隨機沖擊和企業自身經營的不確定性帶來的沖擊。對(7)利用迭代運算可得在到期日T,企業k的市場價值服從如下的規律: (8) 令Xk=(Vk(T)-V(0))/V(0)為企業k的市場收益率,所有K個企業在[0,T]內的市場平均收益率記為Xm,則: (9) (10) (11) (12) 對于企業k,利用(8)(9)(11)我們有: (13) (14) (15) 由此可以得到單個企業的違約概率如下: (16) (17) 企業的平均違約損失L=1-V/F的期望值可以如下計算: (18) 從而有: (19) 根據(17)我們可以將A(Xm)表達成PD的函數: (20) 這樣,我們就可以得到預期回收率和違約概率的函數依賴關系: (21) 這就是內生性回收率如何受到違約概率影響的內在機理。此外,從方程(21)還可以看到預期回收率與違約率的函數關系受外生變量B的結構性影響。為了更加直觀的理解這一關系,在圖1中給出不同的波動率下B,違約概率對預期回收率影響的變化情況。 圖1 不同波動率下,違約概率對預期回收率的影響,B=0.1,0.2,0.3,0.4,0.5 由圖1可知,隨著違約概率PD的增加,預期回收率對違約概率變得更加敏感,當違約概率足夠大,趨向于1時,預期回收率會迅速趨向于0,表明預期回收率對違約概率具有高度的負的依賴性。另外,債務人資產的波動性B越高,預期回收率E(R(PD))就整體越高,表明資產價值的波動性不但影響違約概率,對于回收率的整體變動具有系統性的影響,并且表現出較強的正相關性。無論是違約概率還是波動性,它們都對預期回收率具有內在的影響。這充分說明,回收率不應該被人為地設定為外生的,回收率的外生性設定會帶來嚴重的模型風險。 3.3 對內生回收率的數值分析 在MC模擬中,我們考慮了方程(8)中的離散時間隨機過程。由于我們只考慮在T時刻的債務的市場價值,因此在進行模擬時,我們直接取了一大步,即Δt=T,故N=1。因此,市場價值的離散形式為: (22) 每次給定一個市場波動的實現值η,我們模擬K=5000次得到5000個不同的εk實現值。對于每一次模擬的運行,我們計算市場平均收益率Xm,違約概率PD(Xm)和預期回收率E(R(Xm))。市場平均收益率Xm被定義為到期日T時刻的平均收益: (23) 對于足夠大的K來說,異質項εk會達到平均水平,而市場平均收益率Xm由η的實現值單獨的定義。這就是為什么我們利用市場平均收益率作為其他觀測值的參數的原因。對于違約概率做如下估計: PD(Xm)≈ND(Xm)/K (24) 其中ND(Xm)是違約次數,取值為事件Vk(T) (25) 進而得到預期損失率: (26) 從而可以估計預期回收率為: E(R(Xm))=1-E(L(Xm)) (27) 這里,我們假設違約的次數嚴格的非零,這對于足夠大的組合規模K來說是合理的。對市場平均收益率項的實現值模擬106次,這樣我們就可以得到市場平均收益率Xm,違約概率PD(Xm)和預期回收率E(R(Xm))的不同的值。 不失一般性,假設市場價值的初始值為V0=100,零息債券的面值為F=75,到期日為T=1(比如1年)。相關系數假設為c=0.5,這同股票價格的常見的相關性是一致的。擴散過程的參數設為μ=0.05,σ=0.15,這意味著每年的平均增長率5%和波動率15%。對應的杠桿率F/V0=75%。帶入(22)可得: 模擬結果畫在圖2中,同時給出了預期回收率和預期損失率對違約概率的依賴性。 圖2 預期回收率ER和預期損失率EL對違約概率PD的依賴性 在圖2中,左圖顯示了預期回收率E(R(Xm))對違約概率PD(Xm)的依賴性,右圖顯示了預期損失率E(L(Xm))對違約概率PD(Xm)的依賴性,其中紅色的散點表示MC模擬結果,藍色的線表示分析結果。分析結果中的波動性B是由模擬結果獲得的參數。在這兩個例子中,我們分別觀察到了在MC模擬和方程(21)中的分析結果之間的高度的一致性。而且對于高違約概率,對于均值的偏離是較小的。這一點同實際的回收率是相符的,在后面第五部分的實證分析中可以得到驗證。由此可知,本文給出的基于因子擴散模型的回收率可以很好的刻畫回收率函數的內生性特征。 信用風險的度量需要計算三個基本核心的參數:違約概率(PD)、違約損失率 (LGD)和違約風險敞口 (EAD)。利用這三個基本參數,就可以得到任何組合債務潛在的信用損失CL,從而進一步的根據信用損失的概率分布獲得信用在險價值(Credit Value at Risk,C-VaR)和預期尾部損失(Expected Tail Loss,ETL)。 首先討論信用損失CL的概率分布。對于具有K份合約的債務組合說,其潛在的信用損失為: (28) 其中PDk、EADk和LGDk分別為債務k的違約概率、違約風險敞口和違約損失率。對于齊次債務組合,有CL=K·PD·EAD·LGD。出于簡化,記EAD=F,LGD=L,故K份合約的齊次債務組合的潛在的信用損失為: CL(Xm)=K·F·PD(Xm)·L(Xm) (29) 下面給出信用損失CL的概率分布。由CL的表達式可知,K,F都是常數,而PD(Xm)和L(Xm)都是市場平均收益率Xm的函數,因此,CL的概率分布fCL(l)dl同市場平均收益率的概率分布fXm(xm)dxm等價的,即 fCL(l)dl?fXm(x)dx (30) 故信用損失CL的概率分布函數為: (31) 根據式子(12)可得: (32) 給定組合信用損失和市場平均收益率之間的函數關系,CL(Xm)=K·F·PD(Xm)·L(Xm),我們可以將市場平均收益率Xm的密度函數轉換為信用損失CL的密度函數: (33) 圖3給出了信用損失CL的理論損失分布的結果和MC結果的對比。 圖3 信用損失的理論分布和MC模擬 從圖3中,我們觀察到信用損失的理論分布和MC模擬的高度的一致性,即使對于極端大的組合損失也是如此。下面利用上面推導的信用風險損失分布來計算兩個重要的信用風險度量指標。 在金融風險管理中,VaR是目前各大金融機構主流的風險度量方法,而且VaR的應用功能已經拓展到了彌補潛在損失所需要的經濟資本、銀行的資本充足率等資本要求的計算中,但是,作為風險管理的主流工具的VaR并不滿足風險度量的一致性要求[32],事實上,雖然VaR滿足單調性、正齊次性和平移不變性,但是它不滿足次可加性,因而無法充分體現資產組合的風險分散效應,這也是本文引入預期尾部損失ETL作為對VaR信用風險度量指標補充的原因。 C-VaR=WCL-ECL (34) (35) 預期尾部損失(Expected Tail Loss,ETL)是Acebi和Tache[33]提出的風險度量方法,它彌補了VaR方法不滿足次可加性的缺陷,是一個具有一致性的風險度量指標。如果X的分布函數FX(x)是連續的,在給定置信水平α下,ETL定義為: (36) 對于信用損失CL來說,預期尾部損失C-ETL為: (37) 下面利用MC技術進行數值計算。考慮一個由500個信用資產構成的同質的債務組合,假設市場價值的初始值為V0=100,零息債券的面值為F=75,到期日為T=1(比如1年)。假設任何兩個資產之間的相關系數為c=0.5,這同股票價格的常見的相關性是一致的。擴散過程的參數設為μ=0.05,σ=0.15,這意味著每年的平均增長率5%和波動率15%。對應的杠桿率F/V0=75%。表1給出基于0.99置信水平的預期信用損失ECL,C-VaR和C-ETL的數值計算的結果。 表1 ECL、C-VaR和ETL的數值模擬和解析結果 注:置信水平α=0.99 從表1可以看出,對于預期信用損失(ECL),信用在險價值(C-VaR)和預期尾部損失(ETL),解析結果同模擬結果高度一致,這說明本文所給出的基于內生性回收率的信用風險的度量模型,能夠很好的對信用風險進行度量。 由于國內還沒有長期完整的債券信用違約數據庫,本文使用了山東大學金融實驗室提供的部分國外的債券信用評級數據。我們對于2000年1月1日到2011年12月31 的債券信用評級數據,根據每一個債務人的違約風險進行排序,從而構建出同質的信用組合。在我們的分析中,我們考慮了組合內不同到期日和相應的回收率的違約概率。 我們測算了2000年1月1日到2010年12月31日的1年期債券的違約概率和回收率。第一段時期從2000年1月1日到2000年12月31日。第二段為2000年2月1日到2001年2月31日,以此類推,最后一段時期為2011年1月1日到2011年12月31日。 由于違約事件是稀有事件,為了盡可能的獲得更多的違約數據,我們考慮了初始評級較低的投機級信用資產組合,這些評級表明相關的信用資產是高風險的。我們統計估算了評級為Caa1,Caa2和Caa3的優先擔保債券的違約概率和回收率,如圖4。 圖4 評級為Caa1,Caa2和Caa3的優先擔保債券的違約概率和回收率 從圖4可以看出,違約概率PD和違約回收率RR二者之間表現出了高度的負相關。實際的數據表明,回收率同違約概率之間是具有內在的聯系的,而不是像大多數文獻所給出的獨立性假設,故回收率是具有內生性的特制的。 下面我們選擇了特定評級的債券組成我們的組合,假設它們在構成組合的相同時刻發行的。理論的預期回收率是根據式子(21)計算的,這實際上是對潛在的隨機過程實現值的一個平均。因此,我們對實際回收率的數據進行平均來描述預期回收率,然后觀察兩者的接近程度。為此,我們將實際的違約率數據等分成30組,然后計算每組的回收率,最后進行平均得到整個資產組合的平均回收率。計算結果畫在圖5中。 圖5 兩年期和四年期違約概率與平均損失及回收率 我們用這些數據來檢驗本文的內生性回收率模型,從圖5 可以發現模型的理論結果同實際的數據高度的一致。內生性回收率模型能夠更好的描述經驗數據。該模型可以作為現存的違約概率模型的一個很好的補充。實際的債務人的資本結構比Merton模型框架內的更加復雜,而且違約通常在到期日之前就發生了。另外,如果我們已經知道違約概率的分布,也可以利用方程(37)來描述組合損失分布。 違約和回收率之間的交互性對大額的信用組合損失具有關鍵的影響。然而在現有的信用風險模型中,違約概率和回收率經常被獨立的模型化。本文基于經典的擴散過程,推導了違約和回收率之間的函數關系。該函數關系是由一個單參數決定的。MC模擬實驗直觀的揭示了違約以及參數如何影響該內生回收率的變化。在內生回收率框架下,本文計算了度量信用風險的兩個重要的指標Credit-VaR和ETF指標。最后利用實際數據檢驗了本文所提出的內生回收率信用風險模型的有效性,結果表明內生回收率信用風險模型可以更好的描述歷史違約率的變化過程。 本文的研究僅僅考慮了信用風險度量中經典的結構模型,對于更多的結構模型也可以利用本文的思路進行拓展。顯然本文所提出的內生性回收率模型可以用在任何其他的違約概率模型中,它可以改進現有的一系列信用風險模型。 此外本文沒有考慮信用風險的定價問題,相信本文的內生性回收率也可以用于信用風險產品(比如,傳統的風險債券和信用衍生品CDS,以及結構化產品CDO分券等)的定價中,這也是作者下一步研究的思路和方向。 [1] Merton R C. On the pricing of corporate debt: The risk structure of interest rates[J]. The Journal of Finance, 1974, 29(2): 449-470. [2] Black F, Cox J C. Valuing corporate securities: Some effects of bond indenture provisions[J]. The Journal of Finance, 1976, 31(2): 351-367. [3] Jokivuolle E, Peura S. A model for estimating recovery rate and collateral haircuts for bank loans [J]. European Financial Management, 2003, 9(3):611-627 [4] Giesecke K. Credit risk modeling and valuation: An introduction[J]. Ssrn Electronic Journal, 2004:1-67. [5] Asvanunt A, Staal A. The corporate default probability model in Barclays Capital POINT Platform (POINT CDP)[M]. Portfolio Modeling, Barclays Capital, 2009. [6] Asvanunt A, Staal A. The POINT Conditional Recovery Rate (CRR) Model[M]. Portfolio Modeling, Barclays Capital, 2009. [7] Jarrow R A, Turnbull S M. Pricing derivatives on financial securities subject to credit risk[J]. The Journal of Finance, 1995, 50(1): 53-85. [8] Jarrow R A, Lando D, Turnbull S M. A Markov model for the term structure of credit risk spreads[J]. Review of Financial Studies, 1997, 10(2): 481-523. [9] Duffie D, Singleton K J. Modeling term structures of defaultable bonds[J]. Review of Financial Studies, 1999, 12(4): 687-720. [10] Houweling P, Vorst A C F. An empirical comparison of default swap pricing models[J]. Journal of labor Economics,2015,33(2):269-296. [11] Frye J. Depressing recoveries[J]. Risk-London-Risk Magazine Limited, 2000, 13(11): 108-111. [12] Pykhtin M. Recovery rates: Unexpected recovery risk[J]. Risk-London-Risk Magazine Limited, 2003, 16(8): 74-79. [13] Andersen L, Sidenius J. Extensions to the Gaussian copula: Random recovery and random factor loadings[J]. Journal of Credit Risk Volume, 2004, 1(1): 29-70. [14] 黃大海. 違約貸款回收率: 基于國外實證研究的分析[J]. 上海金融, 2006, (10): 55-58. [15] 王國棟, 詹原瑞. 信用風險中回收率分布的雙 Beta 模型[J]. 中國管理科學, 2011, 19(6): 10-14. [16] 汪飛星, 姚磊. 聚合信用風險模型的改進和研究[J]. 價值工程, 2013, 32(5): 168-169. [17] 陳暮紫, 陳浩, 馬宇超, 等. 基于廣義 Beta 回歸的不良貸款回收率模型[J]. 數理統計與管理, 2011, 30(5): 810-823. [18] Carty L V, Lieberman D. Defaulted bank loan recoveries[J]. Working Paper,Moody’s Investors Service, 1996. [19] Frye J. Collateral damage detected[J]. Emerging Issues, 2000 (Sep). [20] Bakshi G, Madan D B, Zhang F X. Understanding the role of recovery in default risk models: Empirical comparisons and implied recovery rates[R]. Financial and Economics Board of Governors of the Federal Reserve System (US), 2001. [21] Hu Y T, Perraudin W. The dependence of recovery rates and defaults[R]. Discussion Series,Birbeck College and Bank of Working Paper, England, 2002. [22] Cantor R, Hamilton D T, Ou S. Default and recovery rates of corporate bond issuers[R].Working Paper, Moodys Investors Services, 2002. [23] Carey M, Gordy M. Systematic risk in recoveries on defaulted debt[R].Working Paper Federal Reserve Board,2003. [24] Altman E I,Brady B, Restiand A, et al. The link between default and recovery rates: Theory, empirical evidence and implications [J]. Journal of Business,2005,(78):2203-2228. [25] Hamilton D T.Default and recovery rates of corporate bond issuers: 2000 [R].Working Paper,Moody.s Investors Service,2001. [26] Hu Yen-Ting, Perraudin W.The dependence of recovery rate and defaults[R]. Working Paper,Birbeck College and Bank of England,2002. [27] Hull J C, White A D.Valuation of a CDO and an nth to default CDS without monte carlo simulation[J].The Journal of Derivative,2004,12(2): 8-23. [28] Das S R, Hanouna P. Implied recovery[J]. Journal of Economic Dynamics and Control, 2009, 33(11): 1837-1857. [29] Guo Xin, Jarrow R A, Zeng Yan. Modeling the recovery rate in a reduced form model[J]. Mathematical Finance, 2009, 19(1): 73-97. [30] Chava S, Stefanescu C, Turnbull S. Modeling the loss distribution[J]. Management Science, 2011, 57(7): 1267-1287. [31] 陸懋祖. 高等時間序列經濟計量學[M]. 上海:上海人民出版社, 1999. [32] 孫立娟,風險定量分析[M].北京:北京大學出版社,2011. [33] Acerbi C, Tasche D. On the coherence of expected shortfall[J]. Journal of Banking & Finance, 2002, 26(7): 1487-1503. Endogenous Recovery Rate and Credit Risk Measurement WU Jian-hua1, WANG Xin-jun2, ZHANG Ying1 (1.School of Mathematical Sciences, University of Jinan, Jinan 250022,China;2.School of Economics, Shandong University, Jinan 250100,China) In credit risk models, exogenous recovery rate may neglect the impact on the tail of the loss distribution, and the exogenous specify of the recovery rate leads to the possible model risk. This paper incorporates the factor diffusion process into the structure model of default, derives the inherent relation between the recovery rate and the default probability and analyzes the dependence of expected recovery rate on the expected default probability by using the MC technology. The result shows there are strong negative correlation between expected recovery rates and default probability. Furthermore, the volatility of the asset value has positive compact on the correlation. In the framework of the endogenous recovery rate, the probability distribution of the credit loss is derved, and two index, Credit VaR and ETF, which is the measurement of the credit risk are computed. Finally, the performance of the endogenous recovery rate is tested-based on credit risk model using the market data,which shows that the model can well-character the evolution of the history default probability and recovery rates. endogenous recovery rate; factor diffusion process; credit risk measurement; numerical simulation; empirical analysis 1003-207(2016)01-0001-10 10.16381/j.cnki.issn1003-207x.2016.01.001 2014-02-19; 2014-07-17 教育部人文社科規劃基金資助項目(13YJAZH091); 國家社會科學基金資助項目(12BTJ015); 濟南大學社科基金資助項目(15Y1329);濟南大學優秀人才科研基金資助項目(1008359,1008645) 簡介:吳建華(1975-),男(漢族),山東博興人,濟南大學數學科學學院,講師,校聘A4崗,研究方向:精算與風險控制、金融風險量化與管理,E-mail:wu88172968@163.com. F832 A3 基于因子擴散模型的內生回收率
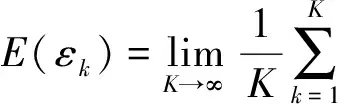
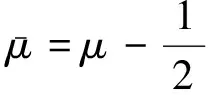
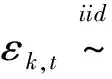
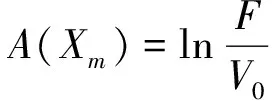
4 基于內生回收率的信用風險度量
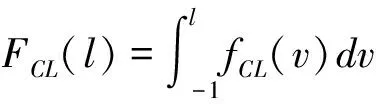
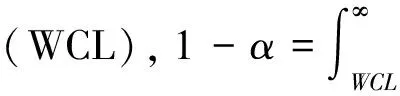
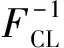

5 內生性回收率的實證檢驗
6 結語

