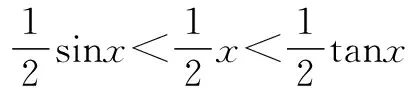例析構造法在數學中的應用

劉宗亮●

廣東省河源市東源縣東源中學(517500)

?

例析構造法在數學中的應用

劉宗亮●

廣東省河源市東源縣東源中學(517500)

本文筆者先闡述了構造法的定義與特點，并且結合日常的解題教學對常用的構造法進行了整理與歸納。值得大家參考與學習.

例析；構造法；數學；應用

構造法是解決數學問題的一種重要方法，用構造法解題有著你意想不到的功效，問題很快便可解決.構造法中構造的方式很多，它可以構造函數、方程、向量、數列、幾何圖形甚至其它構造，就會促使學生要熟悉幾何、代數、三角等基本知識技能并多方設法加以綜合利用.因此，在解題教學時，若能啟發學生從多角度，多渠道進行廣泛的聯想則能得到許多構思巧妙，新穎獨特，簡捷有效的解題方法而且還能加強學生對知識的理解，培養思維的靈活性，提高學生分析問題的創新能力.

下面筆者結合平常的解題教學經驗，對在數學應用中常用的構造法進行如下歸納與例析：

一、構造函數

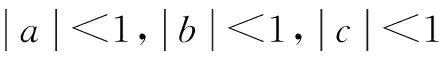
ab+bc+ca>0．

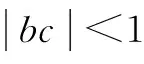
若b+c≠0,則f(a)是一次函數且為單調函數，

f(a)的值在f(1),f(-1)之間，而f(1)=(b+c)+(bc+1)=(1+b)(1+c)>0…①

f(-1)=-(b+c)+(bc+1)

=(1-b)(1-c)>0…②

由一次函數的性質及①、②兩式知：

f(a)>0，

即ab+bc+ca>0．

二、構造方程

例2 設實數a,b,c滿足a2-bc-8a+7=0且b2+c2+bc-6a+6=0，求實數a的取值范圍.

解析 由b2+c2+bc-6a+6=0

變形為

(b+c)2=bc+6a-6=a2-8a+7+6a-6=a2-2a+1=(a-1)2，

得到b+c=±(a-1),bc=a2-8a+7．

從而可構造方程

x2±(a-1)x+a2-8a+7=0

三、構造向量

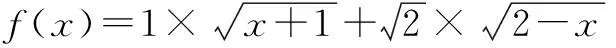
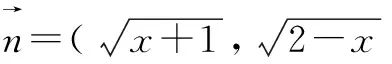
四、構造幾何圖形

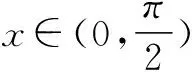
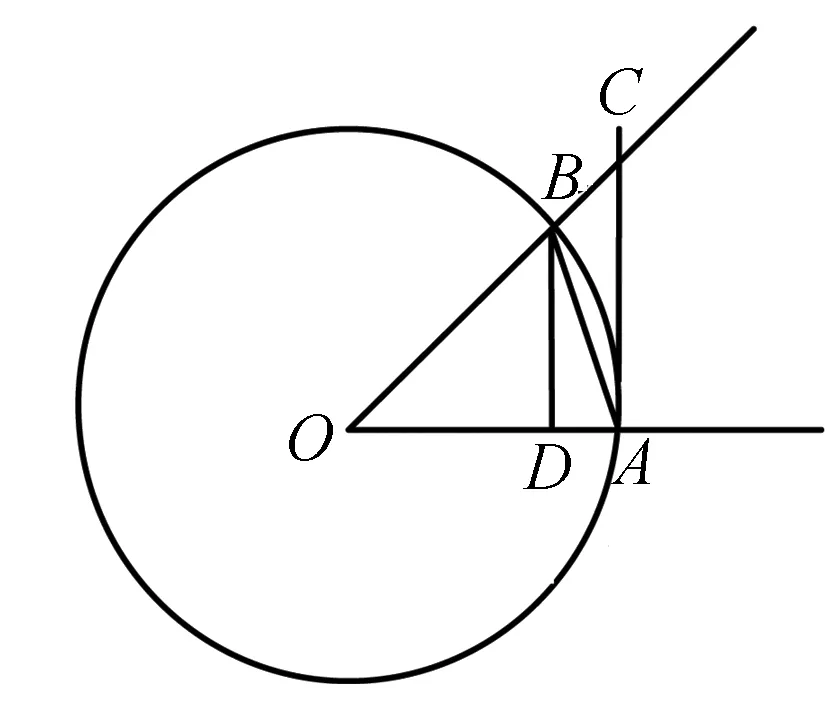
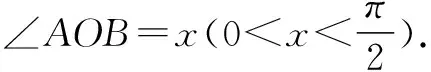
AC切⊙O于A，BD⊥OA于D，

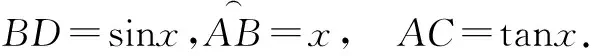
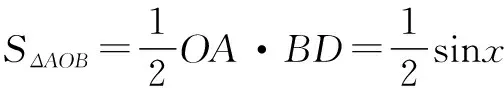
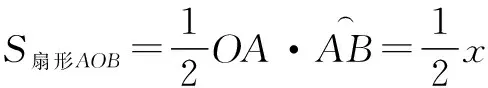
∵SΔAOB

∴sinx

[1]胡上生．例談不等式證明中常見構造法[J]．福建中學數學，2015(2)．

G632

B

1008-0333(2016)28-0044-01