例析以立體幾何為載體的空間最值問題的求解策略

侯 軍● 苗 會●

云南省紅河州石屏高級中學(xué) (662200) 中央民族大學(xué)附中海南陵水分校(572400)

?

例析以立體幾何為載體的空間最值問題的求解策略

侯 軍● 苗 會●

云南省紅河州石屏高級中學(xué) (662200) 中央民族大學(xué)附中海南陵水分校(572400)

在近幾年的高考題和高三模擬題中經(jīng)常出現(xiàn)一類以立體圖形為載體的空間最值問題,這類問題對學(xué)生的識圖、用圖能力以及對立體圖形的空間想象力要求較高，有助于考查學(xué)生的探究能力和思維的創(chuàng)造性.在教學(xué)中，我們發(fā)現(xiàn)同學(xué)們面對此類問題時普遍不知如何下手，故本文以此為背景，介紹幾種求解立體幾何最值問題的常用策略.

策略一 直觀感知，考慮特殊位置

例1 (2016浙江卷理科第14題)如圖1，在△ABC中，AB=BC=2,∠ABC=120°.若平面ABC外的點P和線段AC上的點D，滿足PD=DA,PB=BA,則四面體PBCD的體積的最大值是____.

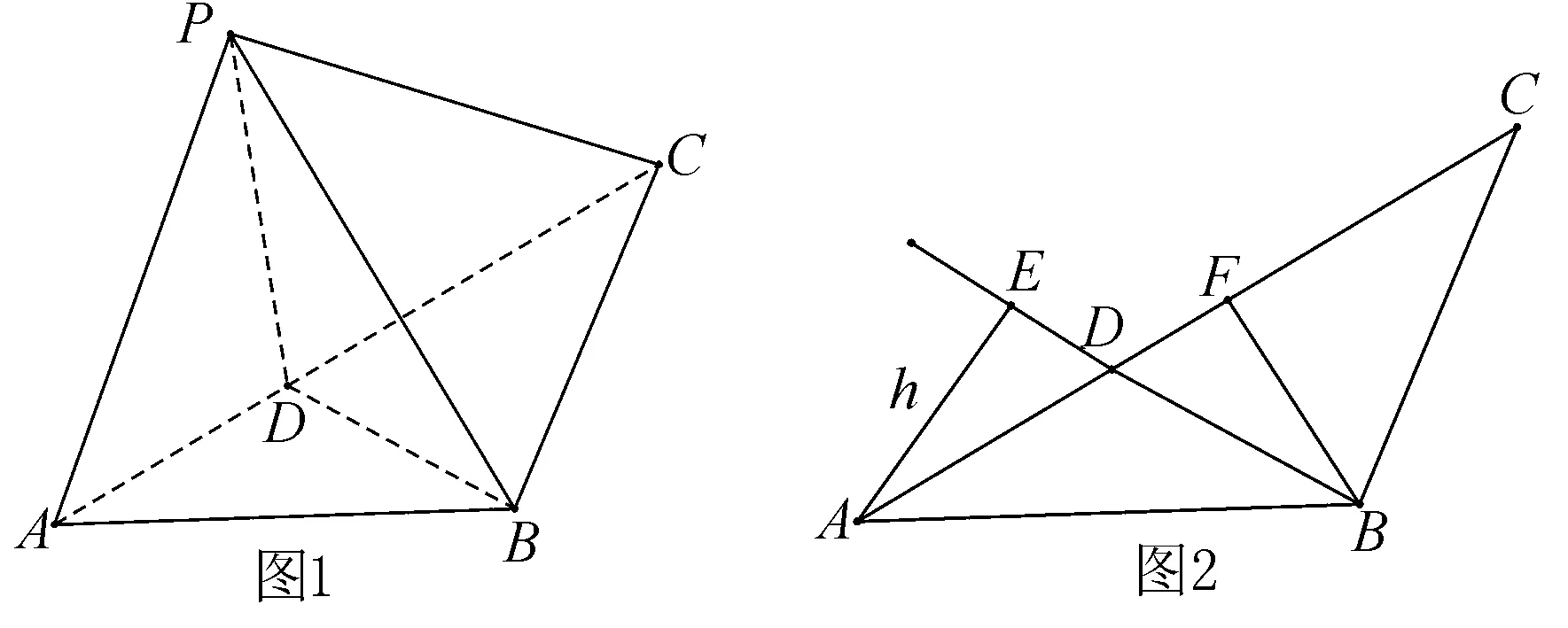
分析 因為PD=DA,PB=BA,則本題可轉(zhuǎn)化為△ABC沿著BD翻轉(zhuǎn)過程中,何時三棱錐P-BCD的體積取得最大值. 通過幾何直觀感知可知，當平面PBD⊥平面BCD時，體積取得最大值.

點評 本題關(guān)鍵在于對PD=DA,PB=BA這一條件的巧妙解讀，使問題轉(zhuǎn)化為翻轉(zhuǎn)問題這一我們熟悉的題型.

策略二 將立體圖形問題轉(zhuǎn)譯成不等式問題求最值

例2 某幾何體的三視圖如圖3所示,當xy最大時,該幾何體的體積為____.

分析 由三視圖為三個三角形可知幾何體為三棱錐，考慮到“正、側(cè)、俯視圖長對正，正、側(cè)視圖高平齊，俯、側(cè)視圖寬相等”的特點可以找出三棱錐的關(guān)鍵數(shù)據(jù)，進而利用均值不等式構(gòu)造不等關(guān)系求最值.

解 該幾何體的直觀圖如圖4所示：

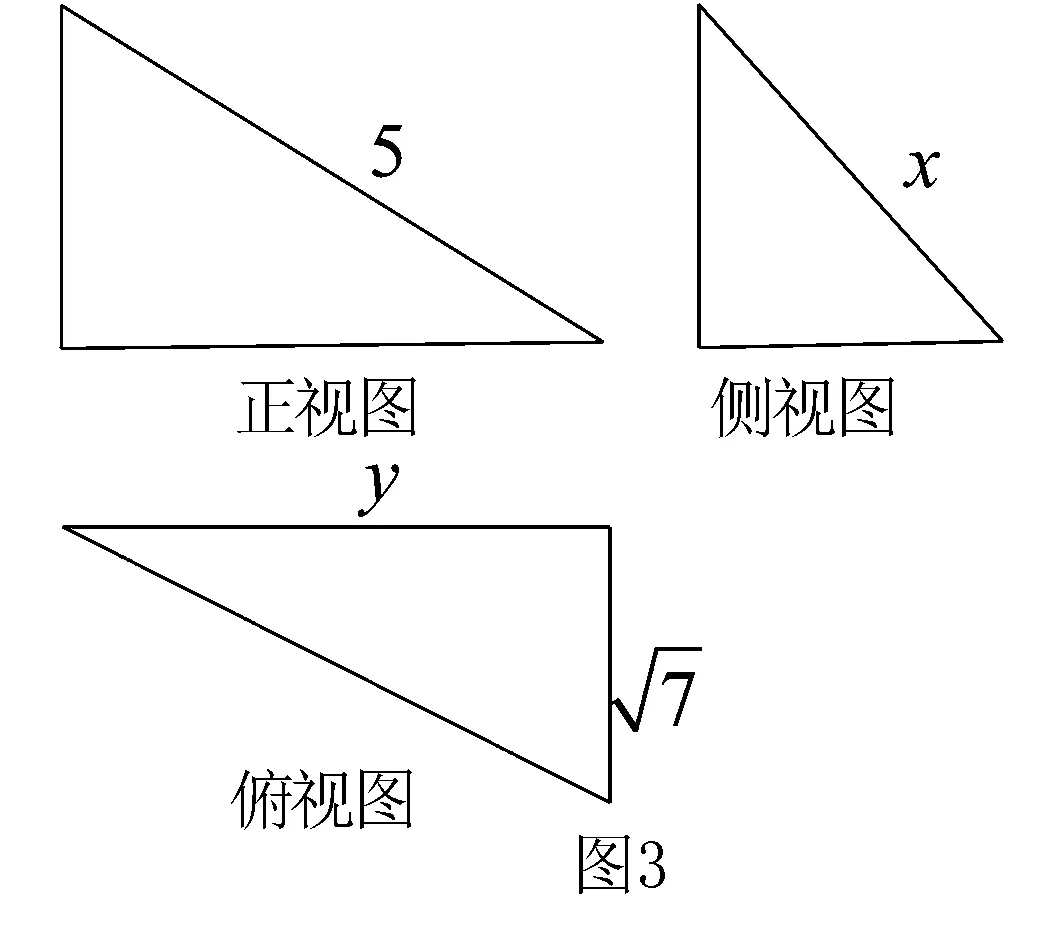
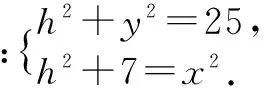
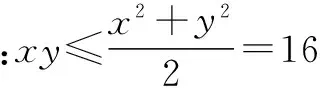
點評 同學(xué)們不難畫出該三視圖所對應(yīng)的直觀圖，本題的“卡點”在于很多同學(xué)不知道如何合理地構(gòu)造不等關(guān)系，事實上，在立體幾何中搭建不等關(guān)系時，a2+b2≥2ab這一結(jié)構(gòu)的基本不等式使用頻率更高，這主要源于它與勾股定理a2+b2=c2這一代數(shù)結(jié)構(gòu)的知識聯(lián)結(jié).

策略三 將立體圖形問題轉(zhuǎn)譯成函數(shù)問題求最值

例3 已知正六棱柱的12個頂點都在一個半徑為3的球面上，當正六棱柱的體積最大時，其高為 ( ).

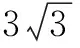
分析 正六邊形可以劃分為6個正三角形，這也是求正六邊形底面面積的常用思路.考慮到正六棱柱的對稱性，故其外接球的球心必為上下底面中心連線的中點，不妨以高為自變量建立關(guān)于體積的函數(shù)，將問題轉(zhuǎn)化為求函數(shù)的最大值問題.

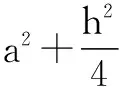
點評 以立體幾何為依托建立函數(shù)關(guān)系時，出現(xiàn)了我們熟悉的三次函數(shù)，對于絕大多數(shù)同學(xué)而言，通過求導(dǎo)的方法來求函數(shù)的最大值自然變得親切、可愛，易于聯(lián)想.

策略四 將立體幾何問題轉(zhuǎn)譯成解析幾何問題求最值

例4 (2012年上海卷理科第14題)如圖6所示,AD與BC是四面體ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a,c為常數(shù),則四面體ABCD的體積的最大值是____．

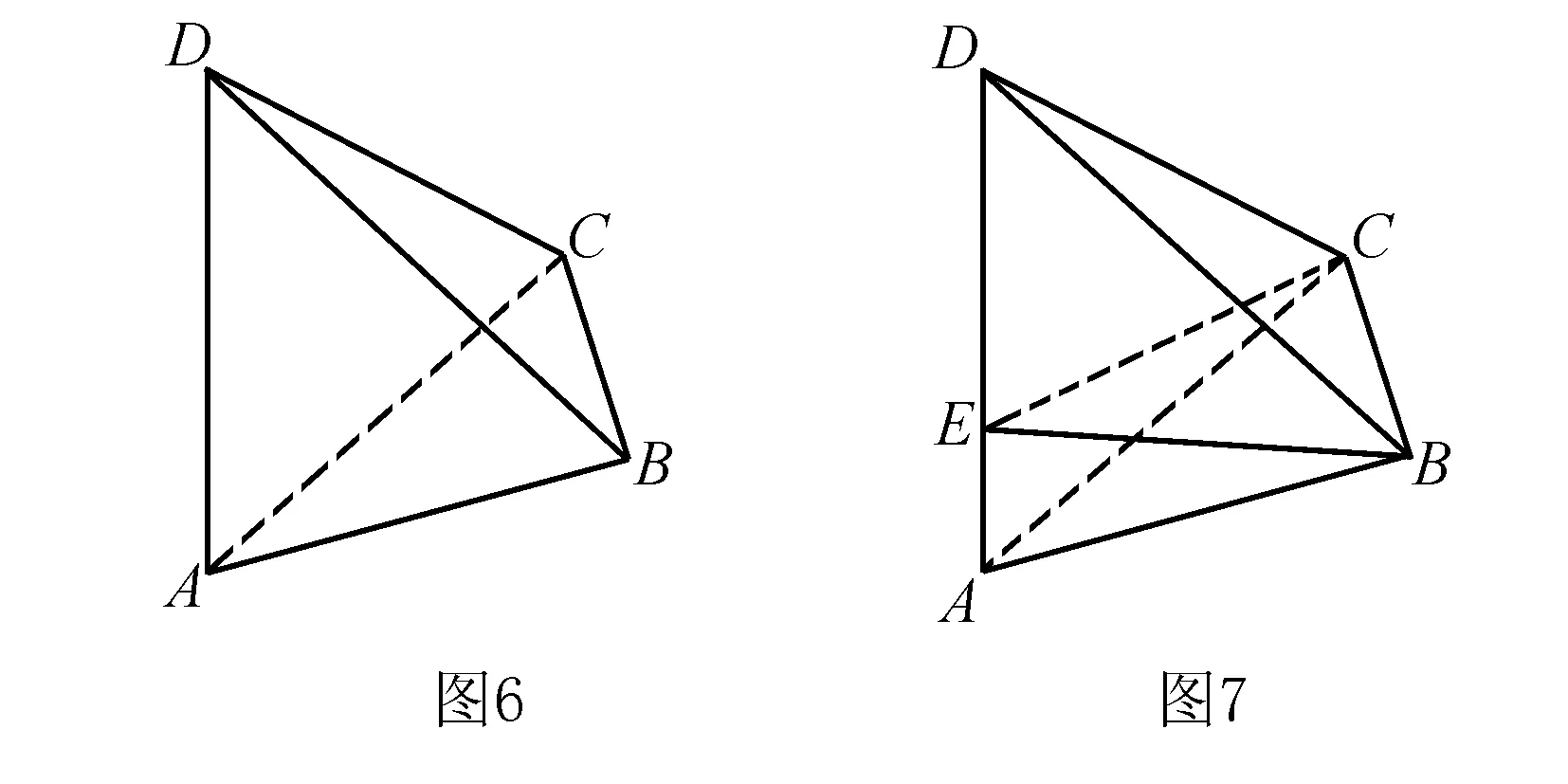
分析 “AD與BC是四面體ABCD中互相垂直的棱”是本題的重要切入點，不妨過點B作該四面體的一個垂面BCE，將四面體的體積進行“切割”.

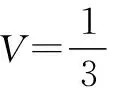
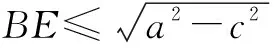
點評 本題初看毫無頭緒，將四面體“切割”后，運用橢圓的定義將立體幾何問題巧妙的轉(zhuǎn)化為解析幾何問題處理，讓問題變得柳暗花明，可見同學(xué)們在解題時要充分聯(lián)想，敢于嘗試.

策略五 將立體圖形問題轉(zhuǎn)譯成平面圖形問題求最值

例6 如圖8所示，已知正四面體ABCD的棱長為1,M為BC的中點,P在線段DM上,則(AP+BP)2的最小值為____.

分析 只需求AP+BP這一線段和的最小值，故我們不妨將立體圖形展開為平面圖形再利用平面內(nèi)兩點間距離最短這一性質(zhì)進行求解.

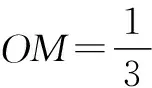
點評 將立體圖形沿某條棱展開成平面圖形是求此類線段和最值問題的通性通法，其特點是通過展開平面使兩條線段在同一個平面內(nèi).本題不僅運用了這一方法，更在此基礎(chǔ)上應(yīng)用余弦定理，考查了學(xué)生對已學(xué)知識的有效遷移能力.

G632

B

1008-0333(2016)28-0009-02