在變化中找不變
——淺談動態幾何中利用面積的不變量關系解題

浙江省慈溪市三北初級中學(315331)

黃群暉●

?

在變化中找不變
——淺談動態幾何中利用面積的不變量關系解題

浙江省慈溪市三北初級中學(315331)

黃群暉●

動態幾何問題，體現了近代數學運動變化的思想，是近幾年數學中考命題的重點，解這類題目的一般方法是抓住變化中的“不變量”，以不變應萬變.本文以利用面積的等量關系如何解題為例，淺談動態幾何中利用面積的不變量關系解法及啟示.

不變量；幾何動態；面積；解法啟示

動態幾何題，包含了一些“動態”的點、線段、直線等元素，給靜態的平面幾何題賦予了活力，使題意更新穎.同時“動態”的存在也使平面幾何題更趨靈活，加強了對學生想像能力的考查.動態幾何問題中往往有很多變量，還有很多圖象、數據按一定規則進行變換和操作，這些無疑增加了問題的復雜性，給問題的解決增加了難度.但在這些復雜變化的背后總是隱藏著一些沒有變化的東西，那就是不變量，抓住不變量就成了解決問題的關鍵.

為了大家可以清晰地了解不變量在處理幾何問題的便捷，在這里我簡單的舉兩道例題來說明.

一、利用面積不等量關系的解法

例1 (2013·寧波)7張如圖1的長為a，寬為b(a>b)的小長方形紙片，按圖2的方式不重疊地放在矩形ABCD內，未被覆蓋的部分(兩個矩形)用陰影表示．設左上角與右下角的陰影部分的面積的差為S，當BC的長度變化時，按照同樣的放置方式，S始終保持不變，則a，b滿足( ).

A．a=2.5bB．a=3bC．a=3.5 bD．a=4b

一般情況下的解法是：

解 左上角陰影部分的長為AE，寬為AF=3b，右下角陰影部分的長為PC，寬為a，

∵AD=BC，即AE+ED=AE+a，BC=BP+PC=4b+PC，

∴AE+a=4b+PC，即AE-PC=4b-a，

∴陰影部分面積之差S=AE·AF-PC·CG=3bAE-aPC=3b(PC+4b-a)-aPC=(3b-a)PC+12b2-3ab，則3b-a=0，即a=3b．故選B

用不變量來解題：

解 既然BC是變化的，當點P與點C重合開始，然后BC向右伸展，

設向右伸展長度為X，左上陰影增加的是3bX，右下陰影增加的是aX，因為S不變，

∴增加的面積相等，∴3bX=aX，∴a=3b．

故選B.

從上面解題過程可以得出，在動態幾何教學中我們如果讓學生學會用不變量來解題，學生非常容易找到等量關系，列出合適的、簡便的方程，解題速度也大大加快.特別如上題作為2013年寧波數學中考的最后一題選擇題，許多學生在印象中認為這題一定很難很復雜，容易產生心理上的恐懼.因此，用一般方法來解題就存在兩大缺陷，第一比較費時容易使學生產生緊張心理，第二容易出現計算錯誤.若此題用不變量“增加的面積相等”來解此題，在中考中既安定了心神，又為后面解題引得了時間.因此，在平時教學中，我覺得讓學生在動態幾何中找到不變量，利用不變量來解題，是非常好的一條捷徑.

二、利用面積的等量關系解題的啟示

1.仔細審題，有的放矢

認真讀題——俗話說得好：“讀書百遍，其義自見.”對于幾何語言的理解能力尚處在培養期的七年級學生而言，培養他們認真讀題特別重要.它不僅是學生正確理解題意的基礎，還是學生正確解決問題的根本保證.因此在幾何數量關系的揭示中，涉及很多名詞術語，語言敘述有順有逆，數據顯示有明顯、有隱含，題目結構變化多樣，因此，學生對題意的理解并非是容易的事.這就要求我們老師在訓練學生讀題時，要讓學生學會抓關鍵詞.

2.理解題目，理清關系.

(1)找到運動中變化的點、線、量.如上例中，我們通過審題發現，BC的長度是在不斷變化的，隨著此變化，左上角與右下角的陰影也是在不斷變化的.

(2)找出在運動中不變的點、線、量.如上例中，小長方形的長和寬不變，左上角與右下角的陰影部分的面積的差S始終保持不變.

3.列出方程，解決問題.

在上題中，我們利用面積差S不變，那么在變化過程中，左上角和右下角增加的面積相等，以而列出“左上角增加的面積=右下角增加的面積”.

4.鞏固訓練，養成習慣.

葉圣陶先生說：“習慣是從實踐中培養出來的，知道一點做一點，知道幾點做幾點.積累起來，各方面都養成習慣，而且都是好習慣，就差不多了.”在數學問題中，有許多解是符合方程的，但卻不符合題意或者不符合實際生活需要，所以我們要養成驗算的習慣，這樣既可避免由于計算錯誤造成的失分，又可保證自己解題的正確性.我認為，利用面積不變量解幾何動態問題還是需要一定的練習來鞏固的.因此我出了下面一題來使同學們加強練習.

例2 如圖,點E是邊長為2的正方形ABCD的邊AB的中點,點F是BC延長線的點，EF交CD與G，若四邊形AEGD的面積=△CGF的面積=S，并且S△CGF÷S△BEF=(CF÷BF)2，則S=____.

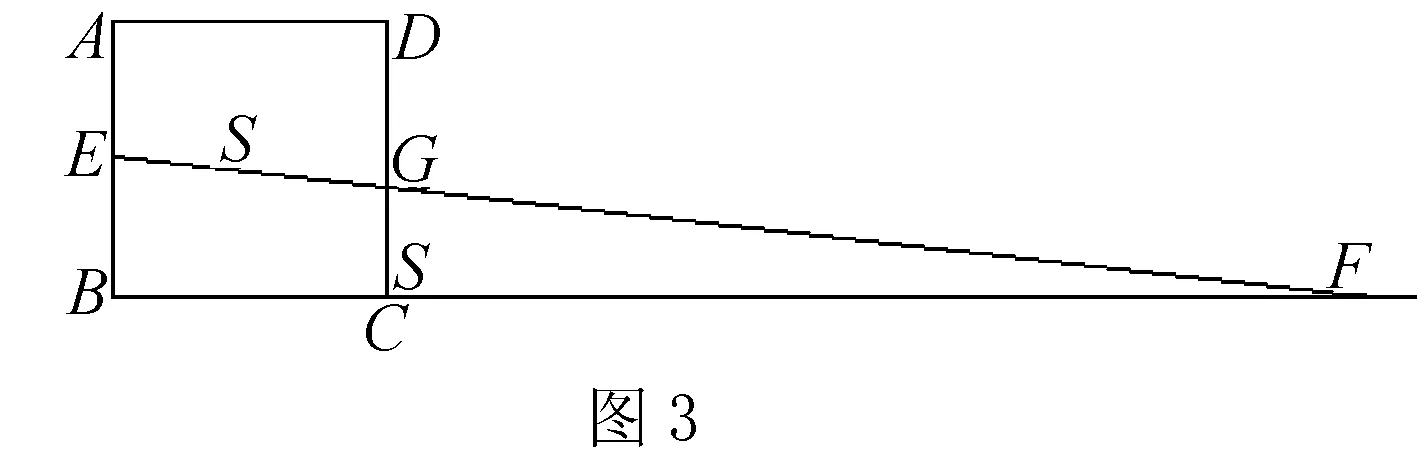
一般情況下的解法是：

解 ∵四邊形AEGD的面積=△CGF的面積=S，S△CGF÷S△BEF=(CF÷BF)2.

??

用不變量來解題：

解 ∵四邊形AEGD的面積=△CGF的面積=S，

∴△BEF的面積=正方形ABCD的面積

∴BE×BF÷2=4 ∴1×(2+CF)÷2=4

∴CF=6 ∴S=(CF÷BF)2×4=2.25

此題對于七年級學生來講是不可能用上述的一般方法來解的，因為相似和兩個未知數方程對他們來說都是沒有學過的.即使九年級學生解起來也比較困難，比較花時間.但七年級的學生們用四邊形AEGD的面積=△CGF的面積=S，得到△BEF的面積=正方形ABCD的面積，利用不變量來解此題，一下就輕松解決了.

通過這兩道例題我們可以看到，做幾何動態類的題目.往往用題目中的動點、動線是很難解決的，可是利用動態中的不變量來解題就輕松、便捷了許多.通過本文的講解以及例題的演示，我希望這篇文章能夠為大家帶來益處.不過，由于個人的數學知識有限，可能對于動態幾何題不變量在解題中的技巧歸納不夠深入，希望在以后的學習和工作中繼續完善.

(1)張保利.動態型數學問題的思考路徑，《中學生數理化》，2004年16期

(2)《怎樣解題》美國,數學家和數學教育家G波利亞

G

B