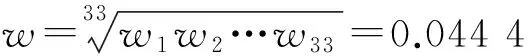城市生態系統網絡穩定性的理論計算與分析
馬寨璞,張凱利,李帥強,王慧欣,王孟孟
(1.河北大學 生命科學學院,河北 保定 071002;2.鄭州宇通客車股份有限公司 海外產品事業部,河南 鄭州 450061)
?
城市生態系統網絡穩定性的理論計算與分析
馬寨璞1,張凱利1,李帥強2,王慧欣1,王孟孟1
(1.河北大學 生命科學學院,河北 保定 071002;2.鄭州宇通客車股份有限公司 海外產品事業部,河南 鄭州 450061)
為了計算城市生態系統網絡的穩定性,分析了城市生態系統網絡的構成特點,確定了以網絡基元為基本分析單位的網絡穩定性計算思路,定義了標準網絡基元及網絡基元與網絡整體穩定性的計算方法.虛擬生態系統網絡樣例計算證明該方法可行,并具體計算了實際三線城市生態系統網絡的穩定性,計算結果合理.
城市生態系統;網絡基元;網絡穩定性
生態系統穩定性是指生態系統受到干擾時抵抗偏離初始狀態的能力,或者受到干擾后返回初始狀態的能力[1],穩定性也是生態系統的重要特征之一.城市是人類生存和生產活動的重要核心場所,城市環境與人類活動共同構成的城市生態系統,是生態系統的重要組成部分,其穩定性直接關系到整個社會的發展,對城市可持續發展具有重要意義[2].
目前,對生態系統穩定性的研究,主要側重于理論研究[2],穩定性個例研究主要集中在土壤[3]、濕地[4-5]、農田[6-7]、水域和森林[8-9]等自然生態系統,對于具有復雜性的城市生態系統穩定性的研究則比較少,到目前為止,還沒有建立起科學、完整的評估方法和體系[10].
城市生態系統由許多組分構成,各個組分又由不同的指標加以評價,如果將每一個選取的指標看作一個節點,那么城市生態系統就可表達成由這些節點構成的城市生態系統網絡[11].城市生態系統的穩定性,外在表現就是城市的正常運行與可持續發展,體現在城市生態系統網絡上,則城市生態系統網絡應具有一定的穩定性.基于此,本文首先分析了城市生態系統網絡的基本特點,探討了計算城市生態網絡穩定性的方法,并以三線城市生態網絡為例,計算了其生態系統的穩定性狀況.
1 確定網絡基元
網絡的類別不同,則構成網絡的基本單元也各不相同,Alon等將基因調控網絡中出現頻率較高的連接子圖定義為網絡基元[12],網絡基元也是分析網絡本質特征的出發點,因此,城市生態系統網絡基元的確定也就至關重要.
在城市生態系統中,自然、社會、經濟三大子系統又由不同的指標組成,系統網絡的構建,則基于對科學選定指標的連接,圖1是安秋丹等[11]構建的三線城市生態系統網絡.城市生態系統網絡是一個虛擬的具有相關關系的網絡,若將其看作是二維網絡,則構成網絡的邊線量值是連接節點的相關系數值(絕對值).從相關的角度來看,構成一個網,至少包含相互關聯的3個節點,因此,對于二維城市生態網絡,相關三角形可看作其網絡基元.若將城市生態網絡看作是三維立體網絡,則構成空間網絡結構的基本單元至少應包含4個節點,以邊線連接4個節點,則連接而成的(廣義)錐體可看作是該網絡的網絡基元.
一個典型的平面二維生態網絡,可由圖2虛構樣例的城市生態網絡圖表達,圖2中,節點之間具有連接說明兩點之間具有相關性,連接邊的長度則對應著兩節點之間的相關系數值(絕對值).能夠連接成三角形的3個節點,比如連接節點5、7、8的三角形,則可以看作是最簡單的網絡(低于3點的連接不成為網絡),也是穩定性分析的網絡基元.

圖1 三線城市生態系統網絡Fig.1 Urban ecology network of the third-tier cities
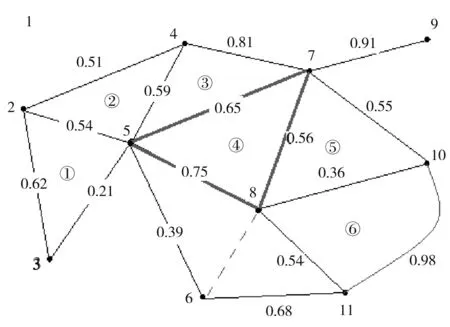
圖2 虛構的城市生態系統網絡Fig.2 Urban ecology network of virtual city
2 網絡基元穩定性分析
城市生態系統網絡可看作二維或三維的網絡,當城市生態系統網絡被看作由相關三角形組成的二維網絡時,則生態系統網絡整體穩定性取決于2個方面,一是基元自身的穩定性,二是基元之間由于相互作用而涌現出的整體穩定性.要準確計算網絡整體穩定性,就有必要先計算出每個基元的穩定性.在圖2中,取出由節點5、7、8連接而成的相關三角形,該網絡基元的穩定性如何計算就成為解決問題的焦點.
2.1 穩定性計算的幾種思考
要計算一個三角形的穩定性,將三角形的穩定性具體表達出來,可以有不同的方法.通常說的三角形具有穩定性,這種穩定性更多地是講結構不變性,是和構成三角形的三邊材料有關的屬性;另一種提法是根據三角形重心位置來衡量穩定性,三角形形狀改變后,其重心位置也發生改變,其穩定性也相應改變,但是需要滿足重心原理,幾何重心在底面的投影可落在支撐面內,該方法適合三維空間中三角錐穩定性的計算;此外,三角形的穩定性與三角形的形狀有關,因此,筆者認為,三角形的穩定性和構成三角形的3個頂點之間的相互位置有關.基于此,使用頂點到對邊的距離(即高線)來表達三角形的穩定性,即可用3條高線之和來表達穩定性.但是,這仍然存在一個問題,即當3條高線和相等時,2個三角形的穩定性也不完全相同.本文考慮利用高和面積,并最終轉化為相關三角形的面積比來確定網絡基元的穩定性,再由網絡基元穩定性計算網絡整體穩定性.
2.2 網絡基元面積比的確定
2.2.1 標準網絡基元的選定
相關三角形的3條邊長代表了節點間的相關系數,根據相關系數的性質,可知|r|≤1,相關系數絕對值越接近于1,則2個節點之間的相關性就越大,由此可見,最穩定的相關三角形是3條邊長都為1的等邊三角形.相關三角形的每條邊長都在0~1內變動,所以由節點構成的這些相關三角形只能在這個最穩定三角形內部進行變化,即所有相關三角形面積都小于這個最穩定的相關三角形的面積.如圖3示意,以△ABC為上述等邊三角形,則為普通相關三角形.節點間相關系數的改變將導致相關三角形穩定性的改變,將穩定性以面積和高表達,設S是相關三角形面積,C是相關三角形周長,a、b、c是相關三角形邊長,h是底邊上的高,θ2、θ3是底邊與兩邊的夾角,各參數如圖3所示,則有
(1)
根據式(1)和正弦定理可得
(2)
相關系數極少都等于1,考慮一邊具有最大相關性的情況,即當a=1時,
(3)
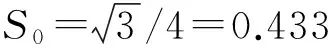
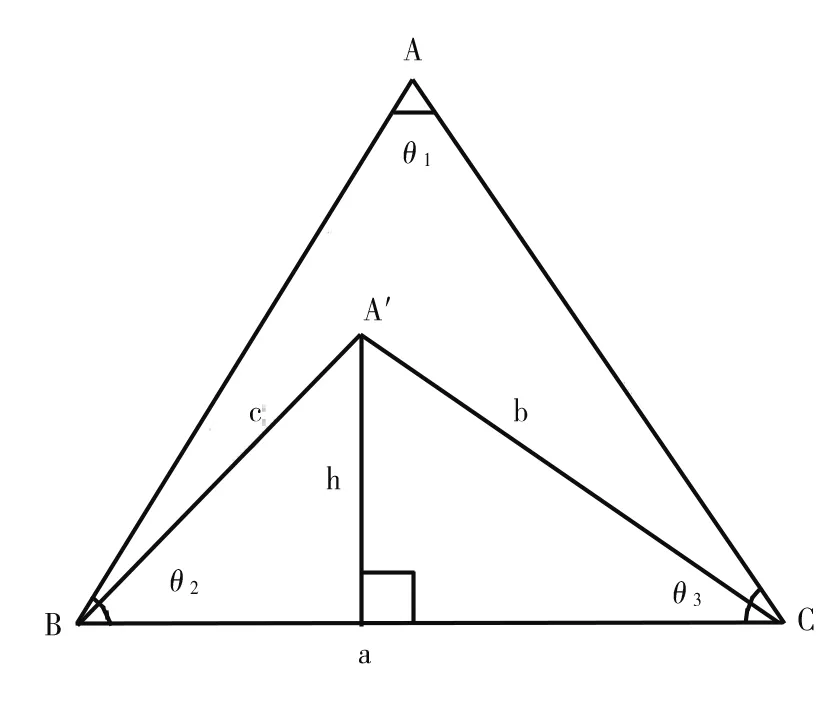
圖3 普通三角形Fig.3 Ordinary triangle
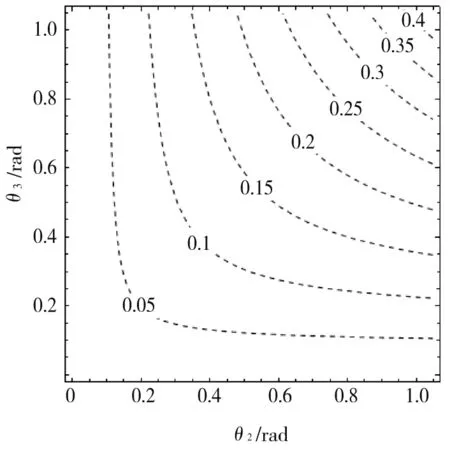
圖4 穩定性隨角度變化Fig.4 Change of stability along with angle
2.2.2 面積比的計算方法
已知相關三角形的邊長a、b、c,根據式(4)即可求出面積S,為了更加準確地判定網絡基元穩定性,將網絡基元的面積S與標準網絡基元的面積比來表示網絡基元穩定性,如式(5).
(4)
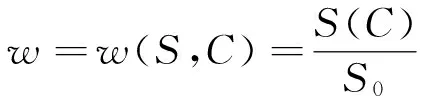
(5)
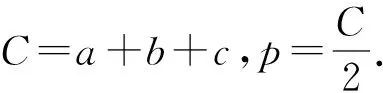
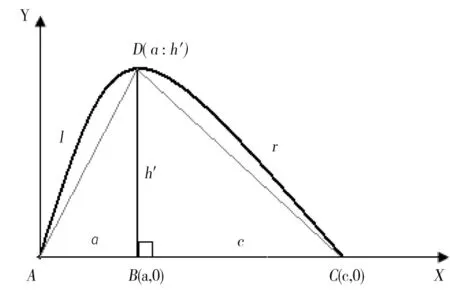
圖5 曲線三角形Fig.5 Curved triangle
2.2.3 異常三角形的處理
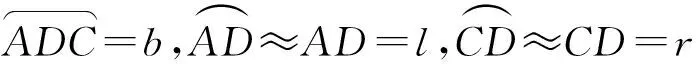
設過A、D、C三點的拋物線為
y=f(x)=αx2+βx+γ.
(6)
根據多項式擬合,則由三點坐標表達的擬合方程組如下:
(7)
求解(7),得到
(8)
代入(6),得到,
(9)
據圖5可知,
r+l=b,
(10)
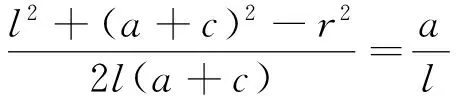
(11)
由方程(10)(11)可得,
(12)
則曲線△ABC的面積表達式為(定積分得出)
(13)
2.2.4 四邊形的處理
城市生態網絡中,各節點之間不一定都有關聯,因此,有可能出現圖2中像節點5、6、8、11,4個節點連接情況,4個節點只能連接成一個四邊形,但由于6~8與5~11之間沒有關聯,無法形成網絡基元.對于這種情況,在計算穩定性時,因為使用面積比來表達穩定性,當這4個節點圍成的面積不計入穩定性計算時,顯然不合理,要將該四邊形計入面積比,則必須確定節點6~8或者5~11之間的連線.
在城市生態網絡中,類似四節點圍成區域的情況,其針對的理論模型如圖6所示,在圖6中,設有1、2、3、4,4個節點連接而成四邊形,1~4與2~3之間沒有連接,設連接兩點的連線為l1,4、l2,3,則根據邊長的含義,應該取l2,3=0,l1,4=0,但這樣處理,會造成2和3點的重疊或1和4點的重疊(距離為0的結果),顯然不符合已存在的其他兩邊的約束.筆者認為,2個節點之間沒有關聯,即本質上l2,3=0或l1,4=0,彌補連接線的主要目的是為了計算面積比,因此,在彌補時,一個最優的選擇是:在滿足構成相關三角形的前提下,讓l1,4、l2,3盡可能地取最小滿足值.這樣,得到如下的約束:
極小值約束
min{l1,2+l1,3>l2,3,l2,4+l3,4>l2,3},min{l1,2+l2,4>l1,4,l1,3+l3,4>l1,4}.
(14)
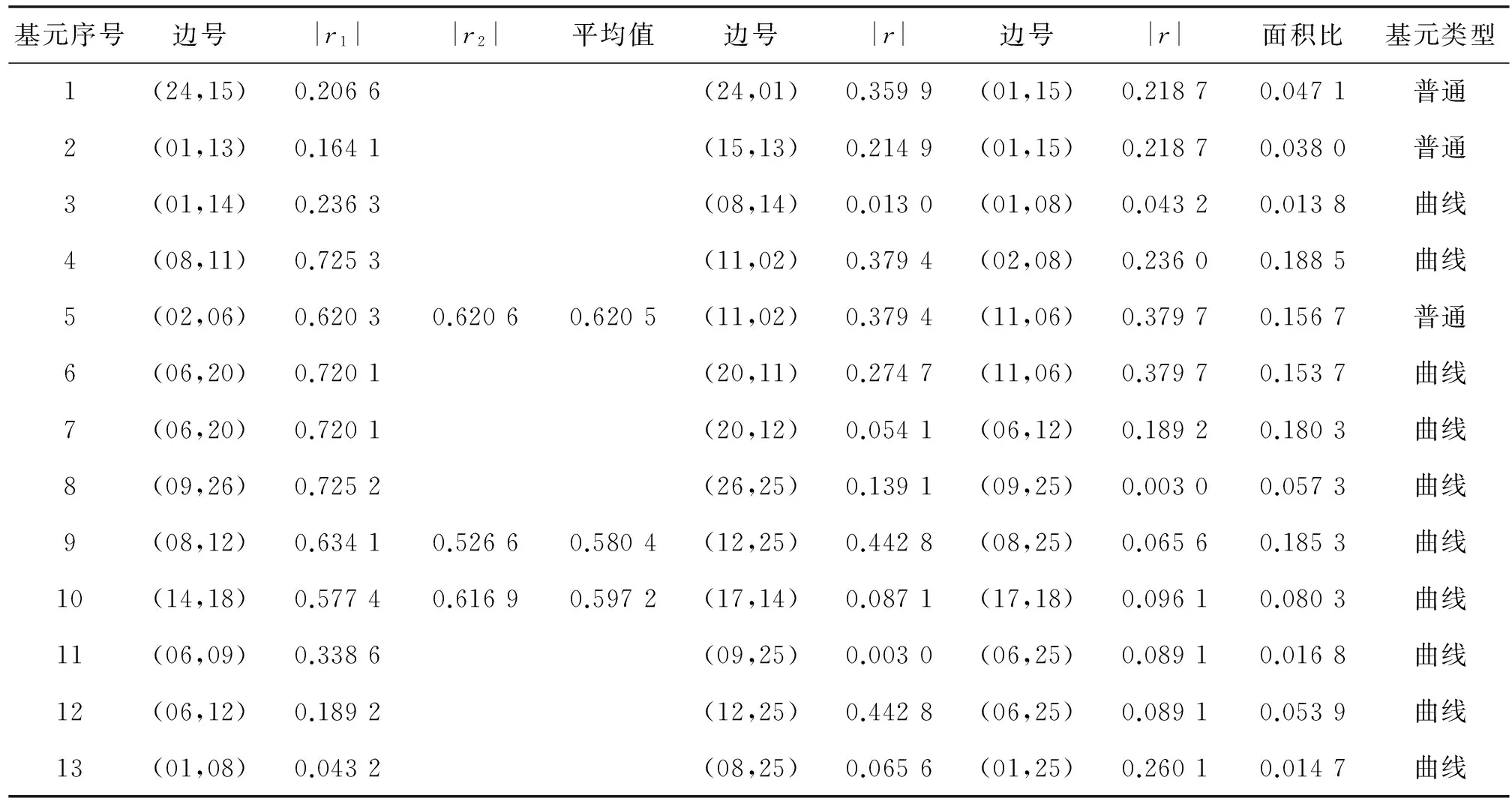
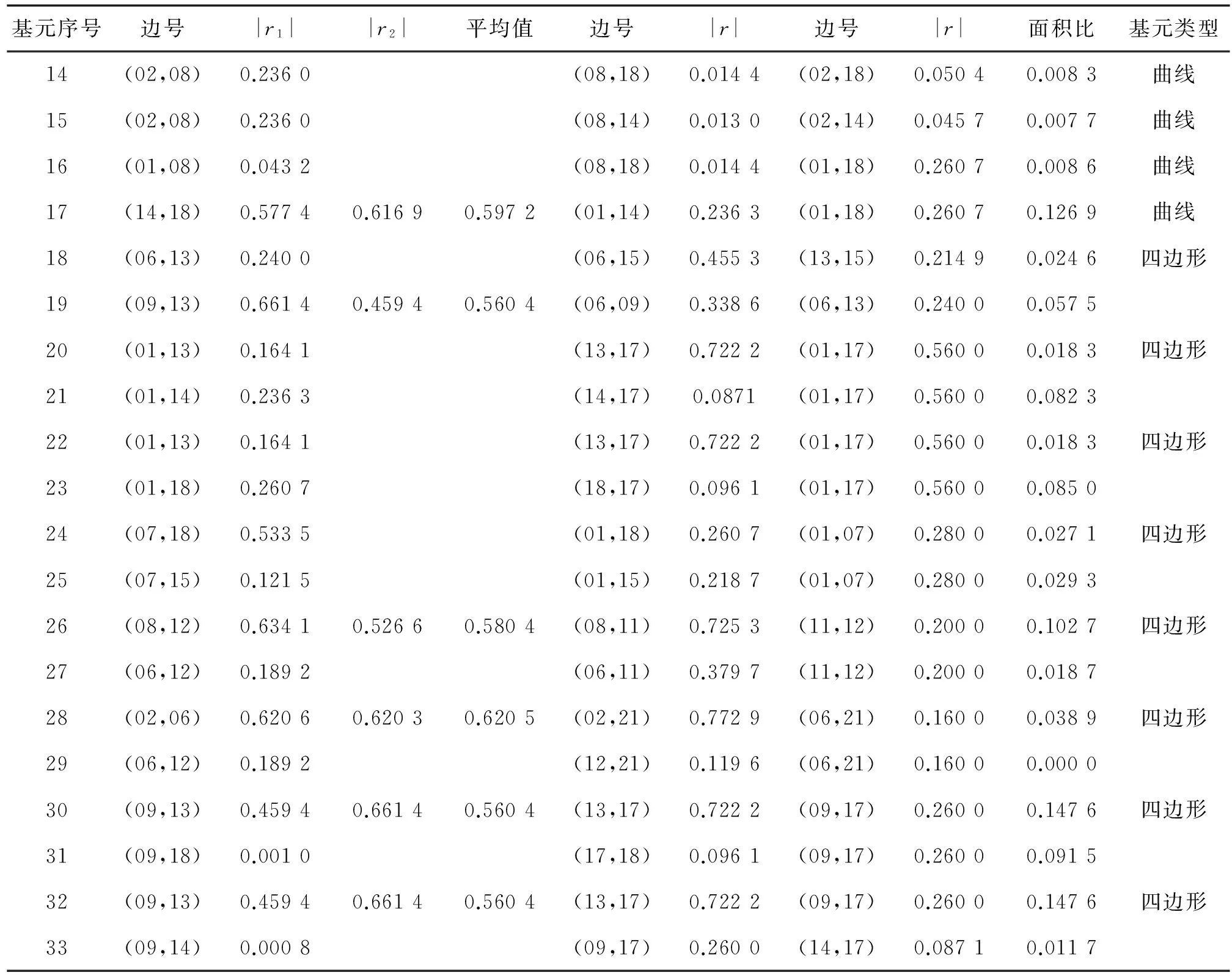
極大值約束
max{|l1,2-l1,3| (15) 相關性約束 |l2,3|<1,|l1,4|<1, (16) l=min{l1,4,l2,3}. (17) 假如l=l2,3,則由節點2、3、4與1、2、3構成的其中有一個三角形正好是2邊之和等于第3邊,為了滿足構成三角形的條件,節點2,3之間的相關系數應稍微大一些,故取l+0.1. 圖6 彌補相關連接線Fig.6 Supplement of related cables 圖7 城市生態系統網絡基元穩定性統計Fig.7 Statistics for the steadiness of urban ecosystem network unit 對于生態系統網絡的整體穩定性,可以有不同的思路和方法來計算,一種最為簡單的思路,就是考慮系統的平均穩定性.對于由多個網絡基元構成的生態系統網絡,若將每一個網絡基元看作整體網絡基本構成單位的一個抽樣,則全部樣本的穩定性的平均值,是可以來描述整體網絡的穩定性特征的. 對于均值的計算,可以有多種算法[13],比如算術平均、幾何平均、加權平均、調和平均等,當數據均為正數且對稱性較好時,可以考慮幾何平均法.圖7給出了計算機模擬計算的各種網絡基元的統計分析,由圖7可知,對于生態系統網絡基元,其統計特征為非對稱數據,綜合考慮其他幾種平均算法,選取幾何平均法作為計算總體平均的方法.假設某個網絡由n個單元相關三角形構成,根據幾何平均值可得整體網絡的穩定性,即 (18) 統計分析表明,當使用面積比作為指標進行穩定性計算時,其值多數會出現在0~0.2,和標準1相比,數據有偏低的趨勢. 表1 虛擬網絡基元面積比 上述以虛構網絡為例,對城市生態系統網絡穩定性進行了理論分析,下面以實際三線城市生態系統網絡為研究對象,進行穩定狀況分析.圖1中,三線城市的生態系統網絡由26個節點連接構建[11],由于原文獻中節點連線代表的是回歸系數,不能直接利用,為了計算穩定性,本文對數據做了進一步處理,將其表達為各指標間的相關系數(表2).考慮相關系數存在正負,本文取相關系數的絕對值計算,當2個節點構成雙向有向邊時,取雙向有向邊相關系數絕對值的平均值. 表2 三線城市部分指標之間相關系數及網絡基元面積比 續表2 由圖7可知,當以面積比作為城市生態系統網絡基元的穩定性指標時,其穩定性眾數出現在0.1附近,達到理想狀態1的可能性很小.實際計算三線城市生態網的總體均值,其值為0.044 4,對比圖7,介于0~0.2,屬于統計次數較多的區段,較為合理. 鑒于城市生態系統網絡的實際情況,一些指標之間沒有關聯,則這些節點之間不能構成網絡基元,在上述的計算中,尚未考慮.隨著城市的發展,城市生態系統也在不斷變化中,節點之間的關聯變化,可能導致舊指標的消失或者新指標的產生[12],對于城市生態系統網絡的演化,本計算方法仍然可以適用. [1] 范海燕.城市生態系統穩定性研究[D].蘇州:揚州大學,2011. FAN H Y.Research on stability of urban ecosystem[D].Suzhou:Yangzhou University,2011. [2] 劉臣輝,范海燕,詹曉燕,等.揚州城市生態系統穩定性分析[J].環境科學與技術,2011,34(4):110-114+119.DOI:10.3969/j.issn.1003-6504.2011.04.025. LIU C H,FAN H Y,ZHAN X Y,et al.Stability analysis of Yangzhou urban ecosystem[J].Environmental Science & Technology,2011,34(4):110-114+119.DOI:10.3969/j.issn.1003-6504.2011.04.025. [3] 李小方,鄧歡,黃益宗,等.土壤生態系統穩定性研究進展[J].生態學報,2009,29(12):6712-6722.DOI:10.3321/j.issn:1000-0933.2009.12.048. LI X F,DENG H,HUANG Y Z,et al .Advances in soil ecosystem stability[J].Acta Ecologica Sinica,2009,29(12):6712 - 6722.DOI:10.3321/j.issn:1000-0933.2009.12.048. [4] 廖玉靜,宋長春,郭躍東,等.三江平原濕地生態系統穩定性評價指標體系和評價方法[J].干旱區資源與環境,2009,23(10):89-94. LIAO Y J,SONG C C,GUO Y D,et al.Index system and methodology for wetland ecosystem stability in Sanjiang plain[J].Journal of Arid Land Resources and Environment,2009,23(10):89-94. [5] 王玲玲,曾光明,黃國和,等.湖濱濕地生態系統穩定性評價[J].生態學報,2005,25(12):3406-3410.DOI:10.3321/j.issn:1000-0933.2005.12.041. WANG L L,ZENG G M,HUANG G H,et al.Lake wetland ecosystem stability assessment[J].Acta Ecologica Sinica,2005,25(12):3406-3410.DOI:10.3321/j.issn:1000-0933.2005.12.041. [6] 李新旺,門明新,王樹濤,等.基于過程的河北平原農田生態系統穩定性評價[J].自然資源學報,2008,23(3):430-439.DOI:10.3321/j.issn:1000-3037.2008.03.009. LI X W,MEN M X,WANG S T,et al.An evaluation of stability of farm and ecosystem based on processes in Hebei plain[J].Journal of Natural Resources,2008,23(3):430-439.DOI:10.3321/j.issn:1000-3037.2008.03.009. [7] 趙志軒,金鑫,王凌河,等.基于動態因子的農田生態系統穩定性評價[J].華南農業大學學報,2010,31(4):22-26.DOI:10.3969/j.issn.1001-411X.2010.04.005. ZHAO Z X,JIN X,WANG L H,et al.Study on farmland ecosystem stability evaluation based on dynamic factors[J].Journal of South China Agricultural University,2010,31(4):22-26.DOI:10.3969/j.issn.1001-411X.2010.04.005. [8] 任平,洪步庭,程武學,等.長江上游森林生態系統穩定性評價與空間分異特征[J].地理研究,2013,32(6):1017-1024. REN P,HONG B T,CHENG W X,et al. Stability evaluation of forest ecosystem and study of spatial differential features in the upper Yangtze river[J].Geographical Research,2013,32(6):1017-1024. [9] 丁惠萍,張社奇,錢克紅,等.森林生態系統穩定性研究的現狀分析[J].西北林學院學報,2006,21(4):28-30+61.DOI:10.3969/j.issn.1001-7461.2006.04.007. DING H P,ZHANG S Q,QIAN K H,et al.Analysis of present scientific research in stability of forest ecosystem[J].Journal of Northwest Forestry University,2006,21(4):28-30+61.DOI:10.3969/j.issn.1001-7461.2006.04.007. [10] 趙秀勇.生產力發展與城市生態系統穩定性研究[D].南京:南京氣象學院,2003. ZHAO X Y.On coordination between urban ecosystem stability and the development of urban production forces[D].Nanjing:Journal of Nanjing Institute of Meteorology,2003. [11] 馬寨璞,安秋丹,劉慶朝.城市生態系統指標相互影響的定量研究[J].河北大學學報(自然科學版),2013,33(1):68-76.DOI:10.3969/j.issn.1000-1565.2013.01.014. MA Z P,AN Q D,LIU Q Z.Quantitative study of indicator interactions in urban ecological system[J].Journal of Hebei University(Natural Science Edition),2013,33(1):68-76.DOI:10.3969/j.issn.1000-1565.2013.01.014 . [12] 郭雷,許曉鳴.復雜網絡[M].上海:上海科技教育出版社,2006:1-445. [13] 李云雁,胡傳榮.試驗設計與數據處理[M].北京:化學工業出版社,2008. (責任編輯:趙藏賞) Theoretical computation and analysis of the stability of urban ecological system network MA Zhaipu1,ZHANG Kaili1,LI Shuaiqiang2,WANG Huixin1,WANG Mengmeng1 (1.College of Life Sciences,Hebei University,Baoding 071002,China;2.Overseas Products Department,Zhengzhou Yutong Bus Co.,Ltd,Zhengzhou 450061,China) In order to calculate the stability of urban ecosystem network,the structural characteristics of urban ecological system network is first analyzed,and the idea of computing the network stability is proposed based on the network unit.Then,the standard network unit and the concrete calculation method of its stability are defined;also the calculation method of overall network is discussed.At last,an example of ideal ecological system network is simulated which shows that the calculation method is feasible,and the method is further applied to the actual calculation of the third-tier urban ecological system network and a reasonable result is obtained. urban ecological system;network unit;network stability 10.3969/j.issn.1000-1565.2016.05.009 2015-12-11 河北省科技攻關計劃項目(06276902B) 馬寨璞(1970—),男,河北保定人,河北大學教授,主要從事生態模型及生物計算研究. E-mail:zhaipuma@hbu.edu.cn Q141 A 1000-1565(2016)05-0501-08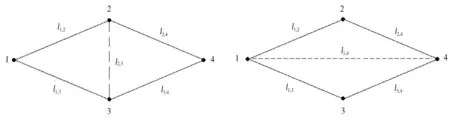
3 整體穩定性計算分析

4 應用與討論