函數置換條件下P-Ⅲ參數的最小二乘計算

唐榮桂王一帆盧曦

函數置換條件下P-Ⅲ參數的最小二乘計算

唐榮桂1王一帆2盧曦2

一、引言

眾所周知，因P-Ⅲ密度函數的原函數目前還無法求得，其參數只能應用一些估計的方法獲取，如矩法、三點法、極大似然法、權函數法、線性矩法和適線法等，大部分方法誤差大，有的隨意性大，可信度低。在尊重樣本的基礎地位和樣本誤差，同時考慮到散點函數擬合的準確度與唯一性的基礎上，筆者研究出在函數置換條件下利用最小二乘法原理進行P-Ⅲ參數計算的方法。

二、原理與方法

1.目標函數的建立

考察P-Ⅲ的密度函數：

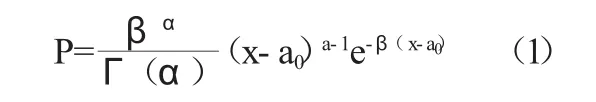
令u=x-a0，對于其中的指數函數y=e-βu，取區間[a，b]，區間內可近似用滿足兩端點連續（函數值相等）與平滑（一階導數值相等）的三次函數

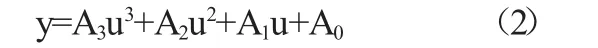
進行替代，三次函數的系數方程為：

對于發生在[a，b]內事件的概率為：

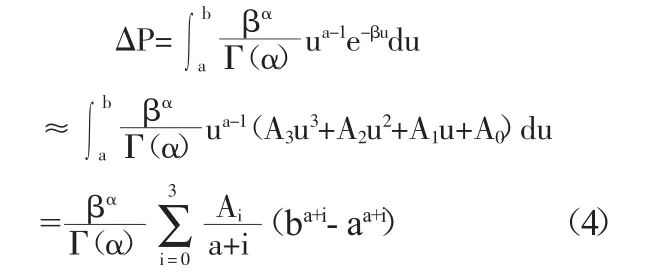
如果把P-Ⅲ的密度函數劃分成很多小區間，各個區間的概率依次為ΔPj，就有如下累積概率公式：

對應于P-Ⅲ的密度函數，樣本系列序號i從有限端（小）到無限端（大）排列，給出如下樣本的有關計算公式：

這樣就可以根據公式（2）-（6）計算樣本的累積頻率Pei、模比系數Ki、有限端點坐標a0、平移后坐標ui（以0為起點）、部分概率ΔPi以及理論上的累積概率Pti。若要達到樣本點與理論曲線的最佳擬合，根據誤差的最小二乘原理，必然滿足如下目標函數：

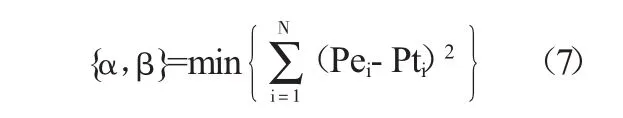
（7）式是多系數的復合函數方程式，沒有辦法利用求導數的辦法建立參數方程組，也就不可能用樣本統計計算的方法求解參數。下面將研究（7）式解的問題。

2.P-Ⅲ參數解的唯一性

P-Ⅲ的密度函數有3個部分組成，冪函數控制增率，指數函數控制減率，常數項是保證全體事件的概率為1的約束條件。因此，密度函數對于α始終是增函數，對于β又始終是減函數，都具有單調性，它們對分布函數的影響同樣具有單調性，因此，對于固定樣本，（7）式成立時兩個參變量必然只有唯一的平衡點，即（7）式只有唯一解。

3.簡單的求解方法——方向搜索法

如果利用計算機程序，依據（7）式，以不同的參數組合（排除不符合P-Ⅲ特征）進行計算，尋找到最小值，即可獲得目標函數的解。這里再給出簡單的解法——方向搜索法（只適用于具有單調性質的參數），該方法可以減少大量的計算工作量，快速獲得高精度結果。具體步驟如下：

①選定方程可能解的初值，如P-Ⅲ參數，可以利用其他方法給出的估計值作為初值；

②根據精度要求，設定參數的變化步長，可以一輪搜索，也可以多輪搜索；

③以一個參數固定，另一參數變化，通過（6）計算出數值，向數值減少方向逐步搜索到最小值點；

④再以該點為中心計算其他6個方位點上的值，如果沒有比其更小的值，該點對應的參數即為所解。如果有比其還小的點，就沿著這兩個數值較小的點的減少方向繼續搜索，直至沒有更小的值為止。

三、應用舉例

以江蘇省白馬湖地區（高良澗閘、運東閘、阮橋閘三站平均）最大3日雨量的P-Ⅲ參數計算為例。這里主要介紹應用

excel完成的計算過程。

1.制作誤差平方和計算模板（excel工作簿）

該簿由兩塊組成。

第一塊：坐標平移計算和各個區間置換公式系數計算。樣本38年，變量u從0到38將密度曲線分成38個部分，建立38張工作表（1-38），每張表有一個固定部分和一個活動部分。

固定部分，設立α、β輸入窗口，當參數改變，密度函數的起點坐標和各樣本點的距0值需要相應計算。38張表的這部分都相同（直接復制），但表（2-38）的兩個輸入窗口改為調用表1相應單元格的值。

活動部分，目的是分別計算兩點間置換函數的系數，這里調用了excel行列式計算函數，同樣復制表（1）的活動部分，后面各表只需在相同的列號欄依次向下移動一行進行粘貼即可。

第二塊：誤差平方和計算。工作簿中，專門設置一張計算誤差平方和的表格。在公式輸入時，α、β必須調用表1的指定單元格數據，Γ（α）可調用excel中的GAMMALN函數，ΔPi中各行的置換函數系數可依次調用表（1-38）中的相同單元格的數據（用活動單元格，僅需改動工作表號）。在表格的最末端有一個誤差平方總和欄，它是整個工作簿的輸出窗口，α、β變動后的數字就取自該單元格。

2.方向搜索

根據誤差平方和最小來找出指定精度下的P-Ⅲ參數。

第一步：選擇參數初始值。利用武漢大學提供的《水文頻率分布曲線適線軟件》求得的樣本的參數為，本文計算中使用的是模比系數，x=1，利用公式（8）計算得：α=4，β=5.9。

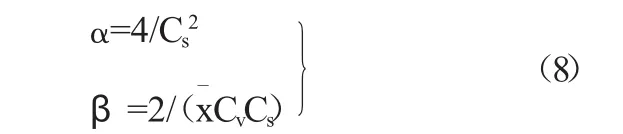
第二步，選擇適合的步長進行搜索。按照三位有效數字精度，分2次搜索。由于計算的誤差平方和隨著參數的變化規律明顯，只需要選擇代表性點，按照一定方向，很快就能取得結果。

粗搜索：以初始值為定點，先縱向搜索，找到最小值點，再向臨側逐步找最小值點。經過初步搜索，可以確定最小值在3.25〈α〈3.35及4.85〈β〈4.95區間內。

精搜索：按照給定精度的最小單位作為表格的計算單位，以粗搜索得出的最小值點為定點，先縱向后橫向進行搜索。根據最小值點得出：α=3.32，β=4.92，據此換算出江蘇省白馬湖地區最大3日降水量的P-Ⅲ參數為：

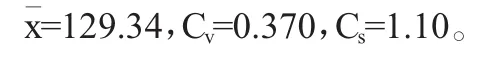
3.成果驗證

為了檢驗本文方法，下面給出兩種方法擬合圖進行對照，見圖1。

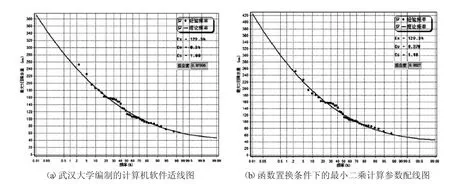
圖1 江蘇省白馬湖地區最大3日降水量頻率曲線對照圖

計算機軟件計算得到的參數應該優于其他方法的估計值，本文方法的擬合度（0.983）優于計算機軟件適線的擬合度（0.978）；點線配合情況看，本文方法做到了兼顧全部樣本，略優于計算機軟件配線；以200年一遇的設計標準為例，軟件方法比本文方法偏小6.2%，這個差別對該區域的排澇設計帶來的影響還是很大的。

4.誤差評估

與直接進行最小二乘法計算相比，本方法唯一的誤差來源是函數置換，為檢驗其影響，取本文的最終結果β=4.92來驗證。方法：模比系數以0.001為步長，用對應的分段函數和指數函數來計算相對誤差，得出的結果是：負偏為主，平均誤差：-0.61‰，最大偏離-4.7‰，最大偏離區間在u36～u38（該區間平均偏離值-2.0‰），一般偏離數值與間距同步，若間距在0.03以下時，偏差小于十萬分之一。就本例的情況，總體影響小于千分之一，可以忽略。

四、關于本文方法與常規方法比較

目前評判P-Ⅲ參數優劣，主要通過視覺觀察點線配合情況，按說幾率格紙繪制P-Ⅲ曲線是無法用簡單的數學解析式表達，依靠視覺調試（適線法）當然會造成很大誤差，還可能出現與P-Ⅲ理論相悖的結果。另外現行方法對設計值推算也很麻煩，一般的查用表又很粗糙，對非專業人員來說，使用P-Ⅲ有一定難度。

本文方法是建立在P-Ⅲ理論基礎之上，實測樣本配線又是用公認的最小二乘準則，數學理念清晰，且結果唯一，不會造成歧義。為了滿足視覺效果，也可以繪制累積頻率點和擬合的Ki～Pti線加以參照。

利用本文方法編制簡單的小程序（需將置換函數的間距設計的很小），可以方便求出高精度的P-Ⅲ參數，還可以根據參數及設計標準輸出設計結果。作者相信，隨著技術的發展，P-Ⅲ也會和其他函數一樣成為各種計算工具的內置函數，方便人們的應用■

（作者單位：1.江蘇省洪澤湖水利工程管理處2231002.江蘇省灌溉總渠管理處223200）