基于局部均值分解與拉普拉斯特征映射的滾動軸承故障診斷方法

徐倩倩 劉 凱 侯和平 徐卓飛

西安理工大學，西安，710048

?

基于局部均值分解與拉普拉斯特征映射的滾動軸承故障診斷方法

徐倩倩 劉 凱 侯和平 徐卓飛

西安理工大學，西安，710048

針對滾動軸承非平穩振動信號的特征提取及維數優化問題，提出了融合局部均值分解與拉普拉斯特征映射的軸承故障診斷方法。首先，通過局部均值分解對非平穩振動信號進行平穩化分解，提取乘積函數分量、瞬時頻率及瞬時幅值的高維信號特征集；然后，將高維特征集作為拉普拉斯特征映射算法的學習對象，提取軸承高維故障特征集的內在流形分布，以獲得敏感、穩定的軸承振動特征參數，實現基于非平穩振動信號分析的滾動軸承故障特征提取；最后，結合支持向量分類模型量化LMD-LE方法的特征提取效果，實現不同狀況下的軸承故障分類。軸承故障樣本分類識別平均正確率達到91.17%，表明LMD-LE方法有效實現了高維局部均值分解特征集合的降噪，所提取的特征矩陣對軸承故障特征描述準確。

非平穩信號；局部均值分解；拉普拉斯特征映射；故障診斷

0 引言

滾動軸承是旋轉機械中最常用也是最易損壞的零部件。據統計，旋轉機械中30%的故障是由軸承缺陷引起的。因此，對滾動軸承進行工況監測和故障診斷是非常必要的。然而在工程實際應用中，軸承的運行狀態是動態變化的，尤其在設備故障突發期間，機械系統的驅動力、阻尼力及彈性力等動力學參數呈現非線性變化，往往會導致所觀測的振動信號表現出較強的非平穩特性。

局部均值分解 (local mean decomposition, LMD) 方法是一種自適應時頻分析方法，通過自適應的信號分解和降噪能力兼顧了信號在時域和頻域的局部化特征和全貌。相比線性時頻分析、雙線性時頻分析及參數化時頻分析方法[1]，LMD可解決固定類型基函數可能會產生虛假的時頻信息問題、多參數優化導致計算量大問題及Heisenberg原理在時頻域的限制性問題, 在軸承故障信號處理中應用廣泛。文獻[2-7]應用LMD處理軸承振動信號，取得了較好的應用效果；文獻[8-11]分別將LMD與非局部均值去噪、雙樹復小波降噪、奇異值差分譜、改進形態濾波法結合，實現了振動信號及分量的降噪處理；文獻[12-15]分別利用馬氏距離、灰色相似關聯度、變量預測模型、隱馬爾可夫模型等故障分類方法實現了基于LMD的軸承故障分類。

然而，在信號分量中提取的豐富信號特征集往往存在著大量冗余信息和相關信息，反而會彼此干擾并產生模式混淆，在很大程度上影響故障模式識別的效果。因此，有必要對冗余信號特征集進行維數優化處理以實現數據降噪。但現有基于LMD的軸承故障診斷方法并未對高維特征矩陣進行優化處理，故本文進一步提出了融合LMD與拉普拉斯特征映射(Laplacian eigenmap,LE)算法的軸承故障診斷方法，將局部均值分解的特征集合作為LE算法的高維特征輸入，完成高維特征集的準確提取，最終實現不同故障程度、不同故障類型的軸承故障分類。

1 基于LMD的非平穩信號分解

近年來，眾多學者提出了一些結合復雜信號自身特點的自適應分解時頻分析方法，其中應用最為廣泛的是經驗模態分解(empirical model decomposition, EMD)。LMD是由EMD方法原理發展而來的，可以有效解決EMD有可能產生的物理意義無法解釋的瞬時頻率問題，避免EMD的過包絡和欠包絡問題，成為現有自適應時頻分析方法的研究熱點。對于任意檢測信號x(t)，其LMD算法步驟如下。

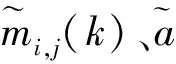
(1)

(2)

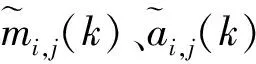
(3)

(4)

然后，分別計算瞬時幅值ai(t)、瞬時頻率fi(t)及信號分量PFi(t)，并獲得新的信號ui(t)=x(t)-PFi(t)，若ui(t)不是單調函數，則將ui(t)作為新的信號重復上述步驟，直至ui(t)滿足單調函數條件。即

(5)

PFi(t)=ai(tj)si,j(t)

(6)

fi(t)=d(arccos(si,j(t)))/(2πdt)

(7)

最終，LMD通過三重循環將x(t)分解為一系列PFi(t)分量與余項ui(t)的和，將非平穩信號的特征提取問題轉換為平穩分量的特征提取問題。即

x(t)=∑PFi(t)+ui(t)

(8)

2 基于LE的故障特征集維數優化

現有的高維數據降維方法可分為線性降維方法、基于核函數的非線性降維方法以及基于特征值的非線性降維方法，其代表性方法分別為主元分析(principle component analysis, PCA)法、核主元分析(kernel principle component analysis, KPCA)法及LE算法。研究表明LE算法適用于設備工況特征的高維數據的非線性特征挖掘和降維，并取得了良好的去冗余效果[16-19]。

根據圖譜理論，如果數據均勻采樣自高維空間中的低維流形，流形上的拉式算子可以由圖上的Laplacian逼近，而圖上最前面的幾個特征向量就是流形上 L-B算子特征函數的離散逼近，最終實現高維流形的最優嵌入。若第i個節點xi和第j個節點xj之間有邊連接，由熱核法確定邊的權值為

Wij=exp(-‖xi-xj‖2/σ2)

(9)

構建拉普拉斯特征矩陣L=D-W,假設構建的近對鄰圖是連通的，那么尋找低維嵌入的問題就歸結為對廣義特征向量問題的求解：

Ly=λDy

(10)

可見，LE算法通過對矩陣特征值和特征向量的求解實現了特征集的降維和特征提取，不需要進行迭代運算，減小了計算量，縮短了算法運行時間。為有效實現高維軸承故障特征集的維數優化，獲得故障特征的精確描述，本文采用LE算法進行軸承故障冗余特征集處理，通過對高維非線性數據進行降維，從高維非線性數據中找出隱藏在高維觀測空間數據中的低維結構表示，揭示數據的內在流形分布。

3 LMD與LE融合算法

如圖1所示，基于LMD和LE的軸承故障診斷方法步驟如下：

(1)根據LMD算法對多樣本軸承故障信號x(t)進行LMD分解。獲得信號分量曲線PFi、瞬時幅值曲線a及瞬時頻率曲線f。依據峭度最大原則選擇PF1作為故障特征頻帶[22]，分別提取PF1曲線的波形指標、裕度指標、峭度指標、脈沖指標、峰值指標共5個時域特征及PF1、a1、f1曲線的均方根值、絕對平均值、方根幅值、峭度、偏斜度、峰-峰值共6個線型特征，構成23維故障特征集X。

(2)根據LE算法對特征集X進行維數優化。將23維故障特征集作為LE算法的高維特征輸入，選用K近鄰域(KNN)法構建近鄰圖G，計算高維矩陣X映射到低維空間的權重矩陣W及拉普拉斯特征矩陣L的特征向量構成的低維坐標矩陣T。

(3)通過SVM分類模型完成軸承故障樣本的分類識別。將特征映射矩陣T作為軸承故障樣本特征參數，由多類故障數據集構成SVM模型的訓練樣本及測試樣本，通過模型參數的交叉驗證尋優完善SVM模型，實現多類軸承故障的分類識別。

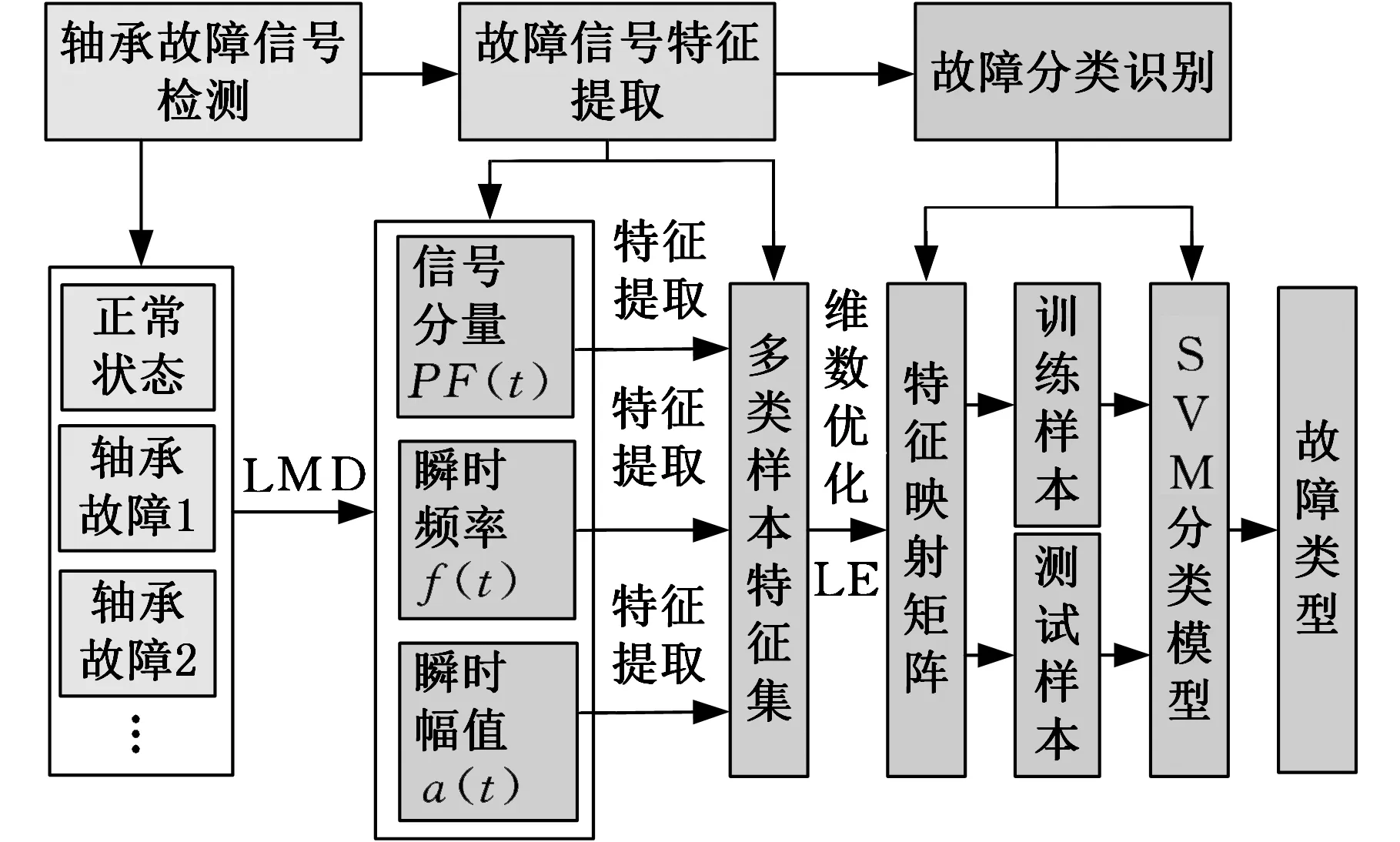
圖1 基于LMD和LE的軸承故障診斷方法

4 SKF6205-2RS軸承故障實驗

SKF6205-2RS型滾動軸承實驗中采用的數據均來自美國凱斯西儲大學電氣實驗室的軸承故障數據庫。電機負載約1470 W,轉速為1750 r/min，采樣頻率為12 kHz，其傳感器位置為驅動端的軸承座上垂直位置。損傷程度a、b、c分別代表0.178 mm、0.356 mm、0.533 mm，軸承故障A、B、C、D分別代表正常狀態及不同損傷程度下故障、滾動體故障、內圈故障、外圈故障，建立故障數據庫：

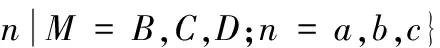
其中，M.n表示n損傷程度下的M類故障數據，具體故障樣本分組見表1。

表1 實驗數據分組

在本實驗中，以軸承轉一圈所采集的數據點數的兩倍作為確定樣本長度的參考[23]，則軸承正常及各種故障狀態下的數據采樣長度N=1000，樣本數為100。圖2～圖4所示分別為軸承滾動體故障、內圈故障及外圈故障數據經LMD獲得的PF1、a1、f1曲線。提取軸承每組故障信號的100個樣本構成100×23維故障數據集，作為降維算法的高維特征集輸入。

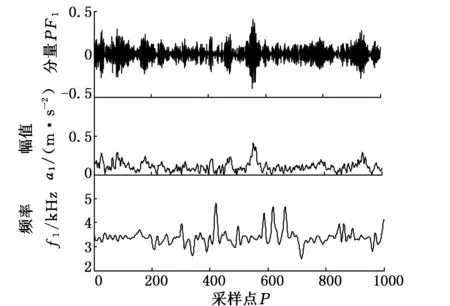
圖2 PF1、a1、f1 曲線(滾動體故障)

圖3 PF1、a1、f1 曲線(內圈故障)

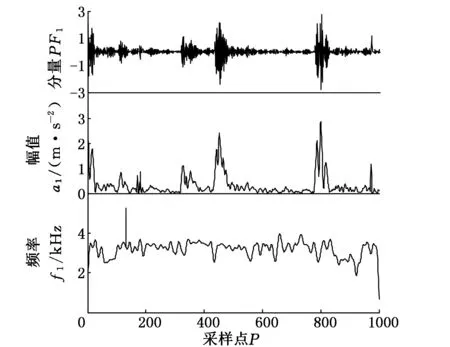
圖4 PF1、a1、f1 曲線(外圈故障)

分別采用PCA、KPCA及LE算法對軸承狀態特征矩陣進行維數優化處理，選取優化目標維數為3。圖5～圖10所示分別為故障集1～故障集6的LMD特征降維效果。

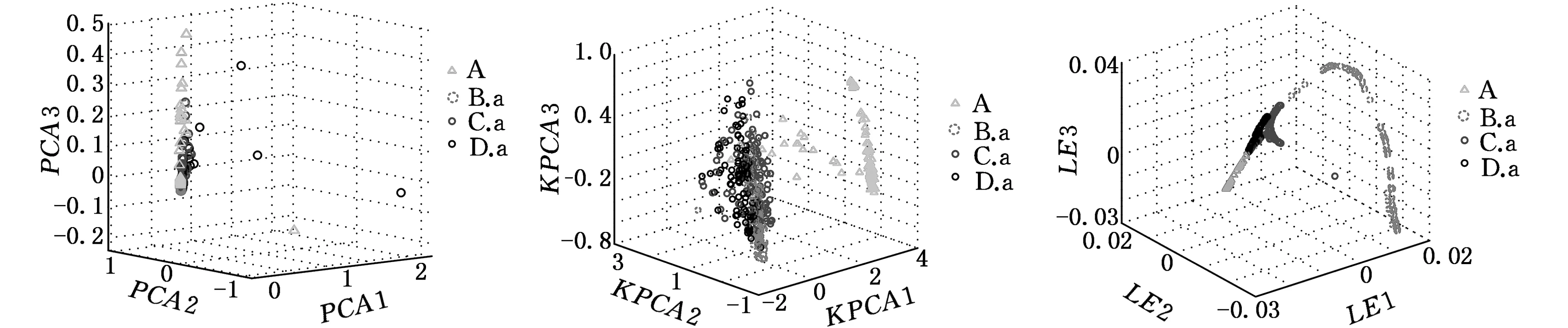
(a)PCA (b)KPCA (c)LE圖5 三種降維方法對LMD特征聚類效果(故障集1)

(a)PCA (b)KPCA (c)LE圖6 三種降維方法對LMD特征聚類效果(故障集2)

(a)PCA (b)KPCA (c)LE圖7 三種降維方法對LMD特征聚類效果(故障集3)

(a)PCA (b)KPCA (c)LE圖8 三種降維方法對LMD特征聚類效果(故障集4)

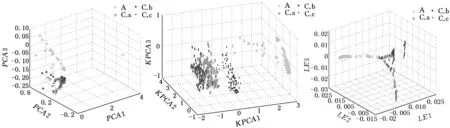
(a)PCA (b)KPCA (c)LE圖9 三種降維方法對LMD特征聚類效果(故障集5)

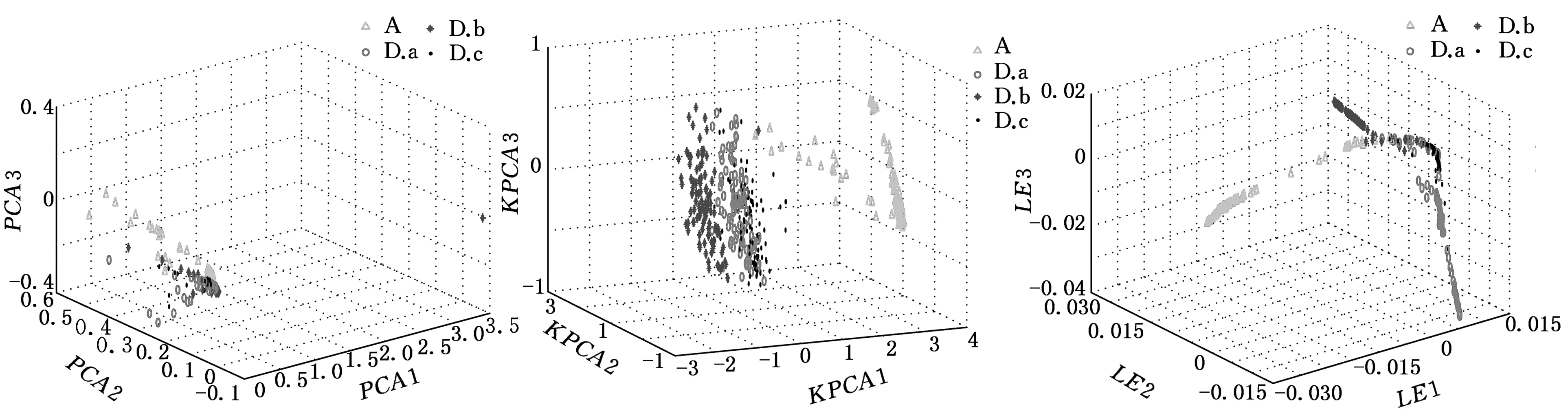
(a)PCA (b)KPCA (c)LE圖10 三種降維方法對LMD特征聚類效果(故障集6)

由圖5～圖10對比發現，三種方法都成功分離出正常樣本數據，但對其余三類樣本的聚類效果并不相同：PCA方法處理使得不同工況樣本類內距最小，有效實現了同類樣本的聚集，但類間距最小，無法區分出不同類別故障樣本，樣本聚類可視化效果差；KPCA方法相比PCA方法，擴大了類間距，不同類樣本的分離效果略有提高，但是不同類別樣本重合度高，使得樣本聚類效果變差，增加了軸承故障診斷的復雜度；LE方法相比前兩種方法，類間距明顯增大，樣本點雖有重合但樣本聚類效果最強，故障特征更具有代表性，有利于軸承故障類型的診斷識別。

可見，基于特征的LE降維方法對不同類型樣本的類間距最大，分類識別效果優于線性降維及基于核函數的降維方法。故本文選取LE算法對LMD特征集進行維數優化，去除特征向量間的冗余性，降低軸承故障分類識別的復雜度。

為量化LMD-LE方法的特征提取效果，本文結合支持向量機(SVM)作為故障類型的分類識別工具。取每類故障的前50組樣本作為訓練矩陣，并對后50組樣本作為測試樣本進行類型預測，測試樣本正確識別率見表2。可見7組故障集的測試樣本識別正確率平均達到91.17%：故障集1～故障集3代表同一故障程度下的滾動體、內圈、外圈故障，其測試樣本識別正確率達到92%以上，說明本文方法對不同類軸承故障特征提取效果明顯；故障集4～故障集6代表不同故障程度下同一類故障，其測試樣本識別正確率略低于不同類故障的識別率，測試樣本的故障類型與預測結果基本吻合；故障集7屬于不同故障程度、不同故障類型下的復雜多類別故障分類問題，在分類正確率上低于前6組故障集。圖11為第7組故障集的測試樣本類型預測圖，錯誤分類樣本均勻分布在多個故障樣本中，屬于全局性問題，或由信號噪聲、算法誤差造成，但分類正確率仍達到85%以上，基本實現了復雜故障樣本的分類。

表2 SVM測試樣本識別正確率

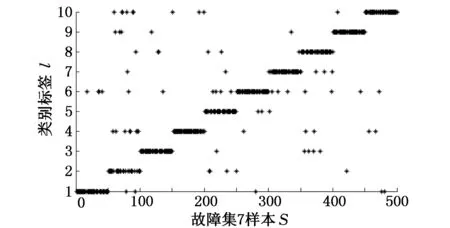
圖11 第7組測試樣本分類預測結果

5 結論

(1)LE方法在去除故障特征集合的冗余性方面具有明顯優勢。

(2)LMD與LE的融合應用對滾動軸承故障特征提取效果良好，降低了故障特征集的復雜程度，為非平穩振動信號特征參數提取提供了新的方法。后續研究應結合信號濾波降噪法對振動信號進行預處理，更進一步提高特征提取準確性。

[1] 唐友福.基于廣義局部頻率的非線性非平穩信號故障特征提取方法研究[J].機械工程學報,2015,51(11):81-81. Tang Youfu. Study on Fault Feature Extraction for Nonlinear Nonstationary Signals Based on General Local Frequency[J]. Journal of Mechanical Engineering, 2015, 51(11): 81-81.

[2] 陳保家,何正嘉,陳雪峰，等.機車故障診斷的局域均值分解解調方法[J].西安交通大學學報,2010,44(5):40-44. Chen Baojia, He Zhengjia, Cheng Xuefeng,et al. Locomotive Fault Diagnosis Based on Local Mean Decomposition Demodulating Approach [J]. Journal of Xi’an Jiaotong University, 2010,44(5):40-44.

[3] 楊宇,王歡歡,程軍圣，等.基于LMD的包絡譜特征值在滾動軸承故障診斷中的應用[J].航空動力學報,2012,27(5):1153-1158. Yang Yu, Wang Huanhuan, Cheng Junsheng, et al. Application of Envelope Spectrum Characteristics Based on LMD to Roller Bearing Fault Diagnosis[J].Journal of Aerospace Power,2012,27(5):1153-1158.

[4] 侯蒙蒙,許同樂,高朋飛，等.基于LMD分解的風機軸承故障信號提取研究[J].中國農機化學報,2015,36(2):277-279. Hou Mengmeng, Xu Tongle, Gao Pengfei, et al. Methods of Bearing Fault Characteristic Signal Extraction[J]. Journal of Chinese Agricultural Mechanization，2015,36(2):277-279.

[5] 程軍圣,楊怡,楊宇，等.基于LMD的能量算子解調機械故障診斷方法[J].振動、測試與診斷,2012,32(6):915-919. Cheng Junsheng, Yang Yi, Yang Yu, et al. Mechanical Fault Diagnosis Method of Energy Operator Demodulating Approach Based on LMD[J].Journal of Vibration Measurement & Diagnosis,2012,32(6):915-919.

[6] 王衍學,何正嘉,訾艷陽，等.基于LMD的時頻分析方法及其機械故障診斷應用研究[J].振動與沖擊,2012,31(9):9-12. Wang Yanxue,He Zhengjia,Zi Yanyang, et al.Several Key Issues of Local Mean Decomposition Method Used in Mechanical Fault Diagnosis[J]. Journal of Vibration and Shock, 2012,31(9):9-12.

[7] 黃浩,呂勇,肖涵，等.基于PCA和LMD分解的滾動軸承故障特征提取方法[J].儀表技術與傳感器,2015(4):76-78. Huang Hao, Lü Yong, Xiao Han, et al.Feature Extraction Method of Rolling Bearing Fault Based on Principal Component Analysis and Local Mean Decomposition[J]. Instrument Technique and Sensor, 2015(4):76-78.

[8] 祝青林,呂勇,李寧，等.非局部均值去噪和LMD綜合的滾動軸承故障診斷[J].機床與液壓,2015,43(13):172-176. Zhu Qinglin,Lü Yong, Li Ning, et al.Fault Diagnosis to Rolling Bearing by Integration of Nonlocal Means De-noising and LMD[J]. Machine Tool & Hydraulics, 2015,43(13):172-176.

[9] 侯蒙蒙,許同樂.基于DT-LMD機床軸承故障信號提取研究[J].機床與液壓,2015,43(7):185-188. Hou Mengmeng, Xu Tongle. Study of Bearing Fault Signal Extraction of Machine Tool Based on DT-LMD[J]. Machine Tool & Hydraulics,2015,43(7):185-188.

[10] 馬朝永,劉茜,段建民，等.基于LMD與奇異值差分譜的滾動軸承故障診斷方法[J].北京工業大學學報,2014,40(2):182-188. Ma Chaoyong, Liu Qian, Duan Jianmin, et al.Fault Diagnosis Method of Rolling Bearings Based on LMD and Singular Value Difference Spectrum[J]. Journal of Beijing University of Technology, 2014,40(2):182-188.

[11] 馮研研,艾延廷,周海侖，等.改進形態濾波與LMD結合的滾動軸承故障診斷方法研究[J].機械設計與制造,2015(1): 83-86. Feng Yanyan, Ai Yanting, Zhou Hailun,et al. Study on Improved Morphological Filter and LMD Fault Diagnosis of Roller Bearing[J]. Machinery Design & Manufacture, 2015(1):83-86.

[12] 葛明濤,董素鴿.LMD及馬氏距離敏感閾值的滾動軸承故障診斷[J].機械設計與制造,2015(2):210-213. Ge Mingtao, Dong Suge. Fault Diagnosis Method of Rolling Bearings Based on LMD and Mahalanobis Distance Sensitive Threshold [J]. Machinery Design & Manufacture, 2015(2):210-213.

[13] 程軍圣,羅頌榮,楊斌，等.LMD能量矩和變量預測模型模式識別在軸承故障智能診斷中的應用[J].振動工程學報,2013,26(5):751-757. Cheng Junsheng, Luo Songrong, Yang Bin, et al. LMD Energy Moment and Variable Predictive Model Based Class Discriminate and Their Application in Intelligent Fault Diagnosis of Roller Bearing [J]. Journal of Vibration Engineering,2013,26(5):751-757.

[14] 孟宗,閆曉麗,王亞超.基于LMD和HMM的旋轉機械故障診斷[J].中國機械工程,2014,25(21):2942-2946. Meng Zong, Yan Xiaoli, Wang Yachao. Rotating Machinery Fault Diagnosis Based on Local Mean Decomposition and Hidden Markov Model[J]. China Mechanical Engineering,2014, 25 (21):2942-2946.

[15] 裴峻峰,于志遠,董雪，等.基于LMD和灰色相似關聯度的軸承故障診斷方法[J].機械設計與制造,2015(4):66-69. Peng Junfeng, Yu Zhiyuan, Dong Xue, et al. Roller Bearing Fault Diagnosis Method Based on LMD and Grey Similar Incidence[J]. Machinery Design & Manufacture, 2015(4):66-69.

[16] 賈茂林,王孫安,梁霖.利用非線性流形學習的軸承早期故障特征提取方法[J].西安交通大學學報,2010,44(5):45-49. Jia Maolin, Wang Sun’an, Liang Lin. Feature Extraction for Incipient Fault Diagnosis of Rolling Bearings Based on Non-linear Manifold Learning[J]. Journal of Xi’an Jiaotong University,2010,44(5):45-49.

[17] 趙斐,陸寧云,楊毅，等.基于工況識別的注塑過程產品質量預測方法[J].化工學報,2013,64(7):2526-2534. Zhao Fei, Lu Ningyun, Yang Yi, et al. Product Quality Prediction Method for Injection Molding Process Based on Operating Mode Recognition[J]. CIESC Jorunal,2013,64(7):2526-2534.

[18] 劉海濤,汪增福,曹洋，等.基于流形學習的三維步態魯棒識別方法[J].模式識別與人工智能,2011,24(4):464-472. Liu Haitao, Wang Zengfu, Cao Yang, et al. 3D Robust Gait Recognition Based on Manifold Learning[J]. Pattern Recognition and Artificial Intelligence,2011,24(4):464-472.

[19] 李月仙,韓振南,黃宏臣，等.基于拉普拉斯特征映射的旋轉機械故障識別[J].振動與沖擊,2014,33(18):21-25. Li Yuexian, Han Zhennan, Huang Hongchen, et al. Fault Diagnosis of Rotating Machineries Based on Laplacian Eigenmaps[J].Journal of Vibration and Shock, 2014,33(18):21-25.

[20] He Qingbo. Vibration Signal Classification by Wavelet Packet Energy Flow Manifold Learning[J].Journal of Sound and Vibration,2013,332(7):1881-1894.

[21] He Qingbo. Time-frequency Manifold for Nonlinear Feature Extraction in Machinery Fault Diagnosis[J]. Mechanical Systems and Signal Processing,2013,35(1/2):200-218.

[22] 李宏坤, 趙長生,周帥，等. 基于小波包-坐標變換的滾動軸承故障特征增強方法[J].機械工程學報, 2011,47(19):74-80. Li Hongkun, Zhao Changsheng, Zhou Shuai, et al. Fault Feature Enhancement Method for Rolling Bearing Based on Wavelet Packet-coordinate Transformation[J].Journal of Mechanical Engineering, 2011,47(19):74-80.

[23] 張媛,秦勇,邢宗義，等.基于LMD-PCA-LSSVM的滾動軸承安全域估計和狀態辨識方法[J].振動與沖擊,2013,32(20): 172-178. Zhang Yuan, Qin Yong, Xing Zongyi, et al.Safety Region Estimation and State Identification of Rolling Bearings Based on LMD-PCA-LSSVM[J]. Journal of Vibration and Shock, 2013, 32(20):172-178.

(編輯 陳 勇)

Fault Diagnosis Method of Bearings Based on LMD and LE

Xu Qianqian Liu Kai Hou Heping Xu Zhuofei

Xi’an University of Technology, Xi’an, 710048

A new diagnosis method for feature extraction of non-stationary vibration signals and fault classification of rolling bearings was proposed based on LMD and LE. Firstly, the non-stationary vibration signals of rolling bearings were decomposed into several product functions with LMD. Then, dimensional fault feature sets were established by the time-frequency domain features of product function, instantaneous frequency and amplitude. Secondly, LE was introduced to extract the sensitive and stable characteristic parameters to describe the running states of rolling bearings effectively and accurately. Finally, support vector machine classification model was built to realize the classification of fault bearings. For test samples classification, the average prediction accuracy is as 91.17%.It means that the fusion method of the LMD and LE is suitable and feasible for the bearing fault feature extraction.

non-stationary signal; local mean decomposition(LMD); Laplacian eigenmap(LE); fault diagnosis

2015-10-21

國家自然科學基金資助項目(51275406)；國家青年科學基金資助項目(51305340)

TH17

10.3969/j.issn.1004-132X.2016.22.016

徐倩倩，女，1989年生。西安理工大學機械與精密儀器工程學院博士研究生。主要研究方向為機械狀態信號處理、故障診斷。劉 凱，男，1957年生。西安理工大學機械與精密儀器工程學院教授、博士。侯和平，男，1978年生。西安理工大學印刷包裝與數字媒體學院副教授、博士研究生。徐卓飛，男，1985年生。西安理工大學印刷包裝與數字媒體學院講師、博士。