考慮參數相關性的結構二階可靠性分析方法

姜 潮 鄧青青 張 旺

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

?

考慮參數相關性的結構二階可靠性分析方法

姜 潮 鄧青青 張 旺

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

提出了一種基于vine copula函數的二階可靠性分析方法(VC-SORM)，為存在復雜多維相關性的結構可靠性分析提供了有效手段。通過vine copula函數將隨機向量多維概率分布函數轉換為多個二維copula函數，基于極大似然估計法和AIC信息準則對各二維copula函數進行最優化選擇，從而構建出聯合概率分布函數，并進行一階可靠性分析；在一階可靠性分析的基礎上，對功能函數進行二階近似，獲得精度更高的可靠性分析結果。最后通過兩個數值算例驗證了該方法的有效性。

結構可靠性；vine copula函數；二階可靠性分析方法；參數相關性

0 引言

在結構可靠性分析領域，通常使用概率模型描述載荷、材料屬性、結構尺寸等存在的不確定性。基于概率模型，已發展出了一系列有效的可靠性分析方法，如一次二階矩法(first order reliability method, FORM)[1]、二次二階矩法(second order reliability method, SORM)[2]、體系可靠性分析[3]、響應面法[4]、蒙特卡羅(Monte Carlo)方法[5]等。現有可靠性方法很多時候假設各隨機變量相互獨立，并轉換到標準正態空間進行求解。然而，在很多實際工程問題中，隨機變量間具有相關性[6]，且變量間的相關性可能對可靠性分析結果產生很大影響。目前處理相關性的可靠性方法主要有Nataf變換[7]和Rosenblatt變換[8]。Nataf變換用邊緣分布和相關系數矩陣將多維相關非正態變量轉換為標準獨立正態變量進行處理，在可靠性領域已經得到廣泛應用[9-10]。然而Nataf變換僅考慮了變量間的線性相關性，只能在某些特定樣本分布的情況下較好地度量變量間相關性；當很多樣本分布類型或者變量間的聯合分布函數不服從高斯分布時，該方法可能存在較大誤差[11]。理論上，Rosenblatt變換是一種精確的相關性處理方法，它對輸入隨機變量取條件將原相關變量轉換為標準獨立正態變量,但是，Rosenblatt變換必須基于精確的聯合概率分布函數，而實際工程中多維隨機變量的聯合概率分布函數通常是未知的，所以其實際應用受到較大限制。

近年來，在不確定性分析領域已出現了一種處理隨機變量相關性的有效數學工具，即copula函數。copula函數最早由Sklar[12]提出，它可以被視為一種邊緣分布和聯合分布之間的連接函數[13]，可用于建立具有相關性的隨機向量的聯合分布函數。copula函數已經在金融和水文等領域得到大量應用[14-15]，因為其在處理隨機相關性方面的強大功能，近年來被逐漸引入結構可靠性領域。Lebrun等[11,16]證明了在可靠性領域常用的Nataf變換可等效為Gaussian copula函數，并比較了在二維copula情況下Nataf變換和Rosenblatt變換對計算結果的不同影響。Noh等[17]利用Gaussian copula函數求解了RBDO問題。Tang等[18]研究了不同copula函數對兩變量相關模型可靠性分析結果的影響。Jiang等[19]提出了一種基于copula函數的證據理論模型，并構建了相應的結構可靠性分析方法。上述研究為copula函數在結構可靠性中的拓展和應用作出了有價值的探索和嘗試，使相關工作成為近年來結構可靠性分析領域的前沿性和重要性研究方向。然而，這些工作在考慮參數相關性的同時主要是基于一階可靠性方法進行分析的，即將原功能函數進行一階泰勒展開并計算近似可靠性。該處理方式對于很多非線性程度不高的功能函數具有理想的分析精度，但是當功能函數非線性程度較高時，該類方法存在傳統FORM的不足，即可能造成較大的可靠性分析誤差，難以滿足工程需要。為減小一階可靠性方法線性化展開造成的誤差，建立一種基于copula函數的精度更高的高階可靠性分析方法，對于copula函數在結構可靠性領域的更深入拓展以及實際復雜結構適用能力的提升都具有重要的理論意義和工程意義。

本文基于不確定性分析領域近年來發展出的一種處理隨機變量相關性的新型數學模型——vine copula函數[20]，并在筆者現有研究[21]的基礎上提出了一種結構二階可靠性分析方法(vine copula based second order reliability method,VC-SORM)，為存在復雜多維相關性的結構可靠性問題提供了一種高精度的分析方法。

1 vine copula函數基本原理

copula函數可視為一維邊緣分布與多維聯合分布間的連接函數。由Sklar定理[12]，若n維連續隨機向量x=(x1,x2,…,xn)的邊緣分布為F1(x1),F2(x2),…，Fn(xn)，則存在唯一copula函數C，使得

F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))

(1)

其中，F(x1,x2,…，xn)為隨機向量x的聯合概率分布函數。對式(1)求導可得x的概率密度函數：

f(x1,x2,…,xn)=

(2)

其中，fi(xi)為邊緣概率密度函數，c為copula函數C的密度函數：

(3)

目前常用的幾類二維copula函數見表1[13]，表1中θ為copula函數中的相關性參數。這類函數只能較好處地理二維變量間的相關性，但難以完整描述多個變量間的耦合相關關系。

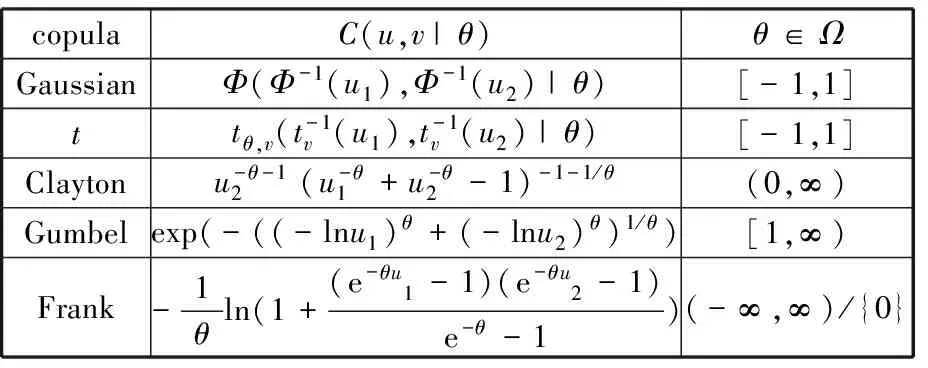
表1 本文所用二維copula函數

對于多維相關性問題，近年來不確定性分析領域出現了一種更為靈活的數學工具——vine copula函數[20,22-24]。vine copula函數的核心思想是通過對多維隨機變量的聯合概率密度函數進行分解，將其轉換為若干個關于原變量或其條件變量的二維copula函數進行處理。對于隨機向量x，按照傳統方法，可通過Rosenblatt變換[14]將其聯合概率密度函數f(x1,x2,…,xn)進行分解：

f(x1,x2,…,xn)=f1(x1)f2|1(x2|x1)·

f3|1,2(x3|x1,x2)…fn|1,2,…,n-1(xn|x1,x2,…,xn-1)

(4)

其中，fk|1,2,…,k-1(xk|x1,x2,…,xk-1)為條件概率密度函數，k=2,3,…,n。對于兩變量情況，由式(2)有：

c12(F1(x1),F2(x2))f2(x2)

(5)

其中，c12為變量x1、x2之間的copula密度函數。對于三變量情況，有

c13|2(F1|2(x1|x2),F3|2(x3|x2))f3|2(x3|x2)=

c13|2(F1|2(x1|x2),F3|2(x3|x2))·

c23(F2(x2),F3(x3))f3(x3)

(6)

F1|2(x1|x2)=C1|2(F1(x1)|F2(x2))=

(7)

F3|2(x3|x2)=C3|2(F3(x3)|F2(x2))=

(8)

由式(6)～式(8)，三維概率密度函數f(x1,x2,x3)可作如下分解：

f(x1,x2,x3)=

f1(x1)f2|1(x2|x1)f3|12(x3|x1,x2)=

f1(x1)f2(x2)f3(x3)c12(F1(x1),F2(x2))·

c23(F2(x2),F3(x3))c13|2(F1|2(x1|x2),F3|2(x3|x2))

(9)

上述分解過程用到了條件分布函數式(7)和式(8)，為表述方便，引入以下h方程來表示二元條件分布：

(10)

ui=Fi(xi) uj=Fj(xj)

對于四維以上概率密度函數，上述分解過程存在多種方式，為方便將多維聯合分布函數分解為二維分布，Bedford等[22-23]引入了一種樹結構圖——vine模型來描述不同的分解方式。常用的vine模型有canonical vine和D-vine，為簡化問題，本文僅考慮D-vine模型。D-vine模型由若干個樹結構組成，對于n維D-vine模型，含n-1層樹結構Tj,j=1,2,…,n-1 ，樹Tj有n-j+1個節點和n-j 條邊，每條邊代表一個二維copula密度函數，例如14|23表示copula密度函數ci,j+1，i=1,2,…,m-1，樹l(2≤l≤m)中的copula函數對為ci,i+l|i+1,i+2,…，j+l-1，i=1,2,…,n-l。一般地，隨機向量x的概率密度函數f(x1,x2,…，xm)對應的D-vine模型如下[24]：

xi+1,xi+2,…,xi+j-1),Fi+j|i+1,i+2,…,i+j-1(xi|

xi+1,xi+2,…,xi+j-1))

(11)

其中，fk(xk)表示隨機變量的邊緣概率密度函數，k=1,2,…,m，下標j表示樹Tj，下標i表示樹Tj中的邊。

2 結構二階可靠性分析方法

假設結構中含n維隨機向量x，其功能函數g為

g(x)=g(x1,x2,…,xn)

(12)

則極限狀態面g(x1,x2,…,xn)=0將變量空間劃分為可靠域ΩR={x|g(x)>0}和失效域ΩF= {x|g(x)≤0}。設x的聯合概率密度函數為f(x1,x2,…，xn)，則結構失效概率Pf可表示為

Pf=∫…∫g(x)≤0f(x1,x2,…,xn)dx1dx2…dxn

(13)

結構可靠度R=1-Pf。而實際工程中，存在著大量的多維相關性問題，即多個隨機變量(超過兩個)之間具有復雜的相互影響關系。文獻[21]針對上述多維相關性問題提出了一階可靠性分析方法(VC-FORM)，對于很多非線性程度不高的功能函數具有理想的精度。在該方法的基礎上，進一步構建一二階可靠性分析方法(VC-SORM)，對于非線性程度較大且存在多維相關性隨機變量的功能函數可靠性問題也能達到理想的精度，從而為復雜結構的可靠性分析提供一種潛在計算工具。

2.1 多維聯合概率密度函數構建

對于多維相關問題，可基于vine copula將多維分布轉換為邊緣分布與多個二維copula函數的乘積，如式(11)所示。各隨機變量的邊緣分布在實際工程問題中通常較易獲得，為此聯合分布函數的建立將最終歸結為多個二維copula函數的構建問題。對于兩變量問題，通常需要基于樣本選擇最優的copula函數來保證相關性分析的精度。下面基于極大似然估計法[25]和AIC準則(Akaike information criterion)[26]對隨機變量的樣本進行統計推斷，從而對變量間的最優copula函數進行選擇并估計相應的相關性參數。

針對隨機向量x中的任一對隨機變量x1、x2，其邊緣累積分布函數分別為F1(x1)、F2(x2)，樣本集為{x1i,x2i}，i=1,2,…,m，其中m為樣本總數。為選擇其最優copula函數，可對任一備選copula函數C，建立似然對數函數如下：

(14)

其中，c為C的密度函數，θ為copula函數中的相關性參數。則θ的估計值可由極大似然估計法求得：

(15)

t copula函數中的自由度v可用同樣方法獲得。對所有備選copula函數進行上述分析，獲得參數θ(和v)后，可用AIC信息準則[26]選擇最優copula函數:

(16)

其中，k為copula函數中參數數目(本文中，對于t copula函數有θ和v有兩個參數，其他copula函數只有θ一個參數)。AIC值越小，則該copula對樣本數據的擬合程度越好。綜上所述，聯合概率密度函數的構建流程如下：

(1)基于vine copula，將聯合概率密度函數分解為若干個二維copula函數及邊緣概率密度函數的乘積。

(2)基于隨機變量的樣本數據，利用MLE方法估計樹1中各備選copula函數的參數，并由AIC準則選出各最優copula函數。

(3)利用h方程將樣本數據轉換為樹2所需數據，并由MLE方法及AIC準則選擇出樹2中的各最優copula函數。

(4)選出樹n-1中的各最優copula函數。

(5)基于式(11)，獲得多維聯合概率密度函數。

2.2 可靠性計算

首先，進行如下等概率變換[8]：

(17)

其中，y=(y1,y2,…,yn)為獨立標準正態向量，Φ為標準正態分布函數。則X空間中的點(x1,x2,…,xn)可通過如下迭代轉換至y空間中的點(y1,y2,…,yn)。

迭代1：

令u1=F1(x1),u2=F2(x2)，…,un=Fn(xn)；

令s1=u1，則y1=Φ-1(s1)；

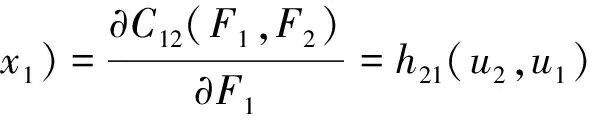
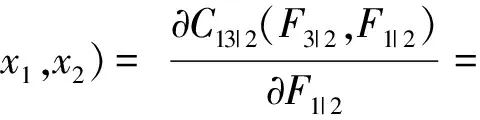
h3|2,1|2(h32(u3,u2),h12(u1,u2))，則s3=Φ-1(r3)；

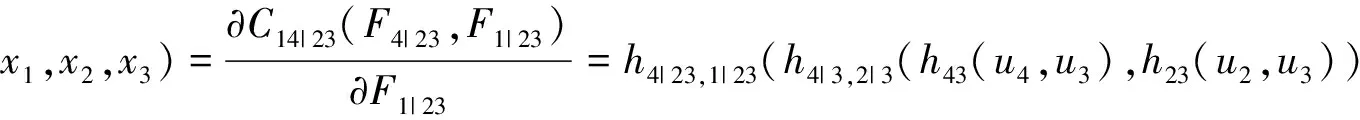
y4=Φ-1(s4)；

…

得到y空間中的點(y1,y2,…,yn)。

在y空間中定義以下一階可靠性指標[1]：

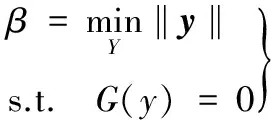
(18)

其中，G表示標準正態空間中的功能函數，最優解y*稱為最可能失效點(most probable point, MPP)，β為可靠度指標。

本文采用改進的HL-RF算法(improved HL-RF algorithm, iHL-RF)搜索MPP，研究結果表明iHL-RF算法在求解式(18)中的優化問題時具有較高的計算效率及穩健的收斂性[27]。iHL-RF由一系列迭代完成，第k迭代步算法可描述為

(19)

yk+1=yk+αdk

(20)

(21)

通過求解以下優化問題確定步長t：

(22)

式中，c為一常數。

,

(23)

采用傳統二階可靠性方法(SORM)的分析思路，在標準正態空間中，對功能函數G(y)在MPP點y*處進行二階泰勒展開：

(24)

其中，α、B、βF為一階可靠性指標。

MPP點處功能函數主曲率為

(25)

其中，bjj為B的對角元素。則式(24)中的功能函數可進一步表示為[28]

(26)

其中，R為二次曲面平均主曲率半徑：

(27)

式(26)對應的二階經驗可靠度指標為[28]

(28)

綜上所述，本文所提出的VC-SORM算法流程如下：

(1)運用D-vine模型將聯合概率密度函數分解為若干個二維copula函數及邊緣概率密度函數的乘積；

(2)由隨機變量的樣本推斷出各最優二維copula函數類型及其相關性參數；

(3)建立多維隨機變量的聯合概率密度函數；

(4)給定初始迭代點x0和迭代步k=0；

(5)用迭代1將隨機向量xk轉換為標準獨立正態向量yk；

(7)令k←k+1,由式(20)得到yk+1；

(8)基于迭代1，反推得到yk+1在原空間上的點xk+1；

(9)如果‖xk+1-xk‖≤ε(ε為容差)，則程序終止，否則轉到步驟(6)；

(10)計算一階可靠度指標βF=‖yk+1‖。

(11)由式(28)計算二階可靠度指標βS和失效概率Pf=Φ(-βS)。

3 算例分析與應用

3.1 算例一

考慮如下功能函數[29]：

(29)

其中，g0為常數；x1服從對數正態分布；x2服從極值Ⅰ型分布；x3服從Weibull分布，其均值和標準差分別為ux1=1，σx1=0.16，ux2=20，σx2=2，ux3=48，σx1=3。

隨機向量x具有500組樣本，其分布如圖1所示。由圖1可知，各變量之間具有較強的相關性，且x2與x3之間具有明顯的下尾部相關性。

采用本文方法對該問題進行分析，即使用vine copula函數將多維概率分布分解為多個二維copula函數，并基于變量樣本對各二維copula函數類型進行最優選擇及參數估計。由樣本可計算出隨機變量之間各備選copula函數的AIC值，見表2。因為AIC越小表示樣本擬合越好，故可知x1與x2，x2與x3，x1|x2與x3|x2對應的最優copula函數類型分別為t copula、Clayton copula、Frank copula，其相應的參數估計值在表2最后兩列中給出。

不同常數g0下，使用本文二次二階矩法(VC-SORM)方法和蒙特卡羅方法(VC-MCS)[21]、一次二階矩法(VC-FORM)[21]三種算法可靠性分析結果見表3。由結果可知，隨著g0的增大，結構的失效概率逐漸增大，同時與蒙特卡羅方法相比，不同常數g0下，本文提出的VC-SORM方法誤差均小于VC-FORM方法誤差。如當g0=0時，VC-FORM方法相對于VC-MCS的誤差為19.35%，而VC-SORM方法相對誤差僅為3.23%。同時也分析了不同的變量相關性對可靠性結果的影響，分析過程中常數g0設置為4。假定二維變量間的Kendall相關系數τ相同，并且沿用上一步分析中的最優copula函數類型，令τ從0.1到0.9變化并使用不同方法進行分析，結果見表4。首先，由結果可發現，在不同的相關系數下本文提出的VC-SORM方法誤差均小于VC-FORM方法誤差。在所有9種情況中，VC-FORM的最大誤差達到56.44%，發生在τ=0.1時；VC-FORM的最大誤差僅為16.59%，發生在τ=0.3時。另外，對于該問題，隨著Kendall相關系數的變大，失效概率整體上也呈現衰減趨勢。如τ=0.9時，VC-MCS方法得到的失效概率為0.001 89，而τ=0.1時失效概率變為0.007 76，后者是前者的4.1倍。這表明，對于該問題，隨機變量相關性對可靠性結果的影響較為顯著，如果單純將其假設為獨立變量進行處理，有可能造成較大的可靠性分析誤差。

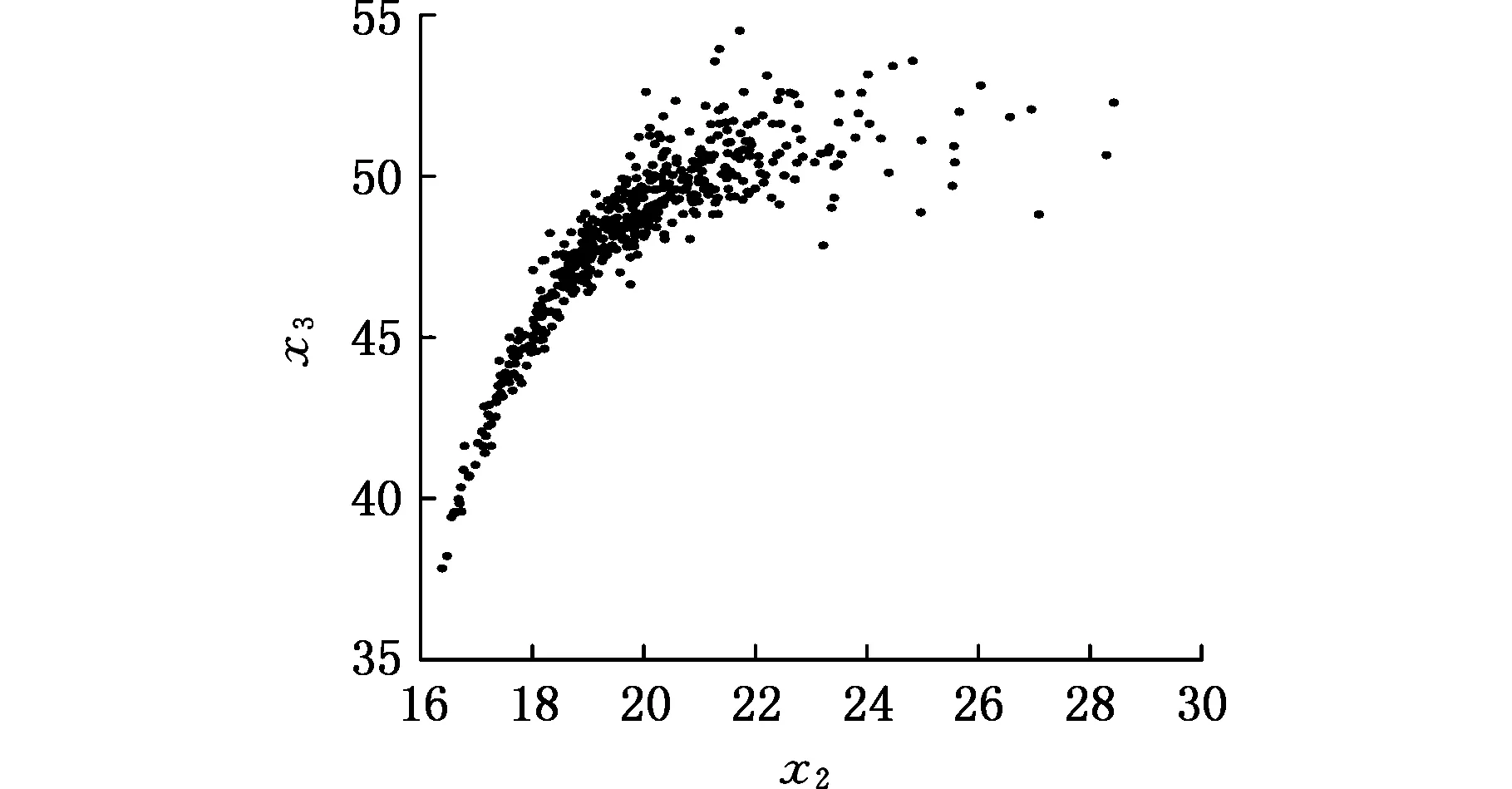
圖1 隨機變量樣本分布圖(算例1)

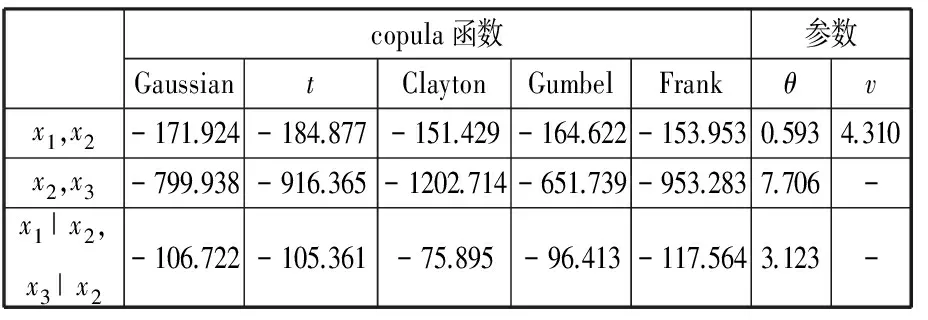
copula函數參數GaussiantClaytonGumbelFrankθvx1，x2-171．924-184．877-151．429-164．622-153．9530．5934．310x2，x3-799．938-916．365-1202．714-651．739-953．2837．706-x1|x2，x3|x2-106．722-105．361-75．895-96．413-117．5643．123-

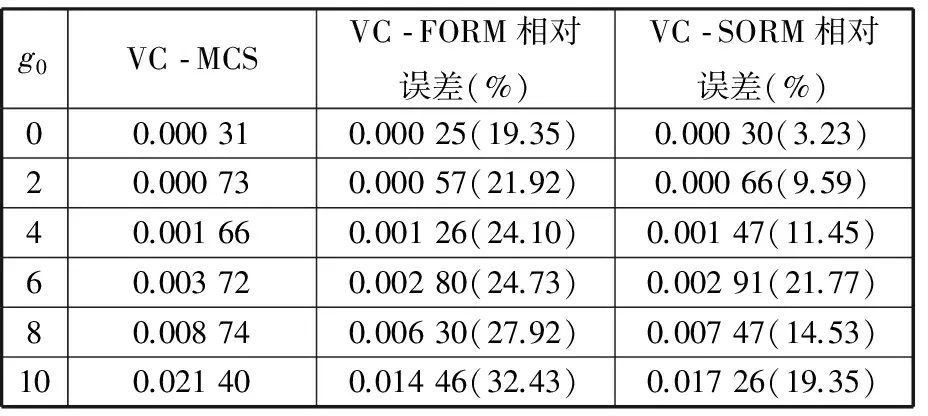
表3 不同g0下的可靠性分析結果(算例1)

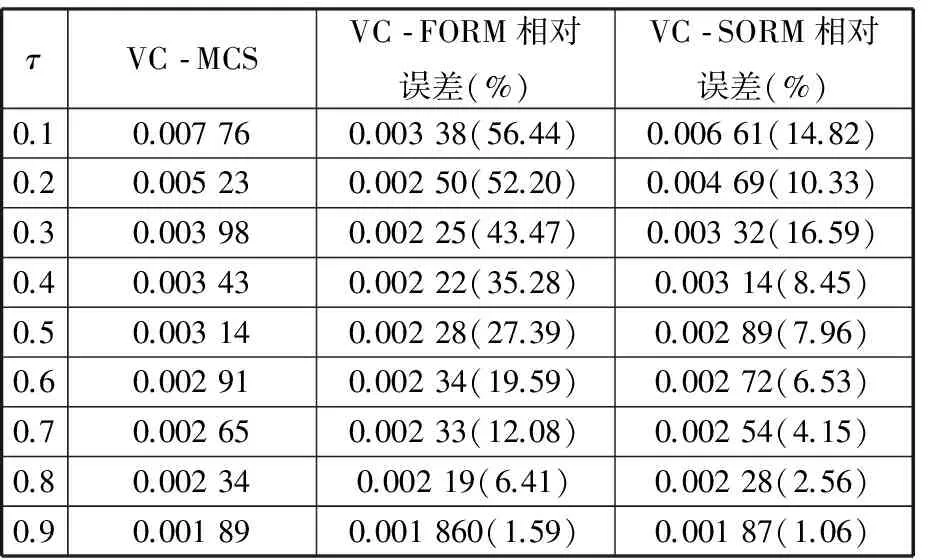
表4 不同相關系數τ下的可靠性分析結果(算例1)

3.2 算例二

近年來，人們對車身耐撞性的設計要求不斷提升。在側碰工況下，B柱最大加速度是衡量車身耐撞性的重要指標。考慮圖2所示的汽車側碰問題，可移動壁障以50 km/h的速度從側面撞向車身。影響車身耐撞性的因素較多，Hou等[30]運用因子篩選法(factor screening method)篩選出圖2所示的4個車身板厚作為關鍵設計變量t=(t1,t2,t3, t4)進行分析。為滿足側碰耐撞性要求，B柱最大加速度a不能超過許可值a0，則可建立以下功能函數：

g(t)=a0-a(t1,t2,t3,t4)

(30)

因為制造誤差t1,t2,t3,t4均為隨機變量，其均值分別為μt1=0.9 mm，μt2=2.1 mm，μt3=1.0 mm，μt4=1.4 mm，變異系數均為0.1，且均服從正態分布。通過實驗設計，運用最優拉丁超立方設計方法在設計空間選取41個樣本點，并調用有限元模型(FEM)進行分析，在此基礎上構建出最大加速度a的響應面函數[30]:

a(t1,t2,t3,t4)=14.5324-0.6917t1+2.4961t2+

0.4466t1t2-0.0473t1t4+0.126t2t3+

0.0621t2t4-0.7866t3t4

(31)

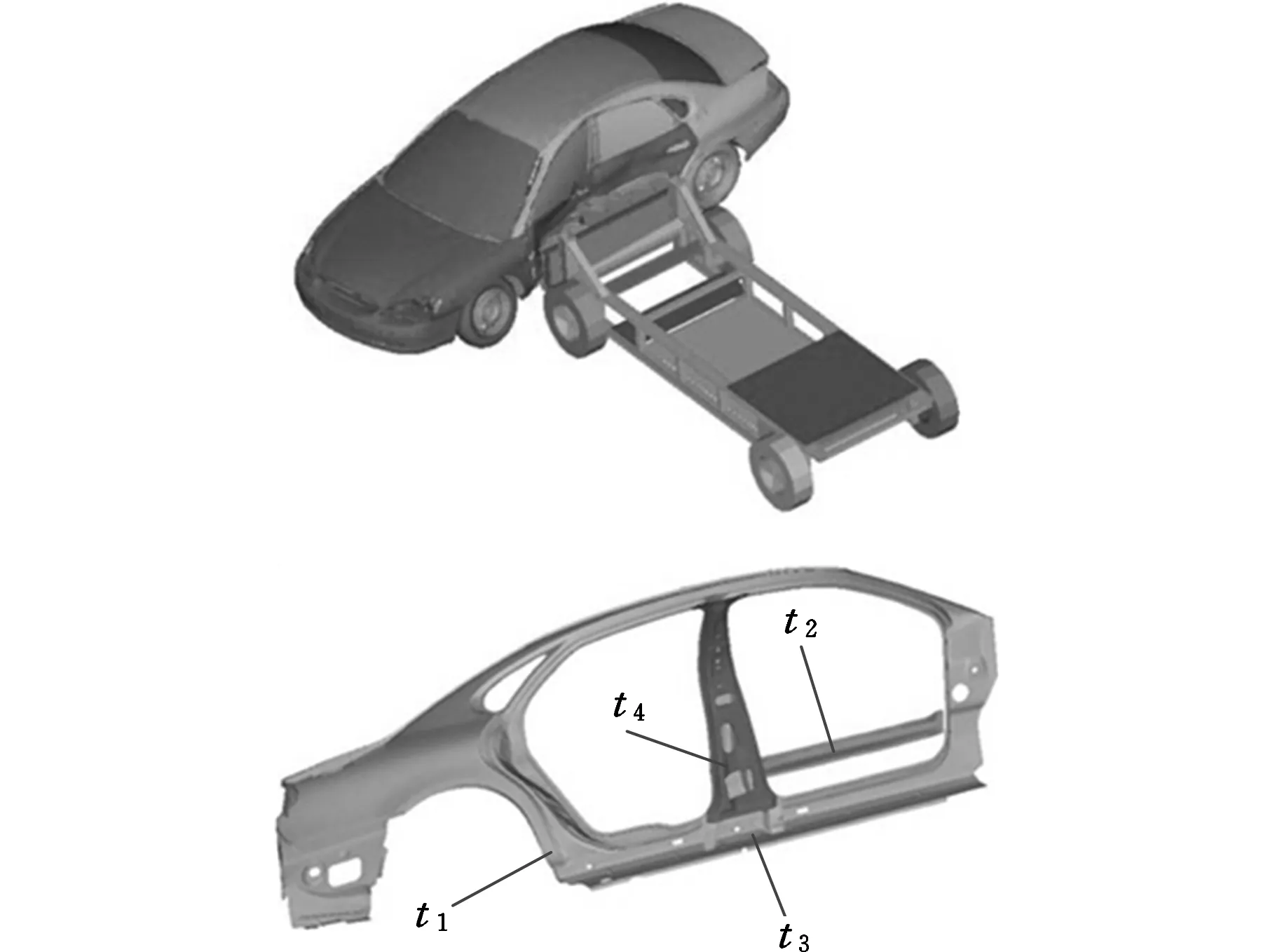
圖2 汽車側碰有限元模型

對4個厚度變量的樣本進行統計推斷，可確定各變量間的最優copula函數類型及相關性參數，見表5。利用本文的VC-SORM方法及現有的VC-MCS、VC-FORM方法分別對上述問題進行可靠性分析，分析過程中調用式(31)中的響應面函數而非原FEM模型，從而大大提高了計算效率，計算結果見表6。由結果可知，當B柱最大侵入量許可值設定為一個較嚴格的指標a0=19.50g時，側碰失效概率超過90%，該情況下車身耐撞性存在較大失效風險，說明該車身結構難以滿足給定的最大加速度設計指標。當a0由19.50g增加到19.90g時，車身側碰失效概率均迅速降低；而當a0達到19.90g時，失效概率已經降低到10-3數量級，說明在該最大加速度的設計指標下車身結構可滿足車身側碰耐撞性的可靠性要求。另外，在不同a0值下，本文提出的VC-SORM算法精度均高于VC-FORM算法精度。當側碰失效概率較大時，VC-FORM和VC-SORM所得失效概率誤差均較小，如當a0=19.50g時，兩種方法的誤差分別僅為2.15%和1.05%；失效概率較小時，VC-SORM方法誤差明顯小于VC-FORM方法誤差，如當a0=19.50g時，VC-FORM方法誤差達到118.21%，而VC-SORM方法誤差僅為16.28%，前者是后者的7.26倍。

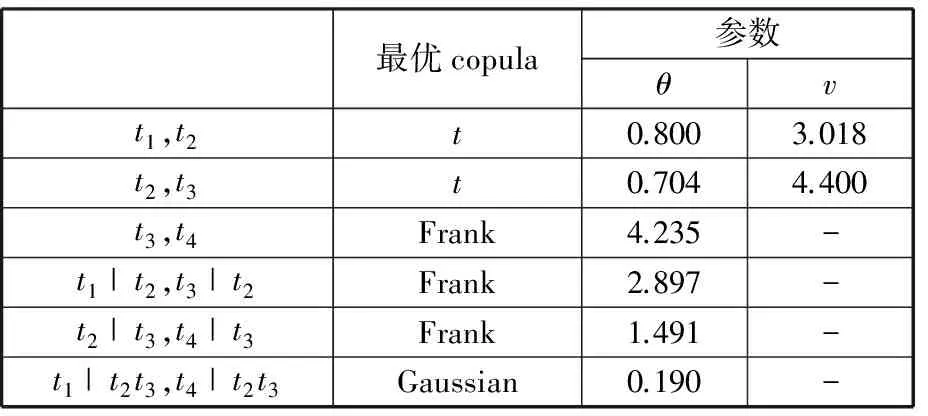
表5 各最優copula函數及參數估計(算例2)

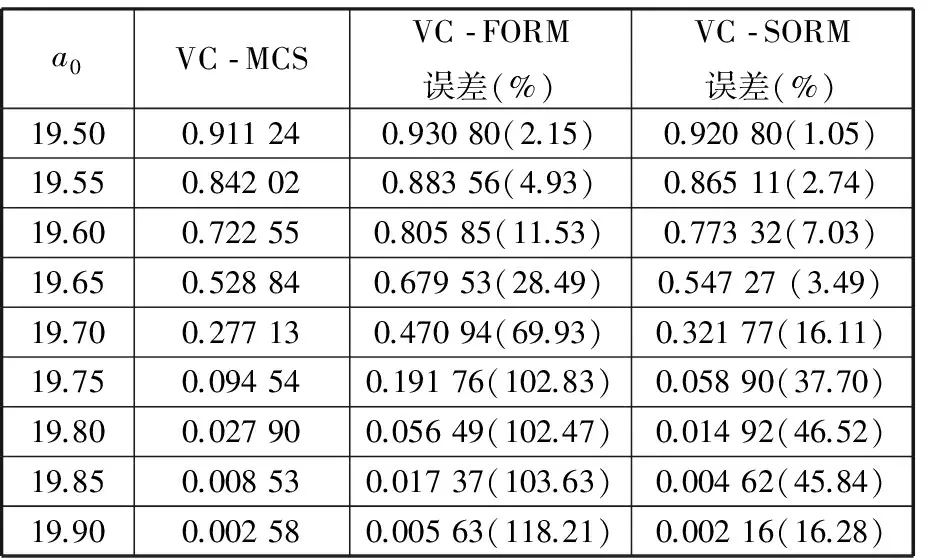
表6 不同a0下的可靠性分析結果(算例2)

4 結語

本文基于vine copula函數，提出了一種處理多維相關性的結構二階可靠性分析方法。基于D-vine模型，可將多維隨機分布轉換為多個二維copula函數的乘積，從而最終轉換為常規的二維copula函數構建問題；進行一階可靠性分析，并在此基礎上對功能函數進行二階近似，獲得精度更高的可靠性分析結果。數值算例分析結果表明：與現有的一階可靠性分析方法VC-FORM方法相比，本文方法具有更高的精度，更適用于處理功能結構函數非線性程度較高的可靠性分析問題。

[1] Hasofer A M, Lind N C. Exact and Invariant Second-moment Code Format[J]. Journal of the Engineering Mechanics Division, 1974, 100(1): 111-121.

[2] Breitung K. Asymptotic Approximations for Multinormal Integrals[J]. Journal of Engineering Mechanics, 1984, 110(3): 357-366.

[3] Thoft-Christensen P, Murotsu Y. Application of Structural Systems Reliability Theory[M]. Verlag: Springer, 1986.

[4] Faravelli L. Response-surface Approach for Reliability Analysis[J]. Journal of Engineering Mechanics, 1989, 115(12): 2763-2781.

[5] Rubinstein R Y,Kroese D P. Simulation and the Monte Carlo Method[M]. New York: John Wiley & Sons, 2011.

[6] Nikolaidis E, Ghiocel D M, Singhal S. Engineering Design Reliability Handbook[M].Boca Raton: CRC Press, 2005.

[7] Liu P L, Der Kiureghian A. Multivariate Distribution Models with Prescribed Marginals and Covariances[J]. Probabilistic Engineering Mechanics, 1986, 1(2): 105-112.

[8] Rosenblatt M. Remarks on a Multivariate Transformation[J]. The Annals of Mathematical Statistics, 1952,23(3): 470-472.

[9] Der Kiureghian A, Liu P L. Structural Reliability under Incomplete Probability Information[J]. Journal of Engineering Mechanics, 1986, 112(1): 85-104.

[10] Li D Q, Wu S B, Zhou C B, et al. Performance of Translation Approach for Modeling Correlated Non-normal Variables[J]. Structural Safety, 2012, 39(4): 52-61.

[11] Lebrun R,Dutfoy A. An Innovating Analysis of the Nataf Transformation from the Copula Viewpoint[J]. Probabilistic Engineering Mechanics, 2009, 24(3): 312-320.

[12] Sklar M. Fonctions de Répartition à N Dimensions Et Leurs Marges[D]. Paris: Université Paris, 1959.

[13] Nelsen R B. AnIntroduction to Copulas[M]. New York: Springer, 1999.

[14] Cherubini U, Luciano E,Vecchiato W. Copula Methods in Finance[M]. New York: John Wiley & Sons, 2004.

[15] Genest C, Favre A C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask[J]. Journal of Hydrologic Engineering, 2007, 12(4): 347-368.

[16] Lebrun R,Dutfoy A. Do Rosenblatt and Nataf Isoprobabilistic Transformations Really Differ[J]. Probabilistic Engineering Mechanics, 2009, 24(4): 577-584.

[17] Noh Y, Choi K K, Du L. Reliability-based Design Optimization of Problems with Correlated Input Variables Using a Gaussian Copula[J]. Structural and Multidisciplinary Optimization, 2009, 38(1): 1-16.

[18] Tang X S, Li D Q, Zhou C B, et al. Impact of Copulas for Modeling Bivariate Distributions on System Reliability[J]. Structural Safety, 2013, 44: 80-90.

[19] Jiang C, Zhang W, Wang B, et al. Structural Reliability Analysis Using a Copula-function-based Evidence Theory Model[J]. Computers & Structures, 2014, 143: 19-31.

[20] Kurowicka D, eds. Dependence Modeling: Vine Copula Handbook[M]. Singapore: World Scientific, 2010.

[21] Jiang C, Zhang W, Han X, et al. A Vine-copula-based Reliability Analysis Method for Structures with Multidimensional Correlation[J]. ASME Journal of Mechanical Design, 2015, 137(6):061405-1-061405-13.[22] Bedford T, Cooke R M. ProbabilityDensity Decomposition for Conditionally Dependent Random Variables Modeled by Vines[J]. Annals of Mathematics and Artificial Intelligence, 2001, 32(1/4): 245-268.

[23] Bedford T, Cooke R M. Vines: a New Graphical Model for Dependent Random Variables[J]. Annals of Statistics, 2002,30(4): 1031-1068.

[24] Aas K, Czado C, Frigessi A, et al. Pair-copula Constructions of Multiple Dependence[J]. Insurance: Mathematics and Economics, 2009, 44(2): 182-198.

[25] Shih J H, Louis T A. Inferences on theAssociation Parameter in Copula Models for Bivariate Survival Data[J]. Biometrics, 1995: 1384-1399.

[26] Akaike H. A New Look at the Statistical Model Identification[J].IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.

[27] Zhang Y,der Kiureghian A. Two Improved Algorithms for Reliability Analysis//Reliability and Optimization of Structural Systems[M]. New York: Springer, 1995.

[28] Zhao Y G, Ono T. NewApproximations for SORM: Part 1[J]. Journal of Engineering Mechanics, 1999, 125(1): 79-85.

[29] 張明. 結構可靠度分析—方法與程序[M]. 北京：科學出版社, 2009.

[30] Hou S, Liu T, Dong D, et al. Factor Screening and Multivariable Crashworthiness Optimization for Vehicle Side Impact by Factorial Design[J]. Structural and Multidisciplinary Optimization,2014,49(1): 147-167.

(編輯 陳 勇)

Second Order Reliability Method of Structures Considering Parametric Correlations

Jiang Chao Deng Qingqing Zhang Wang

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082

A vine copula based second order reliability method(VC-SORM) was proposed to deal with reliability analysis problems with complex multidimensional correlated variables. The multidimensional probability distribution function was converted into two-dimensional copula functions using vine copula function. The maximum likelihood estimation method and the AIC information criterion(Akaike information criterion) were used to identify the optional two-dimensional copulas. Then the joint probability distribution function was built and the first order reliability results were obtained. Based on the first order reliability results, a reliability results with higher accuracy were obtained using the second order approximation. Finally, two numerical examples were provided to verify the effectiveness of the method.

structural reliability; vine copula(VC) function; second order reliability method; parametric correlation

2016-01-04

國家自然科學基金資助項目(51222502,11172096)；湖南省杰出青年基金資助項目(14JJ1016)

TH122

10.3969/j.issn.1004-132X.2016.22.015

姜 潮，男，1978年生。湖南大學汽車車身先進設計制造國家重點實驗室教授。主要研究方向為機械設計及理論、汽車CAE技術。鄧青青，男，1990年生。湖南大學汽車車身先進設計制造國家重點實驗室碩士研究生。張 旺，男,1990年生。湖南大學汽車車身先進設計制造國家重點實驗室碩士研究生。