奈特不確定性下的貝葉斯學習行為模型

周麗莉，段明紅，丁東洋

（南昌大學a.廉政研究中心；b.經濟管理學院，南昌330031）

奈特不確定性下的貝葉斯學習行為模型

周麗莉a,b，段明紅b，丁東洋a

（南昌大學a.廉政研究中心；b.經濟管理學院，南昌330031）

奈特不確定性和風險下的決策框架差異明顯，傳統風險度量模型在處理不確定性問題上表現的并不令人滿意。處理奈特不確定性的主要統計決策方法可分為新古典方法、參數修正方法和貝葉斯方法。在貝葉斯框架下，可以基于學習行為構造一個融合外部環境信息和內生主觀預期的模型，將期望效用最高的行為視為最優決策。貝葉斯學習行為模型在實踐中能夠有效的區分風險和不確定性，對于解決不確定性環境下傳統風險度量模型容易低估風險和忽略極端風險的問題具有積極意義。

奈特不確定性；風險；貝葉斯方法；學習行為

0　引言

奈特不確定性和風險下決策框架差異的提出可以追溯到20世紀初，弗蘭克·奈特和約翰·梅納德·凱恩斯分別在20年代和30年代獨立提出了二者的差別以及相應的經濟后果，至今對統計決策問題的分析仍然至關重要。在風險狀態下，決策者能夠給出經濟后果的概率分布，例如汽車制造商通過大量重復的實驗，能夠估計出汽車行駛一定里程后，在不同環境下制動失靈的概率。相比而言，在不確定性條件下概率是不可獲得的，因為沒有足夠相似的事件匯總推斷相應的頻率。簡單的說，區分風險和不確定性的關鍵在于，依據過去觀測頻率能否可靠的推斷未來發生的事件，如果可以，那么決策的環境中僅存在風險，如果不可以，那么就存在奈特不確定性(在沒有歧義的情況下簡稱為不確定性)[1]。

近年來奈特不確定性下的風險管理和決策問題越來越引人關注，一個主要動機是由于觀測到的行為結果與模型的預測結果存在偏差。首先，為較少發生而影響巨大的事件指定概率是非常困難的，例如很少有先例的金融危機。這意味著在理解這些進程發展的過程中，對事件發生似然性的評估將隨之改變，有時甚至是大幅度的變化；其次，對于初始條件和外界擾動的變化，決策行為是非常敏感的。復雜系統具有一個臨界點，參數值的微小改變可能導致系統從一個穩定狀態進入到恐慌的蔓延狀態。因而現代全球市場的相互關聯的性質使風險通過系統中難以預料的方式表現出傳播迅速而且廣泛的特征。

針對市場上的不確定性，考慮到決策行為的復雜性，大量研究認同市場參與者的行為受到信念影響，需要綜合過去、現在和未來的信息作出決策[2]。驅動決策系統的變量與人們的認知密切相關，市場參與者對于經濟形勢的不確定性，使其表現出更加保守的風險承擔行為，這反過來進一步削弱經濟發展的勢頭。這種信念將隨外部環境的變化而不斷調整，與之相伴隨的就是學習行為[3]。

近年來國內學術領域也十分關注奈特不確定性下的行為決策研究，一些的學者結合中國市場環境，基于學習行為和信念變化研究投資動態、消費特征以及資產價格的異常現象[4]。特別是最近的研究中，龔樸和高原(2010)[5]通過將市場學習行為引入信用風險結構模型，建立內生的動態均衡模型，描述投資者隨著學習過程改變的信念對財富轉移的影響，并指出投資者的樂觀信念無法持續將誘發危機的可能；俞紅海、陸蓉和徐龍炳(2014)[6]基于市場學習行為構建模型，發現管理者迎合并利用了投資者對價格的信念幻覺增加資金流入，明確了監管過程中考察學習行為的重要性。雖然這些分析框架并不能完全等同于不確定性下的真實決策，但是已經是對標準風險模型的重大改進，并直接為風險管理提供有效的指導。

1　奈特不確定性下的行為決策方法

1.1傳統處理方法

從奈特不確定性提出至今，雖然奧地利經濟學派以及諸如Shackle(1955)、Ellsberg(1961)和Malinvaud(1973)等著名思想家不斷豐富其內涵，但是實際上奈特不確定性在主流經濟學中被錯位的現象更為普遍。較有代表性的是著名經濟學家Tobin(1959)直接將奈特不確定性等同于可量化的風險，基于這種思想，隨后一些新興的金融學家在假定理性預期和有效市場的情況下，僅考察市場上的風險對決策的影響[7]。此外，作為考利斯委員會的一員，可以說Arrow(1951)的觀點也代表著當時考利斯委員會對不確定性的態度。他批判了那些想要清晰解釋不確定性與風險之間概念差別的嘗試，認為人們可以假定主觀概率的存在，回避奈特不確定性的問題。

與Arrow(1951)同時期的Alchian(1950)則認為行為決策確定標準的缺乏與確定性下行為理論的利益最大化是一致的，也就是說本質上應該將不確定性下的行為視為隨機的。Alchian(1950)處理不確定性的方法主要有三個關鍵步驟：一是在正式的決策框架中引入不確定性，二是將奈特不確定性的本質視為不可測性的實例，最后將不可測性視為隨機過程。這種處理方法是復雜且抽象的，但是意義深遠：第一通過將不可測性代替奈特不確定性，實際上是將其視為一種可以融入模型的因素，進而可以使用一些數學方法（如蒙特卡洛模擬、鞅方法等）來處理數據，從而使得不確定性可以在決策框架中被考慮；第二，決策框架在Alchian(1950)的“實證檢驗”中被證明是可行的；第三，為經濟決策相關的分析框架提供了更加廣義的研究思路。基于Alchian(1950)的基本思想，數學方法中諸如伊藤引理(Ito's Lemma)或半鞅(Semi-martingales)方法被逐漸融入金融理論。

1.2行為決策方法的分流

從20世紀80年代開始，大量的文獻開始關注奈特不確定性下的行為決策研究。在比較重要的文獻中，Gilboa and Schmeidler(1989)和Bewley(1986)指出奈特不確定性的概念等同于貝葉斯信念的缺乏；Gilboa and Schmeidler (1989)假定參與人是模糊厭惡者，根據先驗集合采用最大最小準則作出謹慎決策。實際上，這些處理方法都是將靜態埃爾斯伯格實驗(Ellsberg,1961)中行為表現作為不確定性的主要形式。在隨后的研究中[8]人們逐漸發現傳統風險度量模型的預期結果難以充分解釋代理人的行為決策，這使得研究奈特不確定性下行為決策的方法有所分流，主要包括三類：

第一類為新古典方法，將期望效用理論和新古典假設作為評價決策行為的標準。在這類研究方法中，大量的文獻對投資決策等問題進行了探討，繼續沿用傳統的風險度量方法，決策行為如果出現與新古典范式的偏離，則被視為次優的或非理性的行為[9]。

第二類為修正參數方法，將行為的偏離采用增加參數方式修正。例如，Kahneman and Tversky(1979)的前景理論通過增加額外的參數和概率轉化方法完善傳統的期望效用框架；Epstein andWang(1994)在奈特不確定性下建立了盧卡斯純交換均衡模型，將不確定性作為溢價因子進行資產定價；Chen and Epstein(2002)在連續時間狀態下求解奈特不確定性下的消費決策問題。類似的方法讓我們認識到了獲取信息的高額成本以及非標準偏好的心理原因。但是基本分析框架仍是在風險狀態下的最優決策，而非直接面對不確定性。一些研究[10]也指出忽略或簡化信息下的決策不能被認為是最優的。

第三類為貝葉斯方法，基于貝葉斯學習法則給出決策。很多分析人員把貝葉斯方法看作決策中處理不確定性的有效途徑。實際上在更為早期的文獻中就將信念與決策聯系起來，如Simon(1955)通過引入“有限理性”將心理變化與決策行為聯系起來。Matthew(1999年獲得克拉克獎)以及Kahneman and Smith(2002年獲得諾貝爾經濟學獎)都認為決策主體在有意識的識別并解釋外部信息的過程中進行決策，也就是在有限的時間、知識和其他資源條件下，基于學習過程分析環境特征給出決策[11]。

對于奈特不確定性下的行為決策研究，我們認為應該遵循Knight(1921)的基本觀點，即“參與者總會做出行為決策，即使他們使用的是主觀概率”。實際上Keynes(1937)也做出類似的陳述，“雖然存在不確定性，但是參與者不得不做出決定并且付諸行動”。凱恩斯和奈特的觀點比現代主觀預期效用理論早了幾十年，與當前不確定性經濟學的基本理論一致，即在存在不確定性時的決策行為與貝葉斯統計決策理論密切相關[12]。

2　貝葉斯學習行為模型

2.1貝葉斯學習法則

奈特不確定性下的風險度量問題有三個重要特征：一是決策變量缺少經驗數據；二是采納專家觀點進行決策非常必要；三是需要同時考慮參數不確定性和模型不確定性。貝葉斯統計決策理論重點關注概率模型中與參數相關的不確定性，有效利用專家觀點等主觀信息，從而能夠反映出可替換模型的表現質量，因而在處理奈特不確定性下的風險度量問題時具有一定的優勢。

貝葉斯統計決策方法在識別事件所有可能狀態的基礎上，通過界定狀態中的外生變量和行為反應參數，對每個狀態指定相應的主觀概率，而每個狀態與決策行為的結合都將形成對應的結果。在貝葉斯框架下，原則上要求能夠運用指定的主觀概率對潛在行為計算期望效用，通過學習行為構造一個融合外部環境信息和內生主觀預期的模型，將期望效用最高的行為視為最優決策。學習的基石是貝葉斯法則，即代理人在獲取新的信息后將更新他們的信念。假定代理人對參數θ存在不確定性，在沒有觀測到任何信號時，關于θ的先驗是均值為θ0，方差為σ02的正態分布。當觀測到θ的T個獨立信號時，令st=θ+εt，其中εt是均值為0方差已知σ2的正態變量。根據貝葉斯法則，θ的后驗分布也是正態的，其期望值和方差分別為：

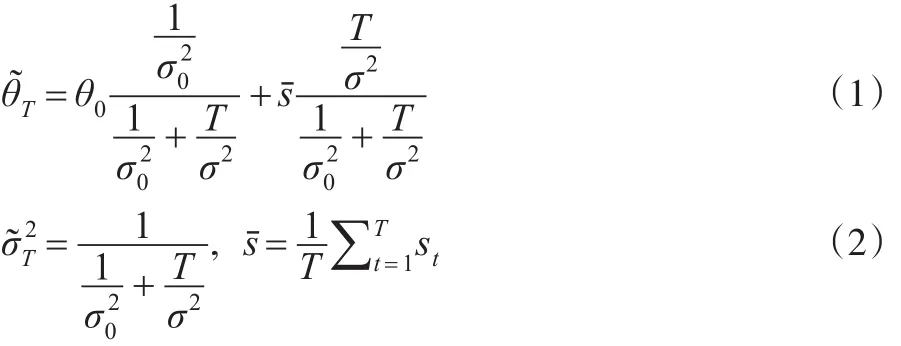
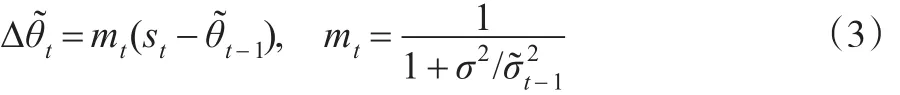
如果觀測序列是連續而非離散的情形，觀測信號采用差分形式表示，dst=θdt+σdWt，其中dWt表示布朗運動。更新公式表示為：

2.2貝葉斯學習模型的作用

下面以一個簡單的模型說明貝葉斯學習行為模型在不確定性下進行行為決策的作用。假定市場上包括n項期望收益率為ri的風險資產和一項收益率為rf的無風險資產組成。以金融市場上的銀行為例，令向量r表示n項資產的預期收益率，1表示n維單位向量，有如下等式：

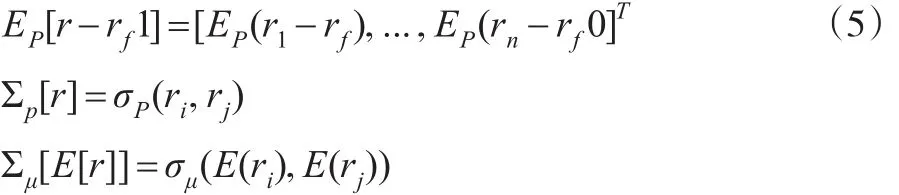
其中i，j=1，2，...n，Σp[r]和Σμ[E[r]]分別表示在參考概率P和先驗分布μ下收益和期望收益的方差協方差矩陣。EP[r-rf1]表示在參考概率P下的預期超額收益。假定決策者可以通過經過學習過程獲取式（5）中的相關信息，那么在貝葉斯更新后銀行最優資產組合的解可表示為：

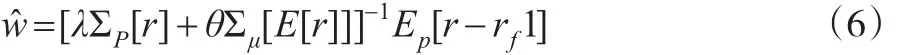
其中λ和θ分別表示了對待風險和不確定性的態度。從最優解的表達式可以發現，沒有不確定性時Σμ[E[r]]=0，或者銀行對不確定性的態度中性時θ=0，此時馬科維茨-托賓風險模型能夠準確的預測銀行最優資產組合。然而事實上銀行總是表現為不確定性規避的態度，隨著不確定性的上升，收益相關性趨近于1，θΣμ[E[r]]為正，導致風險模型失效。更重要的是，式（6）中最優資產組合的權重將低于風險狀態下的權重。可見，當銀行配置資產時忽略了不確定性，將使其資產組合承擔更多的風險。

如果需要描述不確定性下銀行資產配置的決策行為，可以采用貝葉斯學習模型。令隨機過程κ服從傳統的區制轉換馬爾科夫過程，κ有兩種可能，分別對應信貸環境較好的狀態κh和信貸環境較差的狀態κl。馬爾科夫過程具有連續的轉移概率，以及對應的轉換概率從而這一階段的學習主要表現為對轉移概率給出的信念，信念是基于初始先驗與κ在不同階段的觀測值綜合形成的。經過充分的觀測獲取了關于κh和κl足夠的數據組合，銀行將學習到κ真實的區制轉移概率。

具體的學習過程在基于初始信念的基礎上可以采用概率模型描述（如beta-binomial模型）。令κ的歷史觀察值κT={κ0，κ1，...κT-1，κT，}，初始先驗的分布在t=0時表示為p(Fs)。基于beta-binomial概率模型，通過貝葉斯學習得到后驗序列銀行的初始信念應該包括κ的可能值{κh，κl}，也就是說對一種特定狀態的持續時間和一種狀態轉移到另一種狀態的次數要有信念。表示從狀態κi轉移到κj的次數，那么銀行的信念可表示為這些數據和先驗，在beta-binomial概率分布基礎上共同構成了學習過程。如初始先驗表示為，那么可以給出假定先驗是獨立的[13]，而且決定因素是，即在時間t之前給出關于轉移數量的信念。的后驗分布分別表示為：而且后驗均值滿足：

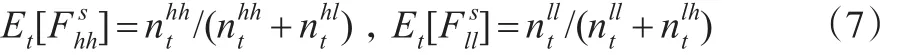
掌握了后驗均值的變動也就意味著描述出了不確定性下決策行為的變化過程。

3　結語

在實踐中，面對復雜的市場和不確定性，監管者必須在決策時考慮市場學習行為。近期的研究[14,15]都認為在貝葉斯框架下建立學習模型能夠有效的區分風險和不確定性，本文的觀點也將對面臨不確定性的風險度量提供新的研究思路和方法，值得引起風險分析人員的關注。需要說明的是貝葉斯學習行為模型的有效性與風險可測性和風險源的可分解性密切相關。圖1中第一個維度以縱軸表示風險可測性，沿縱軸方向從下至上表示從風險無法度量的根本不確定性到風險能夠可靠的量化。越接近原點，不確定性程度越高；越遠離原點，金融市場越來越像人壽和財產保險市場一樣具有豐富的信息和穩定的參數，風險能夠被可靠的度量。第二個維度用橫軸表示風險源的可分解性。可分解性與市場環境的復雜程度密切相關，低分解性意味著風險組成部分不易被拆分以單獨分析，高分解性意味著風險能夠被有效的量化分析。

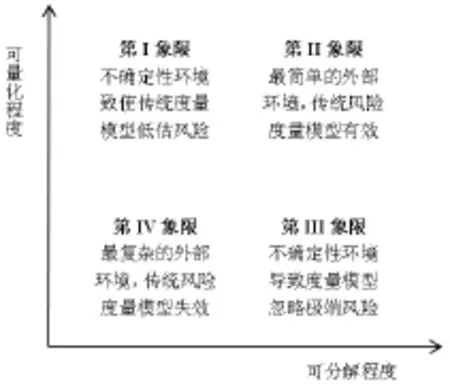
圖1　不確定性下的風險度量模型

將風險可測性和風險源的可分解性這兩個維度結合起來，可以說明風險度量模型的有效性。當我們可以依據過去的觀測值推斷分布，而且能夠將系統分解成小的組成單位，可分析風險如何在單位內部和單位之間轉移，這時風險度量模型是最有效的，稱之為第II象限。當風險可以量化，但金融環境高度復雜，風險度量過程中面臨模型不確定性問題，稱之為第I象限。當風險源可分解程度較高，但是模型參數面臨不確定性，風險度量模型難以預測低概率高影響的極端事件，稱之為第III象限。但是在第IV象限，風險源的低分解性和低風險可測性并存，導致風險度量模型失效。因而貝葉斯學習行為模型主要適用于第II和第III象限的環境，可用于解決傳統度量模型低估風險及容易忽略極端風險的問題。

[1]丁東洋,周麗莉.貨幣政策風險與不確定性的統計學分析[J].統計與決策,2009，(9).

[2]Freixas X,Laeven L,Peydro JL.Systemic Risk,Crises,and Macro?prudentialRegulation[M].Cambridge:MITPress,2015.

[3]Cogley T,Sargent T.Anticipated Utility and Rational Expectations as Approximations of Bayesian Decision Making[J].International Eco?nomic Review,2008,49(1).

[4]陸靜,曹國華,唐小我.基于異質信念和賣空限制的分割市場股票定價[J].管理科學學報,2011,14(1).

[5]龔樸,高原.非理性預期對信用衍生產品定價的影響—美國次貸危機的啟示[J].管理科學學報,2010,13(9).

[6]俞紅海，陸蓉，徐龍炳.投資者名義價格幻覺與管理者迎合[J].經濟研究，2014，(5).

[7]Rosser J.Alternative Keynesian and Post Keynesian Perspectives on Uncertainty and Expectations[J].Journal of Post Keynesian Econom?ics,2001,23(4).

[8]Guy T,Karny M,Wolpert D.Decision Making:Uncertainty,Imperfec?tion,Deliberation and Scalability[M].Switzerland:Springer Interna?tional Publishing AG，2015.

[9]Easley D,O'Hara M.Liquidity and Valuation in an Uncertain World [J].Journalof Financial Economics,2010,91(1).

[10]Brunnermeier K,Sannikov Y.A Macroeconomic ModelWith a Fi?nancial Sector[J].American Economic Review,2014,104(2).

[11]Christiano J,Motto R,Rostagno M.Risk Shocks[J].American Eco?nomic Review,2014,104(2).

[12]Blanchard O,Romer D,Spence M,et al.In theWake of the Crisis: Leading Economists Reassess Economic Policy[M].Cambridge:MIT Press,2014.

[13]Bachmann R,Elstner S,Sims E.Uncertainty and Economic Activity: Evidence From Business Survey Data[J].Macroeconomics,2013,5 (2).

[14]Weitzman M.Subjective Expectations and Asset-return Puzzles[J]. American Economic Review,2007,97(4).

[15]Ilut C,Schneider M.Ambiguous Business Cycles[J].American Eco?nomic Review,2014,104(8).

（責任編輯/易永生）

0212.8：C934

A

1002-6487（2016）19-0016-04

國家自然科學基金青年項目(71401069)；教育部人文社科研究青年基金項目（15YJC630194）；全國統計科學研究計劃項目(2013LY001)；江西省高校人文社會科學重點研究基地項目(JD1412)

周麗莉（1980—），女，江西臨川人，博士，副教授，研究方向：國際金融市場與風險管理方法。段明紅（1990—），男，江西余干人，碩士研究生，研究方向：風險度量。丁東洋（1979—），男，遼寧撫順人，博士，副教授，研究方向：貝葉斯數據分析方法與風險管理技術。