縱向數(shù)據(jù)下部分非線性模型的廣義經(jīng)驗(yàn)似然推斷

肖燕婷,孫曉青,孫瑾

(西安理工大學(xué)理學(xué)院應(yīng)用數(shù)學(xué)系,陜西西安710054)

縱向數(shù)據(jù)下部分非線性模型的廣義經(jīng)驗(yàn)似然推斷

肖燕婷,孫曉青,孫瑾

(西安理工大學(xué)理學(xué)院應(yīng)用數(shù)學(xué)系,陜西西安710054)

本文研究了縱向數(shù)據(jù)下部分非線性模型中未知參數(shù)的置信域的構(gòu)造.利用經(jīng)驗(yàn)似然方法,構(gòu)造了非線性函數(shù)中未知參數(shù)的廣義對(duì)數(shù)經(jīng)驗(yàn)似然比統(tǒng)計(jì)量,證明了其漸近于卡方分布.同時(shí),得到了未知參數(shù)的最大經(jīng)驗(yàn)似然估計(jì),并證明了其漸近正態(tài)性.

縱向數(shù)據(jù);部分非線模型;經(jīng)驗(yàn)似然;置信域

1　引言

縱向數(shù)據(jù)是生物醫(yī)學(xué)、流行病學(xué)和計(jì)量經(jīng)濟(jì)學(xué)等學(xué)科中經(jīng)常出現(xiàn)的一類復(fù)雜數(shù)據(jù).由于其具有個(gè)體間觀測(cè)值獨(dú)立,個(gè)體內(nèi)觀測(cè)值相關(guān)的特性,不同于一般的獨(dú)立數(shù)據(jù),對(duì)其相關(guān)研究已成為統(tǒng)計(jì)學(xué)界的研究熱點(diǎn)之一.

本文考慮如下的縱向數(shù)據(jù)下的部分非線性模型

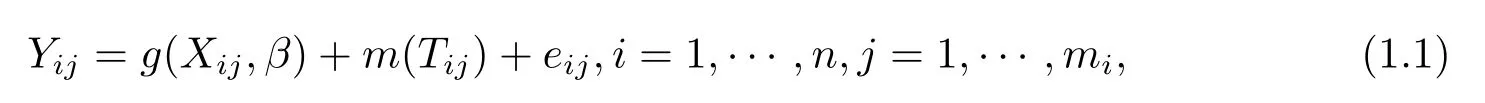
其中觀測(cè)數(shù)據(jù)來(lái)自n個(gè)個(gè)體,第i個(gè)個(gè)體具有mi次觀測(cè),總的觀測(cè)次數(shù)為和(Xij∈Rp,Tij)分別為第i個(gè)個(gè)體的第j(j=1,···,mi)次觀測(cè)的響應(yīng)變量和協(xié)變量;β為d×1維未知參數(shù)向量;g(.,.)為已知的可測(cè)函數(shù);m(.)為定義在[0,1]上的未知光滑函數(shù); eij為隨機(jī)誤差.記第i個(gè)個(gè)體的隨機(jī)誤差向量為ei=(ei1,ei2,···,eimi)T,{ei,i=1,···,n}相互獨(dú)立,且E(ei)=0,Var(ei)=Σi并要求Σi為正定陣.

如果不考慮縱向數(shù)據(jù),部分非線性模型(1.1)在獨(dú)立數(shù)據(jù)下,已有不少學(xué)者研究了模型中未知參數(shù)和未知函數(shù)的估計(jì),如Li和Nie[1]提出可以采用輪廓非線性最小二乘方法和局部線性逼近技術(shù)估計(jì)模型參數(shù);Xiao等[2]將經(jīng)驗(yàn)似然方法應(yīng)用于該模型,構(gòu)造了未知參數(shù)和未知函數(shù)的經(jīng)驗(yàn)對(duì)數(shù)似然比統(tǒng)計(jì)量,從而可以得到未知參數(shù)的置信域和未知函數(shù)的同時(shí)置信帶.

對(duì)于復(fù)雜數(shù)據(jù)下的部分非線性模型,馮三營(yíng)等[3]考慮了當(dāng)非參數(shù)協(xié)變量具有可加測(cè)量誤差時(shí),采用逆卷積方法,構(gòu)造了模型中未知參數(shù)的經(jīng)驗(yàn)對(duì)數(shù)似然比統(tǒng)計(jì)量,并證明了其具有漸近卡方分布.接著,文獻(xiàn)[4]給出了模型中回歸系數(shù),光滑函數(shù)以及誤差方差的最大經(jīng)驗(yàn)似然估計(jì).肖燕婷等[5]借助核實(shí)數(shù)據(jù),給出了協(xié)變量帶測(cè)量誤差的部分非線性模型中未知參數(shù)的兩種估計(jì)方法.武大勇等[6]在響應(yīng)變量隨機(jī)缺失的情形下,給出了未知參數(shù)的最大經(jīng)驗(yàn)似然估計(jì),并證明了估計(jì)的漸近正態(tài)性.劉強(qiáng)[7]在解釋變量帶有測(cè)量誤差且響應(yīng)變量隨機(jī)缺失的復(fù)雜情形下,利用核實(shí)數(shù)據(jù),給出了未知參數(shù)和非參數(shù)函數(shù)的兩種估計(jì).但在縱向數(shù)據(jù)下,對(duì)該模型的研究還比較少.

本文針對(duì)縱向數(shù)據(jù)下的部分非線性模型(1.1),利用Owen[8]等提出的經(jīng)驗(yàn)似然方法,構(gòu)造了模型中未知參數(shù)β的廣義對(duì)數(shù)經(jīng)驗(yàn)似然比統(tǒng)計(jì)量,證明了所提統(tǒng)計(jì)量的漸近χ2分布,所得結(jié)果可以構(gòu)造未知參數(shù)的置信域.同時(shí),利用對(duì)數(shù)經(jīng)驗(yàn)似然比函數(shù),得到了未知參數(shù)的最大經(jīng)驗(yàn)似然估計(jì),證明了其漸近正態(tài)性.

2　方法與主要結(jié)果

假設(shè)觀測(cè)數(shù)據(jù){(Xij,Tij,Yij),i=1,···,n,j=1,···,mi}由模型(1.1)產(chǎn)生.對(duì)(1.1)式兩邊在給定Tij=t時(shí)求條件期望,可以得到

其中m1(t,β)=E(g(Xij,β)|Tij=t),m2(t)=E(Yij|Tij=t).利用核估計(jì)方法,可以得到m1(t,β)和m2(t)的估計(jì),分別由下式給出

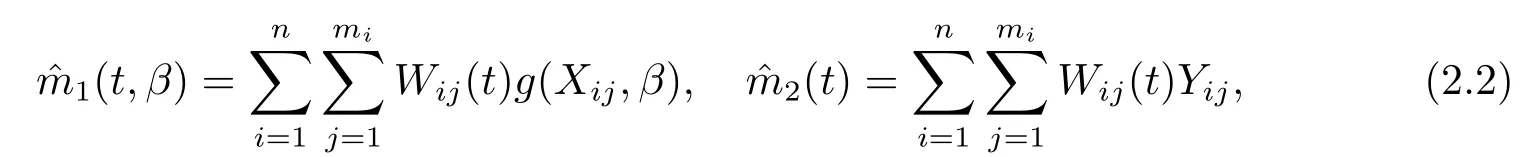
其中Wij(t)=Kh(Tkl-t)為核權(quán)函數(shù),Kh(.)=K(./h)且K(.)為核函數(shù),h為帶寬.因此m(t)的估計(jì)為

為了構(gòu)造未知參數(shù)β的對(duì)數(shù)經(jīng)驗(yàn)似然比函數(shù),需要引入如下的輔助隨機(jī)向量

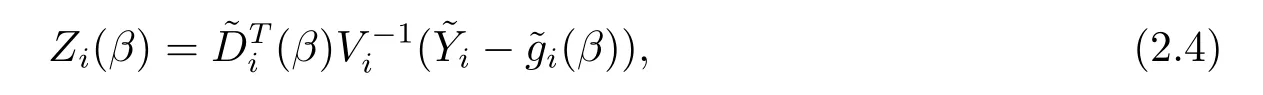
其中Vi可以為任意指定的工作協(xié)方差陣.但在實(shí)際應(yīng)用中,為了避免由于錯(cuò)誤指定協(xié)方差陣而引起的估計(jì)效率的降低,可以用其估計(jì)值代替真實(shí)值Vi,且,其中Zi(β)=0,且在Zi(β)中令Vi=I得到的未知參數(shù)β的初估計(jì).

類似于文獻(xiàn)[9],定義如下廣義的經(jīng)驗(yàn)對(duì)數(shù)似然比函數(shù)

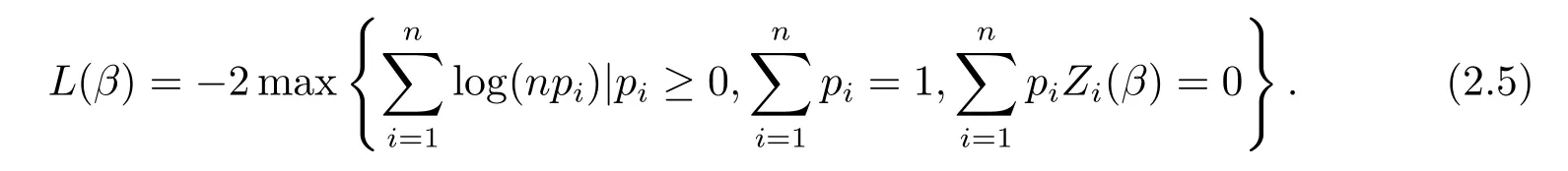
根據(jù)Lagrange乘子方法,L(β)可以寫成

其中λ=λ(β)由下式?jīng)Q定

通過(guò)極小化L(β),可以得到參數(shù)β的最大經(jīng)驗(yàn)似然估計(jì),記做.將代入(2.3)式,可以得到未知函數(shù)m(t)的最終估計(jì),為(t)=2(t)-1(t,).

3　漸近性質(zhì)

令g(1)(Xij,β)=h(Tij,β)+uij(β),i=1,···,n,j=1,···,mi,其中h(Tij,β)= E(g(1)(Xij,β)|Tij),且E(uij(β))=0.令ha(Tij,β)為h(Tij,β)的第a個(gè)分量,a=1,···,d.類似于(2.2)式,ha(t,β)的核估計(jì)可以定義為a(t,β)=其中(Xij,β)為g(1)(Xij,β)的第a個(gè)分量.

為了得到估計(jì)量的漸近性質(zhì),需要給出以下假設(shè)條件.

C1:帶寬滿足h=h0N-1/5,對(duì)某個(gè)h0＞0.

C2:核函數(shù)K(.)為對(duì)稱的概率密度函數(shù),且在它的支撐[-1,1]上有界.

C4:T的密度函數(shù)f(t)在(0,1)是連續(xù)可微的,且有界.

C5:對(duì)任意的β,非線性函數(shù)g(x,β)具有二階連續(xù)導(dǎo)數(shù).

C6:函數(shù)m(t),ha(t,β),a=1,···,d在(0,1)上是二次連續(xù)可微的.

C7:定理2.2中的矩陣Γ為正定矩陣.

注條件C1-C7是文獻(xiàn)中經(jīng)常用到的條件.條件C1說(shuō)明了在估計(jì)m(.)時(shí)不必欠光滑; C2為核函數(shù)的一般性條件;條件C3-C6為部分非線性模型中常見的條件;條件C7保證了最大經(jīng)驗(yàn)似然估計(jì)的漸近方差的存在.

定理2.1假設(shè)條件C1-C6成立,如果β為真實(shí)參數(shù)值,則有

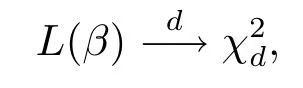
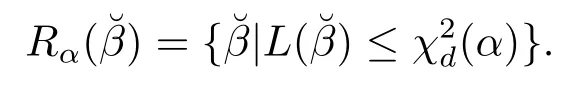
定理2.2假設(shè)條件C1-C7成立,則有

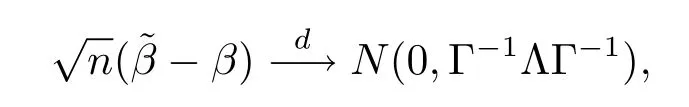
4　定理的證明

為了完成定理的證明,需要首先給出以下引理.

引理1假設(shè)條件C1-C6成立,則有

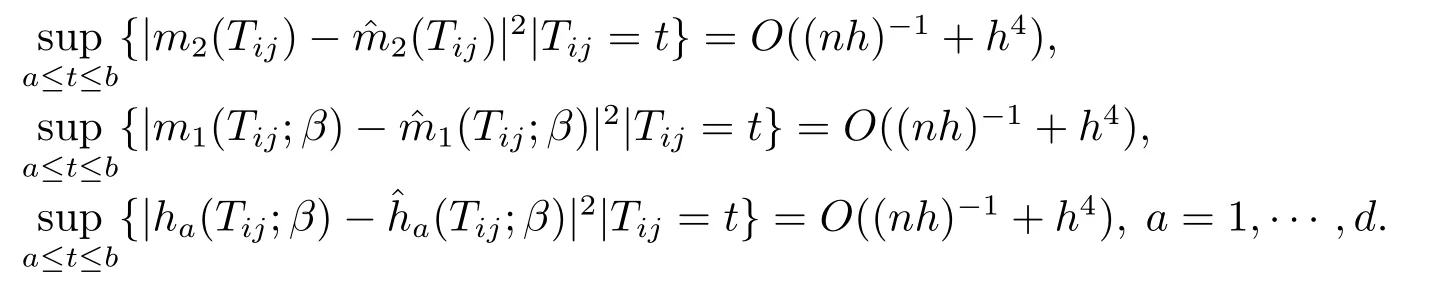
證僅給出以上第1個(gè)等式的證明,其余兩個(gè)等式可用同樣的方法證明.根據(jù)不等式(A+B)2≤2A2+2B2可以得到

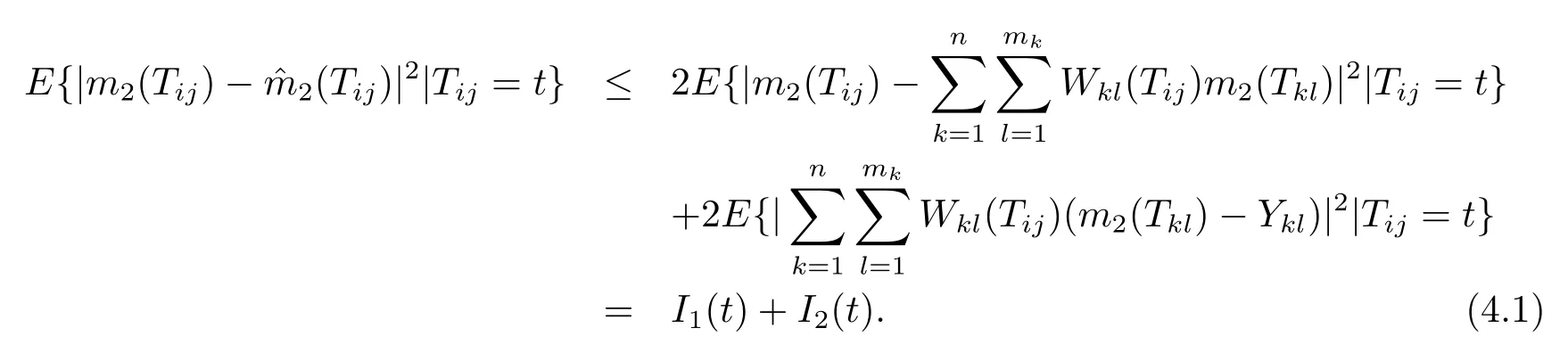
類似于文獻(xiàn)[10]中引理1中的證明,可以得到

基于這樣的事實(shí)E[Ykl-m2(Tkl)]=0,由條件C2-C4可得

結(jié)合(4.1)-(4.3)式,該結(jié)論得證.

引理2假設(shè)條件C1-C7成立,如果β為參數(shù)的真值,則有

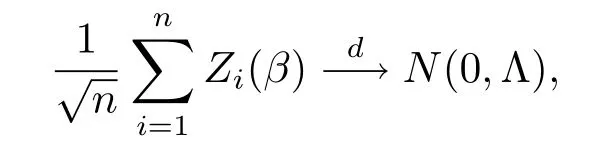
其中Λ的定義見定理2.2.

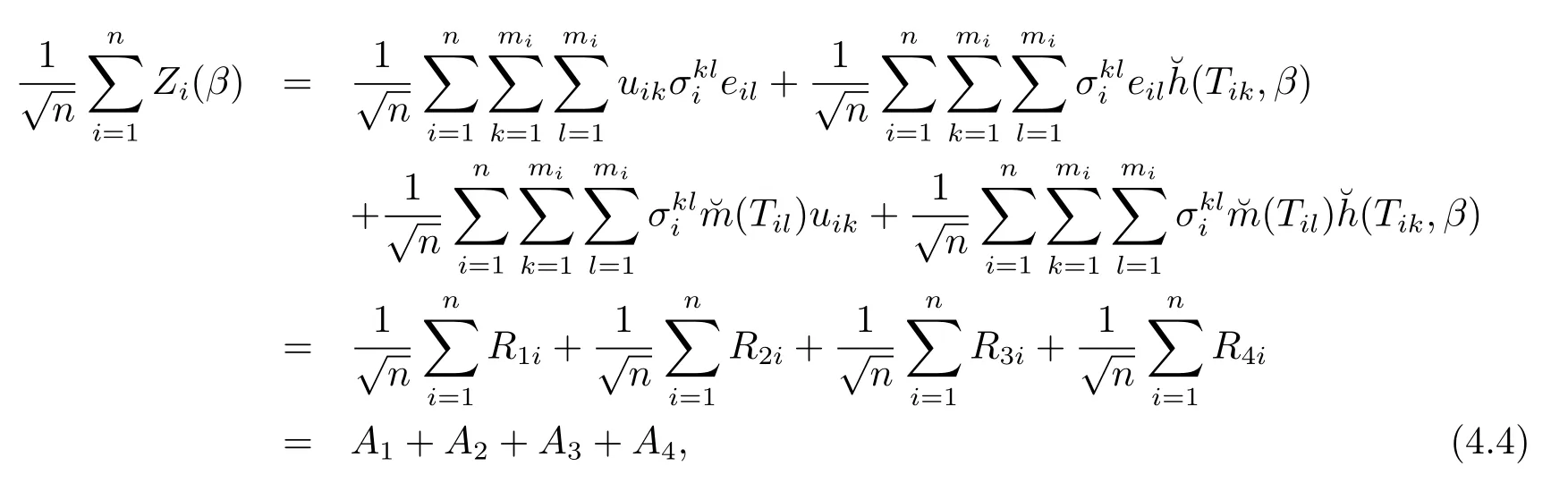
對(duì)A1,很容易得到E(A1)=0和cov(A1)=Λ.根據(jù)Lindeberg-Feller中心極限定理可以得到

根據(jù)引理1可以得到E||A2||2≤c{(nh)-1+h4}→0,因此得到類似的還有E||A3||2≤c{(nh)-1+h4}→0,即進(jìn)一步,根據(jù)引理1和Cauchy-Schwarz不等式,可以得到→0,由此推得

綜合以上討論,這就完成了該引理的證明.

引理3假設(shè)條件C1-C7成立,如果β為參數(shù)的真值,則有

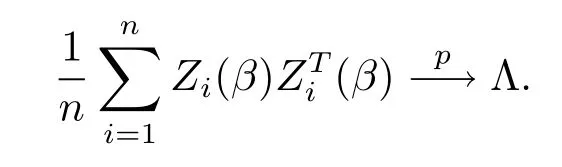
證仍然使用引理2中的記號(hào),并記Ji=R2i+R3i+R4i,則有

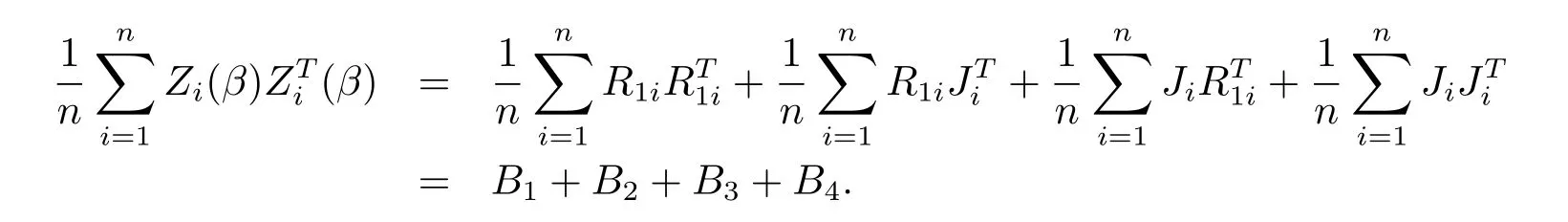
定理1的證明根據(jù)引理2-3和Owen[8]的思想,可以得到

對(duì)(2.6)式作用Taylor展式,并采用引理2-3,可以得到

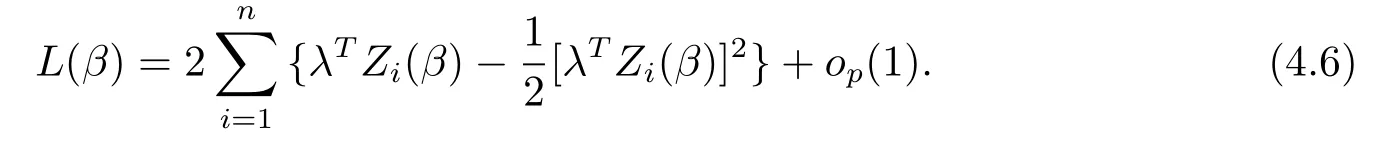
根據(jù)引理2和(4.5)式,(4.6)式,可以得到

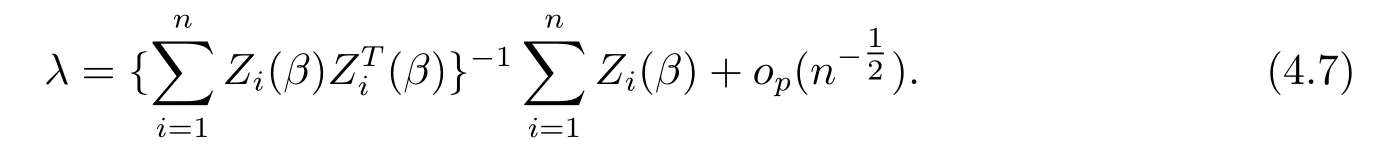
將(4.7)式代入(4.6)式,可以得到

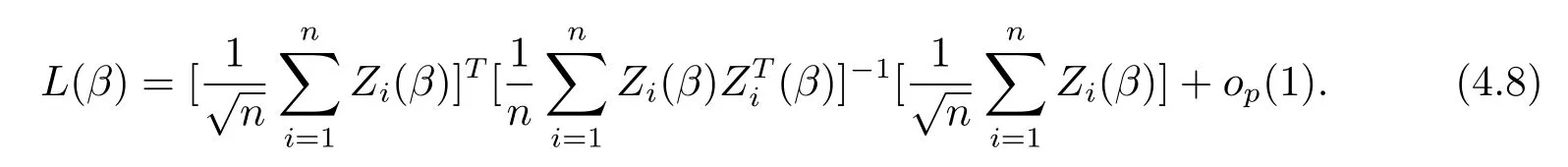
再結(jié)合(4.8)式,引理2-3,該定理得證.

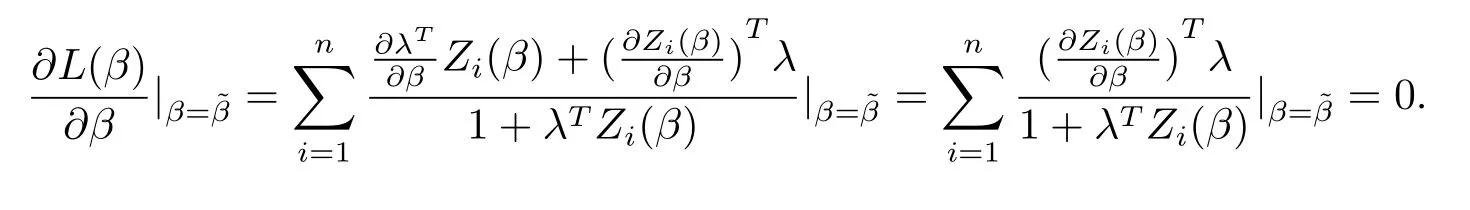
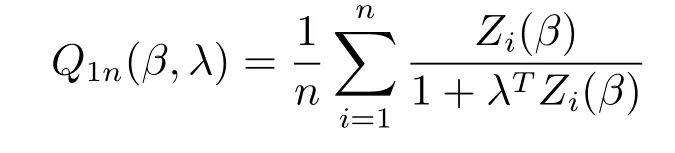
和

對(duì)Q1n(,)和Q2n(,)在點(diǎn)(β,0)作用Taylor展式,可以得到

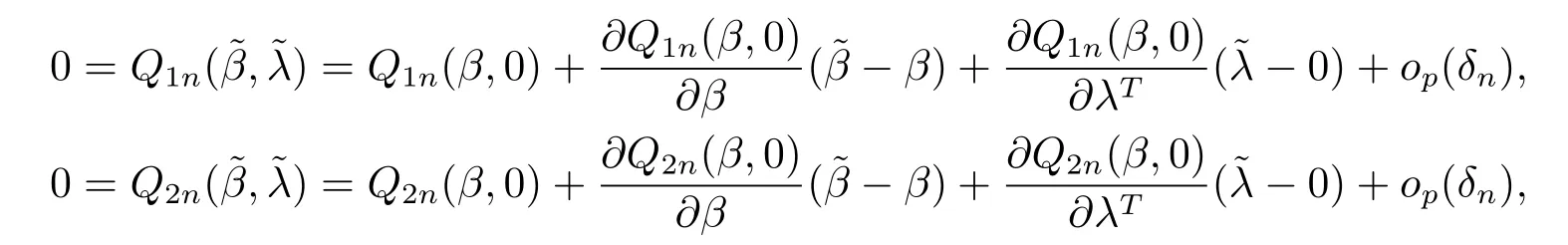
其中δn=||-β||+||||,因此可以得到

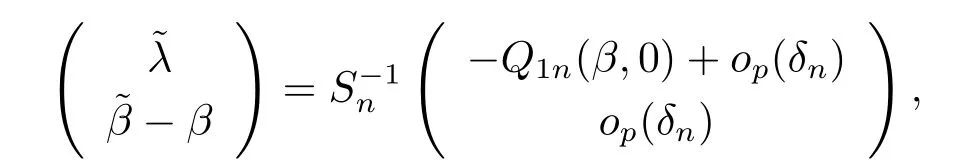
其中Sn=

根據(jù)(4.5)式并注意到Q1n(β,0)=Zi(β)=Op(n-1/2)可以得到δn=op(n-1/2).經(jīng)過(guò)簡(jiǎn)單計(jì)算可以得到

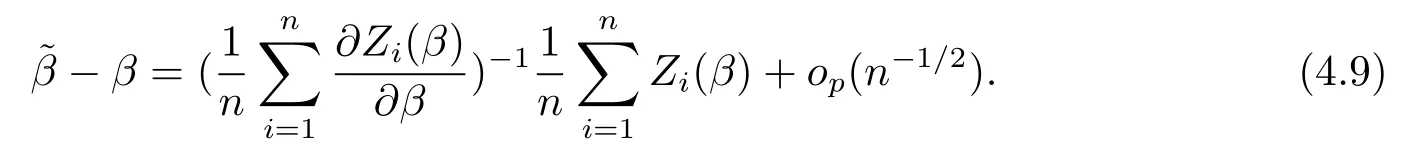
根據(jù)引理1可以證明

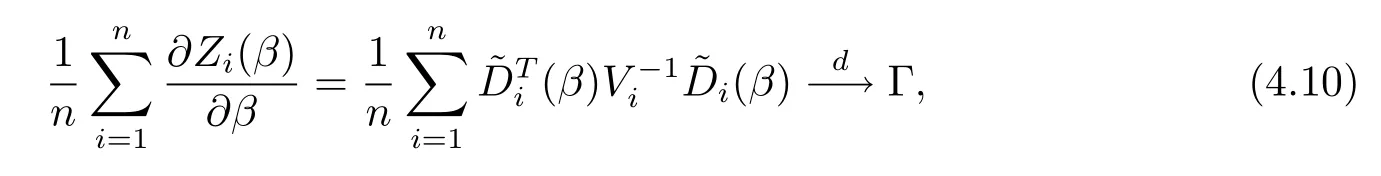
此式連同(4.9)式及引理2和Slutsky定理,可以證得該定理.

[1]Li R,Nie L.Efficient statistical inference procedures for partially nonlinear models and their applications[J].Biometrics,2008,64(3):904-911.

[2]Xiao Y T,Tian Z,Li F X.Empirical likelihood-based inference for parameter and nonparametric function in partially nonlinear models[J].J.Korean Stat.Soc.,2014,43(4):367-379.

[3]馮三營(yíng),李高榮,薛留根,陳放.非線性半?yún)?shù)EV模型的經(jīng)驗(yàn)似然置信域[J].高校應(yīng)用數(shù)學(xué)學(xué)報(bào),2010, 25(1):53-63.

[4]馮三營(yíng),薛留根.非線性半?yún)?shù)EV模型的最大經(jīng)驗(yàn)似然估計(jì)[J].數(shù)學(xué)物理學(xué)報(bào),2012,32(4):729-743.

[5]肖燕婷,田錚,孫瑾.核實(shí)數(shù)據(jù)下非線性半?yún)?shù)EV模型的估計(jì)[J].數(shù)學(xué)雜志,2015,35(5):1075-1085.

[6]武大勇,李鋒.隨機(jī)缺失下半?yún)?shù)回歸模型的最大經(jīng)驗(yàn)似然估計(jì)[J].山東大學(xué)學(xué)報(bào),2015,50(4):20-23.

[7]劉強(qiáng).缺失數(shù)據(jù)下非線性半?yún)?shù)EV模型的估計(jì)[J].系統(tǒng)科學(xué)與數(shù)學(xué),2010,30(9):1236-1250.

[8]Owen A.Empirical likelihood ratio confidence intervals for a single function[J].Biometrika,1988, 75(2):237-249.

[9]Li G R,Tian P,Xue L G.Generalized empirical likelihood inference in semiparametric regression model for longtitudianl data[J].Acta Math.Sinica,Engl.Ser.,2008,24(12):2029-2040.

[10]薛留根,朱力行.縱向數(shù)據(jù)下部分線性模型的經(jīng)驗(yàn)似然推斷[J].中國(guó)科學(xué),2007,37(1):31-44.

2010 MR Subject Classification:62G05

GENERALIZED EMPIRICAL LIKELIHOOD INFERENCE FOR PARTIALLY NONLINEAR MODELS WITH LONGITUDINAL DATA

XIAO Yan-ting,SUN Xiao-qing,SUN Jin
(Department of Applied Mathematics,Xi’an University of Technology,Xi’an 710054,China)

In this paper,we study the construction of confidence region for unknown parameter in partially nonlinear models with longitudinal data.By empirical likelihood method, the generalized empirical log-likelihood ratio for parameter in nonlinear function is proposed and shown to be asymptotically chi-square distribution.At the same time,the maximum empirical likelihood estimator of the parameter in nonlinear function is obtained and asymptotic normality is proved.

longitudinal data;partially nonlinear models;empirical likelihood;confidence region

MR(2010)主題分類號(hào):62G05O212.7

A

0255-7797(2016)06-1238-07

?2015-10-23接收日期:2016-02-25

國(guó)家自然科學(xué)基金(61303223;11501443);陜西省自然科學(xué)基金(2015JM1039);陜西省教育廳基金(2016JK1545);西安理工大學(xué)校基金(2015CX009

肖燕婷(1981-),女,陜西西安,講師,主要研究方向:非(半)參數(shù)統(tǒng)計(jì).