一類四階非線性波動方程解的爆破與衰減

李寧,雷倩,楊晗

(西南交通大學數學學院,四川成都611756)

一類四階非線性波動方程解的爆破與衰減

李寧,雷倩,楊晗

(西南交通大學數學學院,四川成都611756)

本文研究了非線性阻尼項與源項的競爭對具有強阻尼項的四階波動方程解的影響.利用不動點原理和勢井方法給出了方程局部弱解存在唯一性滿足的條件,證明了當m＜p且初始能量E(0)＜0時,解將在有限時間內爆破.同時對m,p的大小關系不加任何限制但存在t0使0＜E(t0)＜d的情況下,利用穩定集,研究了整體解的存在性,并得到了解的能量衰減估計.最后借助修正的能量泛函,指出當m≥p時弱解也是整體存在的,推廣并改進了文獻[1-6]中的結果.

強阻尼項;四階波動方程;勢井;爆破;衰減估計

1　引言

本文將研究如下具有強阻尼項的四階非線性波動方程的初邊值問題

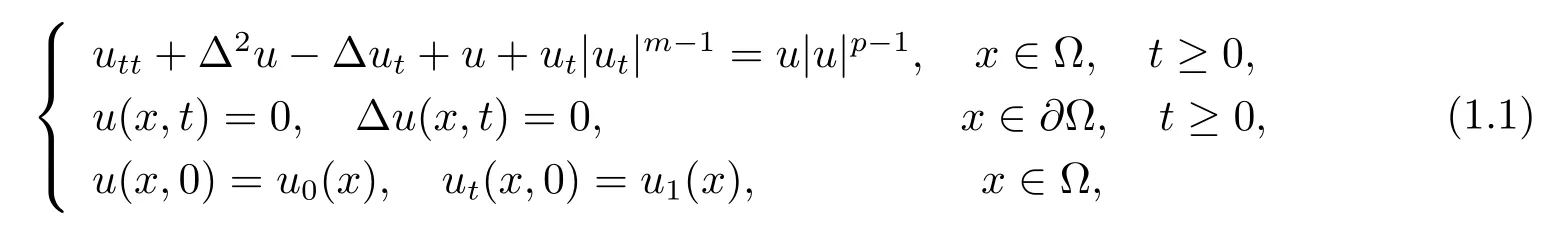
其中m,p＞1,Ω是Rn中具有光滑邊界的有界區域.問題(1.1)描述的是粘彈性微觀物體的實際運動過程.事實上,物體在運動時周圍的介質產生的阻尼和力源,特別是強阻尼,對物體內部能量的積聚起著重要的耗散作用,因此在實際模型中需要加以考慮.

當方程(1.1)中的強阻尼項?ut和線性項u缺失時,非線性弱阻尼項和非線性源項之間的相互作用對解的影響已被很多作者考慮過.2002年,Messaoudi在文[1]中指出當m≥p時,初始值的弱解是整體存在的,當m＜p且初始能量E(0)＜0時,解將在有限時間里爆破;同時,Messaoudi在文[2]中拓展了在文[1]中的結果,指出當初始數據選擇合適的值時,不需討論m,p的大小關系,得到了整體解的存在性定理和衰減估計.2008年,韓獻軍、薛紅霞在文[3]中得到了類似的結論,他們利用勢井理論構造了穩定集,在初值位于穩定集時,得到了弱解是整體存在的且具有衰減性質;2010年,尹麗、薛紅霞、韓獻軍在文[4]中利用勢井理論構造了不穩定集,證明了當m＜p且初始能量非負時,解將在有限時刻發生爆破.2009年,Chen和Zhou在文[5]中,對m＜p且初始能量為正的情形,證明了整體解的不存在性,關于解的爆破結論與文[4]中的結論是一樣的.

2013年,在文[6]中,Chen和Liu考慮了二階波動方程的情形,即方程(1.1)中的?2u被?u代替,同時線性項u缺失時,證明了局部解的存在唯一性,同時利用勢井法,研究了整體解的存在性,解的多項式和指數衰減.最后指出當初始數據足夠大或E(0)＜0時,能量將隨著時間呈指數式增長.

以上文獻[1-5]都是沒有強阻尼項時的情形,研究非線性弱阻尼項的波動方程解的存在性、爆破及衰減估計,文獻[6]研究了具有強阻尼項二階的非線性波動方程.對帶有強阻尼項四階的非線性波動方程,目前結論很少且有很多問題有待解決.本文將在以上文獻的基礎上研究具有強阻尼項的四階非線性波動方程(1.1)解的存在性、爆破和能量衰減.

2　局部解的存在唯一性

為證明局部弱解的存在性,下面先給出幾個引理.

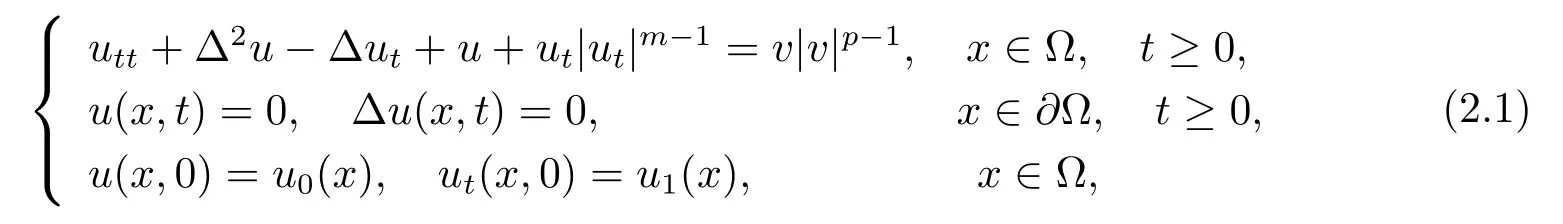
存在唯一的解u(x,t),并且滿足

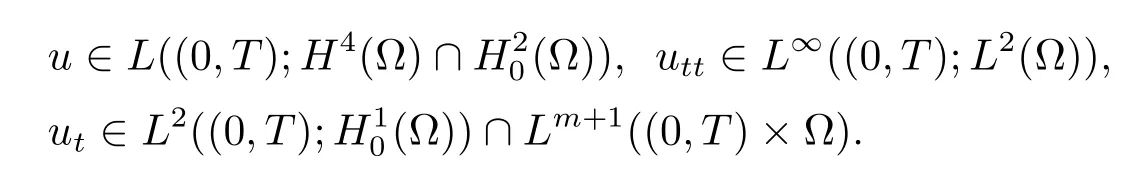
此引理的證明類似于文獻[7]中第一章定理3.1的證明,略去證明過程.

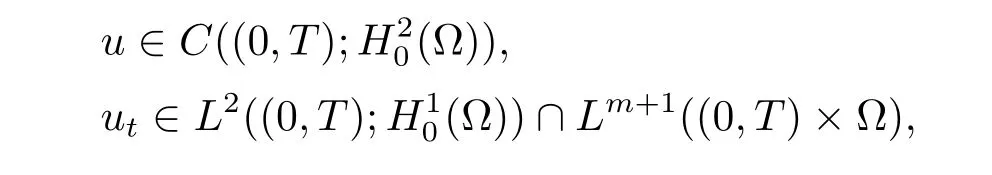
并且成立能量等式

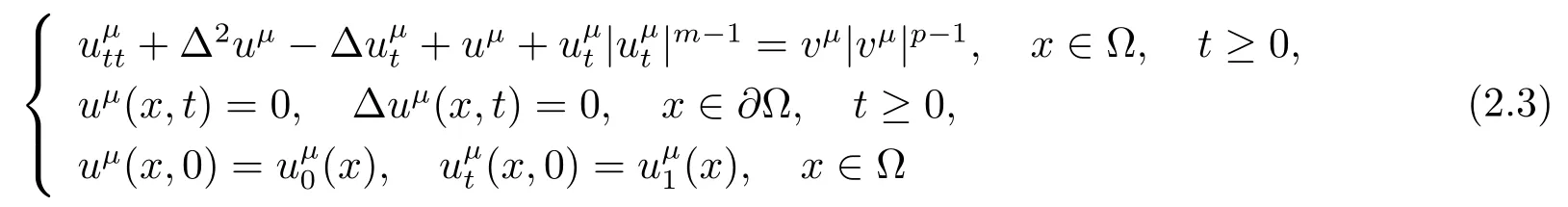
存在唯一的解{uμ}滿足

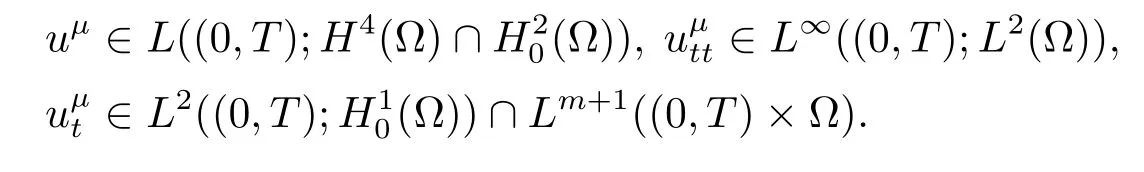
下面證明{uμ}是

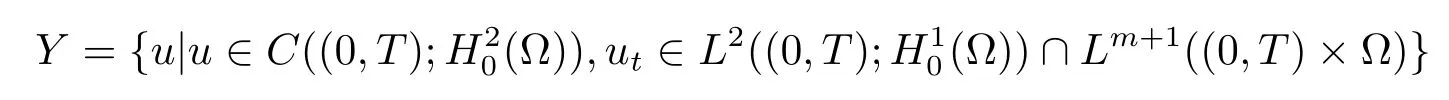
中的Cauchy列.為此,令U=uμ-uν,V=vμ-vν,則U滿足下面方程

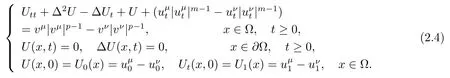
在方程(2.4)兩端同時乘以Ut,并且在(0,T)×Ω上積分得

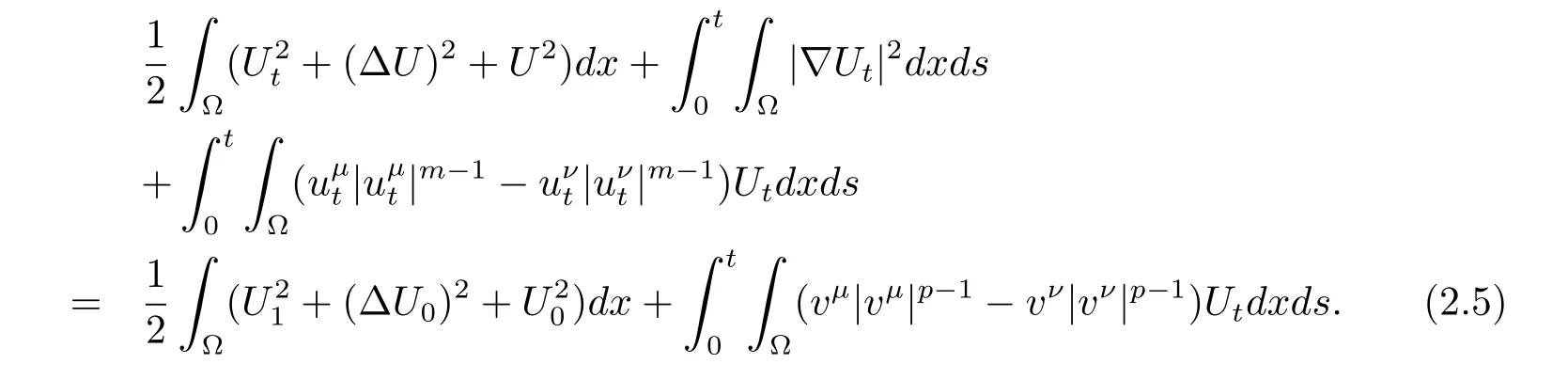
下面來估計(2.5)式的最后一項

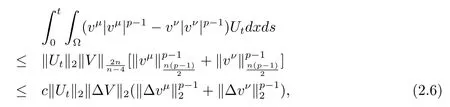
其中c是一個僅依賴于Ω的常數.

由(|α|m-1α-|β|m-1β)(α-β)≥c|α-β|m及(2.6)式得(2.5)式變為

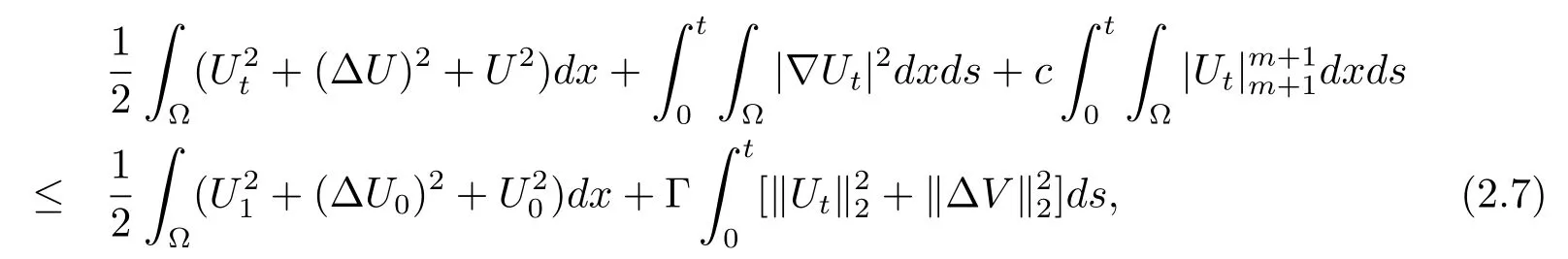
下面證明極限u(x,t)是方程(2.1)在以下式子意義下的弱解:即對每個θ∈(Ω),有

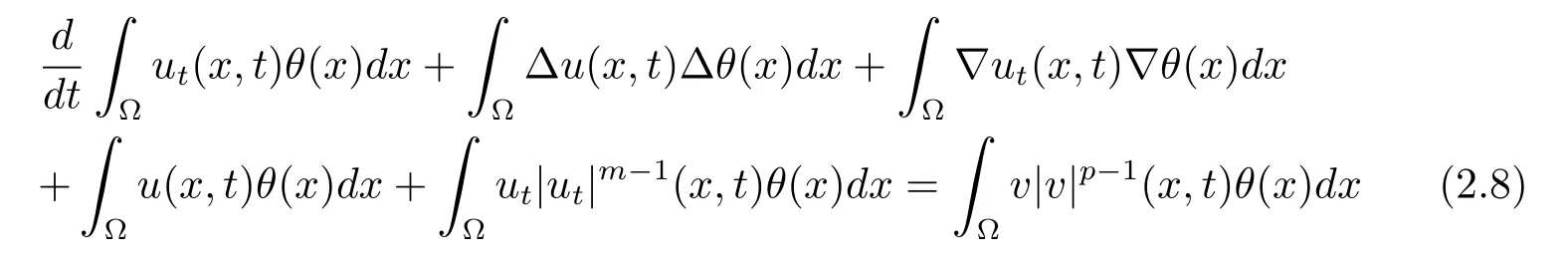
對幾乎處處的t∈[0,T]成立.

事實上,在(2.3)式兩端同時乘以θ,并在Ω上積分可得

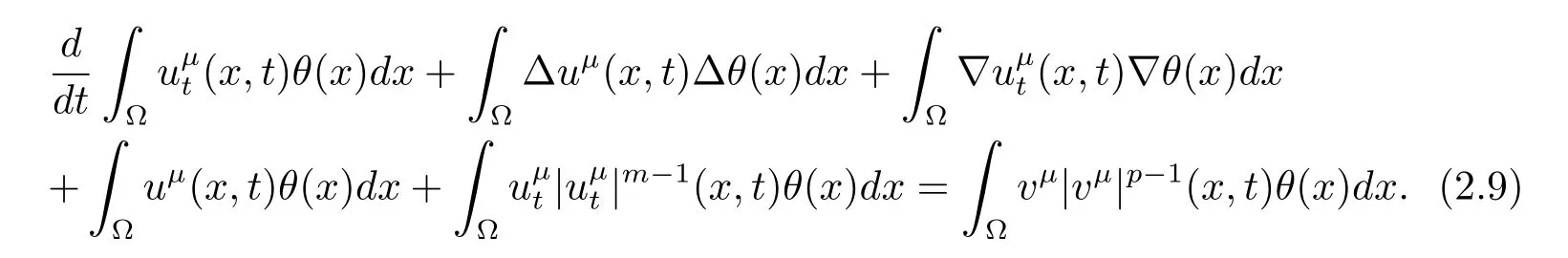
令μ→∞,可知在C([0,T])中成立

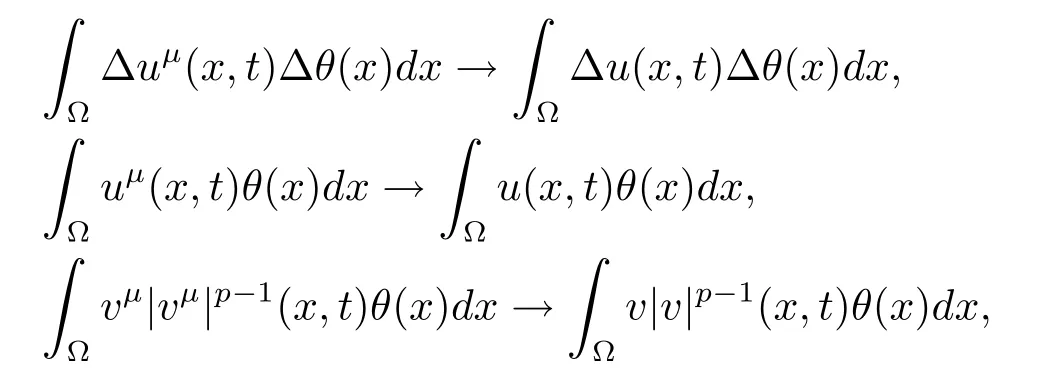
且在L1([0,T])中成立

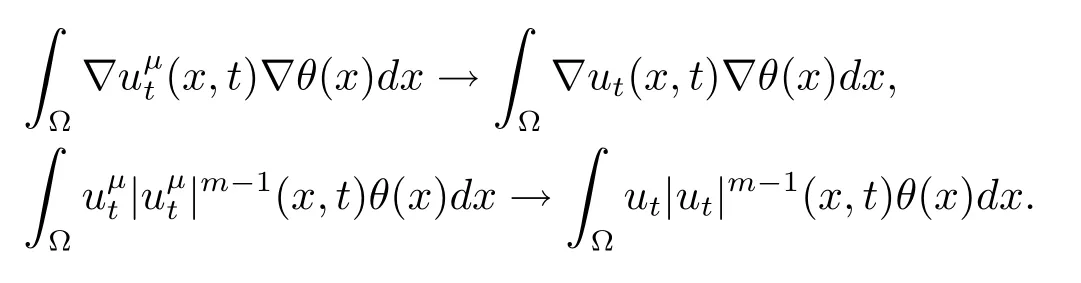
下證唯一性,取v1,v2,令u1,u2分別為方程(2.1)相應于v1,v2的兩個解.令U=u1-u2,則

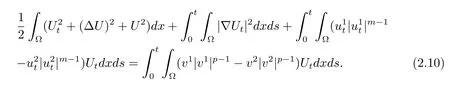
若v1=v2,則由(2.10)式可知U=0,即唯一性得證.

下面給出局部弱解存在唯一性的定理.

證取M＞0充分大,設X(M,T)是由Y中滿足方程(2.1)中的初邊值條件,并且滿足下面條件的w組成的集合

定義映射u=f(v):X(M,T)→Y.其中u(x,t)是方程(2.1)的唯一解.

下面證明當M充分大,T＞0充分小時,f是一個從X(M,T)到X(M,T)的映射.

由能量等式(2.2)知

因此

其中c與M無關,選取M充分大,T＞0充分小,使(2.11)式成立,故f是一個從X(M,T)到X(M,T)的映射.

下證f是一個壓縮映射.

在(2.13)式兩端同時乘以Ut,并在(0,t)×Ω上積分,可得

由式(2.6)和(2.7)知

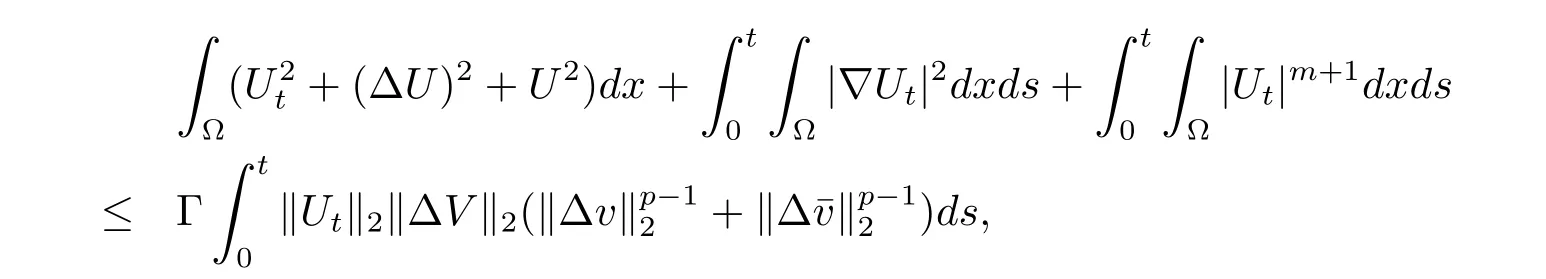
因此

選取T充分小使ΓTMp-1＜1,則由(2.15)式可知f是一個壓縮映射.由壓縮映射原理可知,存在唯一的u=f(u),即u是方程(1.1)的解,并由(2.14)式可知解的唯一性.

3　解的爆破

先給出證明解的爆破的一個有關引理.

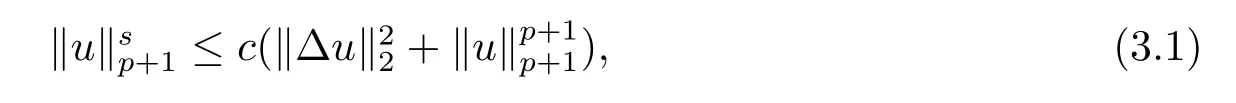
證由Sobolev嵌入定理即可證明.

為了下面證明中表達方便,這里定義與方程(1.1)相關的能量泛函為

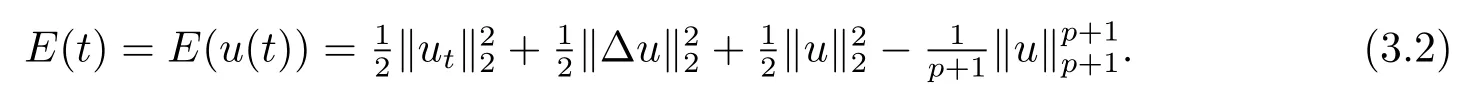
令

證由能量等式可得

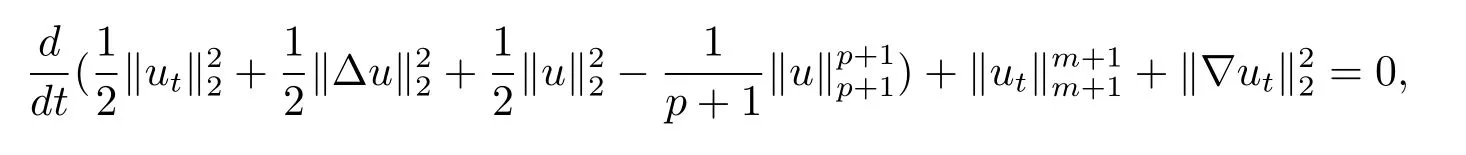
則對幾乎處處的t∈[0,T),

故H(t)是遞增函數,因此由式(3.2)、(3.3)和E(0)＜0可知,對任意的t∈[0,T),

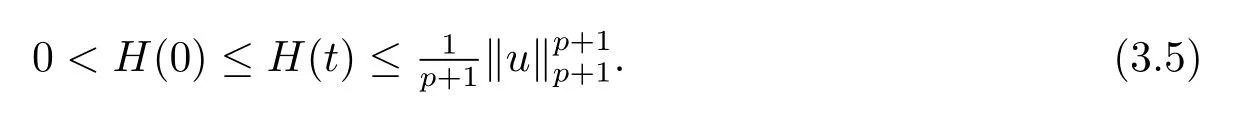
定義

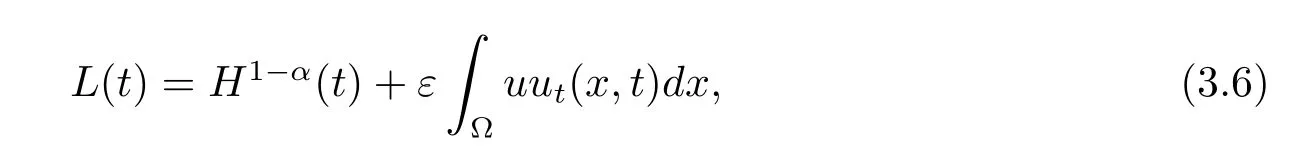
其中ε充分小,將在下文中選定,并且

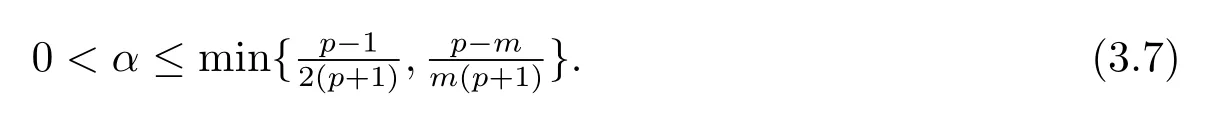
對L(t)求導,并由方程(1.1)知

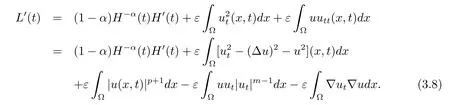
利用Young不等式

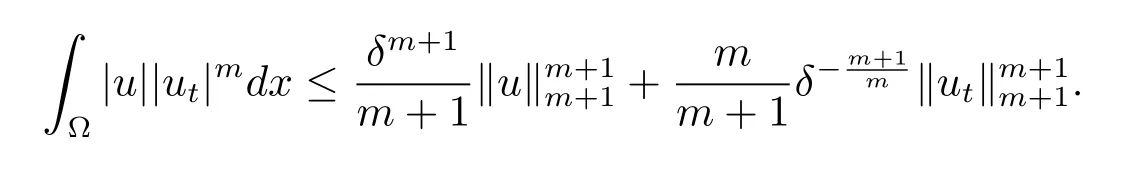
同時

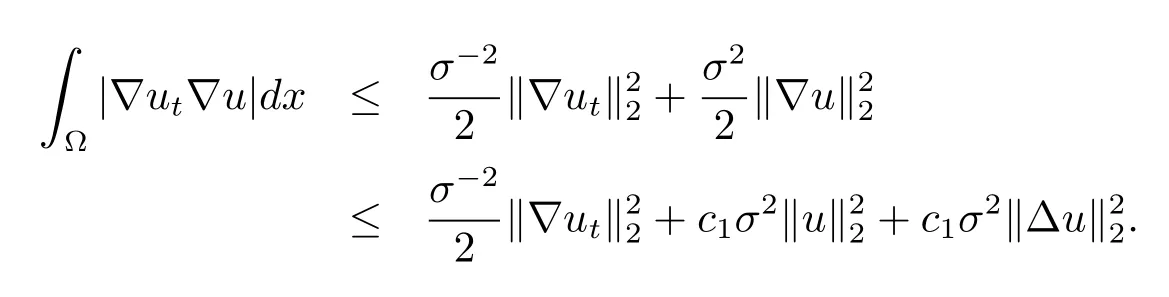
將以上兩個不等式帶入(3.8)式得

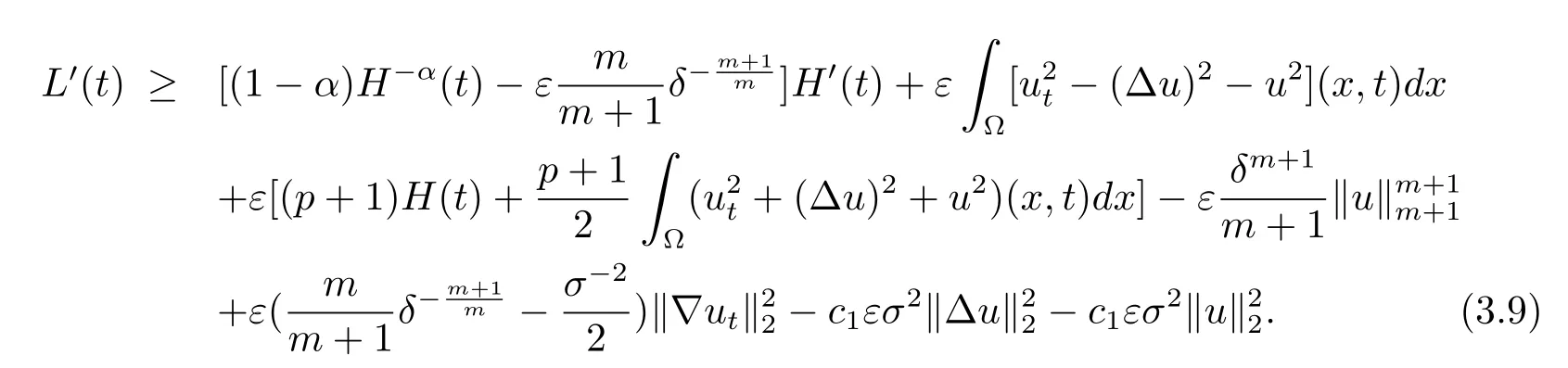
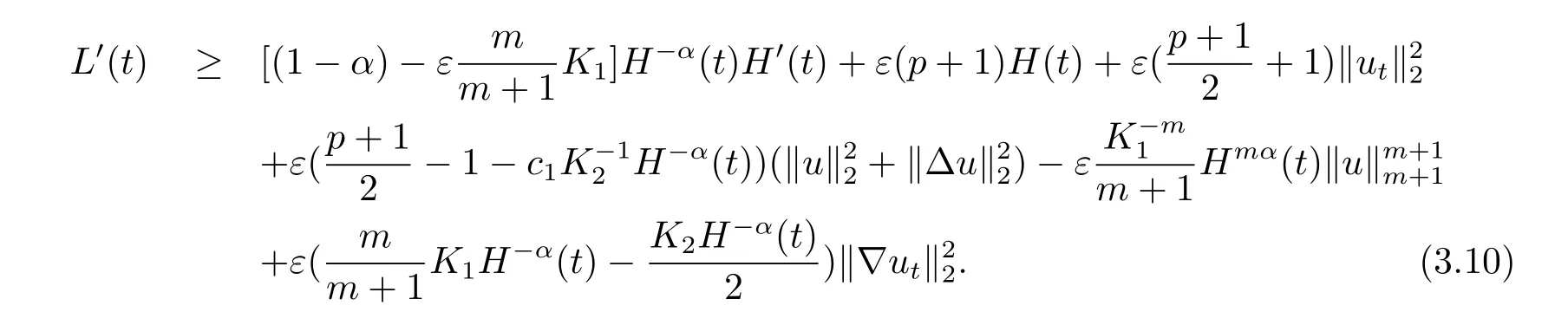
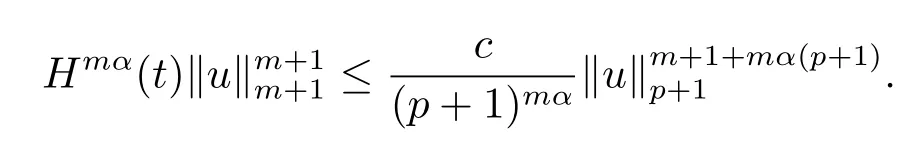
取s=m+1+mα(p+1)≤p+1,由引理3.1和(3.7),(3.10)式知

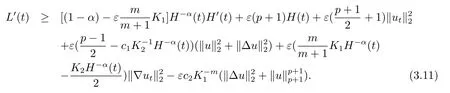
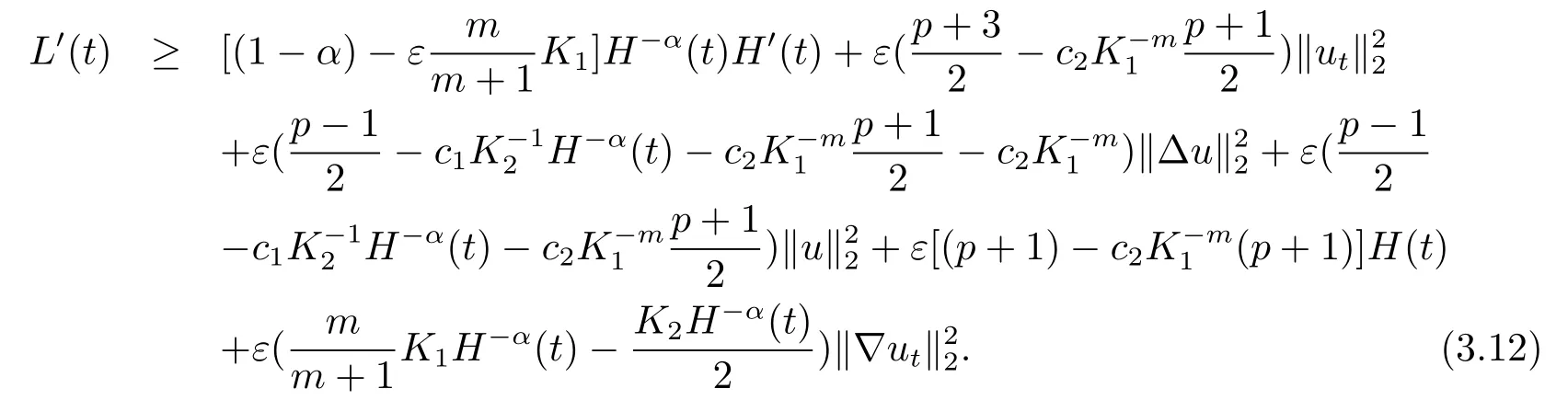
選取K1,K2充分大,且K1＞K2,使在(3.12)式中系數為正,則可得

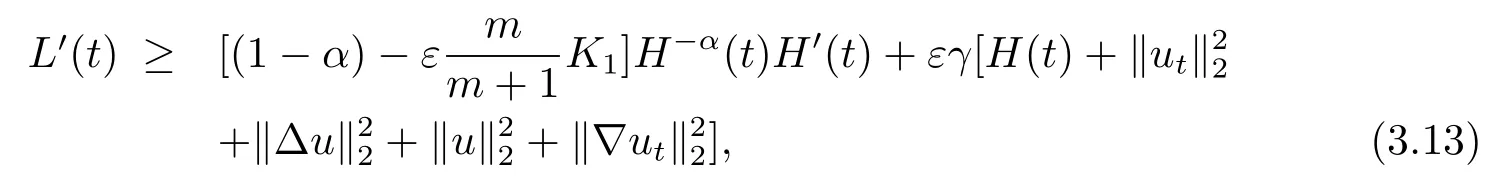
其中

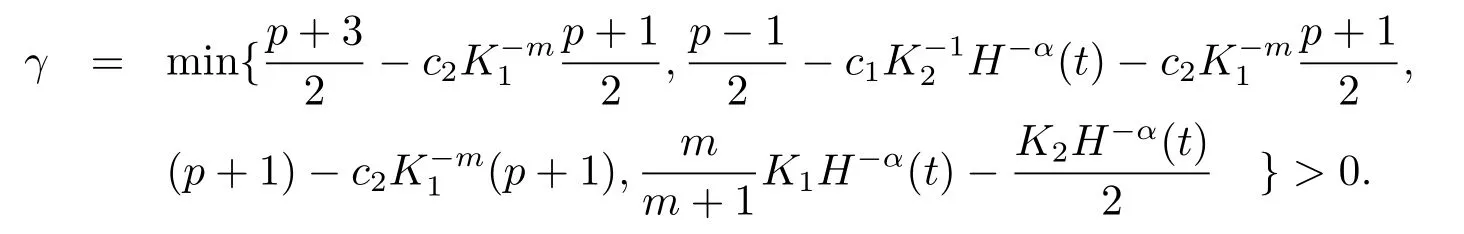
當K1取定時,選取ε充分小使得(1-α)-K1≥0,且

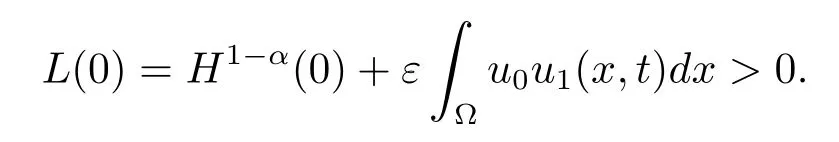
故由(3.13)式知

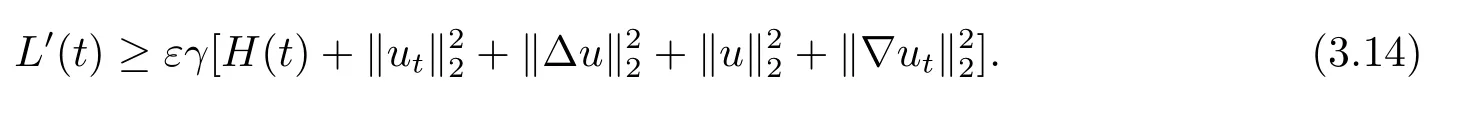
因此可知

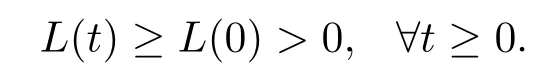
下面來估計(3.6)式中的第二項

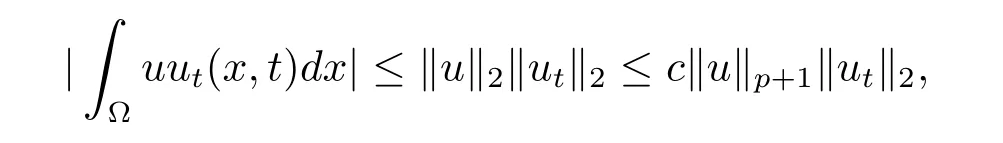
由Young不等式可知

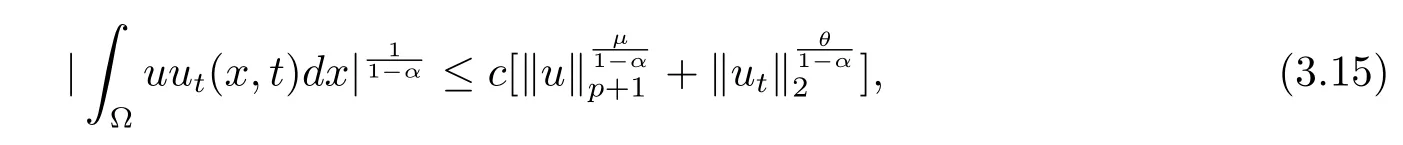
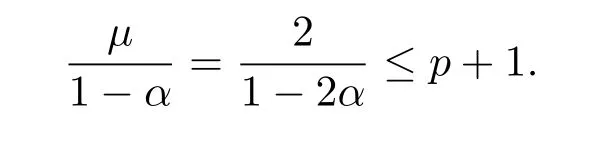
由(3.15)式可知

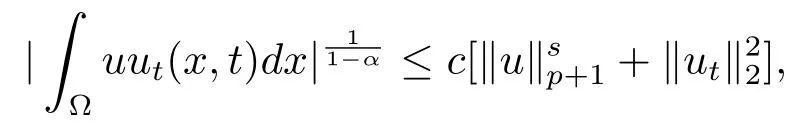
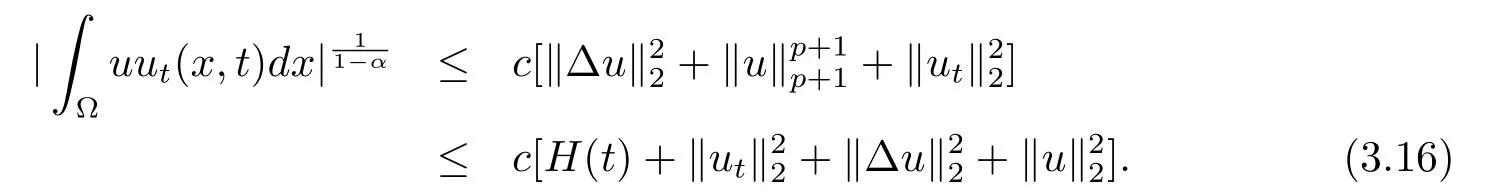
因此可得

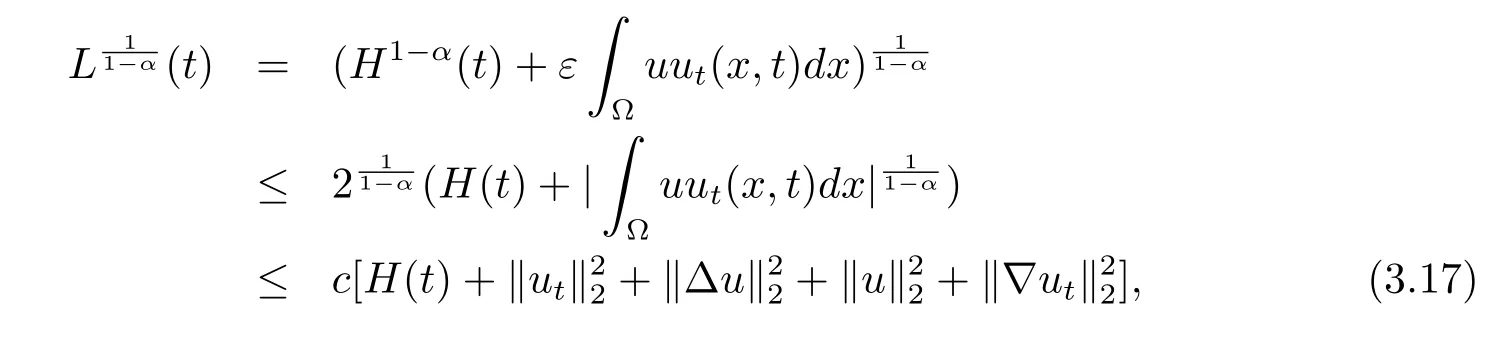
由(3.14),(3.17)式可知

其中Γ是一個依賴于c,γ,ε的常數.令(3.18)式在(0,t)上積分得

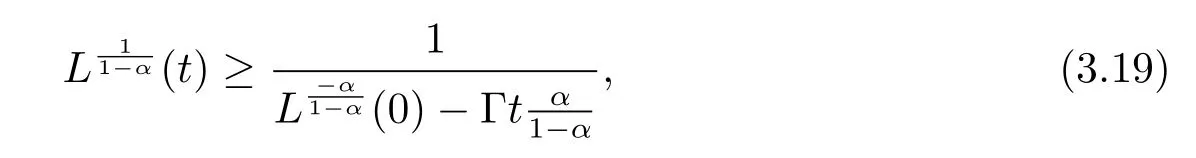
4　整體解的存在性及其能量衰減估計

4.1準備工作

此部分先引入勢井,同時給出相關引理.

定義與方程(1.1)相關的能量泛函為

記

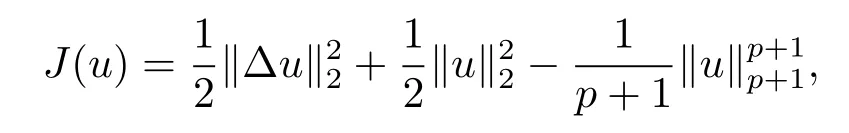
勢井深度

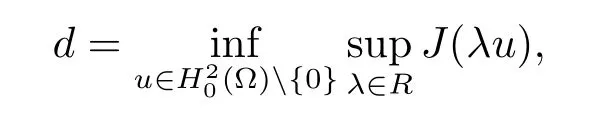
穩定集

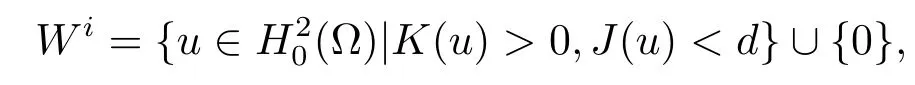
其中

證由d的定義及微分知識可得到證明.

引理4.2 Wi為中的有界集.

證直接由Wi的定義可得到證明.

證假設存在t1∈[t0,Tmax)使得t∈[t0,t1)時,u(x,t)∈Wi,而u(x,t1)/∈Wi.由Wi的定義及J(u)和K(u)關于t的連續性知

(1)J(u(t1,·))=d或

(2)K(u(t1,·))=0.

根據E(t0)＜d和能量等式E(t1)=E(t0)-得

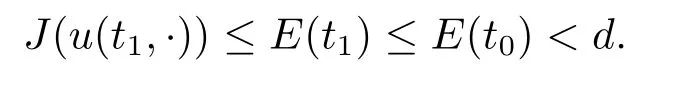
顯然J(u(t1,·))=d是不可能的,即(1)式不成立.

若K(u(t1,·))=0.則

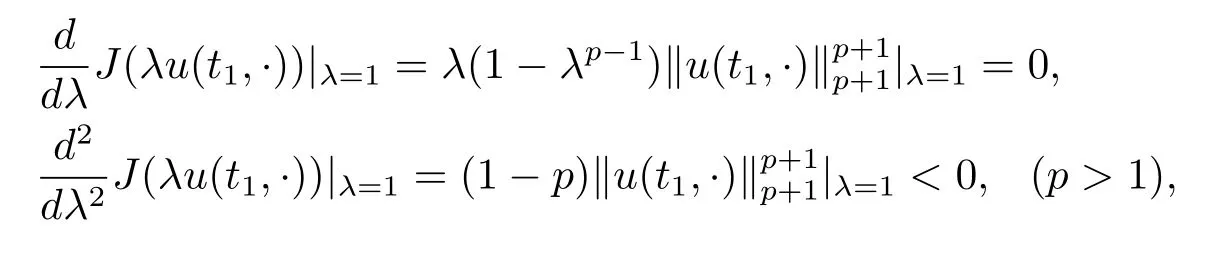
引理4.4在引理4.3的假設下,對任意t∈[t0,Tmax),問題(1.1)的解u(x,t)成立如下不等式

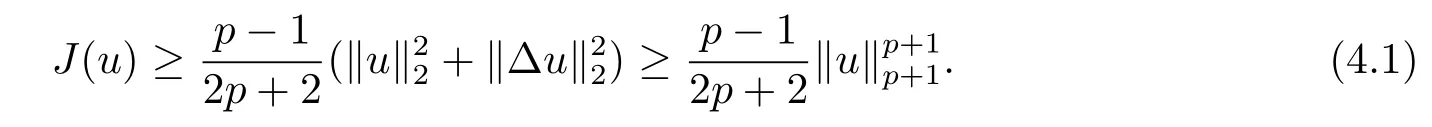
其中t∈[t0,Tmax).

證根據引理4.3得,對任意t∈[t0,Tmax),K(u)=+‖?u≥0,則

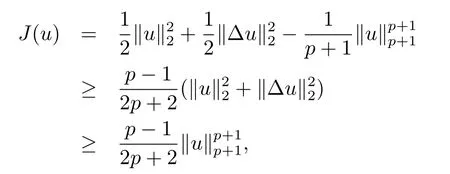
其中t∈[t0,Tmax).

引理4.5在引理4.4的條件下,有

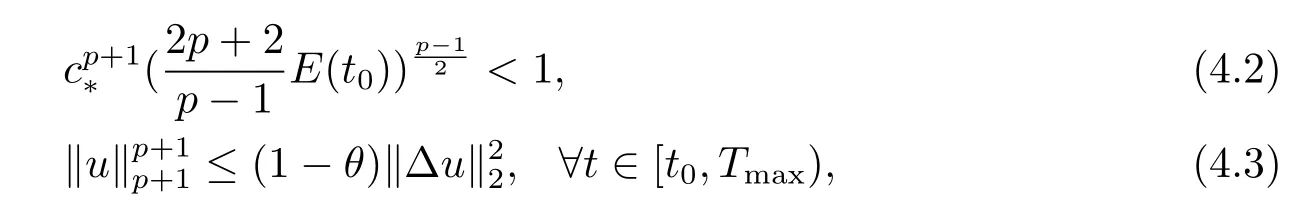
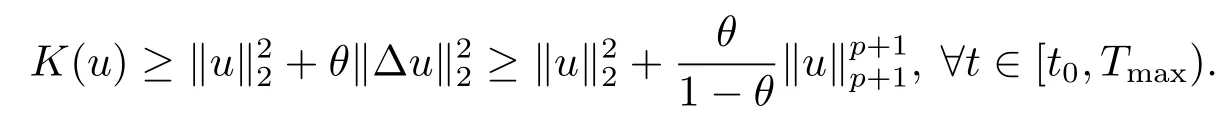
證由d的定義可得(4.2)式成立.由引理4.4知

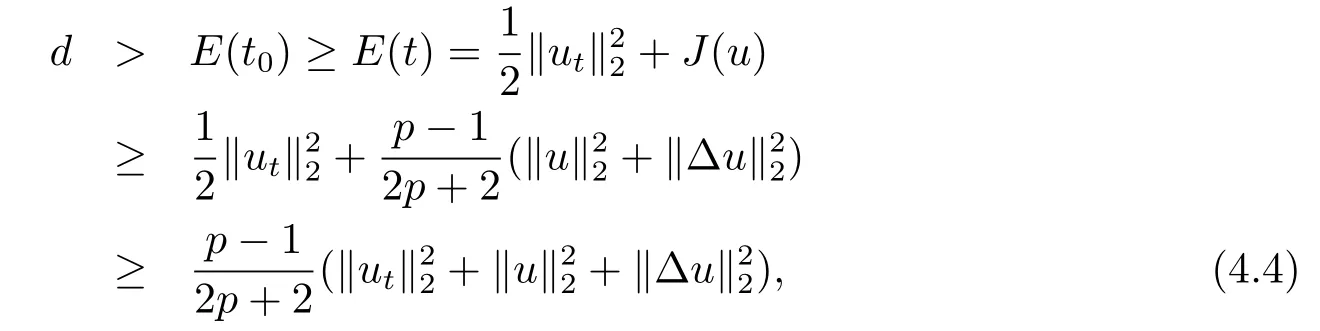
則由Sobolev嵌入定理及(4.4)式得

進而

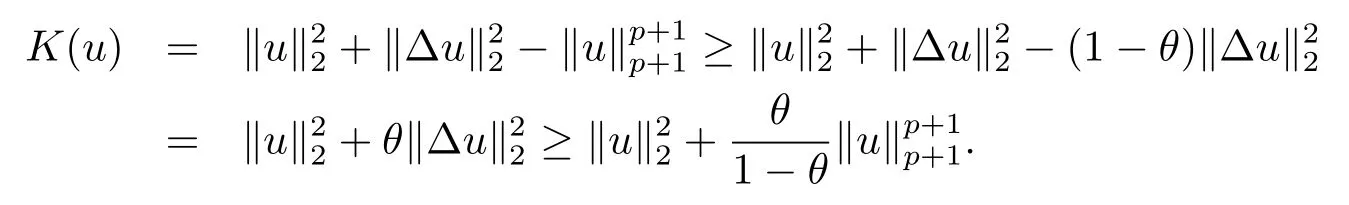
引理4.6設F:R+→R+為一個非增函數,若存在p≥1,A＞0,使得

則

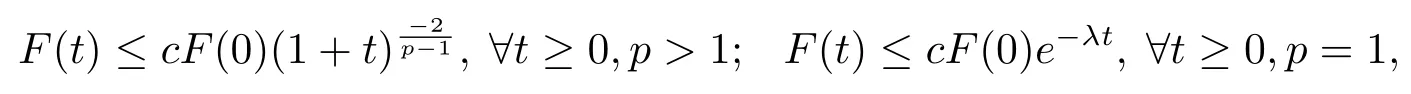
其中c,λ是不依賴于F(0)的正常數.

此引理的證明見文獻[8].

注引理4.5和引理4.6在能量衰減估計中有重要作用.

4.2整體解的存在性及其能量衰減估計

首先給出整體解的存在性定理.

證由引理4.4和E＇(t)＜0得

其中t∈[t0,Tmax),由上式和連續性原理[9]得到整體解,即Tmax=∞.故整體解的存在性得證.

下面作整體解的能量衰減估計.

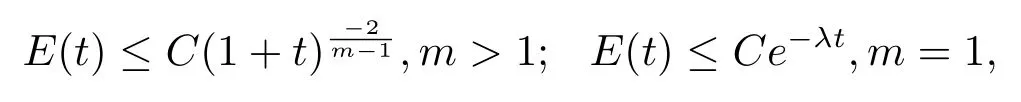
其中C,λ是正常數,且C依賴于E(t0).

證以下要證明

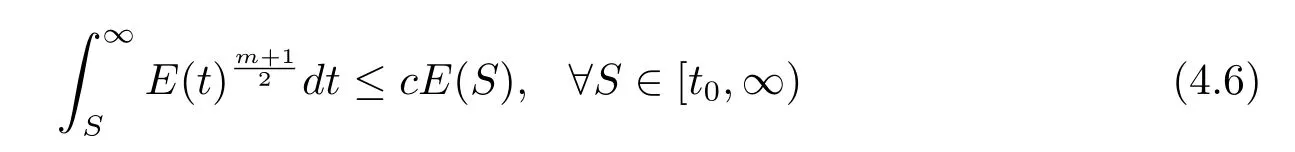
成立,進而利用引理4.6,可得結論成立.

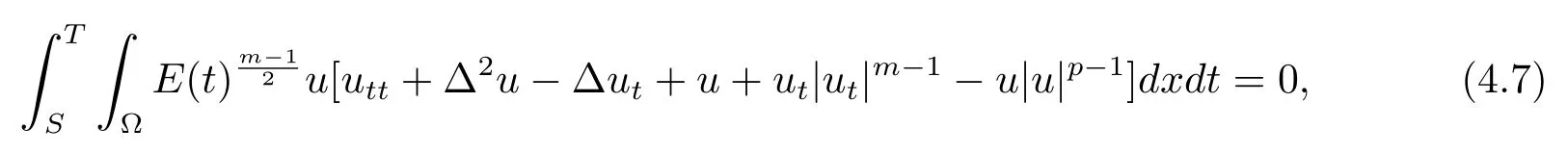
其中

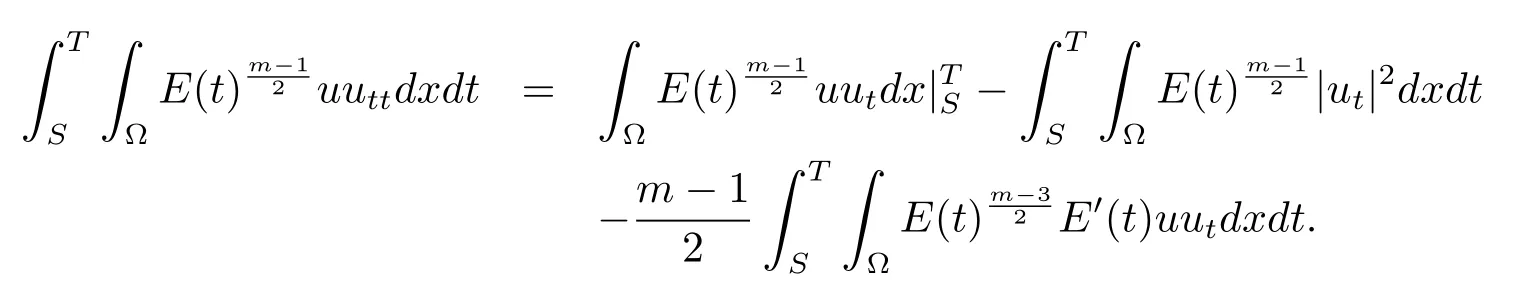
將上式代入(4.7)式得

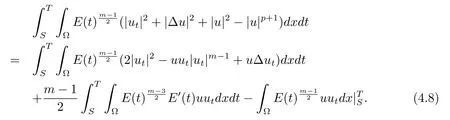
由E＇(t)≤0及(4.5)式得

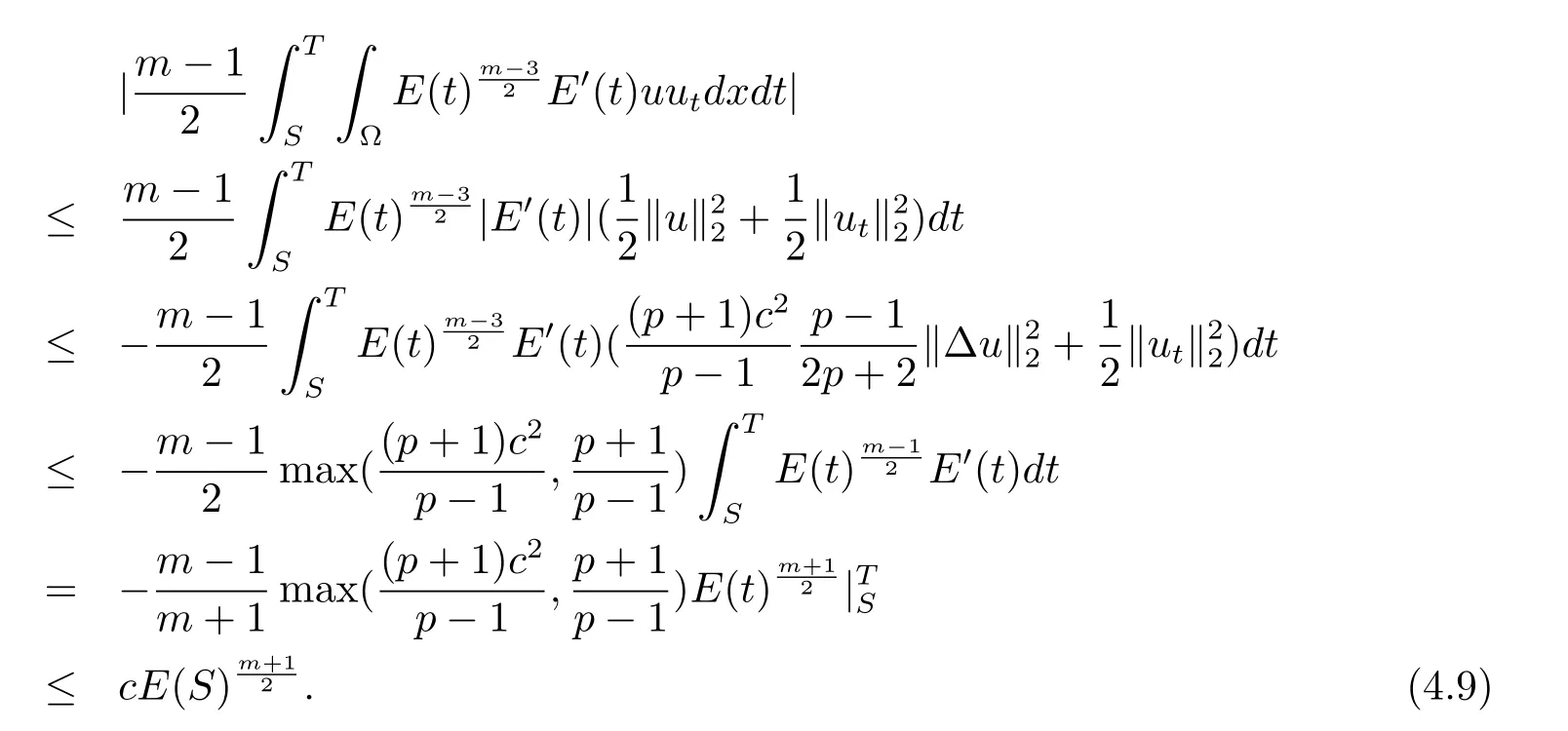
類似的

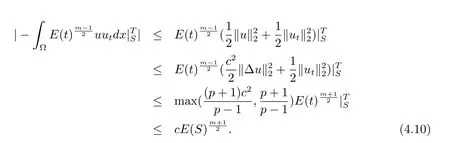
又注意到0＜θ＜1,由引理4.5得

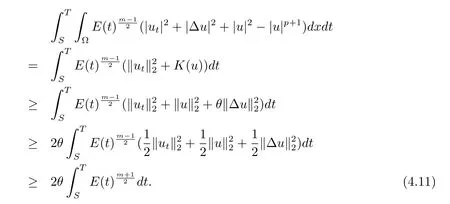
將(4.9)-(4.11)式代入(4.8)式得

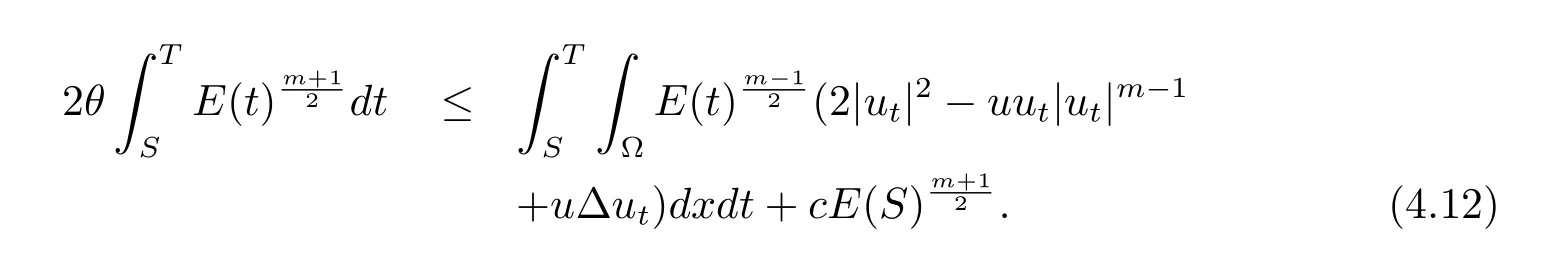
由Young不等式及E＇(t)=-得

又由Young不等式,(4.5)式及E＇(t)≤0得

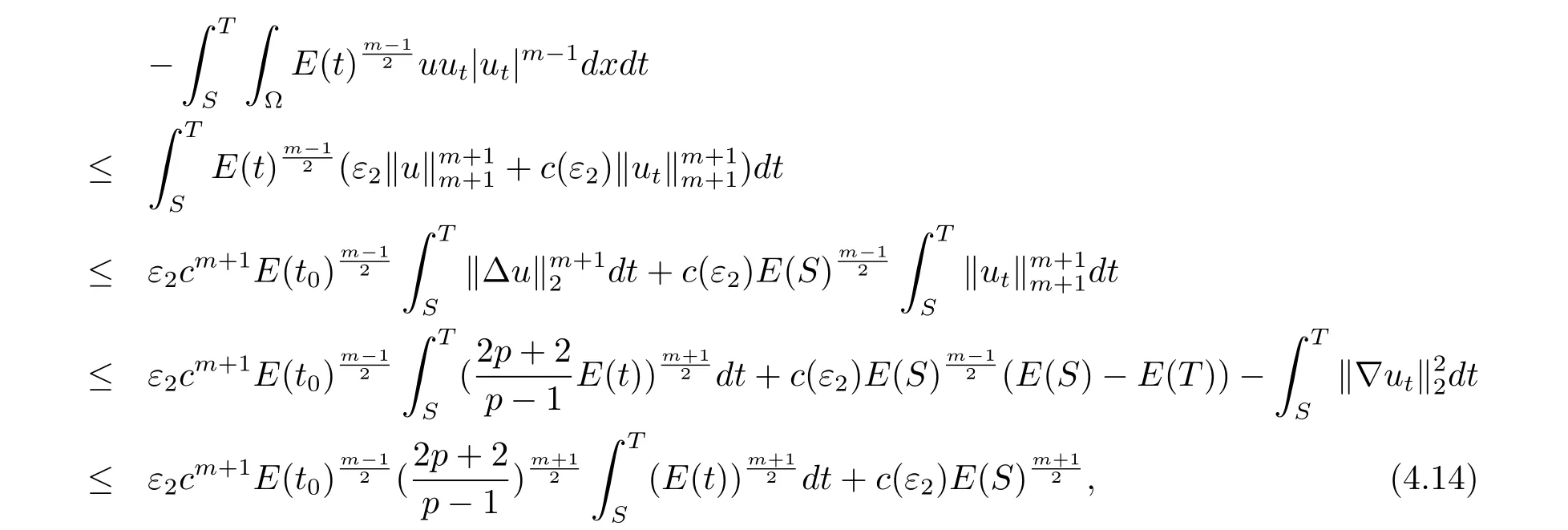
這里c(ε1),c(ε2)是依賴于ε1,ε2的正常數.

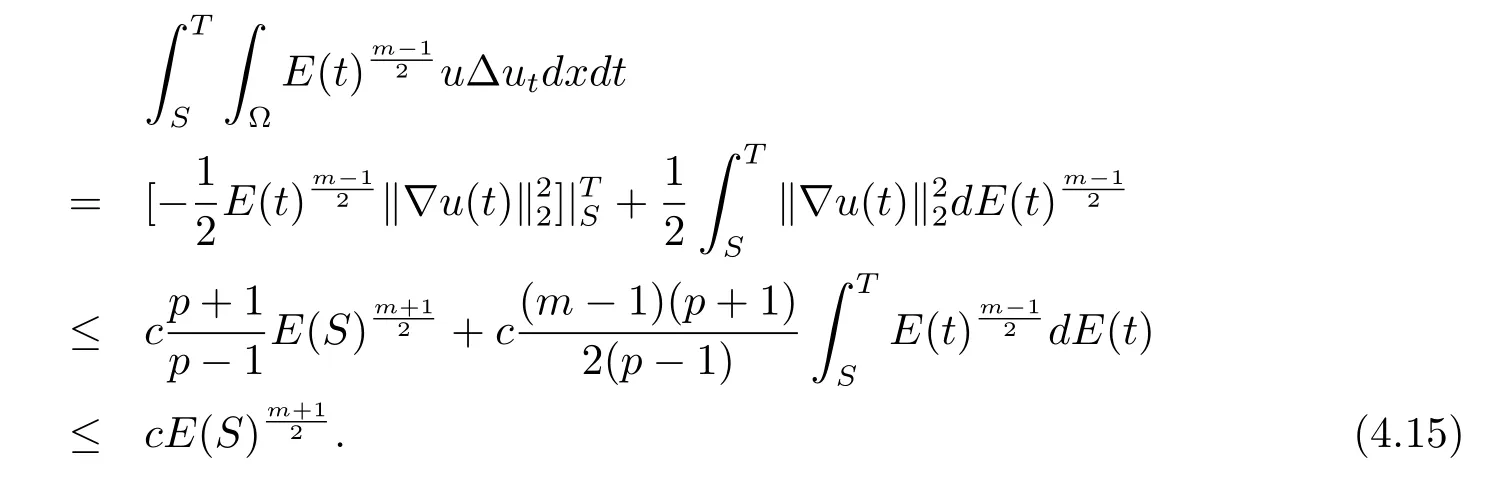
在(4.13),(4.14)式中令ε1,ε2充分小使得

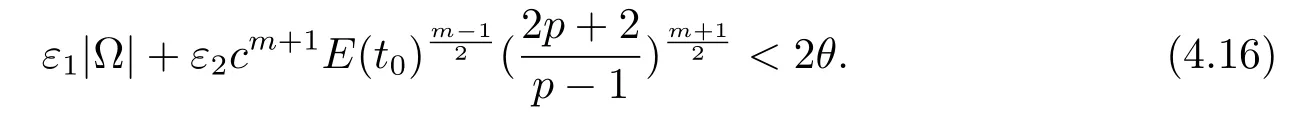
因此由(4.12)-(4.15)式得

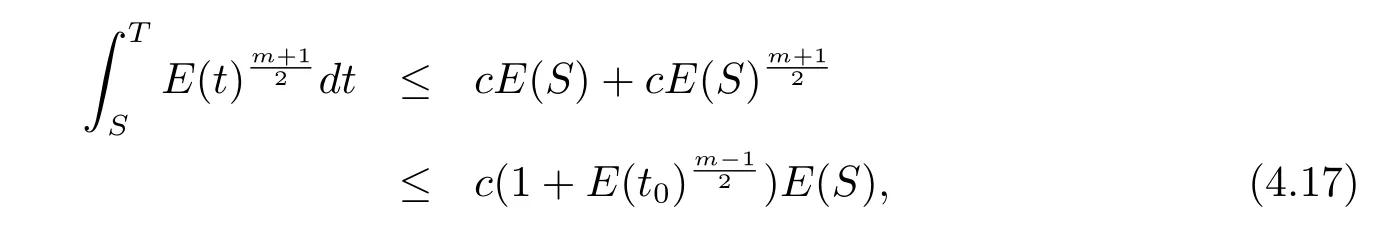
即(4.6)式成立,故由引理4.6得

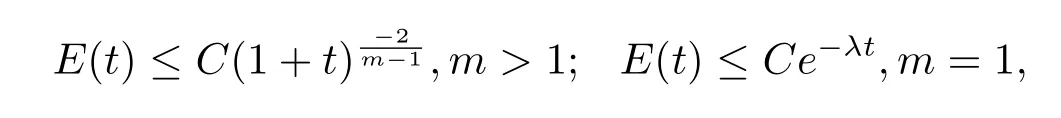
其中C,λ是正常數,t∈[t0,∞),且C依賴于E(t0).

注在定理4.1中并沒有限制m,p的大小關系,給出了整體解的存在性.下面將給出當m≥p時,定理2.1中給出的局部解也是整體存在的.

證考慮通常的能量函數

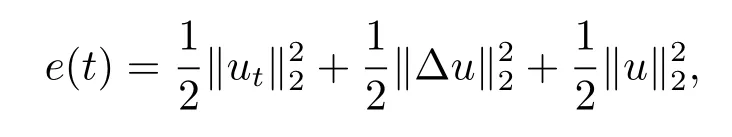
僅利用e(t)很難估計強阻尼項、非線性阻尼項和源項對整體解的影響,為此引進修正的能量函數

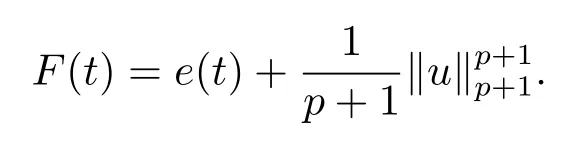
由能量等式知

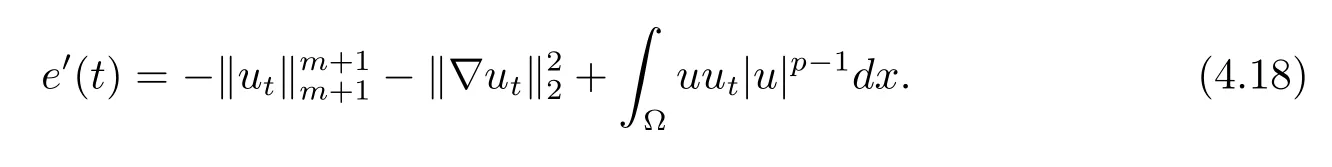
故

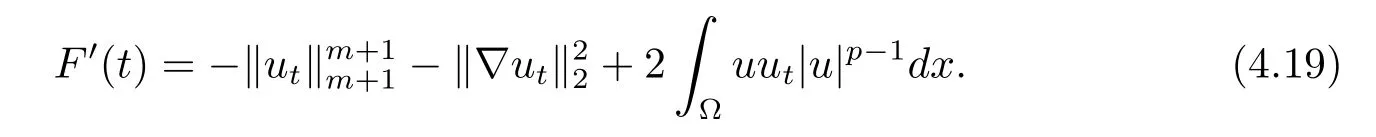
由Young不等式和m≥p可知

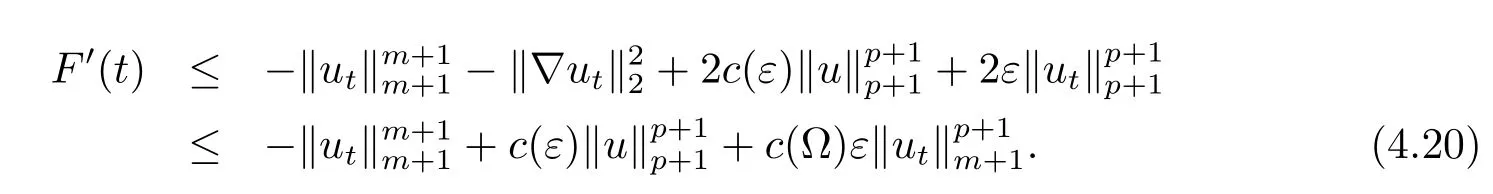
這里討論兩種情況:當‖ut‖m+1＞1時,選取ε充分小使得

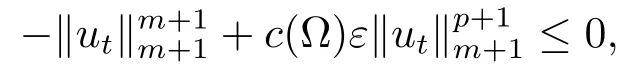
故F＇(t)≤c(ε)‖u‖.當‖ut‖m+1≤1時,可得F＇(t)≤εc(Ω)+c(ε)‖u‖.因此

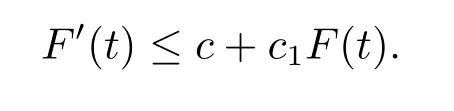
故

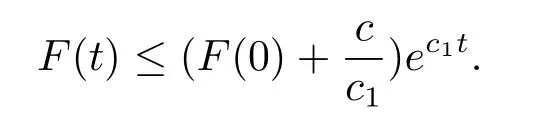
由連續性原理可知定理4.2成立.

[1]Messaoudi S A.Global existense and nonexistence in a system of Petrovsky[J].J.Math.Anal.Appl., 2002,265(2):296-308.

[2]Messaoudi S A.Global existence and decay of solutions to a system of Petrovsky[J].Math.Sci.Res. J.,2002,6(11):534-541.

[3]韓獻軍,薛紅霞.一類具有非線性阻尼和源項的Petrovsky方程整體解的存在性和漸進性[J].高校應用數學學報(A輯),2008,23(2):153-158.

[4]尹麗,韓獻軍,薛紅霞.一類具有非線性阻尼和源項的Petrovsky方程的初邊值問題解的爆破[J].數學實踐與認識,2010,40(4):168-174.

[5]Chen Wenying,Zhou Yong.Global nonexistence for a semilinear Petrovsky equation[J].Nonl.Anal., 2009,70(9):3230-3208.

[6]Chen Hua,Liu GongWei.Global existence,uniform decay and exponential growth for a class of semilinear wave equation with strong damping[J].Acta Math.Sci.,2013,33B(1):41-58.

[7]Lions J L.Quelques methods de resolution des problemes aux limits nonlineaires[M].Paris:Dunod, 1969.

[8]Komornik V.Exact controllability and stabilization.The multiplier method[M].Pairs:Mason John Wiley,1994.

[9]Sattinger D H.On global solution of nonlinear hyperbolic equations[J].Arch.Rat.Mech.Anal., 1968,30(2):148-172.

2010 MR Subject Classification:35L75;35B44

FINITE TIME BLOW UP AND DECAY ESTIMATES OF SOLUTION FOR A CLASS OF FOURTH ORDER NONLINEAR WAVE EQUATION

LI Ning,LEI Qian,YANG Han
(School of Mathematics,Southwest Jiaotong University,Chengdu 611756,China)

In this paper,we consider the fourth order wave equation with nonlinear damping and source term.We prove the existence of a local weak solution and show that this solution blow up in finite time if m＜p and the energy is negative.Furthermore,we discuss,for the evolution of solution enters into the stable set,the solution is global as well as a decay result regardless of any relations between m and p.At last we also show that the solution is global if m≥p,which extends and improves the results in[1-6].

strong damping;forth order wave equation;potential wells;blow-up;decay estimate

MR(2010)主題分類號:35L75;35B44O175.29

A

0255-7797(2016)06-1299-16

?2014-06-11接收日期:2014-09-22

李寧(1990-),女,河南鹿邑,碩士,主要研究方向:偏微分方程.