微波負載電熱耦合的無源互調分析

江 潔,李團結,梅宇健,王鴻鈞

(1.紅河學院工學院,云南蒙自 661100; 2.西安電子科技大學機電工程學院,陜西西安 710071)

微波負載電熱耦合的無源互調分析

江 潔1,2,李團結2,梅宇健2,王鴻鈞1

(1.紅河學院工學院,云南蒙自 661100; 2.西安電子科技大學機電工程學院,陜西西安 710071)

微波負載可改善電路的匹配性能,吸收微波能量.消耗微波能量產生的焦耳熱對微波負載的電阻率產生影響,從而產生無源互調.針對熱場與電磁場耦合時導致時間尺度上的差異引起的微波負載無源互調問題,首先利用分數階微分方法建立了微波負載分數階熱傳導模型;然后建立分數階熱傳導的電路模型;最后結合熱阻效應,推導出微波負載電熱耦合引起的無源互調功率電平表達式.分析了材料的電阻溫度系數、熱阻、熱容對無源互調的影響,為微波負載降低電熱耦合引起的無源互調提供了參考.

微波負載;無源互調;互調失真;分數階微分;電熱耦合;熱阻

無源互調是由無源部件的固有非線性引起的.當電流通過非線性部件時,非線性的電壓-電流特性會導致一個單頻傳輸系統中出現諧波信號傳輸,雙頻或多頻傳輸系統中出現諧波信號及其他不希望有的交調信號頻譜.產生無源互調的原因眾多,例如,金屬-氧化物-金屬接觸、金屬-金屬接觸、磁滯材料的非線性特性和接觸處的接觸污染等[1-4].通常情況下,因為熱變化和電磁波的頻率相差很大,在時間尺度上相差了幾個量級,使得電熱耦合引起的無源互調被嚴重忽視.但是,當輸入多載波的頻率比較接近時,會有功率信號頻率落入材料的熱帶寬中,從而產生電熱耦合過程,使得元件的電阻率隨時間變化,呈現非線性的電壓-電流關系,最終導致無源互調的產生[5-6].

當輸入載波流經微波負載時,微波負載吸收微波能量,產生焦耳熱效應,導致金屬材料電阻率發生時變,電阻率的變化又會影響焦耳熱效應,形成電熱耦合現象.

分數階微分能簡潔、準確描述具有歷史記憶性和空間全域相關性等物理過程,而且分數階導數建模簡單、參數物理意義清楚、描述準確,是復雜物理過程數學建模的重要工具之一[7-8].在微波負載的電熱耦合過程中,熱傳導過程具有明顯的記憶性和遺傳性.相較于熱傳導方程的經驗表達式指數函數[9],應用分數階微分方法能簡潔地表達熱傳導過程,將簡化電熱耦合模型的無源互調(Passive Inter Modulation,PIM)計算.

筆者研究了微波負載電熱耦合產生的PIM問題,首先,用分數階微分簡化熱傳導方程,得到分數階熱傳導方程.再根據分數階熱傳導方程,建立分數階熱傳導電路模型,推導熱傳導結果.最后,結合熱阻效應、耦合電場和熱場,推導出由微波負載電熱耦合產生各階PIM的表達式.對微波終端負載進行仿真,分析電阻溫度系數、熱阻和熱容對PIM的影響.并提出降低微波負載電熱耦合引起無源互調的方法,為其他微波器件的低PIM設計提供理論依據和參考方法.

1　熱傳導和電熱耦合模型

無源器件自熱將導致電阻率變化.研究證明,在多載波下,輸入的功率信號會出現新的頻譜分離,若有功率信號頻譜分量落入熱帶寬時,會產生電熱耦合,使無源器件的電阻率發生時變,產生PIM.其中輸入載波的頻率差與熱變化頻率接近,將產生電熱耦合和PIM;而輸入載波的頻率和比熱變化頻率高很多時,將不產生電熱耦合效應[10].文中研究在雙載波情況下,載波的頻率差功率信號對微波負載電熱耦合PIM的影響.

1.1電熱耦合模型

根據熱電阻效應[11-12]和熱傳導理論,推導得出電熱耦合方程為

其中,T是溫度,單位為K;Rth是熱阻,單位為K·W-1;Cv是熱容,單位為J·K-1·kg-1;J是電流密度,單位為A·m-2;ρe0是電阻率,是常數;α和β是電阻溫度系數.實際上,對于大多數金屬,熱電阻表達式中的一階系數比二階及以上系數要大好幾個量級,故一階系數是產生非線性的主要原因.

1.2熱傳導模型

熱傳導方程描述在一個實體中,熱能會從高溫區域流向低溫區域的一個現象.通過分析半無窮大矩形結構的熱傳導方程,可得到該結構的熱擴散特性.一個半無窮大矩形結構的熱傳導方程為

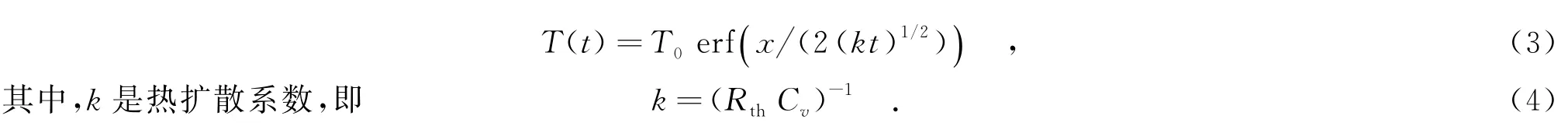
假設在x=-∞處的溫度是零度,在x=0處的溫度是T0,溫度響應會有一個含有誤差函數的解析解,其表達式[13]為

該解析解能較好地描述熱過程,但由于含有誤差函數,而且熱響應表達式中的空間和時間變量沒有分離,若直接進行電熱耦合的PIM分析,計算過程則會很復雜.

熱響應特征還可描述為如下多階的指數型函數[9,14]:

其中,τi是時間常量,τi=RiCi;Ri和Ci是熱阻和熱容.該高階熱響應表達式,不僅使電熱耦合模型復雜,而且在實際應用中,該表達式的熱阻、熱容值不能簡單計算,因此,不適于分析電熱耦合的PIM問題.

1.3分數階熱傳導模型

分數階微分的定義主要有3種形式,包括Grunwald-Letnikov定義、Riemann-Liouville定義和Caputo定義,其中,Caputo定義的分數階微分所描述問題的初始條件與整數階微分方程的初始條件是一致的,因而能解釋相關現象,適合實際工程中的建模計算問題.引入分數階微分方法,將精確、簡潔的對熱傳導過程建模,簡化溫度場的計算,為更好地分析電熱耦合的PIM問題奠定了基礎.

Caputo定義的分數階微分如下[7]:

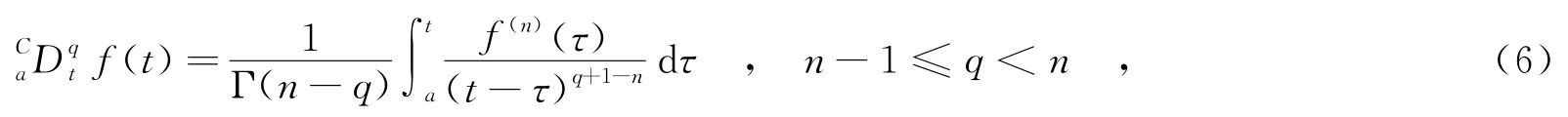
其中,C是Caputo分數階微分算子;a是積分下限;q是導數的階數;t是時間變量;Γ是gamma函數,為確定積分區域;變量τ→t.

分數階微分的拉普拉斯變化及其逆變換為

從而構造了分數階熱傳導模型,簡化了電熱耦合PIM問題的分析.

1.4微波負載電熱耦合分析

圖1所示電阻是常用的一種微波負載,電阻元件上邊界是隔離層,下邊界與熱傳導介質相連,熱傳導介質裝配在一個散熱器上.當電阻元件被劃分為無窮小的單元時,因為熱傳導介質的尺寸遠大于每個電阻單元,所以可將每個電阻單元的熱傳導過程簡單處理為一維的熱傳導,用一維熱傳導方程表示.考慮到熱擴散的速率,可認為同一時刻每個電阻單元的溫度場是一致的,因此,電阻單元間是串聯的,每個無窮小單元的熱效應可等效為一個集總元件電阻的熱效應.利用分數階微分,將該電阻元件的一維熱傳導方程推導為分數階熱傳導模型.

圖1　電阻元件示意圖

根據圖1所示的熱系統,給出如下邊界條件:

其中,TH(t)是電阻元件的表面穩態溫度,其表達式為

環境溫度可直接線性疊加到上面的解.為簡化計算,假設外界溫度為零度.因為一維熱傳導方程是基于時間和空間變量建立的,首先通過拉普拉斯變換分離時間和空間變量.

對式(2)進行拉普拉斯變化,可得到

其中,x是空間位置,s是拉式變量.由于邊界條件是在位置x=0和x=-∞處的溫度為零度,式(11)的解為

由于式(13)中存在s-1/2,因此,可用Caputo定義分數階微分和分數階微分的拉式變換進行簡化.整理得

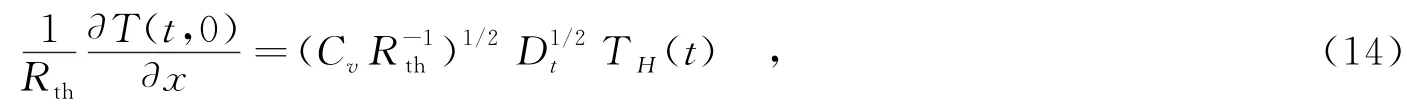
即電阻元件表面(x=0)溫度的分數階形式.式(14)的解,即是電阻表面的熱響應表達式.

通過拉普拉斯變換分離了空間和時間變量,結合分數階微分得到電阻表面的熱響應方程,而不用求解整個空間的溫度場.同時解決了熱變化和電磁波時間尺度上不同所帶來的計算量膨脹的問題[10],在實際應用中具有重要的意義.通過分數階微分建立的分數階熱傳導方程,簡化了熱傳導的計算,為分數階電熱耦合電路模型和電熱耦合PIM表達式的推導奠定了基礎.

2　分數階熱傳導方程的電路模型及PIM推導

2.1分數階熱傳導方程的電路模型

分數階熱傳導方程的解通常分為解析解和數值解.由于引入了分數階微分,使得熱傳導方程的解析解非常復雜[13],不適合進一步分析微波負載的電熱耦合PIM問題.而用數值方法計算,雖然邊界元、有限元、有限差分等方法可精確計算出熱場,但是計算量很大,影響計算效率.為此,文中根據分數階熱傳導方程,以電路為基礎,構造描述熱傳導特性的電路模型,計算簡單高效.

熱響應表達式與串聯的低通濾波器一致.RC電路是基本的低通濾波器,用電路來仿真熱響應過程.相對于傳統的RC低通濾波電路,根據分數階熱傳導方程,分數階電路模型如圖2所示,表示電阻元件的熱響應特征.圖2中的電容根據微波負載的熱容和熱阻重新定義為(jωCth)1/2,其中,ω為雙載波的頻差,Cth的表達式如下:

圖2中的激勵源Q來自于負載自熱消耗的電功率Pdis,外界溫度Ta作為一個電壓源加載到等效電路模型中.若一個階躍功率信號作為等效電路的激勵源時,該電路的階躍響應具有與一個實體某位置處溫度與時間的曲線相同的“長尾記憶”效應,故該等效電路可以表征熱傳導特征.

圖2　分數階熱傳導方程的電路模型

2.2電熱耦合PIM表達式推導

根據上面的分數階熱傳導方程和熱阻效應,可重新定義電熱耦合方程,并以此推導出PIM表達式.器件的熱阻效應[10]耦合了電場和熱場,由于α?β,故用線性表達式來描述熱阻:

其中,R0是熱阻在273 K溫度下測得的參考電阻,Ta是外界溫度,α是一階熱電系數.瞬態溫度可定義為

其中,等效熱阻是分數階簡化模型的頻域等效電阻,表達式為

微波負載產生的熱量,可定義為

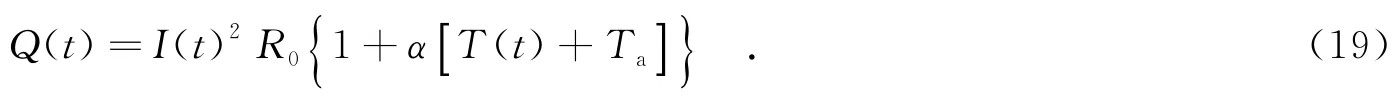
電壓和電流的關系服從歐姆定律,即

考慮到溫度是由產生的熱量決定的,而產生的熱量又是由通過的電流和電阻決定的,可得溫度的頻域表達式為

頻域下的電流、電壓、熱量、溫度和等效熱阻在式(17)～(21)中被定義.將這幾個表達式代入歐姆定律中,可得到一個遞推公式為

因此,得到電熱PIM表達式為

其中,R是當前溫度下的電阻.

電熱耦合的PIM表達式包括了材料和環境溫度參數、輸入信號頻率和功率,已知輸入信號參數和微波負載材料的電阻溫度系數、熱阻和熱容,就可計算得到微波負載電熱耦合產生的PIM.該表達式可方便簡單計算出微波負載電熱耦合引起的PIM,為微波負載的材料選擇提供了理論依據,以此降低微波負載電熱耦合引起的PIM,從而保證整個通信系統低PIM的需求.

3　實例仿真

在微波系統中,微波電阻是很常用的有損實驗元件來匹配端口阻抗的.大功率信號通過微波電阻會產生熱量,產生的熱量會使微波電阻的阻值發生變化,從而產生PIM.分析電熱耦合需要知道材料的電阻溫度系數、熱容和熱阻.

當輸入信號為20 W雙載波時,用輸入頻率差為1～1000 Hz的載波掃頻微波終端,根據上面建立的電熱耦合PIM表達式來計算電熱非線性引起的PIM.

(1)當Rth和Cth一定,電阻溫度系數分別是α1=3.8×10-3/℃和α2=1.6×10-6/℃時,計算三階PIM,如圖3所示.

圖3　不同溫度系數得到的三階PIM

(2)當電阻溫度系數α和Cth一定,熱阻分別是Rth1=30 K·W-1和Rth2=200 K·W-1時,計算三階PIM,如圖4所示.

圖4　不同熱阻得到的三階PIM

(3)當電阻溫度系數α和Rth一定,熱容分別是Cth1=0.022 J·K-1和Cth2=7×10-5J·K-1時,計算三階PIM,如圖5所示.

圖5　不同熱容得到的三階PIM

由圖3～5可以看出:①隨著雙載波頻率差的增大,PIM會隨之下降,雙載波頻率越接近,電熱耦合程度越強,PIM越大;②電阻溫度系數對PIM影響很大,電阻溫度系數越大,PIM越大;③熱阻大小對PIM影響相對較小,對于PIM的影響基本可以忽略;④熱容對PIM影響較大,熱容越大,PIM越小.綜合以上分析可得,設計器件時盡量選擇電阻溫度系數小的材料,合理增大無源器件的尺寸,增大熱容,這樣將降低PIM影響.

4　結束語

當輸入多載波的頻率比較接近時,會有功率信號頻率落入材料的熱帶寬中,產生電熱耦合過程,使得微波負載的電阻率隨時間變化,呈現非線性的電壓-電流關系,導致電熱耦合PIM的產生.筆者針對微波負載電熱耦合產生PIM問題,利用分數階微分降階具有“長尾效應”的熱傳導方程,結合分數階熱傳導電路模型,用等效電路來表征微波負載熱傳導特征,簡化分數階熱傳導方程的數值計算,得出以下結論:雙載波頻率差增大,PIM值下降,雙載波頻率差越小,PIM越大;電阻溫度系數越大,PIM越大;熱阻基本不影響PIM值;熱容越大,PIM越小.仿真結果證明了分析方法的有效性.

[1]JIANG J,LI T J,MA X F,et al.A Nonlinear Equivalent Circuit Method for Analysis of Passive Intermodulation of Mesh Reflectors[J].Chinese Journal of Aeronautics,2014,27(4):924-929.

[2]KOZLOV D S,SHITVOV A P,SCHUCHINSKY A G.Characterisation of Passive Intermodulation in Passive RF Devices with X-parameters[C]//2014 Loughborough Antennas and Propagation Conference.Piscataway:IEEE,2014: 64-67.

[3]BOYHAN J W,HENZING H F,KODURU C.Satellite Passive Intermodulation:Systems Considerations[J].IEEE Transactions on Aerospace and Electronic Systems,1996,32(3):1058-1064.

[4]JIANG J,LI T J,MA X F,et al.A Nonlinear Equivalent Circuit Method for Analysis of Passive Intermodulation of Mesh Reflectors[J].Chinese Journal of Aeronautics,2014,27(4):924-929.

[5]ISHIBASHI D,KUGA N.Analysis of 3rd-order Passive Intermodulation Generated from Metallic Materials[C]// Proceedings of 2008 Asia-Pacific Microwave Conference.Piscataway:IEEE,2008:4958017.

[6]WILCOX J Z,MOLMUD P.Thermal Heating Contribution to Intermodulation Fields in Coaxial Waveguides[J].IEEE Transactions on Communications,1976,24(2):238-243.

[7]OLDHAM K B,SPANIER J.The Fractional Calculus:Theory and Applications of Differentiation and Integration to Arbitrary Order[M].New York:Dover Publications,2006:10-58.

[8]HILFER R.Applications of Fractional Calculus in Physics[M].Singapore:World Scientific,2000:1021-1032.

[9]BECHTOLD T,RUDNYI E,KORVINK J.Dynamic Electro-thermal Simulation of Microsystems—a Review[J]. Journal of Micromechanics and Microengineering,2005,15(11):17-31.

[10]WILKERSON J R.Passive Intermodulation Distortion in Radio Frequency Communication Systems[D].Releigh:North Carolina State University,2010.

[11]MEADEN G T.Electrical Resistance of Metals[M].New York:Plenum Press,1965:59-141.

[12]葉鳴,賀永寧,崔萬照.基于電熱耦合效應的微帶線無源互調機理研究[J].電波科學學報,2013,28(2):220-225. YE Ming,HE Yongning,CUI Wanzhao.Passive Intermodulation Mechanism of Microstrip Lines Based on the Electrothermal Coupling Effect[J].Chinese Journal of Radio Science,2013,28(2):220-225.

[13]KHOLPANOV L P,ZAKIEV S E.Fractional Integro-differential Analysis of Heat and Mass Transfer[J].Journal of Engineering Physics and Thermophysics,2004,78(1):33-46.

[14]任興榮,柴常春,馬振洋,等.電磁脈沖作用下二極管二次擊穿電熱特性[J].西安電子科技大學學報,2013,40(2): 36-42. REN Xingrong,CHAI Changchun,MA Zhenyang,et al.Electrothermal Characteristics of Second Breakdown in Diodes under the EMP Stress[J].Journal of Xidian University,2013,40(2):36-42.

(編輯:齊淑娟)

簡 訊

我校兩項成果獲2015年度國家科技二等獎.其中,“雷達目標分類技術”,發明了目標分類新方法,解決了目標分類重大技術難題,提升了我國現有裝備的信息獲取能力.“氮化鎵基紫外與深紫外LED關鍵技術”,提出創新的表面增強脈沖反應生長方法、脈沖超晶格p型摻雜方法和納米微腔器件結構,解決了材料生長、摻雜和紫外光提取效率等重大難題,獲得中國和美國發明專利授權22項,在信息產業、裝備制造、國家安全、醫療健康等領域具有廣泛應用前景.

摘自《西電科大報》2016.1.22

Passive intermodulation analysis of coupled electro-thermal microwave loads

JIANG Jie1,2,LI Tuanjie2,MEI Yujian2,WANG Hongjun1
(1.Engineering College,Honghe Univ.,Mengzi 661100,China; 2.School of Mechano-electronic Engineering,Xidian Univ.,Xi’an 710071,China)

Microwave loads are used to improve the matching performance of circuits and absorb the microwave energy.The microwave loads generate the joule heat to affect the electrical resistivity after consuming microwave energy which may produce the passive intermodulation(PIM).Electro-thermal compling leads to the difference of the time scale which produces PIM.In order to address the problem,the fractional heat conduction model of microwave loads is created by the fractional calculus firstly.Then the circuit model of the fractional heat conduction is established.Eventually,the thermal resistance effect is considered.The expression for the PIM power level caused by the coupled electro-thermal microwave loads is derived.The influences of the material’s temperature coefficient of resistance,thermal resistance and thermal capacity to PIM are revealed,which provides the fundamental basis for reducing the PIM from the coupled electro-thermal microwave loads.

microwave load;passive intermodulation;intermodulation distortion;fractional calculus; thermal-electric coupling;thermal resistance

TN972

A

1001-2400(2016)03-0179-06

10.3969/j.issn.1001-2400.2016.03.031

2015-10-20

國家自然科學基金資助項目(51375360);紅河學院科研資助項目(XJ15Y20)

江 潔(1981-),女,講師,西安電子科技大學博士研究生,E-mail:jiang123456jie@126.com.

王鴻鈞(1965-),男,教授,E-mail:wanghj302@163.com.